參考系波動下的參考系無關測量設備無關量子密鑰分發協議*

谷文苑 趙尚弘 東晨 王星宇 楊鼎

1) (空軍工程大學信息與導航學院, 西安 710077)

2) (密碼科學技術國家重點實驗室, 北京 100878)

3) (國防科技大學信息與通信學院, 西安 710006)

參考系無關測量設備無關量子密鑰分發協議是解決實際系統中參考系對準問題的有效途徑, 但其安全性的前提是參考系偏移速度緩慢.考慮到現實參考系波動和信號長度有限的情況, 重點討論了參考系偏移和波動下的有偏基參考系無關測量設備無關量子密鑰分發協議性能的有效性.仿真結果表明協議密鑰率是關于偏移角的周期函數, 同時也是波動角的遞減函數, 為下一步參考系無關測量設備無關量子密鑰分發協議實用化打下了理論基礎.

1 引 言

量子密鑰分發 (quantum key distribution,QKD)是基于量子力學及基本定理的一種新型密鑰體系[1,2], 以其絕對的安全性得到了廣泛的研究,在理論研究和實驗驗證方面進展迅速[3-9].但現實設備和實驗條件總是會與理想模型及假設存在一定差距, 這導致實際的QKD系統仍然存在許多安全性問題[10-16].2012年Lo等[17]提出了測量設備無關量子密鑰分發 (measurement device independent quantum key distribution, MDI-QKD)協議, 在克服探測端全部安全漏洞的同時實現了協議性能的提升.近幾年, 基于相位、偏振等編碼方式的MDI-QKD演示實驗已經相繼完成[18-20].然而, 無論采用何種編碼方式, 通信雙方都需確立共享參考系以保證MDI-QKD系統有效的Bell測量, 但同時多參考系之間的校準會增加MDI-QKD系統的復雜性, 甚至可能產生信息泄露, 對系統安全產生威脅.

2014年, Yin等[21]提出了參考系無關測量設備無關量子密鑰分發(reference frame independent measurement device independent quantum key distribution, RFI-MDI-QKD)協議, 有效地解決了參考系校準的問題, 并實現了系統性能在參考系緩慢偏移情況下的穩定性.然而, 已有研究表明統計波動下的RFI-MDI-QKD協議不再具有對參考系偏差的魯棒性, 會隨偏差角的增大產生性能衰減, 但這些分析都只是選取固定的參考系偏差角度進行分析, 并未涉及一般化情況, 且沒有考慮參考系波動的情況[22-26].在實際環境中, 參考系偏差角會在一定范圍內產生波動, 雖然文獻[27, 28]已經討論分析了參考系波動對參考系無關QKD協議 (reference frame independent quantum key distribution, RFI-QKD)的影響, 但仍然缺乏對參考系波動下RFI-MDI-QKD協議的性能分析.

本文主要研究了參考系波動下RFI-MDIQKD協議的性能.考慮到實際參考系波動的問題和有限長效應, 通過公式推導和仿真分析, 得到了參考系偏移角和波動角與有偏基RFI-MDI-QKD協議相關參數間的關系.仿真結果表明, 協議的性能與參考系偏差的角度密切相關, 并且其密鑰率隨參考系偏移角產生周期性波動, 隨參考系波動角的增大而減小.

2 理論與模型

2.1 有偏基RFI-MDI-QKD模型

以偏振編碼為例, 在誘騙態RFI-MDI-QKD協議中, Alice 和 Bob 使用三組共軛基{Z,X,Y}對量子態進行編碼.協議假設Alice和Bob的Z基完全對準, 而兩者的X基和Y基可以存在β角的偏差, Alice和Bob的三組基具體的關系如下[22-26]：

式中βA(B)代表著Alice和Bob的X基和Y基偏離標準參考系的角度.此時,和構成Z基,分別構成X基和Y基.其中Z基主要用于密鑰的產生,X基和Y基的測量結果主要用于估計限制Eve獲取的信息量的參數C.在漸近極限情況下,RFI-MDI-QKD協議具備對參考系偏差的魯棒性,而現實情況下信號脈沖長度總是有限的.

為緩解有限長效應對RFI-MDI-QKD協議的影響, 文獻[29]提出了有偏基RFI-MDI-QKD協議以產生更高的密鑰率.該協議與原始誘騙態RFI-MDI-QKD協議不同點在于：原始誘騙態RFI-MDI-QKD 協議Z,X,Y基編碼的信號態和誘騙態的平均光子數是相同的, 而有偏基RFIMDI-QKD協議的量子態有三種強度, 即信號態μ、誘騙態ν、真空態ω, 其中Z基下Alice和Bob只準備信號態μ,X和Y基下隨機準備信號態μ和誘騙態ν.因此, 有偏基RFI-MDI-QKD協議密鑰率的計算公式為[29]

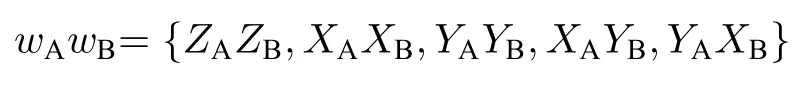
且C值在 0—2 內取值,C值越小,IE越大.參數C與不同編碼基下的增益和誤碼率有關, 這些測量結果滿足[24]

2.2 參考系偏移和波動下的有偏基RFIMDI-QKD模型

如圖1所示, 在實際不穩定的環境中, 由于相對運動和平臺抖動, 通信雙方共享的參考系總是會發生偏移且產生波動, 即Alice和Bob間的參考系方向夾角β不再是一個固定的值, 而是在一定的范圍內變化、波動[27,28], 即 [θ-δ,θ+δ] .

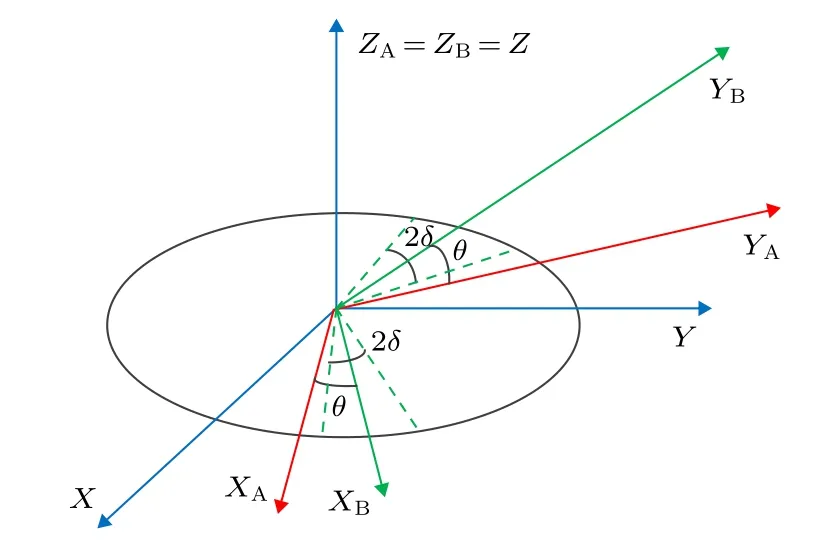
圖1 Alice 和 Bob 的三組共軛基的實際位置關系圖Fig.1.Relationship among reference frames of Alice and Bob.

文獻[27, 28]通過在波動范圍進行積分詳細討論了參考系偏移角和波動角與RFI-QKD協議性能間的關系.本文將此擴展到二維, 采用相同的方法來分析參考系波動下的有偏基RFI-QKD協議的性能.將參考系偏差β=[θ-δ,θ+δ] 代入求積分可得

其中θ為參考系偏移的角度,δ為參考系波動的角度, 假設它們的取值范圍均為 [ 0°,90°] .將(5)式代入(1)—(4)式, 可以求得參考系波動下有偏基RFI-MDI-QKD協議C值和密鑰率R的關系式.

3 仿真與分析

考慮到實際信號脈沖的數量有限的實際情況,根據上述推導的公式可以得到參考系偏移角θ和波動角δ與有偏基RFI-MDI-QKD協議的參數C和密鑰率R的關系.為方便比較, 固定協議的傳輸距離為20 km, 并假設切爾諾夫界失敗的概率為ε=10-10, 脈沖總數為N=3×1012, 糾錯 (隱私放大)失敗的概率為表1列出了該協議其他的仿真參數[24-26].

表1 有偏基 RFI-MDI-QKD 協議的主要仿真參數Table 1.List of parameters of RFI-MDI-QKD with biased bases in the simulation.

圖2顯示了參考系偏移和波動下有偏基RFIMDI-QKD協議的C值變化.由圖2(a)可知：當固定波動角δ時,C值為偏移角θ的最小周期為 π /2 的函 數, 而 且 在 [ 0°,90°] 范 圍 內 存 在C(π/4+θ)=C(π/4-θ); 當改變波動角δ時,C值隨波動角δ增大而減小.圖2(b)則顯示了有偏基誘騙態RFIMDI-QKD協議C值與波動角δ的關系.當固定偏移角θ時,C值與圖2(a)曲線趨勢相同, 這說明波動角δ越大, 竊聽者可能竊取的信息IE就越多; 當改變偏移角θ時, 可以注意到曲線θ=40°與曲線θ=70°完全重合, 這是因為C值是關于偏移角θ的對稱軸為 π /4 的周期函數.

圖3為有偏基RFI-MDI-QKD協議密鑰率R與偏移角θ、波動角δ的三維關系圖.由圖3可知, 該協議的密鑰率R會隨偏移角θ、波動角δ變化而發生變化.其中, 密鑰率R隨偏移角θ呈周期性變化, 并且變化范圍較小, 而波動角δ對密鑰率R的影響較大.圖4(a)和圖4(b)分別是有偏基RFI-MDI-QKD協議密鑰率R與偏移角θ、波動角δ的關系圖.由圖4可知, 由于密鑰率R與描述竊聽者獲取的信息IE的參數C有關,R隨偏移角θ、波動角δ變化的趨勢與參數C相同, 即密鑰率R是關于偏移角θ的周期為 π /2 且對稱軸為 π /4 的函數, 同時也是波動角δ的遞減函數.可以注意到當偏移角θ接近 2 2.5°(67.5°) 時,R會隨波動角δ的增大而產生驟減, 這是因為 2 2.5°(67.5°) 對應于密鑰率R關于偏移角θ的函數谷值, 所以當δ較大時,協議性能會迅速下降.

圖2 參考系偏移和波動下有偏基 RFI-MDI-QKD 協議的 C 值 (a) 參數 C 與偏移角 θ 的關系圖; (b) 參數 C 與波動角 δ 的關系圖Fig.2.Parameter C of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation：(a) The parameter C vs.the reference frame deviation θ ; (b) the parameter C vs.the reference frame fluctuation δ .

圖3 有偏基 RFI-MDI-QKD 協議密鑰率 R 與偏移角 、波動角 δ 的關系圖Fig.3.Secure key rates R of RFI-MDI-QKD with biased bases in regard to the reference frame deviation θ and fluctuation δ .

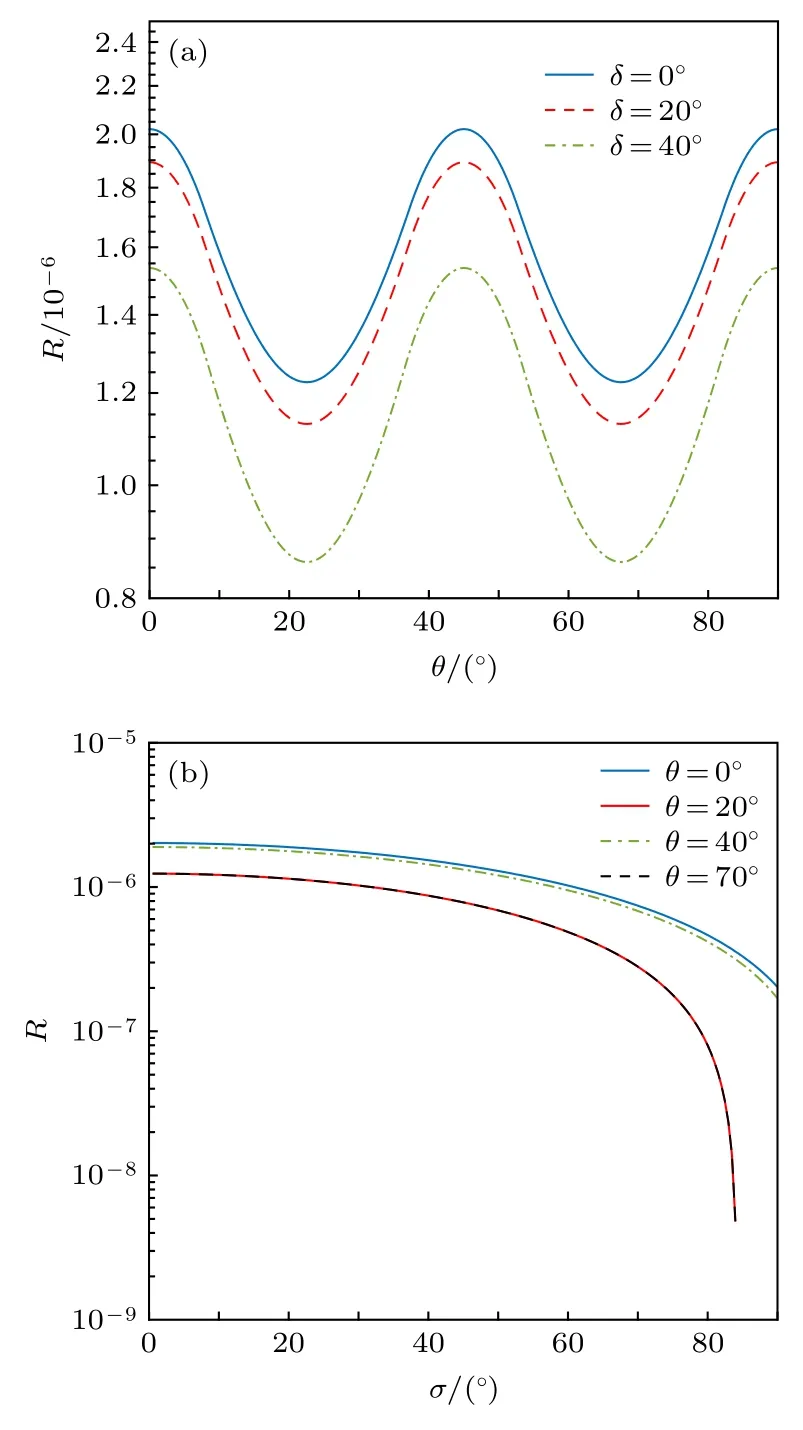
圖4 參考系偏移和波動下有偏基RFI-MDI-QKD協議密鑰率變化圖 (a) 密鑰率 R 與偏移角 θ 的關系圖; (b) 協議密鑰率R與波動角 δ 的關系圖Fig.4.Secure key rates of RFI-MDI-QKD with biased bases under reference frame deviation and fluctuation：(a) The secure key rates R vs.the reference frame deviation θ ;(b) the secure key rates R vs.the reference frame fluctuation δ .

4 結 論

為解決MDI-QKD系統參考系需校準的問題,本文重點研究了有偏基RFI-MDI-QKD協議.針對現實環境中參考系波動的問題并考慮到有限長效應的情況, 分析了參考系偏移和抖動下有偏基RFI-MDI-QKD協議的有效性, 并分別討論了參考系偏移角θ和波動角δ與協議參數C及密鑰率R間的關系.仿真結果表明參數C和密鑰率R均為關于偏移角θ的最小周期為 π /2 且對稱軸為 π/4的函數, 同時也是波動角δ的遞減函數, 為下一步RFI-MDI-QKD協議實用化打下了理論基礎.