多晶石墨烯納米帶熱電性能的理論研究*

許易 許小言 張薇 歐陽滔 2)? 唐超2)?

1) (湘潭大學物理與光電工程學院, 湘潭 411105)

2) (湘潭大學, 微納能源材料與器件湖南省重點實驗室, 湘潭 411105)

熱電材料能夠將廢熱能直接轉換成電能, 近年來受到了科技工作者們的廣泛關注.本文采用非平衡格林函數方法系統地研究了晶界對石墨烯納米帶熱電性能的調控作用.研究結果表明：晶界能有效地提高石墨烯納米帶的塞貝克系數, 同時可以極大地抑制其熱導(包含電子和聲子部分).基于這兩個積極的效應, 多晶石墨烯納米帶的熱電轉換性能得到了顯著的增強.在室溫下, 多晶石墨烯納米帶的熱電品質因子約為0.3, 較完美石墨烯納米帶(約為0.05)提升了6倍左右.并且發現晶界的數量和系統的長度還能進一步提升多晶石墨烯納米帶的熱電性能, 但系統的寬度對其影響有限.這些結果表明, 多晶結構可以顯著提升石墨烯納米帶的熱電轉換效率.這將為設計和制備基于石墨烯納米帶的熱電器件提供新的途徑.

1 引 言

熱電材料作為能將熱能和電能進行相互轉換的一種功能材料, 其應用近年來受到了人們廣泛的關注, 其熱電轉換效率可以采用熱電品質因子ZT=σS2T/k來衡量, 其中S為塞貝克系數,σ為電子電導,k為熱導(包含電子貢獻部分ke和聲子貢獻部分kp).由于電子和聲子輸運之間強烈的耦合性,因此傳統的塊體材料熱電品質因子普遍較為低下[1].然而, 近年來的研究表明, 由于量子限域效應的影響, 低維納米材料顯現出比傳統塊體材料更高的熱電轉換效率[2-6].因此, 尋找具有優異熱電轉換性能的納米材料或改良現有納米材料的熱電性能已成為目前熱電研究領域的一大熱點.

自從2004年發現石墨烯以來, 石墨烯及其衍生納米結構引起了人們廣泛的興趣.因為石墨烯具有獨特的幾何結構, 其納米結構具有許多優異的物理屬性[7-9].例如：良好的機械力學性能[10]、較高的熱穩定性[11], 以及出色的光學特性[7,12].更為有趣的是, 石墨烯具有超高的載流子遷移率, 其在室溫下可達 200000 cm2/(V·s)[13].Dragoma 等[14]發現石墨烯的塞貝克系數高達30 mV/K, 是目前已知材料中最高的.這預示著石墨烯將有可能成為一種理想的熱電材料.然而, 研究發現石墨烯的熱導高達 3000 W/mK (懸浮樣品)[15,16], 這極大地限制了其在熱電領域的廣泛應用.近年來, 人們提出了多種方法來有效地減低石墨烯的熱導進而提高其熱電品質因子, 例如：超晶格[17]、缺陷工程[18,19]、摻雜[20,21].這些手段均能在一定程度上增強石墨烯的熱電轉換性能, 同時也有效地推動了對石墨烯熱電性質研究的發展.不過, 值得注意的是, 實驗合成和制備的石墨烯, 由于其生長基底和石墨烯成核晶向的差異性, 往往更容易形成多晶結構[22,23].事實上, 多晶結構是調控材料物理性質的有效途徑之一[24-26].先前的分子動力學模擬研究也表明, 多晶石墨烯中的晶界能對聲子產生極大的散射效果, 進而極大地降低其熱輸運性能[27].然而, 迄今為止鮮有研究工作關注到晶界對石墨烯及其衍生納米結構電子輸運性質尤其是熱電性質的影響.

本文采用非平衡格林函數方法[28,29]系統地探索了晶界對石墨烯納米帶熱電性能的調控作用.研究結果表明, 晶界能有效地增強石墨烯納米帶的熱電轉換效率.在室溫下, 晶界的存在可將完美石墨烯納米帶的熱電品質因子提高6倍(從0.05提升至0.3).這主要歸因于晶界提高了石墨烯納米帶的塞貝克系數以及有效地抑制了其熱導(包含電子和聲子部分).還討論了尺寸效應對多晶石墨烯納米帶熱電性能的影響.發現多晶石墨烯納米帶的熱電品質因子會隨著長度的增加而上升, 隨著寬度的增加而逐漸下降.這些結果表明, 多晶結構可以顯著提升石墨烯納米帶的熱電轉換效率.這將為設計和制備基于石墨烯納米帶的熱電器件提供新的途徑.

2 模型和方法

圖1展示的是多晶石墨烯納米帶原子結構模型.整個結構可以分成3個不同的區域：由完美鋸齒型石墨烯納米帶構成的左右電(熱)極, 以及由多個不同晶向石墨烯片組成的中心區.這里多晶石墨烯納米帶晶界的數量用N來表示, 中心區的長度和寬度分別用L和W來表示.

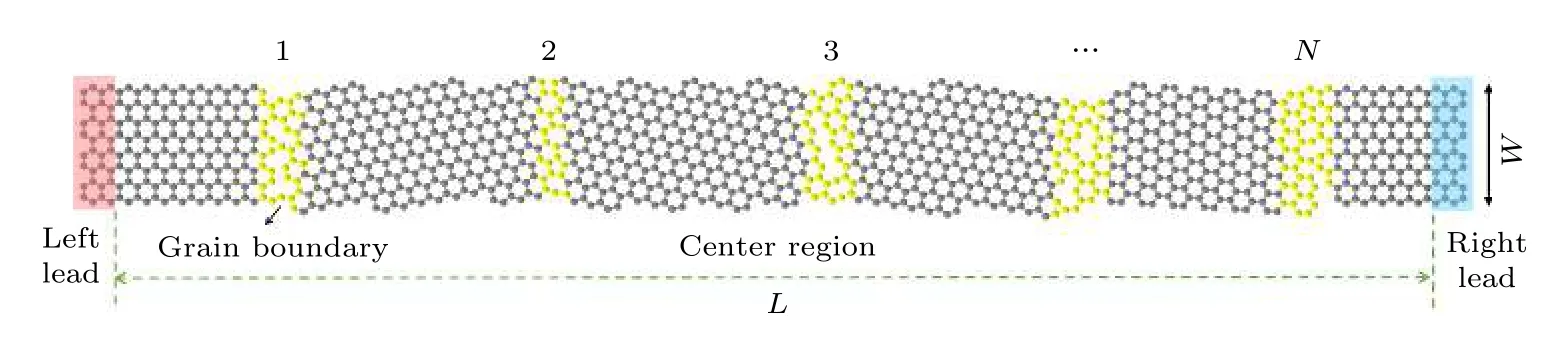
圖1 多晶石墨烯納米帶原子結構模型示意圖Fig.1.Schematic diagram of polycrystalline graphene nanoribbons.

采用非平衡格林函數方法來計算系統的電子和聲子輸運性質[28,29].需要指出的是, 由于石墨烯中電聲耦合較弱以及較長的電子和聲子平均自由程, 因此在計算過程中忽略了電聲耦合效應, 并認為電子和聲子是獨立進行輸運的.先前有關石墨烯熱電性能的研究均采用類似的處理方法[30,31].對于多晶石墨烯納米帶的電子輸運性質部分, 采用緊束縛模型來構造其哈密頓量[32], 該哈密頓量可以表示為

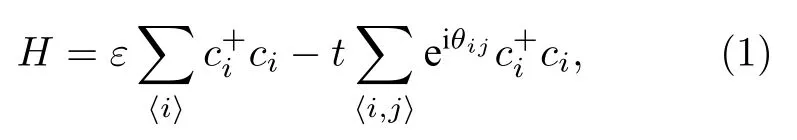
其中ε為格點能并設為0;t為躍遷能, 其值具有距離依賴關系,t=t0exp[-3.37(l/a-1)][33], 其中t0是石墨烯的原始躍遷能,l和a(1.42 ?)分別為碳原子之間的距離和原始石墨烯中最近鄰石墨烯的C—C鍵長.基于(1)式所給出的緊束縛哈密頓量, 電子的推遲格林函數可以寫為

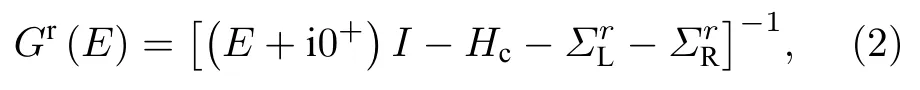
其中E為電子能量;代表半無限長左(右)電極的自能, 其可以通過快速迭代方法進行求解.基于超前格林函數Ga(E)=Gr(E)?和自能可以計算并獲得系統的電子透射系數Te(E)[32]：

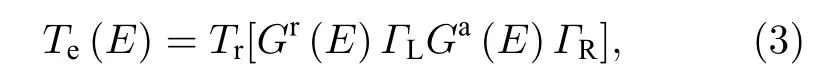
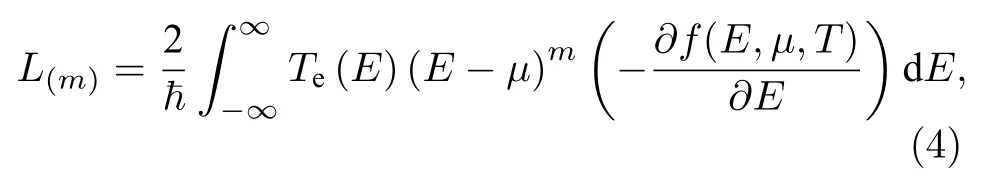
其中f(E,μ,T) 為費米-狄拉克分布函數,μ是化學勢,E是入射電子的能量,T是溫度.σ,S和ke可以用以下公式計算：

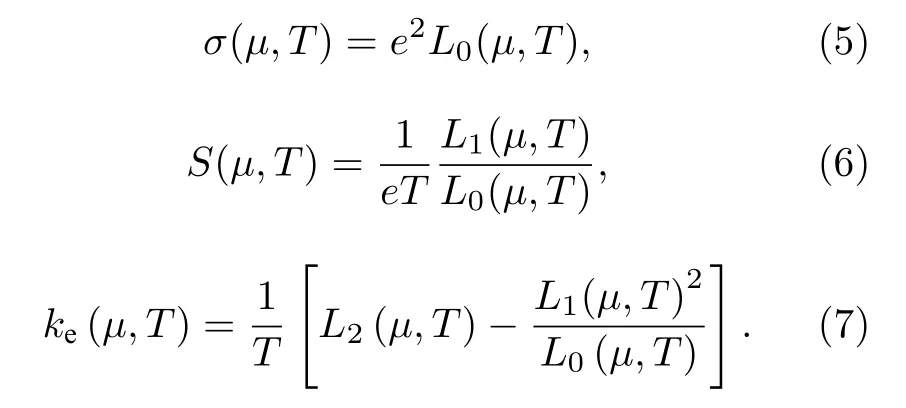
與電子推遲格林函數類似, 聲子推遲格林函數可以表示為

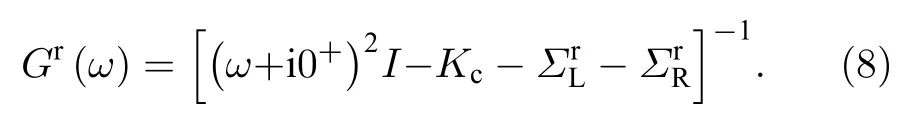
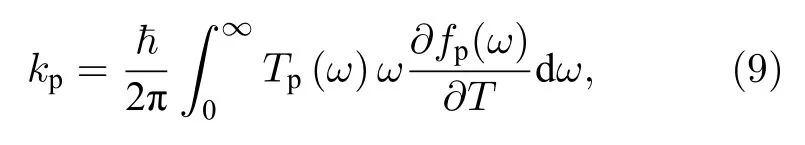
其中fp(ω)為玻色-愛因斯坦分布函數.

此外由聲子推遲格林函數還可以得到聲子局域態密度：

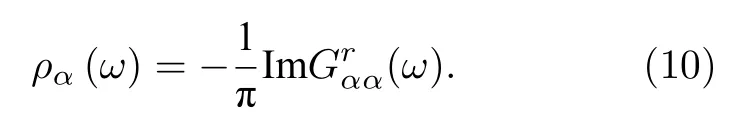
最后, 基于上述公式多晶石墨烯納米帶中的熱電品質因子ZT可以表示為

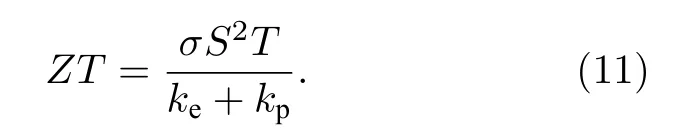
3 結果與討論

首先研究了晶界對石墨烯納米帶聲子輸運性質的影響.圖2(a)顯示了完美石墨烯納米帶和具有不同晶界數的石墨烯納米帶聲子熱導κph隨溫度的變化.需要指出的是, 圖2(a)中多晶石墨烯納米帶的熱導數據為統計平均后的結果.為了獲得該結果, 在計算中統計了至少20個不同的多晶石墨烯納米帶樣品.從圖2(a)可以明顯地觀察到, 多晶石墨烯納米帶的熱導遠遠低于完美石墨烯納米帶的值, 并且其還會隨著晶界數目的增加繼續降低.例如：在300 K時, 完美石墨烯的聲子熱導約為2.5 nW/K, 當系統中存在3個晶界時聲子熱導率僅為 0.26 nW/K, 而當晶界數目增加到 7 時, 聲子熱導率進一步下降至0.15 nW/K.為了理解這一現象, 計算了相應的聲子透射系數, 如圖2(b)所示.對于完美石墨烯納米帶, 可以發現聲子透射系數為量子化平臺狀, 并且其透射系數數值與聲子色散關系中的輸運通道相對應.而當系統引入晶界后, 輸運量子化平臺受到破壞, 聲子透射系數也急劇下降.這說明聲子在通過多晶石墨烯納米帶過程中受到了晶界強烈的散射.另外, 值得一提的是,在多晶石墨烯納米帶中, 低頻聲子盡管擁有較長的波長, 其仍然遭到了晶界的散射.為了更為直觀地展現出聲子在多晶石墨烯納米帶中的輸運行為,圖2(c)—(e)給出了3個典型頻率下的聲子局域態密度.可以看出, 這3個典型頻率的聲子均受到了極大的散射, 從而其主要局域在晶界附近沒有形成有效的輸運通道.也正是因為晶界的散射作用以及聲子輸運通道的破壞才導致了多晶石墨烯納米帶的熱導遠低于完美石墨烯納米帶的值.這些研究結果表明, 晶界散射行為對提高石墨烯納米帶的熱電性能將發揮積極作用.

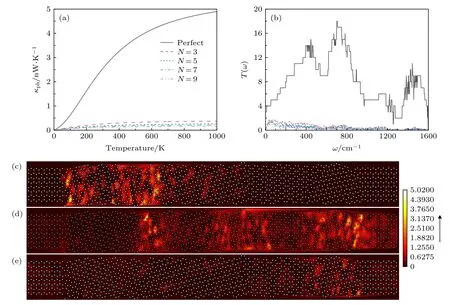
圖2 完美石墨烯納米帶和多晶石墨烯納米帶的 (a)聲子熱導和 (b)聲子透射系數 (其中 L = 196.48 ?, W = 17.04?);(c)(e)多晶石墨烯納米帶 (N = 5)在 3 個典型頻率下 (頻率分別是 160.68, 585.04, 951.72 Hz)的聲子局域態密度Fig.2.Comparison of (a) the phonon conductance, (b) the phonon transmission for perfect graphene nanoribbons and polycrystalline graphene nanoribbons (where L = 196.48 ?, W = 17.04 ?); (c)-(e) the local density of states in polycrystalline graphene (N = 5)at three typical frequency (160.68, 585.04 and 951.72 Hz).

圖3(a)給出了完美和多晶石墨烯納米帶的電子透射系數.采用的是鍵長依賴的緊束縛模型, 因此所獲得的電子透射系數要較先前基于最近鄰緊束縛模型所得到的結果更為優異和精確.與多晶石墨烯納米帶中的聲子情況類似, 晶界同樣會破壞電子的輸運通道并且對通過多晶結構的電子產生散射作用.因此, 從圖3(a)可以看到晶界破壞了完美石墨烯納米帶的電子輸運量子化平臺, 而且極大地降低了透射系數數值.隨著晶界數目的增加, 輸運通道進一步受到破壞, 散射作用也進一步增強, 因此多晶石墨烯納米帶的電子透射系數進一步下降.依據 (5)和(7)式, 可以發現電子電導和電子熱導均與電子透射系數直接關聯.因此, 如圖3(b)和圖3(c)所示, 電子電導和電子熱導同樣會隨著晶界的引入而急劇下降, 并隨著晶界數目的增加而進一步減弱.對于塞貝克系數而言, 其與電子透射系數的偏微分密切關聯.透射系數跳變越大, 塞貝克系數也會越大.從圖3(d)可以看到完美石墨烯納米帶的塞貝克系數峰位于—1.39, —0.62 和 0.59 eV附近.而對于多晶石墨烯納米帶, 晶界破壞了電子透射系數的量子化平臺, 產生了較多的峰谷結構.因此其塞貝克系數峰的分布更為廣泛, 并且其最大值也從完美石墨烯納米帶的0.066 mV/K提升至0.20 mV/K (N= 7).塞貝克系數的增強對于石墨烯熱電性能的提升發揮著積極的作用.同時分布更為廣泛的塞貝克系數峰也方便了實驗方面操作的實現.

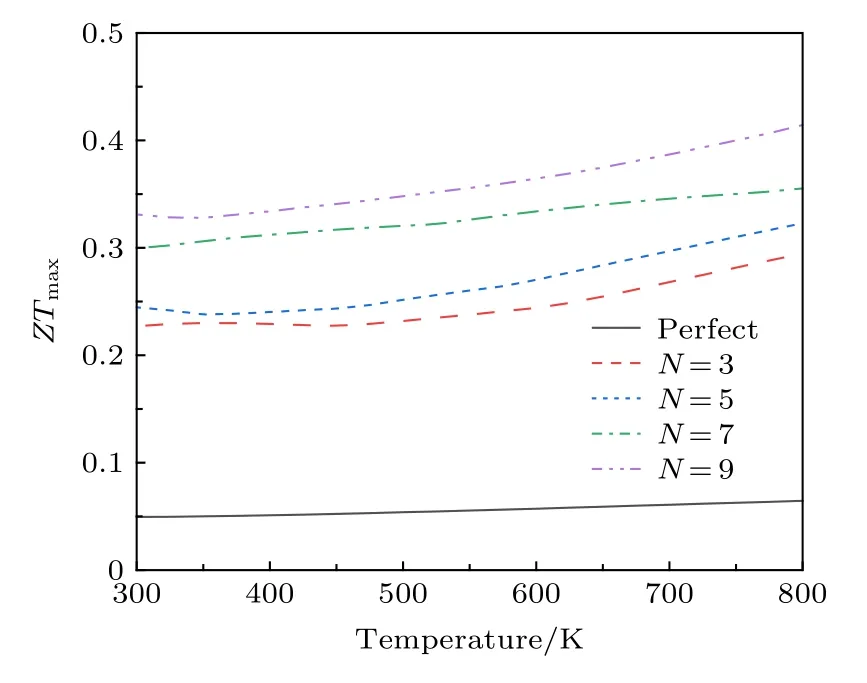
圖4 完美和多晶石墨烯納米帶的熱電品質因子隨溫度的變化Fig.4.Peak values of ZT as a function of temperature for perfect graphene nanoribbons and polycrystalline graphene nanoribbons.

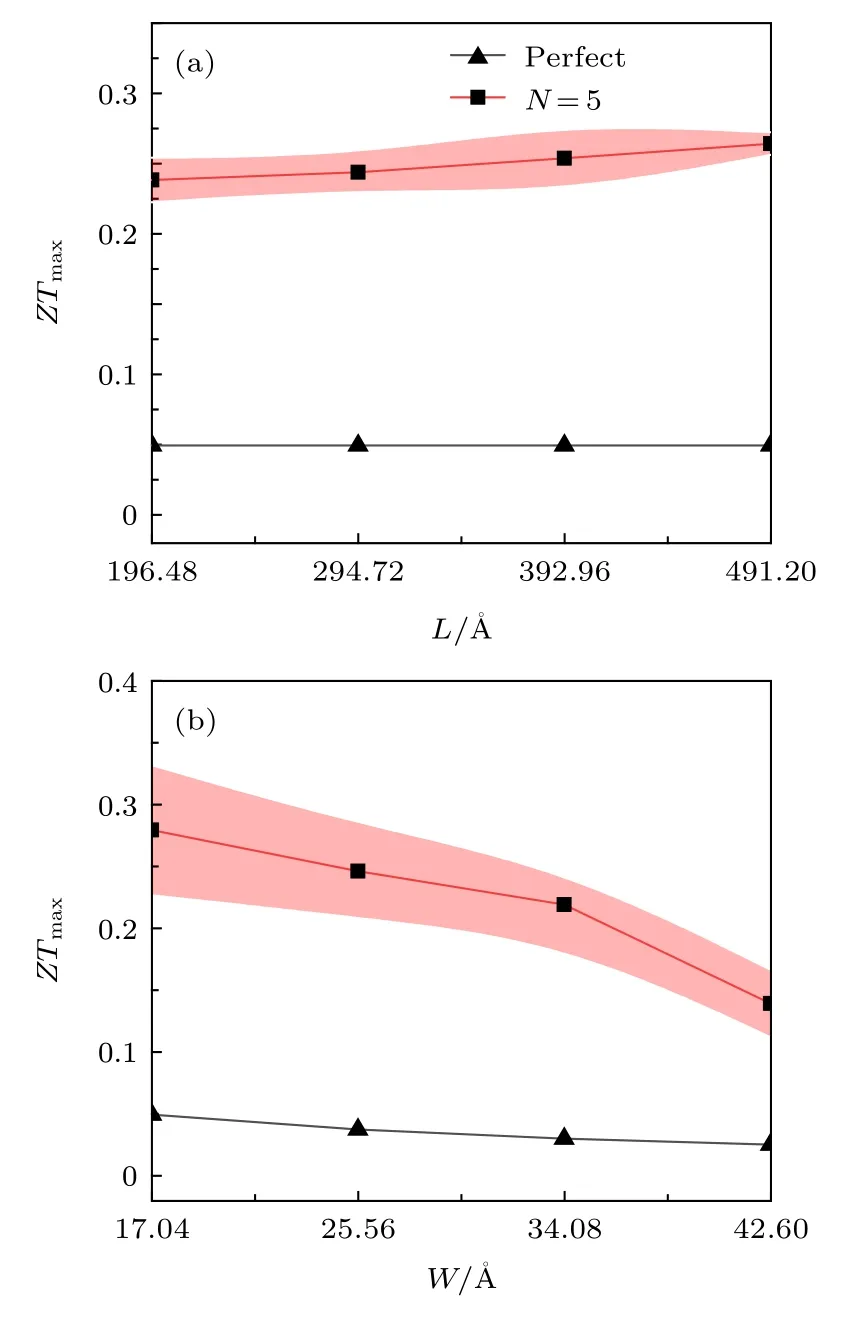
圖5 室溫下 (300 K), 完美與多晶石墨烯納米帶 (N = 5)熱電品質因子隨系統(a)長度L和(b)寬度W的變化(陰影部分為標準偏差)Fig.5.Peak values of ZT of perfect and polycrystalline graphene nanoribbons (N = 5) at room temperature as a function of (a) nanoribbon length or (b) nanoribbon width.The shading part corresponds to the standard deviation.

結合聲子和電子輸運性質的計算結果, 可以根據(11)式獲得多晶石墨烯納米帶的熱電品質因子,如圖4所示.在室溫下完美石墨烯納米帶的熱電品質因子約為0.049, 這與先前的理論計算預測基本一致.當結構中引入晶界后, 可以看到熱電品質因子得到了顯著的提升.在室溫下, 晶界的引入可將完美石墨烯納米帶的品質因子提高6倍左右(N= 7).然而, 從圖4 還可以發現溫度對于提升多晶石墨烯納米帶的熱電轉換效率并沒有明顯的積極作用, 這與先前對石墨炔熱電性質的研究略有不同[34].隨著晶界數目的增加, 多晶石墨烯納米帶熱電性能還能得到進一步的增強.該結果表明多晶化的確是提升石墨烯納米帶熱電性質的有效途徑.最后研究了系統的結構尺寸對于多晶石墨烯納米帶熱電性能的影響.如圖5(a)所示, 在固定晶界數目前提下, 增加石墨烯納米帶的長度會進一步提高石墨烯納米帶的熱電性能.這主要是由于單晶石墨烯晶粒長度的增加會使得低頻(長波長)聲子受到更多的散射.該行為將進一步削弱多晶石墨烯納米帶的熱導, 進而增強其熱電轉換效率.對于寬度效應,從圖5(b)中可以發現多晶石墨烯納米帶的熱電品質因子會隨著寬度的增加而逐漸下降.這主要歸因于較寬的完美石墨烯納米帶本征熱電性能低下所引起的.但是值得一提的是, 多晶石墨烯熱電性能提升的倍率并未隨著寬度的增加而顯著下降.綜上所述, 為了獲得更為優異的熱電性能, 應該選取較長的且寬度適中的多晶石墨烯納米帶.

4 結 論

本文采用非平衡格林函數方法系統地研究了晶界對石墨烯納米帶熱電性能的調控作用.研究結果表明：晶界能有效地提高石墨烯納米帶的塞貝克系數, 同時可以極大地抑制其電子和聲子熱導.基于這兩個積極的效應, 多晶石墨烯納米帶的熱電轉換性能得到了明顯的增強.在室溫下, 多晶石墨烯納米帶的熱電品質因子約為0.3, 比完美石墨烯納米帶(約為0.05)提升了6倍左右.此外, 還發現晶界的數量以及系統的長度能進一步提升多晶石墨烯納米帶的熱電性質, 而系統的寬度對其影響有限.這些研究結果表明多晶結構能夠有效提升石墨烯納米帶的熱電轉換效率, 并為設計和制備基于石墨烯納米帶的熱電器件提供了新的途徑.