數字信號處理中信噪比影響因素分析

孫書良，解 劍，羅顯志，劉 亮

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081；2.衛星導航系統與裝備技術國家重點實驗室，河北 石家莊 050081)

0 引言

數字信號處理在信號表達形式上可分為2個階段：模擬信號數字化階段和數字信號處理階段。模擬信號數字化需要采用模數轉換器(Analog Digital Converter，ADC)實現，而數字信號處理主要基于數字信號處理芯片實現。

模擬信號在經過ADC數字化后，其信噪比會發生變化，這主要是因為AD器件本身存在量化誤差等問題，導致ADC性能不夠理想。當前形勢下，數字信號處理向高精度、高性能方向發展，對影響信號性能的因素需要進行深入研究。文獻[1-2]對模擬信號數字化過程中的量化誤差和有限字長效應等因素進行了分析，隨著ADC位數的增加，ADC引入的誤差逐漸減小，但是對ADC的有效位數對信噪比的影響沒有進行分析。文獻[3]對信號處理中各處理環節噪聲系數對系統總體噪聲系數的影響和其在系統所處的位置有關，越靠近前級對系統的噪聲系數影響越大，但是對于數字信號處理階段內部影響信號的信噪比、信噪諧波比等因素未進行詳細分析。

試驗過程中發現，數字信號處理階段也會對數字化之后的信號產生影響。數字信號處理涉及到大量的乘加、濾波等運算，考慮到硬件邏輯資源的開銷、功耗等問題，數字信號處理階段不可避免需要用到數據截位等操作；在變頻、解擴等信號處理過程中，需要產生相應的本地信號，本地信號的信噪比也會對變頻、解擴后的信號的信噪比產生影響。

本文詳細分析了模擬信號數字化和數字信號處理2個階段中信號的信噪比和有效位數的變化，并重點仿真了數字信號處理階段信號的信噪比和有效位數，提出了在數字信號處理過程中保持較高信噪比的方法，對于設計高性能的信號處理平臺具有很好的借鑒意義。

1 AD器件信噪比和有效位數

1.1 AD器件信噪比和量化位數

AD器件完成將模擬信號到數字信號的轉化，是數字信號處理系統中必不可少的部分[1]。而且由于AD器件位于整個系統的前級位置，根據信號處理的級聯系統原理，設備在系統中的位置越靠前，其性能對系統的信噪比影響越大[2]。因此，AD器件的性能對數字信號處理系統的性能具有很大影響。

衡量AD器件的主要性能有采樣率、量化位數、信噪比、線性度、有效位數和交調等參數，其中有效位數和信噪比是對AD器件性能影響較大的指標[3-4]。

理想N位量化的AD器件的信噪比主要由量化噪聲導致[5]，量化噪聲是一個服從[-Δ/2，Δ/2]均勻分布的隨機變量，其中Δ為量化電平，在輸入信號達到AD器件滿量程的情況下，信噪比和量化位數具有如下數值關系[6]：

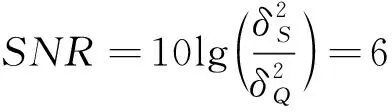
(1)

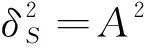
1.2 AD器件有效位數

有效位數也是AD器件的重要參數。量化位數為N的AD器件，其有效位數要小于N。有效位數的計算，不僅考慮AD器件的信噪比，還將AD器件的諧波也考慮在內，能夠更好地表征AD器件采集信號的性能。AD器件的有效位數計算主要有FFT法和正弦擬合法等方法[7-8]。

基于FFT法的計算原理主要是在保證AD器件滿量程情況下對信號進行采集，對采集的時域數據進行FFT運算，得到采樣信號的傅里葉頻譜。然后從頻譜中計算信號、噪聲和諧波分量的功率，進而求出信噪諧波比(SINAD)，并計算出有效位數：

(2)

正弦擬合法將采樣后的信號X(nTs)以正弦函數為回歸模型用最小二乘法對采樣序列進行擬合，得到擬合后的函數XF(t)，并對擬合后的函數進行N位無量化誤差的理想采樣XFD(nTs)，計算原始采樣序列X(nTs)，和擬合后采樣序列XFD(nTs)的之間的均方根誤差e，計算得到ADC采樣信號的有效位數：

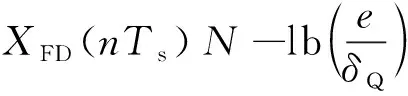
(3)

通過以上分析可以看出，AD器件的信噪比和量化位數具有線性關系，隨著量化位數的增加，信噪比也增加，反之亦然。AD器件的有效位數，不能等同于量化位數，通常要小于量化位數，量化位數的增加，有效位數也隨之增加。因此，在對信噪比要求較高的系統中，要盡量選擇量化位數高的AD器件，同時要選擇合適的輸入信號幅度，盡量接近AD器件的滿量程，才能保證較高的有效位數。

2 數字信號處理階段信噪比和有效位數

2.1 簡單的信號處理模型

通過上面的分析可以看出，AD器件作為數字信號處理的第一個環節，AD器件性能會對數字化信號的信噪比產生較大影響。數字化的信號，將被送入數字信號處理程序處理。數字信號處理階段作為信號處理的第二個階段，處理方法的性能好壞，對信號處理結果同樣具有較大影響。

簡單來說，數字信號處理過程中主要涉及的運算可以歸納為乘加、濾波和FFT變換等運算，對數據信號質量會產生影響[9]。運算的過程也是一個信號位寬擴展的過程，其中，乘法對于信號位寬的擴展尤為明顯。比如，2個8位數字信號相加，需要9位信號才能對結果進行無差錯的表示；2個8位數字信號相乘，需要16位信號才能對結果實現無差錯的表示。數字信號通常會包含多次的乘加運算，隨著乘加操作的增多，信號的位寬會迅速增加，需要耗費的邏輯資源變得愈發龐大。考慮到硬件邏輯資源的開銷、功耗等問題，需要對數據進行截位操作，截位使數據位寬變小，也會對信號產生影響。不得當的截位方式會導致直流偏置，影響后續的信號處理操作。

在導航、通信等信號處理系統中，變頻、濾波和解擴等處理手段必不可少[10-11]。在變頻處理中，需要產生本地載波信號，用來對輸入信號進行混頻，對信號變換到基帶進行處理。本地載波信號的信噪比也會對變頻、解擴后的信號的信噪比產生影響。混頻后信號需要進入濾波器進行濾波，濾除高頻分量，最終得到基帶信號。在濾波器設計環節得到的濾波器系數一般都會包含小數部分。在硬件平臺中實現相應的濾波器，需要對濾波器的系數進行近似，這也會降低濾波器的精度，進而影響信號處理結果的信號性能[12]。

考慮到變頻、濾波等處理中最主要的運算就是乘法，針對信號處理過程中的處理方法進行分析，仿真了在輸入信號采用16 bit量化，本地載波采用不同量化位數的情況下，本地信號以及相乘結果截位前后的信號的信噪比和有效位數。其中，相乘處理的框圖如圖1所示。

圖1 變頻處理框圖

仿真工具采用Matlab軟件。在Matlab中，數據使用double類型表示，可以對浮點數進行高精度的表示[13]。本文分別仿真了AD器件對模擬信號進行采樣和量化時，不同量化位數對本地載波信號質量的影響；在數字信號處理過程中，本地載波信號不同量化位數情況下，信號處理結果的信號質量；以及數據截位操作對處理結果信號質量的影響。并對SNR，SINAD，ENOB三者之間的關系進行了討論。

具體仿真步驟如下：

① 按照50 MHz采樣率，產生頻率為3.3 MHz輸入信號，并對輸入信號按照16 bit進行量化，模擬AD器件對信號的處理過程；

② 按照50 MHz采樣率，產生頻率為8.6 MHz的本地載波信號，并按照2，4，6，8，10，12 bit分別對本地信號進行量化，分析不同量化位數對信號質量的影響；

③ 將量化后的輸入信號和本地信號相乘，得到變頻后的信號，分析不同量化位數對信號處理結果的影響；

④ 按照輸入信號的量化位數，即16 bit對輸入信號進行截位，分析數據截位對信號質量的影響；

⑤ 分別測試輸入信號、本地信號和未截位的變頻信號，截位后的變頻信號信噪比、信噪諧波比和有效位數等參數。

2.2 測試結果與分析

為了更全面地對信號的信噪比、信噪諧波比和有效位數等參數進行測試，采用FFT方法對信號進行測試。得到輸入信號的信噪比為46.98 dB，信噪諧波比為46.98 dB，輸入信號有效位數為13.5 bit，不同的本地信號量化位數時，本地信號、未截位的變頻信號和截位后的變頻信號的各項分析結果如表1所示。

表 1 不同量化位數測試結果

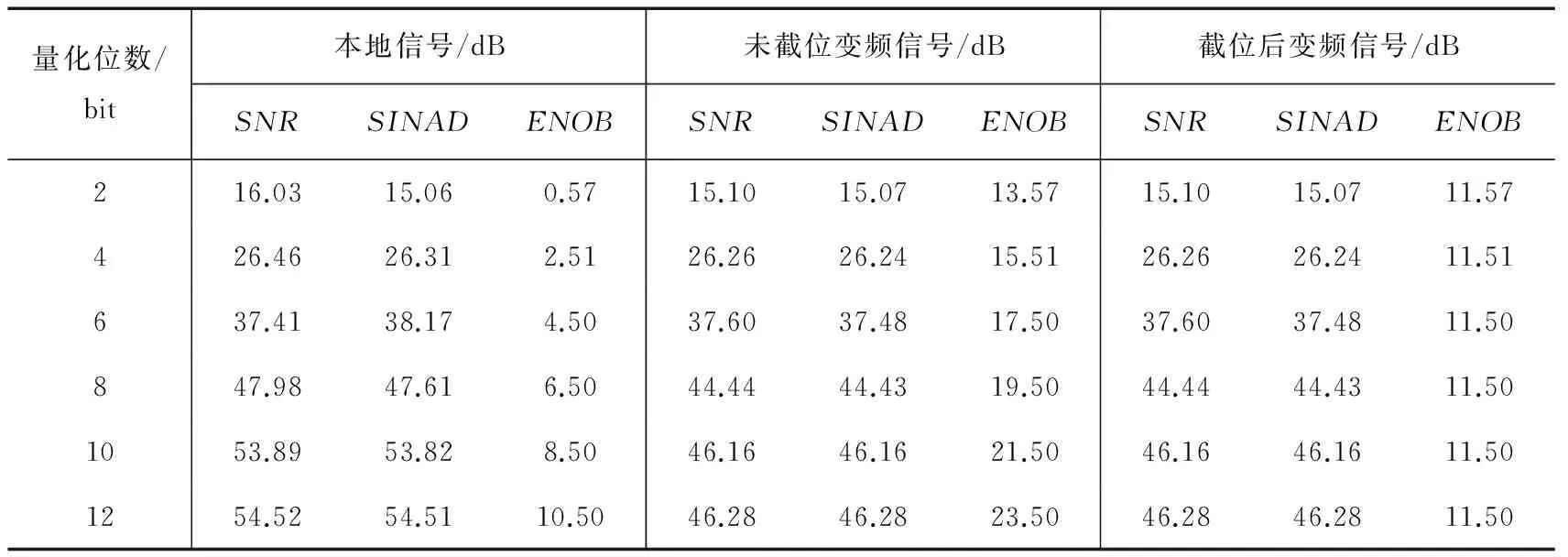
量化位數/bit本地信號/dB未截位變頻信號/dB截位后變頻信號/dBSNRSINADENOBSNRSINADENOBSNRSINADENOB216.0315.060.5715.1015.0713.5715.1015.0711.57426.4626.312.5126.2626.2415.5126.2626.2411.51637.4138.174.5037.6037.4817.5037.6037.4811.50847.9847.616.5044.4444.4319.5044.4444.4311.501053.8953.828.5046.1646.1621.5046.1646.1611.501254.5254.5110.5046.2846.2823.5046.2846.2811.50

通過對比不同量化位數，信號處理截位前后的信號指標測試結果，可以得出如下結論：

① 隨著量化位數的增加，本地信號SNR，SINAD，ENOB逐漸提升；

② 隨著量化位數的增加，未截位變頻信號的SNR，SINAD，ENOB逐漸提升；

③ 隨著量化位數的增加，截位后變頻信號的SNR，SINAD逐漸提升，但ENOB基本維持不變，甚至略有下降；

④ 當量化位數達到10 bit以上時，量化位數增加帶來的SNR，SINAD，ENOB改善程度變小；

⑤ 相比于截位前，截位后的變頻信號ENOB有所下降，而SNR，SINAD沒有變差。

由此，為了保證變頻后信號的信噪比和有效位數，可以對本地信號的量化位數盡量大，考慮到資源的消耗和信噪比的折中，不需要過于追求增加本地信號量化位數，在量化位數8，10 bit左右即可達到較高的信噪比。

同時，還注意到，信號處理過程中測試結果中的量化位數，SNR，SINAD，ENOB四者的關系不滿足1.1節和1.2節中AD器件四者之間關系的公式，這主要是因為：

① 數字信號處理過程與AD器件的模數轉換過程具有不同的特性；

② 得到這些公式的前提是保證AD器件采集信號時，信號幅度剛好能達到AD器件的滿量程，而在信號處理過程中，信號并不是滿量程的。

3 結束語

詳細分析了模擬信號數字化和數字信號處理2個階段中影響信號處理結果信噪比和有效位數的幾個因素，并基于簡單的信號變頻模型，仿真了數字信號處理系統中產生的本地信號對處理結果的信噪比、信噪諧波比和有效位數等性能的影響。通過仿真發現，本地信號的量化位數對信號處理結果的信噪比和信噪諧波比有較大影響，對信號處理結果的有效位數沒有明顯影響。建議在數字信號處理過程中，選取足夠的量化位數，來保證數字信號處理結果具有較高的信號比和信噪諧波比，對數字信號處理系統的設計具有很好的借鑒意義。