一種基于雙樹復小波變換的圖像去噪算法

畢思文，陳 浩，帥 通，李 娜

(1.中國電子科技集團公司航天信息應用技術重點實驗室，河北 石家莊 050081；2.中國科學院遙感與數字地球研究所，北京100101)

0 引言

數字圖像在成像和傳輸過程中，經常會受到各種各樣的噪聲干擾[1]。為了使后期的圖像理解和圖像分割等操作更加有效，需要對受到噪聲干擾的圖像進行處理。

在圖像去噪方面，人們提出了許多圖像去噪算法，文獻[2] 提出基于Cycle Spinning的圖像自適應閾值去噪方法，該方法提高了去噪圖像峰值信噪比(PSNR)，降低了均方誤差(MSE)，去噪圖像清晰，獲得較好的視覺效果。 文獻[3]通過平穩小波變換對圖像進行小波分解，對于子圖像的高頻區域進行閾值分割和雙邊濾波，利用平穩小波更好的冗余性和平穩不變性，更好地去除了SAR圖像的相干斑噪聲，實驗表明這種改進的去噪方法對SAR圖像的相干斑噪聲有很好的抑制效果。文獻[4]提出了一種新方法來濾除圖像中的云霧，結果表明，該算法優于傳統濾波方法，且對于薄云圖像效果更佳。 文獻[5]在經典小波閾值去噪算法的基礎上改進了閾值函數，提出了一種新的小波閾值去噪算法，實驗結果表明該算法提高了信號特征的可分離性，具有較高的實用價值。

小波分析是為了彌補短時傅里葉變換的不足而發展起來的一門應用數學學科[6]。基于小波分析的去噪方法最早由Mallat提出，他在1992年建立了小波變換快速算法，并將其運用在信號和圖像的分解和重構中[7]。1999年，Kingsbury提出了雙樹復小波變換(Dual Tree Complex Wavelet Transform，DTCWT)，具有平移不變性，提供了6個方向的信息，因而具有較好的方向性和精確的相空間信息[8]。在DTCWT提出以后，有很多學者在基于雙樹復小波的去噪方法方面做了大量研究。文獻[9]提出了一種基于雙樹復小波變換和形態濾波的去噪算法。文獻[10]提出了一種基于非下采樣雙樹復小波域的圖像去噪算法，實驗表明該算法比經典算法提高了一定的峰值信噪比，且有良好的視覺效果，較好地保持了圖像中的紋理特征。文獻[11]綜合考慮空域濾波和變換域濾波的優點，提出了一種基于DTCWT和自適應窗的圖像去噪算法，將雙樹復小波變化和自適應橢圓窗口濾波相結合，考慮了小波分解的不同子帶具有不同的能量方向，以橢圓方向窗作為領域，獲得了比較好的去噪效果。但文獻[11]中使用的橢圓窗作為鄰域，系數估計時均需要采用橢圓模板進行匹配，所以算法運行時間較長、復雜度略高。

本文借鑒多量子位量子疊加態的測量坍縮原理，根據雙樹復小波較好的方向特性，以坍縮后的狀態作為鄰域計算小波系數方差，利用雙樹復小波提供的方向信息和量子疊加態的測量坍縮原理運用到圖像去噪中進一步去噪。實驗結果表明，本文提出的圖像去噪算法與文獻[11]的圖像去噪方法相比，去噪性能得到改善，運行時間明顯提升。

1 雙樹復小波變換

DTCWT變換可以通過兩對濾波器組同時作用在輸入數據上來實現。復小波可以表示為：

ψ(t)=ψr(t)+jψi(t)，

(1)

式中，Ψr(t)表示復小波的實部；Ψi(t)表示復小波的虛部。Ψr(t)，Ψi(t)都是實函數，因此，DTCWT可以表示為2個獨立的實小波變換，包含了2個平行的小波樹：樹a和樹b。DTCWT分解示意圖如圖1所示，樹a和樹b的疊加濾波器組分別表示復數小波變換的實部和虛部，↓2表示隔點采樣[12]。為了保證濾波器的沖擊響應對應于復小波變換系數的實部和虛部，采用2棵樹的濾波器長度分別為奇數和偶數且是線性相位。基本原理就是利用一對實濾波樹，同時對輸入信號進行分解，產生小波系數的實部和虛部。

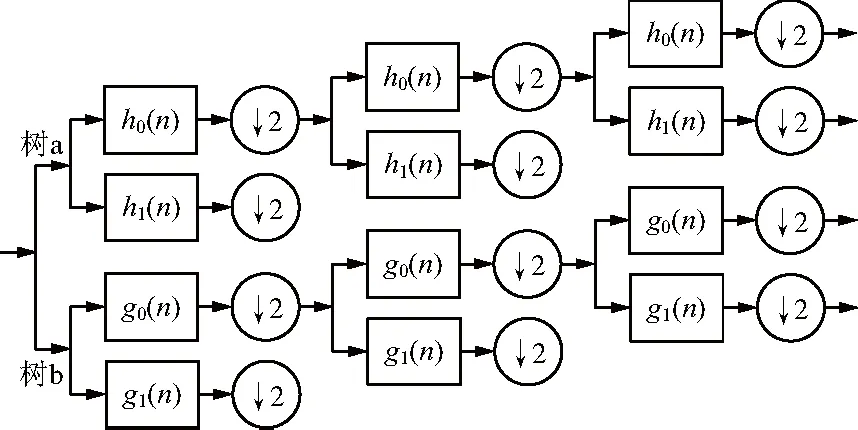
圖1 DT-CWT分解示意

二維的雙樹復小波實部與虛部小波系數能提取±15°，±45°，±75°六個方向的高頻信息，相對離散小波變換(Discrete Wavelet Transform，DWT)具有近似平移不變性、多方向選擇性、更高定位精度和計算效率等優點[13]。相比之下，DWT在每個尺度上有3個小波子帶，只能反映出水平數豎直和對角方向。二維DT-CWT在空間域和在2-D平面內(理想化的)表示出具有6個不同的角度DT-CWT小波如圖2所示。

圖2 DT-CWT的脈沖響應及在二維平面等效

2 量子疊加態的測量坍縮原理

2.1 態疊加原理

若|Ψ1〉是Hilbert空間中的一個矢量，|Ψ2〉是另外一個矢量，由態疊加原理可知：

|Ψ〉=c1|Ψ1〉+c2|Ψ2〉，

(2)

也是Hilbert空間中的一個矢量。其中c1，c2分別是狀態|Ψ1〉|Ψ2〉的概率幅。且滿足歸一化條件：

c12+c22=1。

(3)

所以若量子系統處在|Ψ1〉和|Ψ2〉描述態中，則式(2)的線性疊加態|Ψ〉也是該系統的一個可能態，這就是量子力學的態疊加原理[14]。量子比特[15](qubit)是量子信息理論中的一個重要概念，對一個具有2個基態的雙態量子系統[16]。若將2個基態分別記為|0〉和|1〉，記量子比特為：

|Ψq〉=a|0〉+b|1〉。

(4)

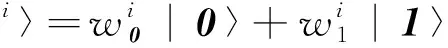
|Ψ〉= |Ψ(1)〉 |Ψ(2)〉…|Ψ(n)〉=

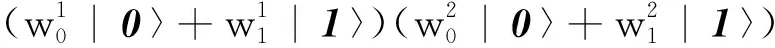
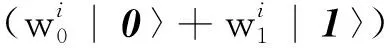
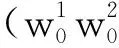
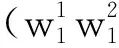
(5)

式中，|i〉表示第i個基態；ωi為基態|i〉的概率幅，滿足歸一化條件：

(6)

2.2 量子疊加態的測量坍縮

由量子力學第三假設可知，設測量算子由{Mm}描述，測量前量子系統的最新狀態是|Ψ〉，則測量后系統的狀態為[17]：

(7)

為了更好地理解量子測量坍縮原理，舉例如下：對于一個4×4的疊加態結構元素(歸一化以后)，若另取一個4×4的陣列，將陣列中邊緣的最大的2個灰度值取為1，其余取值為0，則得到{Mm}，對應|iM〉=|0001000000001000〉，若用此測量算子Mm=|0001000000001000〉〈00010000000010000|對鄰域圖像進行測量，則鄰域圖像將坍縮到基態|iM〉，如圖3所示。

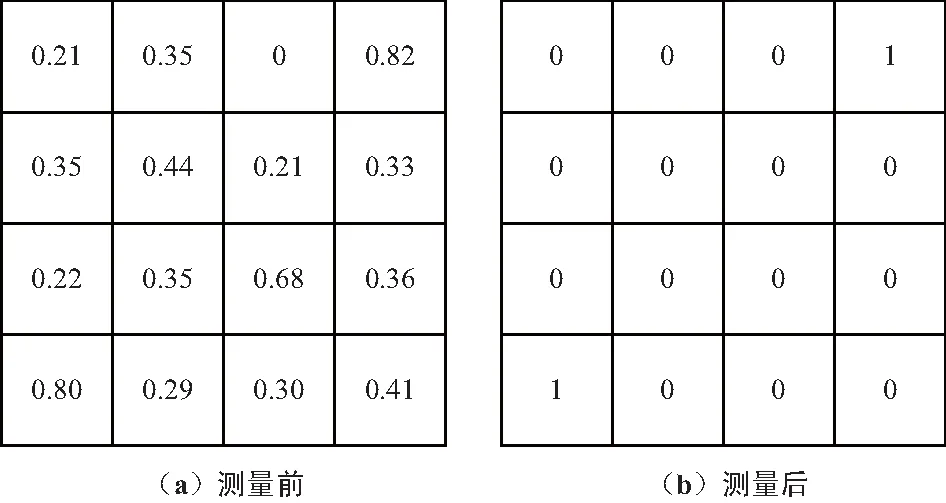
圖3 測量前和測量坍縮以后

由于圖像中不同點之間領域的特征不一樣，所以在不同移動點所得到的測量算子和測量后的坍縮態也不同[18]。以上就是雙樹復小波變換以后，計算+45°方向鄰域，其他方向類似。

3 本文提出的改進算法

3.1 算法模型

假設原始圖像被均值為0，方差為σ2的高斯白噪聲污染，當在小波域通過小波變換系數進行去噪后采用以下模型：

Y(i，j)=X(i，j)+N(i，j)，

(8)

式中，Y(i，j)為含噪小波系數；X(i，j)為待估計的干凈小波系數；N(i，j)為噪聲小波系數。采用MAP預估器可表示為：

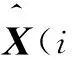
(9)

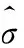
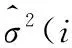
(10)

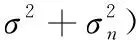
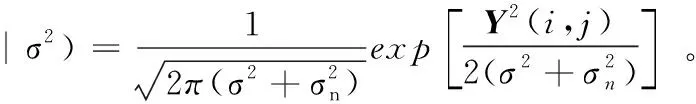
(11)

將式(10)帶入式(9)，并對其進行求導，令其導數為零可得：

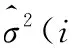
(12)

式中，M為鄰域N中系數的個數。若已知圖像信號的方差分布，那么由最大后驗概率估計(Maximum A Posterior，MAP)可得：

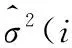
(13)

式中，fσ(σ2)為圖像信號的方差分布。由式(13)推導可得：

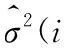
(14)

3.2 算法流程

根據以上算法模型，本文去噪算法步驟如下：

① 對圖像進行雙樹復小波變換；

② 利用量子態疊加的測量坍縮原理，以4×4的陣列測量分解層；

③ 以坍縮后的鄰域用式(8)和式(11)計算λ；

④ 重復步驟②，然后利用式(13)估計雙樹復小波系數的方差；

⑤ 利用式(8)得到去噪以后的系數；

⑥ 雙樹復小波反變換，得到去噪后的圖像。

4 實驗驗證與分析

為了驗證本文所提算法的有效性，實驗中選用標準的512×512大小的8位灰度圖像作為實驗對象。實驗中，假定用均值為0、標準差分別為10，15，20高斯白噪聲污染，對測試圖像進行4層的下采樣雙樹復小波分解。在文獻[19]中指出，對包含了高斯噪聲的圖像進行3級小波分析，并對高斯噪聲小波系數的分布情況進行了統計分析，發現大約有96%的噪聲系數分布在最外2層的細尺度子帶中[20]。因此，對第二、第三和第四分解層，采用利用量子態疊加測量坍縮原理，選取4×4的陣列中四周最大的2個值取值為1，其他的取為0，以此作為雙樹復小波分解以后的主方向，并且在此方向上作為系數估計的鄰域。將本文所提算法和文獻[11]做比較(PSNR 和運行時間)。

實驗效果圖和文獻[11]的數據對比結果如圖4和圖5所示。

圖4 2種去噪算法結果比較(Lena)

圖5 2種算法去噪結果比較(Barbara)

表 1 2種不同去噪方法得到的PSNR值比較

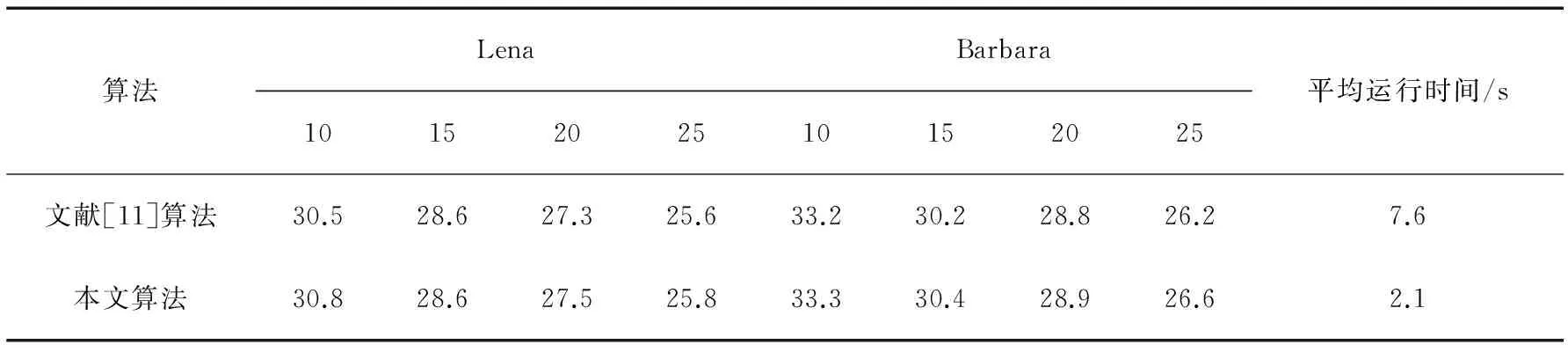
算法LenaBarbara1015202510152025平均運行時間/s文獻[11]算法30.528.627.325.633.230.228.826.27.6本文算法30.828.627.525.833.330.428.926.62.1

通過表1可以看出，利用本文所提算法得到的PSNR值比文獻[11]要略高，從處理以后的效果圖來看，本文所提算法有相同的抑制噪聲的能力，但由于本文所提算法將量子態疊加的測量坍縮原理與雙樹復小波變換相結合，將坍縮狀態作為計算子帶的方向窗，既利用了雙樹復小波變換的方向特性，同時避免了文獻[11]中每次系數估計時都要進行模板匹配的操作，因此，在運行時間上比文獻[11]有很大的提高。

5 結束語

本文將雙樹復小波變換和量子態疊加的測量坍縮原理相結合，利用雙樹復小波變換較好的方向特性和疊加態結構元素在不同位置坍縮為不同大小和形狀的屬性，避免了方形結構元素所不具備的方向性特性和橢圓結構元素帶來的復雜性。通過實驗發現，將量子力學中的理論運用到圖像去噪中，大大提升了運行速度并驗證了本文算法的有效性。該算法雖然在運行時間上相對于其他方法有較高提升，但是在評價指標PSNR數據上的提高并不明顯，需要對算法進行優化改進，仍有較大的提升空間。