湍流度對斜拉索雷諾數效應影響的試驗研究

劉慶寬，趙桂辰，安 苗，賈婭婭，馬文勇，劉小兵

(1.石家莊鐵道大學 大型結構健康診斷與控制研究所，石家莊 050043； 2.河北省大型結構健康診斷與控制重點實驗室，石家莊 050043； 3.石家莊鐵道大學 土木工程學院，石家莊 050043)

大跨徑斜拉橋斜拉索由于自身的結構特點使得風荷載及其響應問題變得尤為重要和突出。影響斜拉索氣動性能的主要因素有雷諾數、表面粗糙度、來流湍流度等，這些影響因素之間互相關聯、互相制約。

其中，斜拉索的雷諾數效應一直是被關注的重要基礎問題，國內外學者對斜拉索的雷諾數效應研究較多，詳細的研究了斜拉索氣動力隨雷諾數的變化規律[1-6]。然而實際工程中斜拉索處于復雜的湍流環境中，風洞試驗研究斜拉索氣動參數的雷諾數效應問題一般都在來流湍流度強度很低的風洞中進行。因此在研究斜拉索氣動參數的雷諾數效應問題中考慮湍流強度的影響十分有必要。Surry等[7-9]研究了湍流度對斜拉索模型表面壓力系數的影響，發現湍流度對斜拉索表面的平均壓力系數及脈動壓力系數均有影響。在研究中得出Re越小，不同湍流度的壓力系數值相差越大，而在大Re下，其值越接近。Batham等[10-12]研究了不同湍流度下的氣動力系數，得知湍流度對氣動力系數影響很大。目前，關于來流湍流度對斜拉索氣動性能影響的研究仍很缺乏，相關試驗研究有待補充。

本文考慮實際大跨度斜拉橋的斜拉索所處風場中的湍流度，分別在均勻來流和2.4%、4.5%、5.6%、8.0%及11.0%的湍流度下對斜拉索模型進行了測壓試驗，對比分析了同一湍流度下斜拉索氣動力系數隨雷諾數的變化規律，以及不同雷諾數及同一雷諾數不同湍流度下的斜拉索氣動力系數隨湍流度的變化規律，為今后的斜拉橋結構設計和相關試驗研究提供參考。

1 風洞試驗

1.1 試驗條件

風洞試驗在石家莊鐵道大學風工程研究中心STU-1風洞的低速試驗段內進行，試驗段寬4.38 m，高3.0 m，長24.0 m，最大風速30.0 m/s，背景湍流度小于等于0.2%，風洞的平面結構如圖1所示。

圖1 風洞結構平面圖

1.2 試驗模型與試驗工況

斜拉索模型采用圓形斷面[13-14]，由有機玻璃圓管制成，表面光滑，直徑D=450 mm，長度L=2 500 mm，豎直放置在風洞的轉盤中心處，通過連接件與風洞頂部固定。使用微型壓力掃描閥測量斜拉索表面壓力，采樣時間為30 s，頻率為330 Hz。通過眼鏡蛇三維脈動風速測量儀(Cobra Probe)測得的模型上游與格柵之間來流的風速，同時測量洞體內溫度、相對濕度和大氣壓，以計算試驗的雷諾數。本試驗的雷諾數范圍為8×104到4.2×105之間，通過調節風速得到不同的試驗雷諾數，采用格柵、尖劈、粗糙元等實現不同的來流湍流度。

試驗的湍流度以蘇通長江公路大橋的斜拉索為參考確定。該橋斜拉索共有8種規格，其中A1索索塔上部錨固端高出常水位226 m，錨固的梁面高出常水位74 m[15-18]，按照規范湍流度沿高度的分布根據下式計算：

(1)

(2)

由公式計算出74 m高度處在A類地貌下湍流度為9.4%，B類地貌下的湍流度為10.4%，湍流度隨高度的增加而減小。具此，本試驗采用的最大湍流度定為11.0%，其它湍流度工況分別為8.0%、5.6%、4.5%、2.4%及均勻流，能夠覆蓋A類地貌及B類地貌下斜拉索整個高度范圍內的湍流度。

2 氣動力系數試驗結果分析

將試驗測得的風壓系數通過公式(3)～(6)計算得到不同湍流度下斜拉索模型的平均氣動力系數和脈動力系數隨雷諾數的變化規律。

(3)

(4)

(5)

(6)

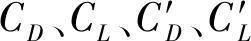
不同湍流度下斜拉索模型的平均阻力系數和脈動阻力系數隨雷諾數的變化如圖2和圖3所示。由圖2可見當來流為均勻流的時候，在亞臨界狀態，平均阻力系數基本保持在1.0左右；隨著雷諾數的增加，大概在3.5×105左右進入臨界狀態時，平均阻力系數開始大幅度下降，下降到最低點之后保持平穩。而當來流湍流度為2.4%時，平均阻力系數在雷諾數大約為1.1×105時就開始大幅度下降了，并且在雷諾數約為2.4×105時平均阻力系數就已經下降到最低點并保持穩定。當湍流度增加到4.5%時，在試驗測得的最小雷諾數約為8.0×104時平均阻力系數就已經處于迅速下降的階段了，而在雷諾數約為1.8×105時下降到最低點。當湍流度繼續增加到11.0%時，在雷諾數約為1.0×105時平均阻力系數就已經下降到最低點進入超臨界狀態。由此可見，湍流度的存在使得斜拉索的雷諾數效應提前，并且湍流度越大氣動參數的雷諾數效應提前的越明顯。

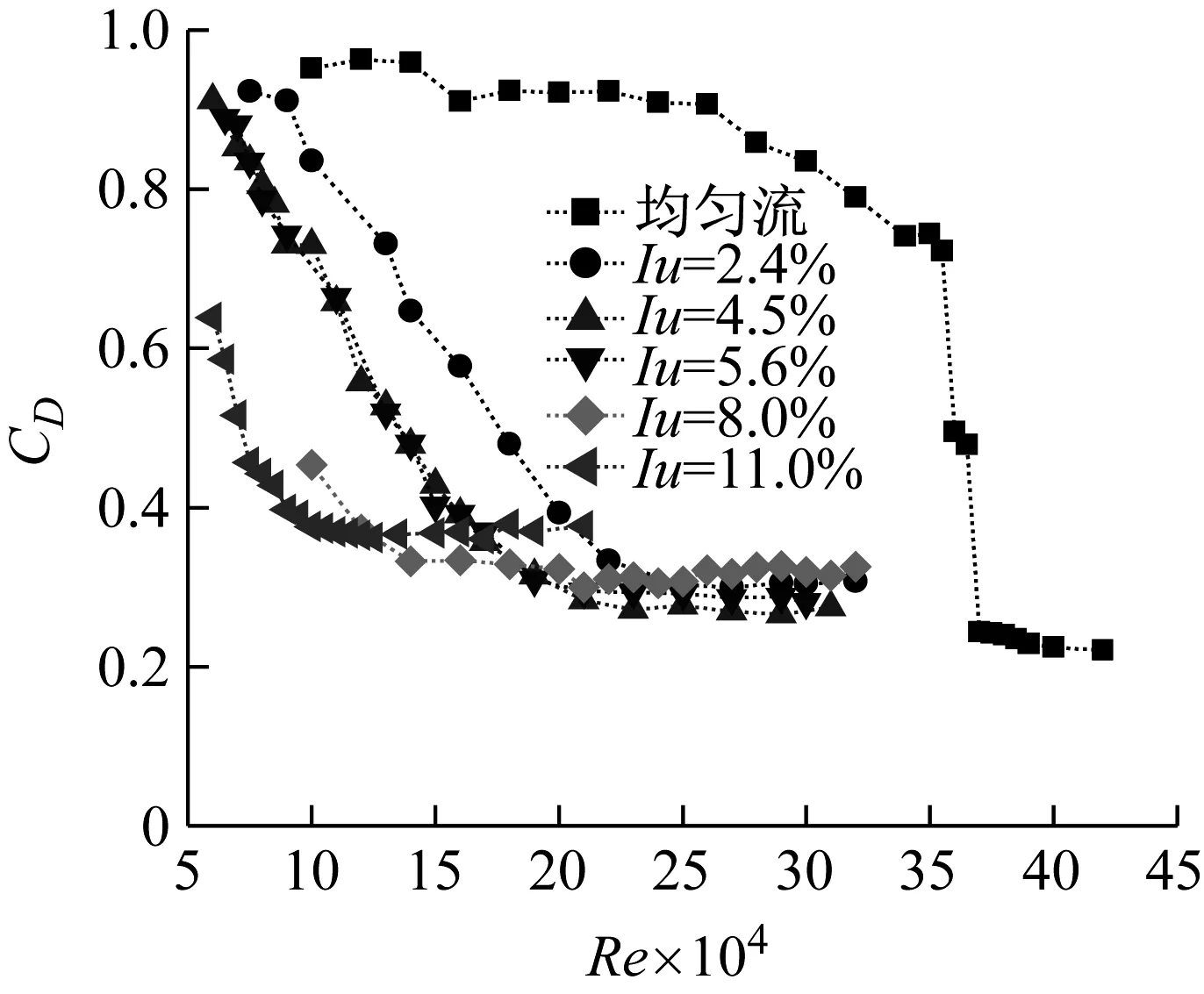
圖2 平均阻力系數曲線

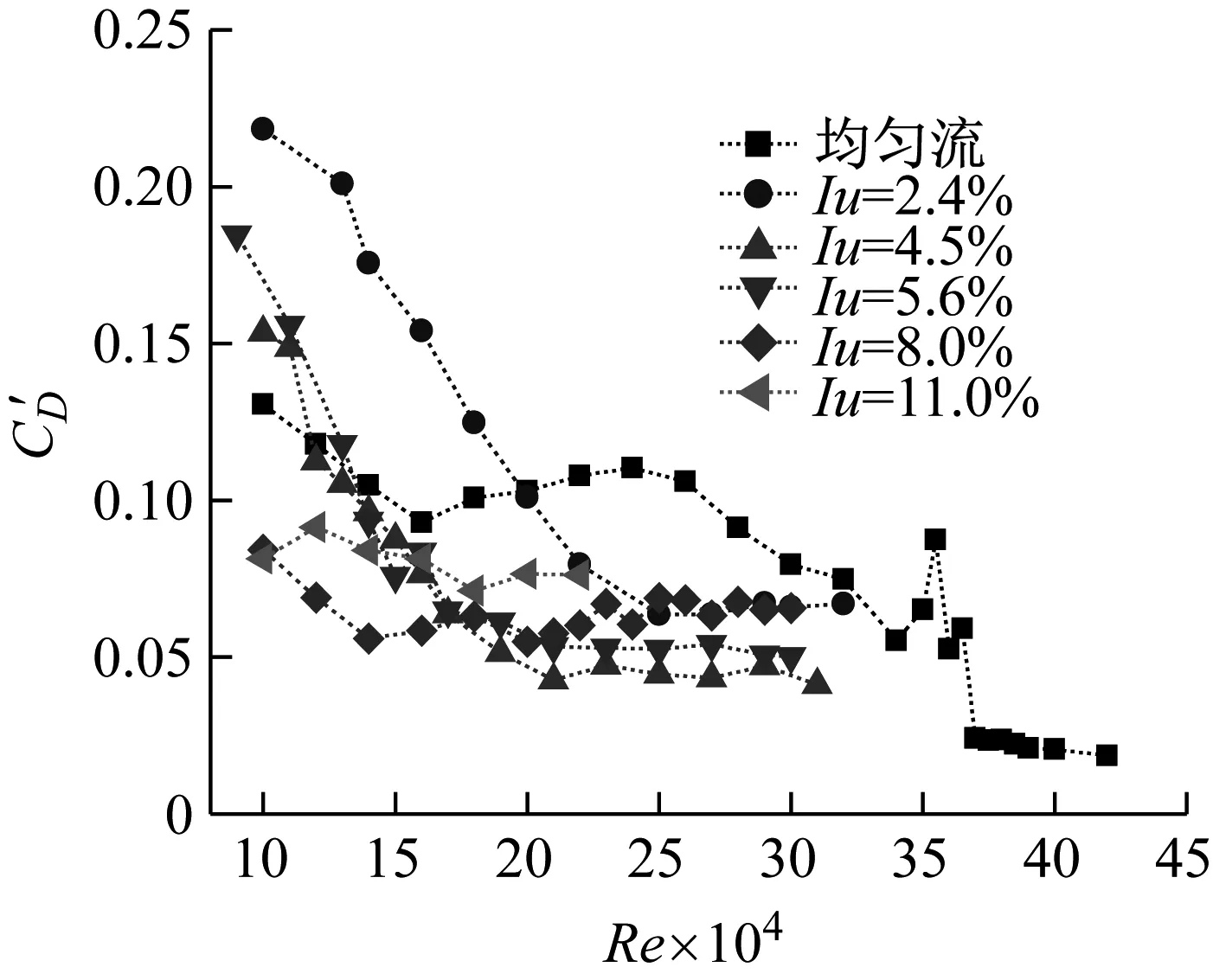
圖3 脈動阻力系數曲線

由圖3可以看出，湍流度對斜拉索的脈動阻力系數有著非常明顯的影響。當來流為均勻流的時候，在雷諾數小于3.3×105范圍內，脈動阻力系數變化幅度較小；當雷諾數在3.3×105與3.7×105之間時，脈動阻力系數出現波動，之后又迅速下降到0.05左右。當湍流度為2.4%時，脈動阻力系數在雷諾數小于2.4×105時下降幅度較大，由0.23下降到0.08左右。隨著湍流度的增加，脈動阻力系數變化幅度也相應增加，下降到最低點時對應的雷諾數也相應減小。當湍流度為4.5%時脈動阻力系數在雷諾數為8.0×104時就已經開始下降，最終下降到0.05，此時的雷諾數約為1.8×105。當湍流度繼續增加到11.0%時，在雷諾數約為1.0×105時脈動阻力系數就已經下降到最低。

圖4和圖5分別為不同湍流度下平均升力系數與脈動升力系數隨雷諾數的變化曲線。

圖4 平均升力系數曲線

由圖4可知，湍流度不同，平均升力系數隨雷諾數變化的趨勢基本相似，均是在0附近波動。均勻流時，平均升力系數在雷諾數約為3.5×105時突然上升，對應平均阻力系數突然大幅度下降的階段；而當來流有一定的湍流度時，沒有捕捉到平均升力系數突然上升的現象。

圖5 脈動升力系數曲線

圖5可以看出，湍流度對斜拉索的脈動升力系數也有著非常明顯的影響。當來流為均勻流的時候，在雷諾數小于3.3×105時，脈動升力系數變化幅度較小；當雷諾數在3.3×105與3.7×105之間時，脈動升力系數出現波動，之后又迅速下降到0.05左右。當湍流度為2.4%時，脈動升力系數在雷諾數小于2.4×105時下降幅度較大，由0.3下降到0.08左右。隨著湍流度的增加，脈動阻力系數變化幅度也相應增加，下降到最低點時對應的雷諾數也相應減小。當湍流度為4.5%時脈動阻力系數由0.45下降到0.05，此時的雷諾數約為1.8×105。當湍流度增加到11.0%時，在雷諾數約為1.0×105時脈動阻力系數就已經下降到最低。

3 平均風壓系數試驗結果分析

圖6為均勻來流時本試驗平均風壓系數與已有的試驗結果在雷諾數為1.0×105時的對比結果。通過對比發現，本試驗模型在測得的壓力系數介于顧明[19]與鄭云飛[20]之間，與Nishimura[21]和Farell[22]接近。

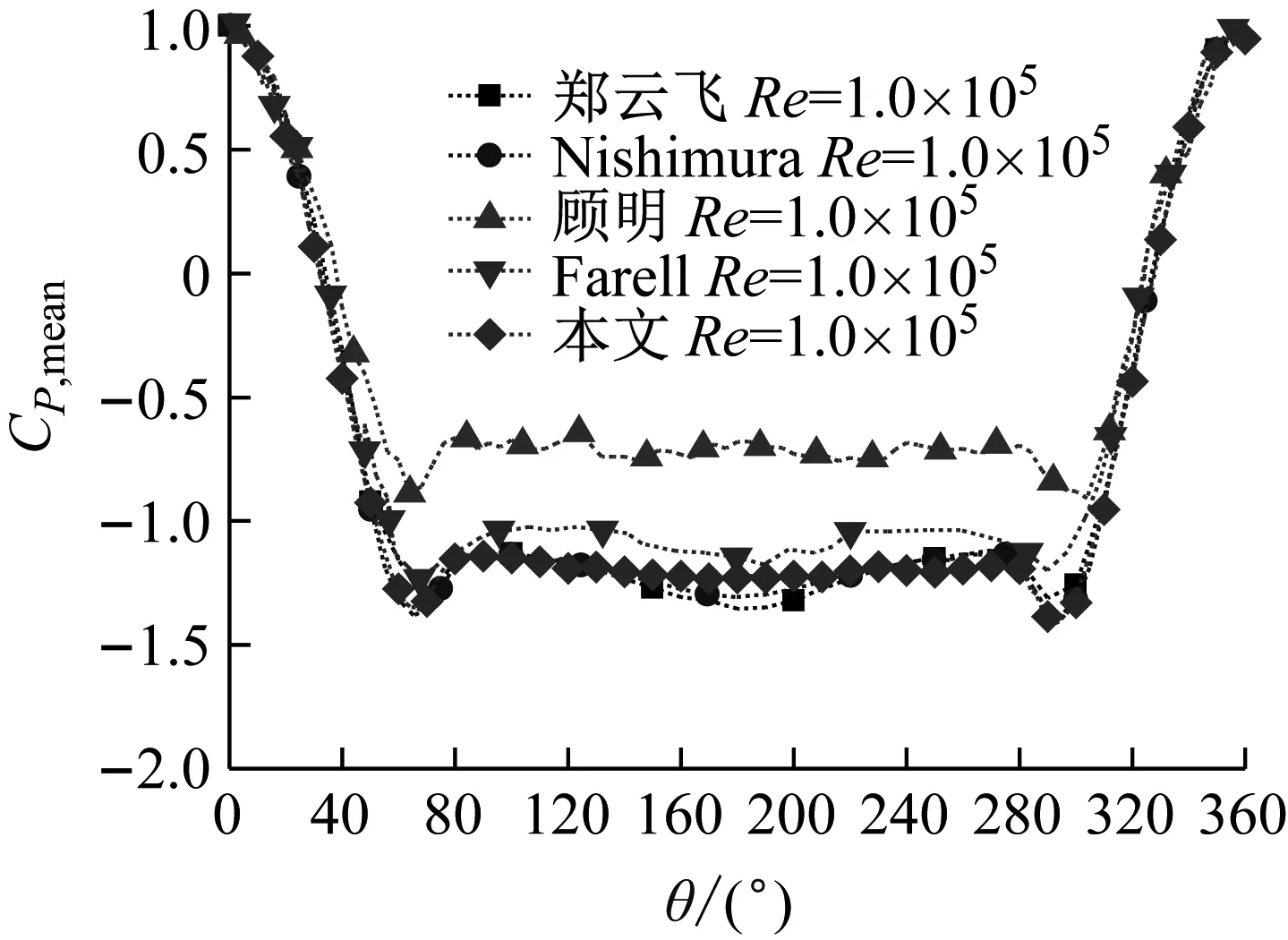
圖6 Re=1.0×105 平均風壓系數周向分布

表1為試驗條件對比，分別在模型的直徑、長度、長細比、阻塞率及雷諾數幾方面分析可能會造成圖6中差別的原因。由表1可以看到，圖6中已有的幾項研究，只有雷諾數與本文相同，而模型直徑、長度、長細比及阻塞率與本研究均不相同。因此可以總結，在雷諾數相同的條件下，模型直徑、長度、長細比、阻塞率等參數都會對模型的壓力系數產生一定的影響，造成了平均風壓系數有略微的差別，但是差別并不是很明顯。

表1 不同模型參數

圖7顯示了不同湍流度下的不同雷諾數時的平均壓力系數的周向分布規律。由圖7可見，每個湍流度下平均風壓系數的周向分布規律基本相同，平均風壓系數呈現出對稱分布。隨著角度的增加平均風壓系數下降，直到下降到分離點達到最大平均負風壓。分離點之后平均分壓系數開始上升，在背風面區域平均風壓系數基本保持不變。隨著雷諾數的增加，各個湍流度下分離點處的最大平均負風壓系數向下移動。

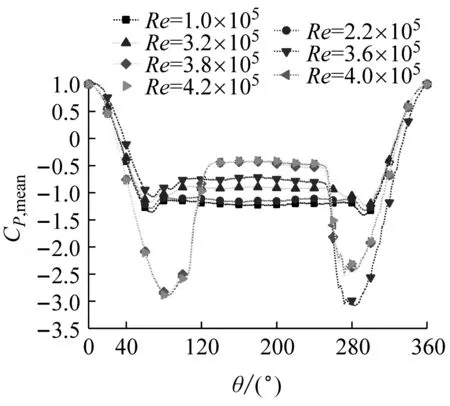
(a) 均勻流時平均風壓系數

(b) Iu=2.4%平均風壓系數

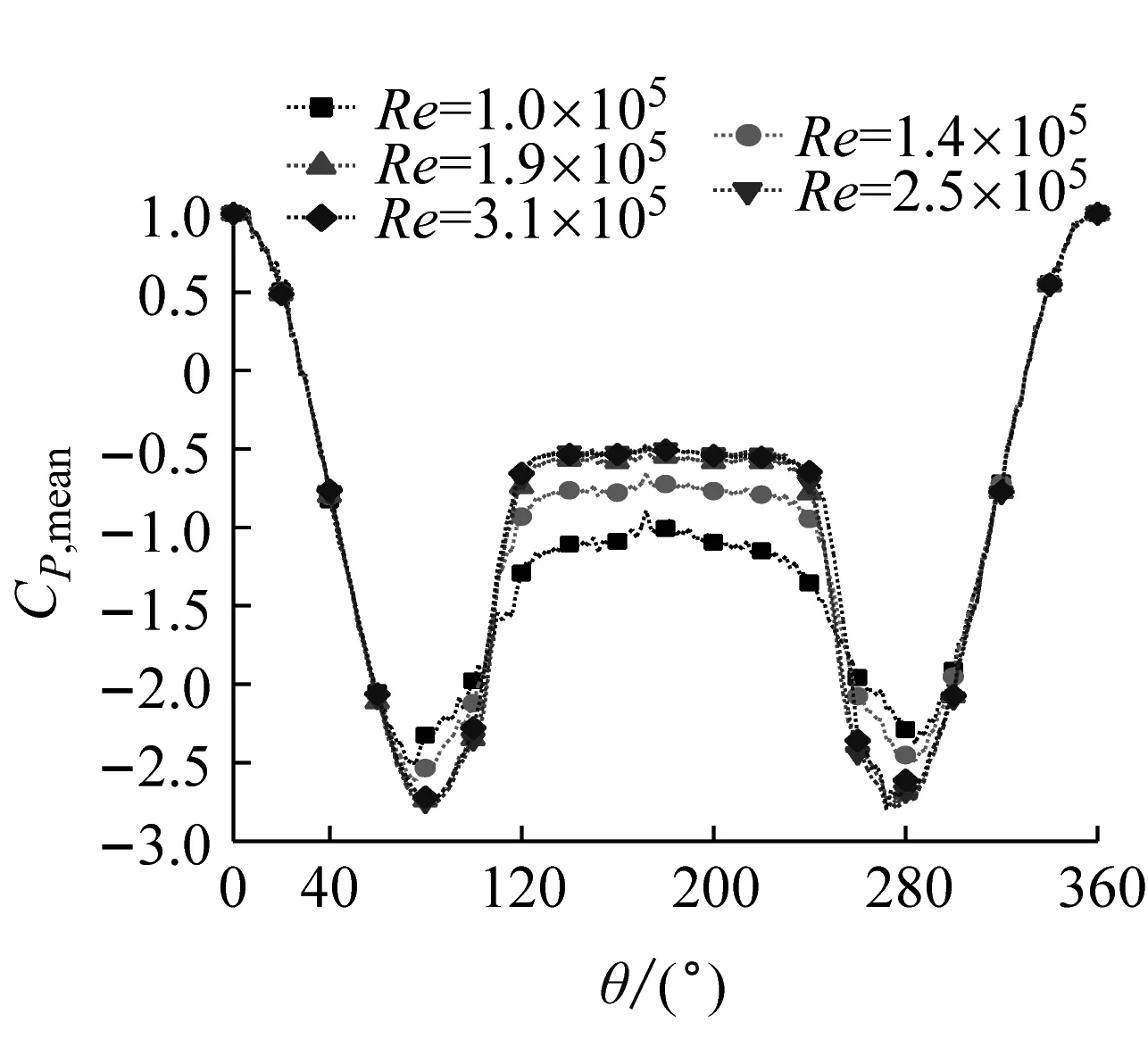
(c) Iu=4.5%平均風壓系數

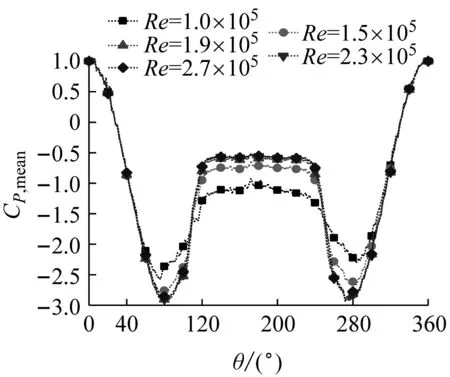
(d) Iu=5.6%平均風壓系數

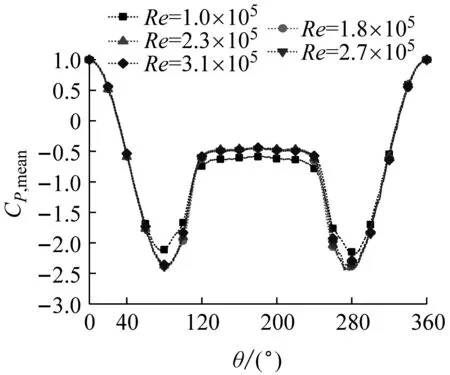
(e) Iu=8.0%平均風壓系數

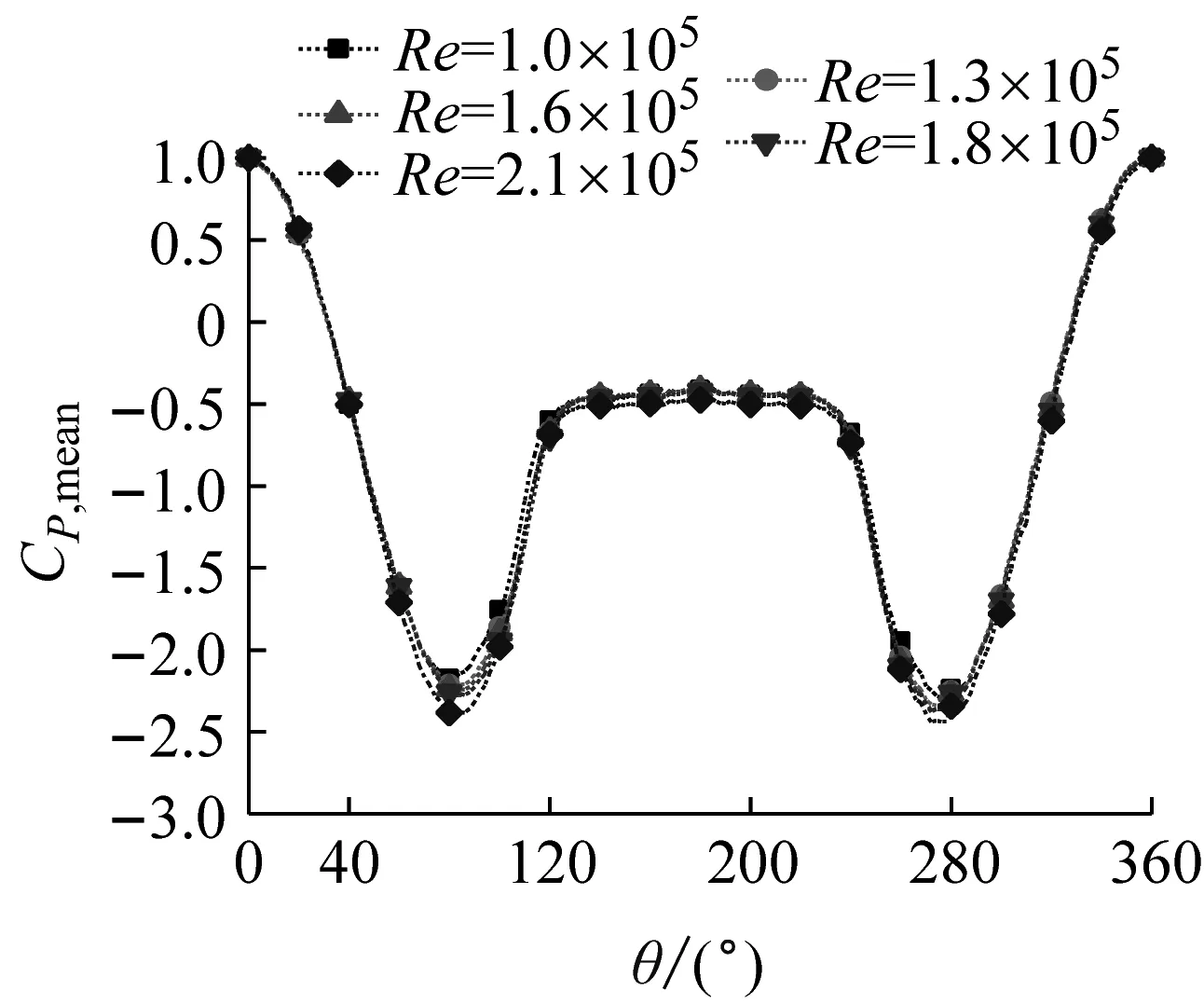
(f) Iu=11.0%平均風壓系數

對比不同湍流度下的變化曲線發現，湍流度越大，平均風壓系數越接近；而湍流度較小時，平均風壓分布曲線相差越多。由以上對比還可以發現當雷諾數相同時，分離點處的平均風壓系數向下移動，而尾流區也會逐漸變窄。

為了更方便觀察此現象，選取了幾個較為有代表性的雷諾數，對比分析相同雷諾數下平均壓力系數周向分布隨湍流度的變化規律，如圖8所示，選取圖8中豎線穿過的雷諾數區域作為研究對象，雷諾數分別為1.0×105、1.6×105和2.7×105，Re=1.0×105是每個湍流度工況均含有的最小的雷諾數，Re=1.6×105時大部分湍流度工況下的平均阻力系數處于急速下降狀態，Re=2.7×105時則是平均阻力系數處于平穩的狀態。不同湍流度下平均壓力系數周向分布隨湍流度的變化規律,如圖9所示。

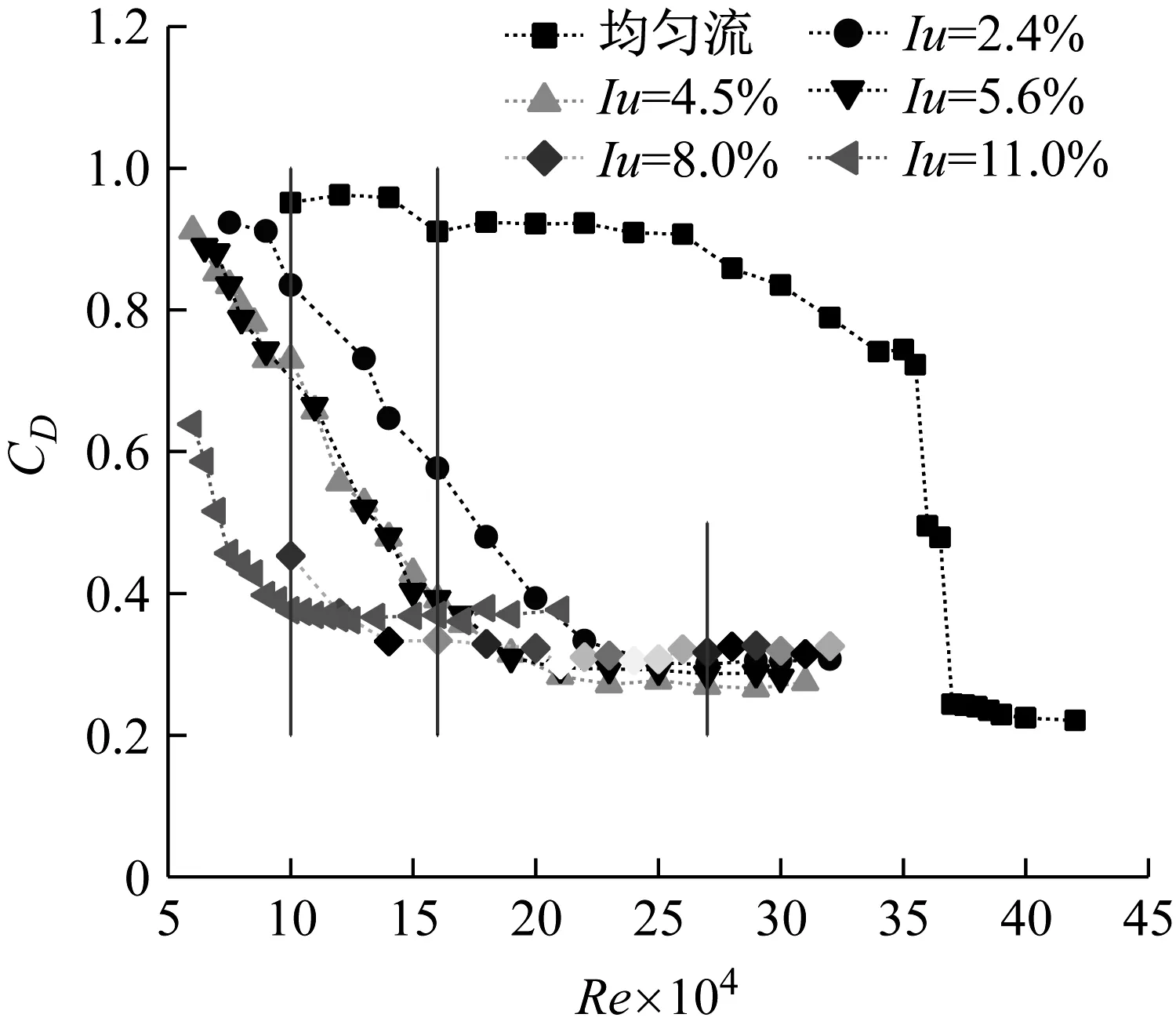
圖8 平均阻力系數曲線

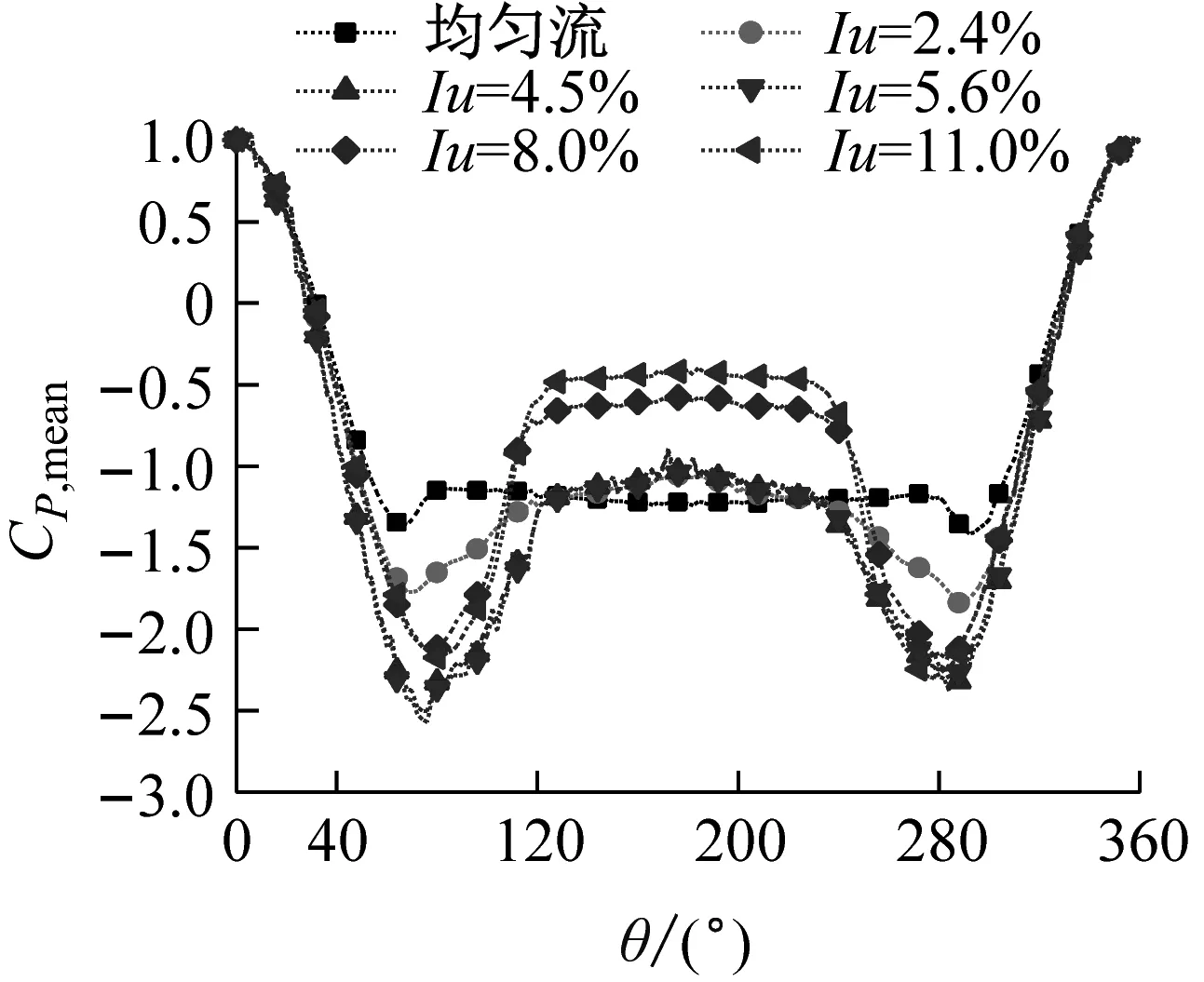
(a) Re=105平均壓力系數

(b) Re=1.6×105平均壓力系數

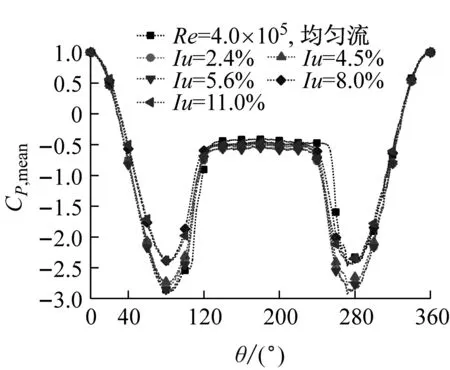
(c) Re=2.7×105平均風壓系數

圖9 平均風壓系數周向分布

Fig.9 Circumferential distribution of average wind pressure coefficient

4 脈動風壓系數的試驗結果分析

圖10為同一湍流度下不同雷諾數時的脈動壓力系數周向分布情況。

由圖10可見，每個湍流度下的脈動風壓系數的周向分布規律基本相同，整體呈對稱分布，并且隨著角度的增加，脈動風壓系數增加，在分離點處出現峰值，之后隨著角度的增加脈動風壓系數減小，在背風面脈動風壓系數變化較小。當雷諾數較小時，壓力系數峰值處會出現駝峰現象，但是隨著雷諾數的增大，駝峰現象減弱。均勻流時背風面壓力的上下波動為較為頻繁的駝峰。在雷諾數較低時，斜拉索尾流區的脈動風壓系數的變化出現尖點現象，但是當雷諾數增大時，尾流區的脈動風壓系數逐漸趨向平緩。

對比圖10(a)～(f)得出，湍流度較低時，脈動風壓系數的駝峰現象較為明顯，而隨著雷諾數的增加此現象有所減弱直到消失。隨湍流度增加，脈動風壓系數有增大的趨勢。

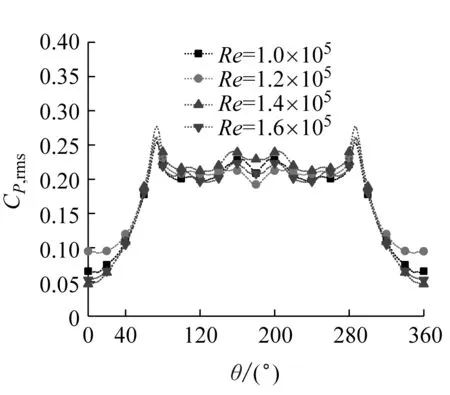
(a) 均勻流時脈動風壓系數

(b) Iu=2.4%脈動風壓系數

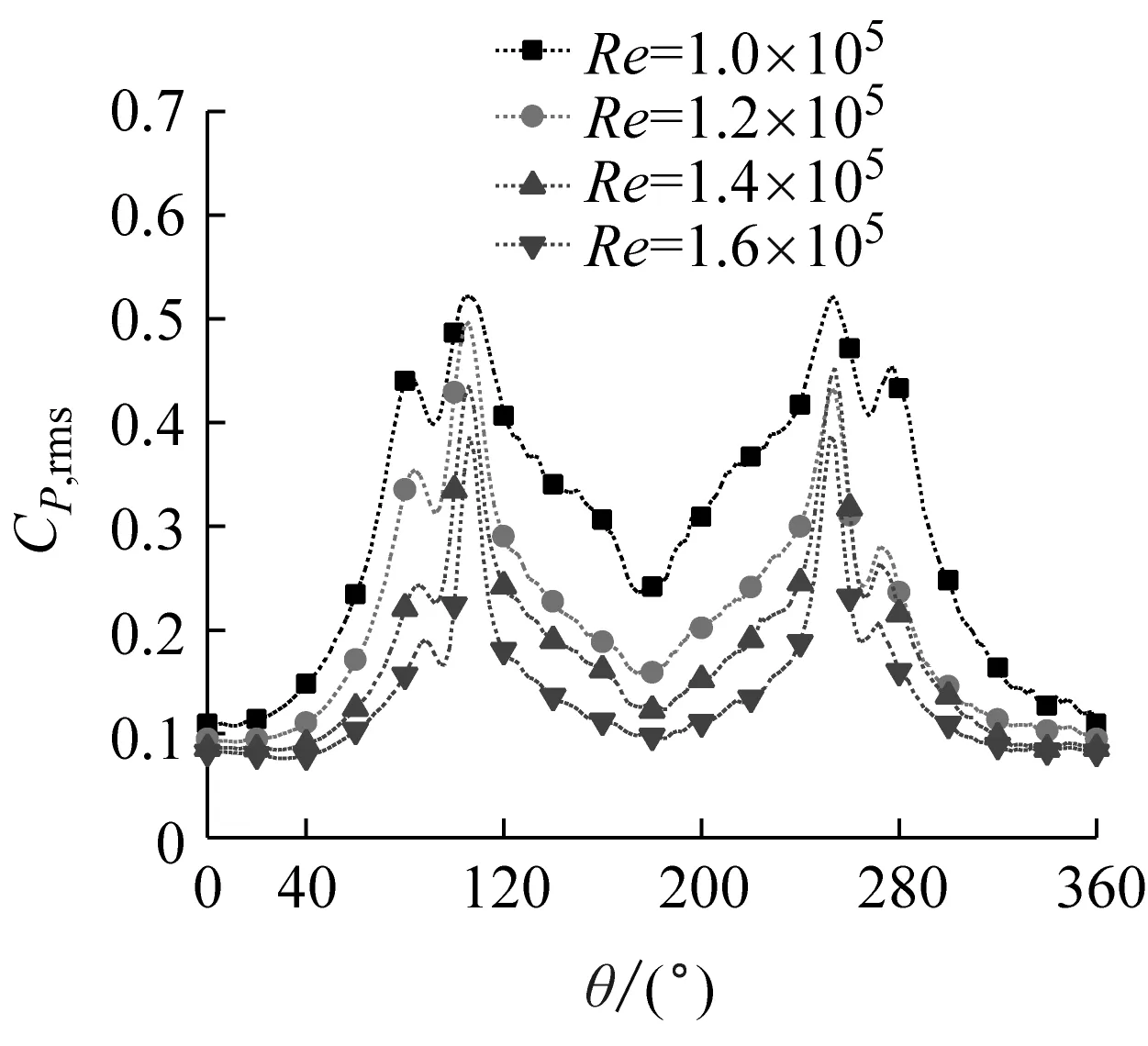
(c) Iu=4.5%脈動風壓系數

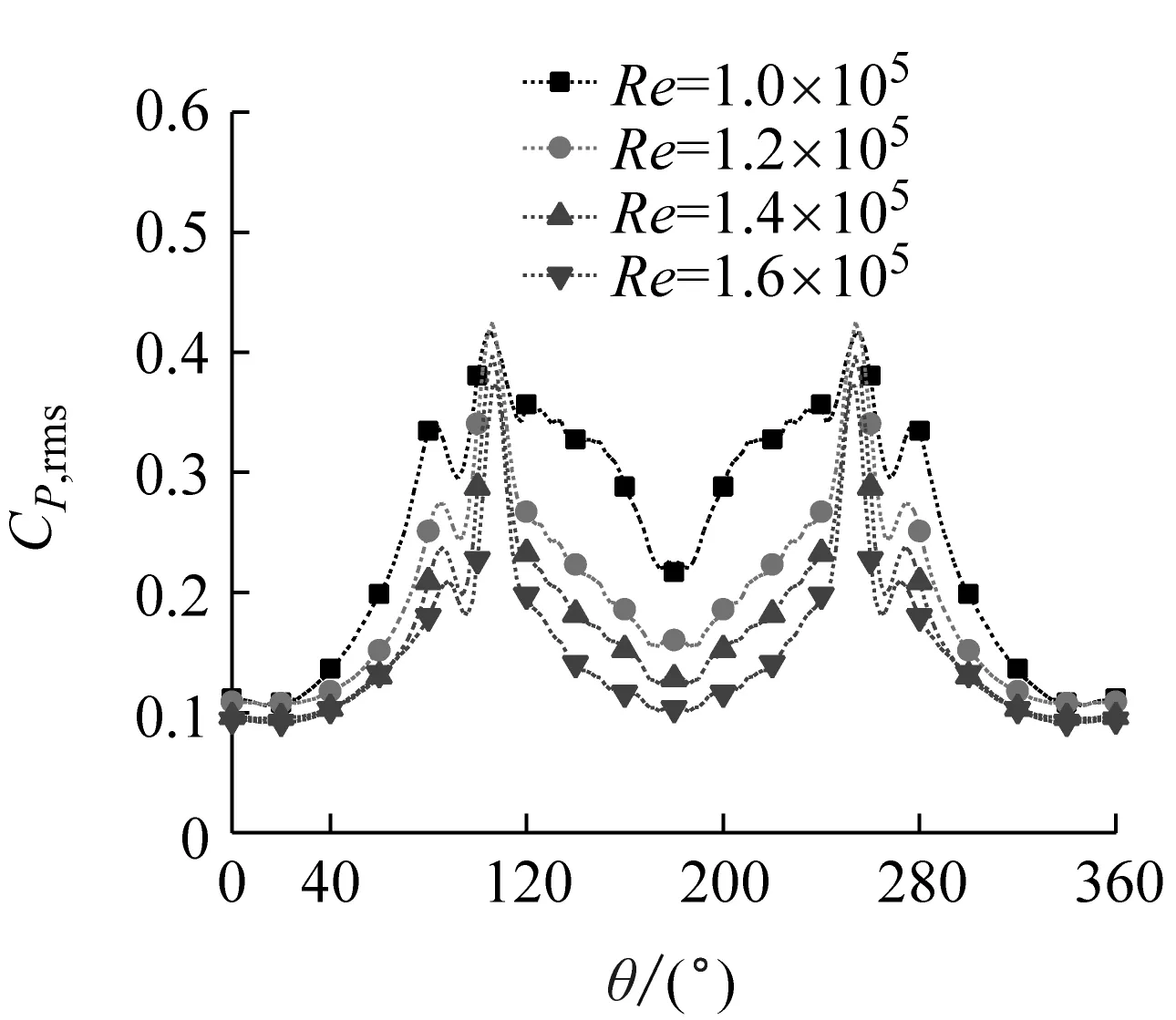
(d) Iu=5.6%脈動風壓系數

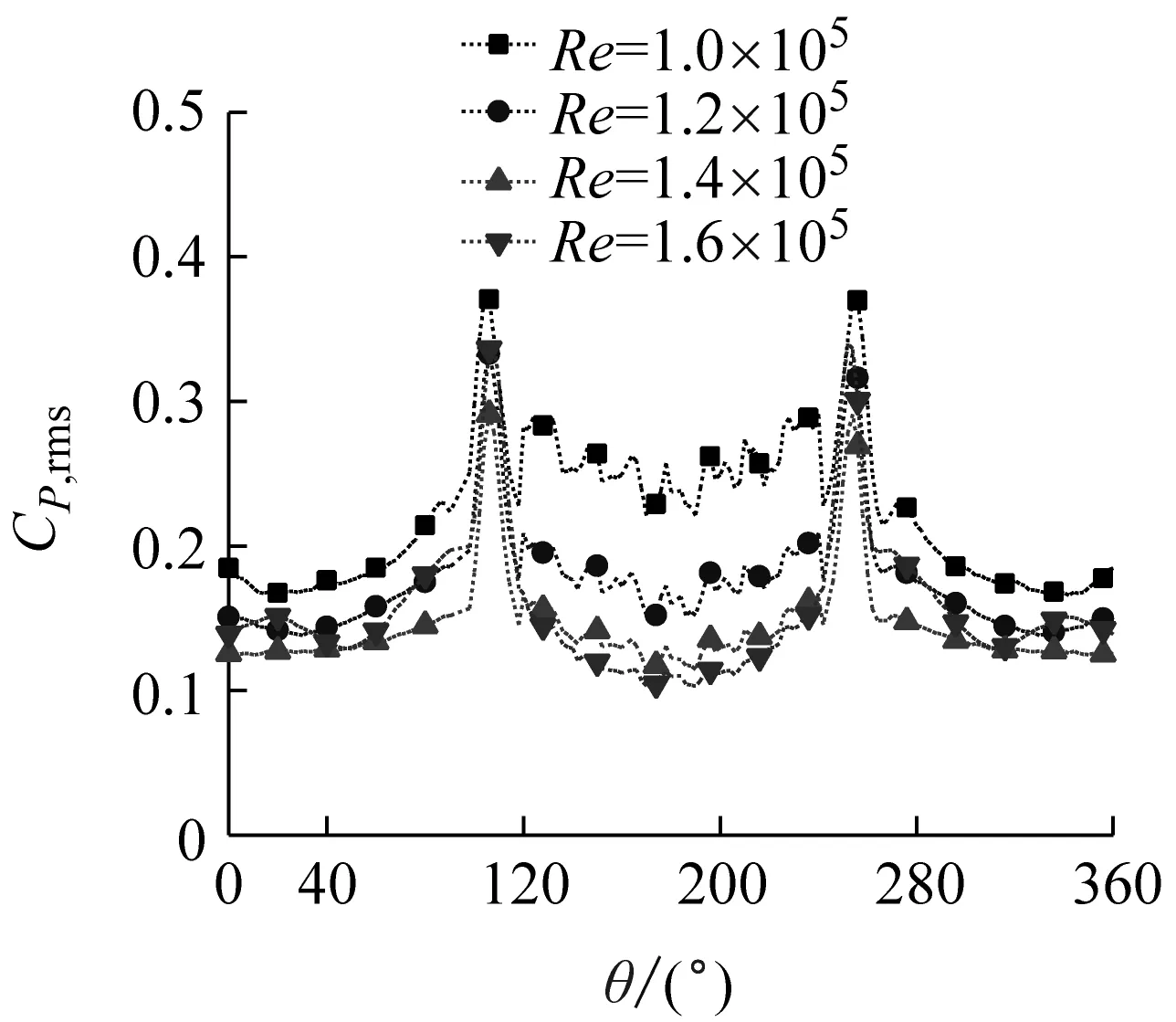
(e) Iu=8.0%脈動風壓系數

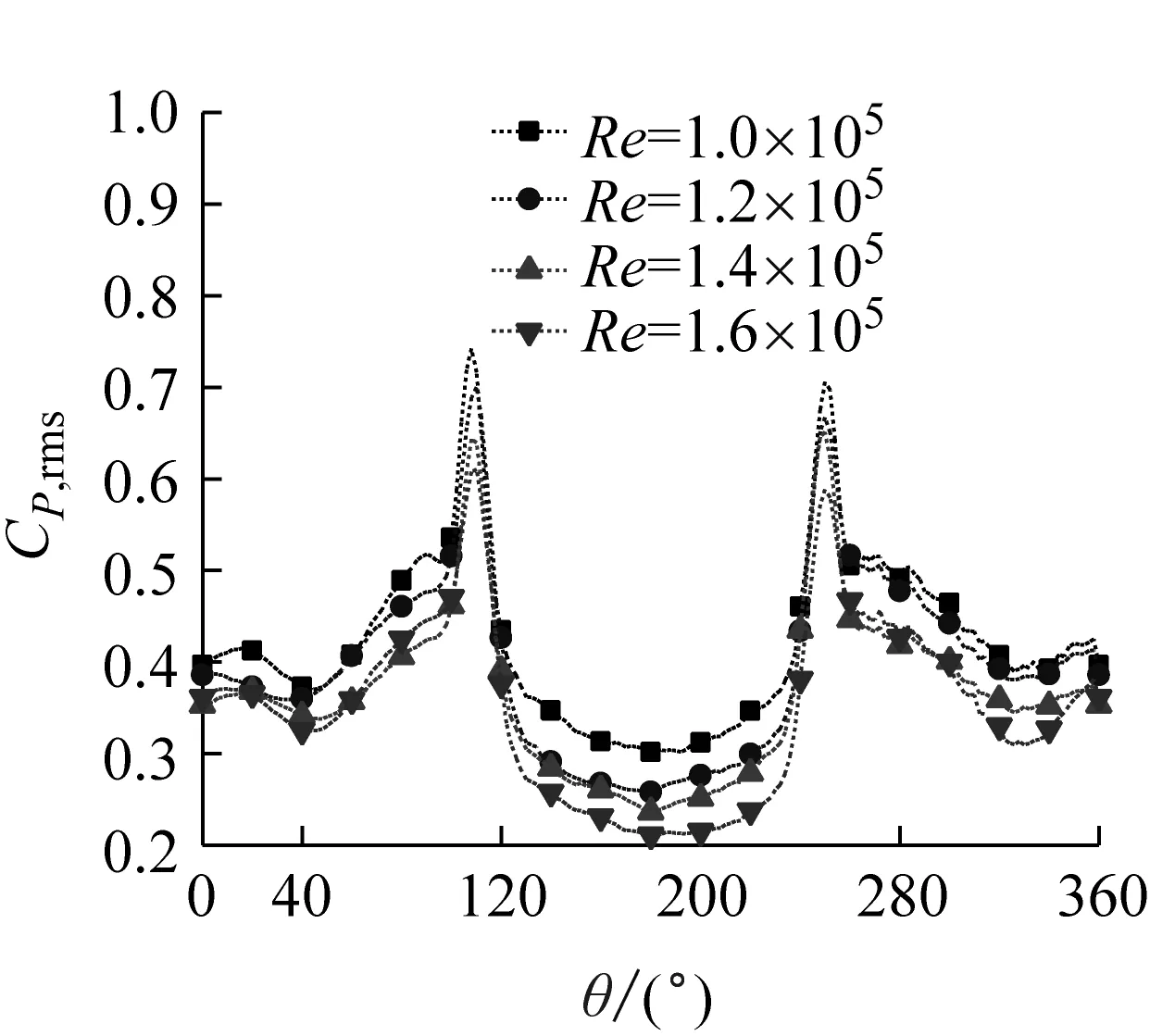
(f) Iu=11.0%脈動風壓系數

為了更方便對比，下文選取了三種不同的雷諾數工況，圖11為雷諾數是1.0×105、1.6×105和2.7×105時不同湍流度下的脈動風壓系數。由圖可以看出，當湍流度較低時，脈動風壓系數的變化會出現駝峰現象，此現象會隨著湍流度的增加或者雷諾數的增大而減弱；湍流度增加，不同雷諾數下的脈動風壓系數均會增加。同時，湍流度在小于5.6%時脈動風壓系數隨湍流度增加而增加，但是變化幅度不是很大。當湍流度在8.0%到11.0%之間時，脈動風壓系數出現大幅度上升，可見湍流度越大，脈動風壓越不穩定。

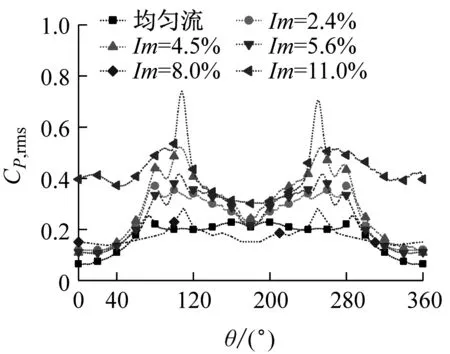
(a) Re=105脈動風壓系數

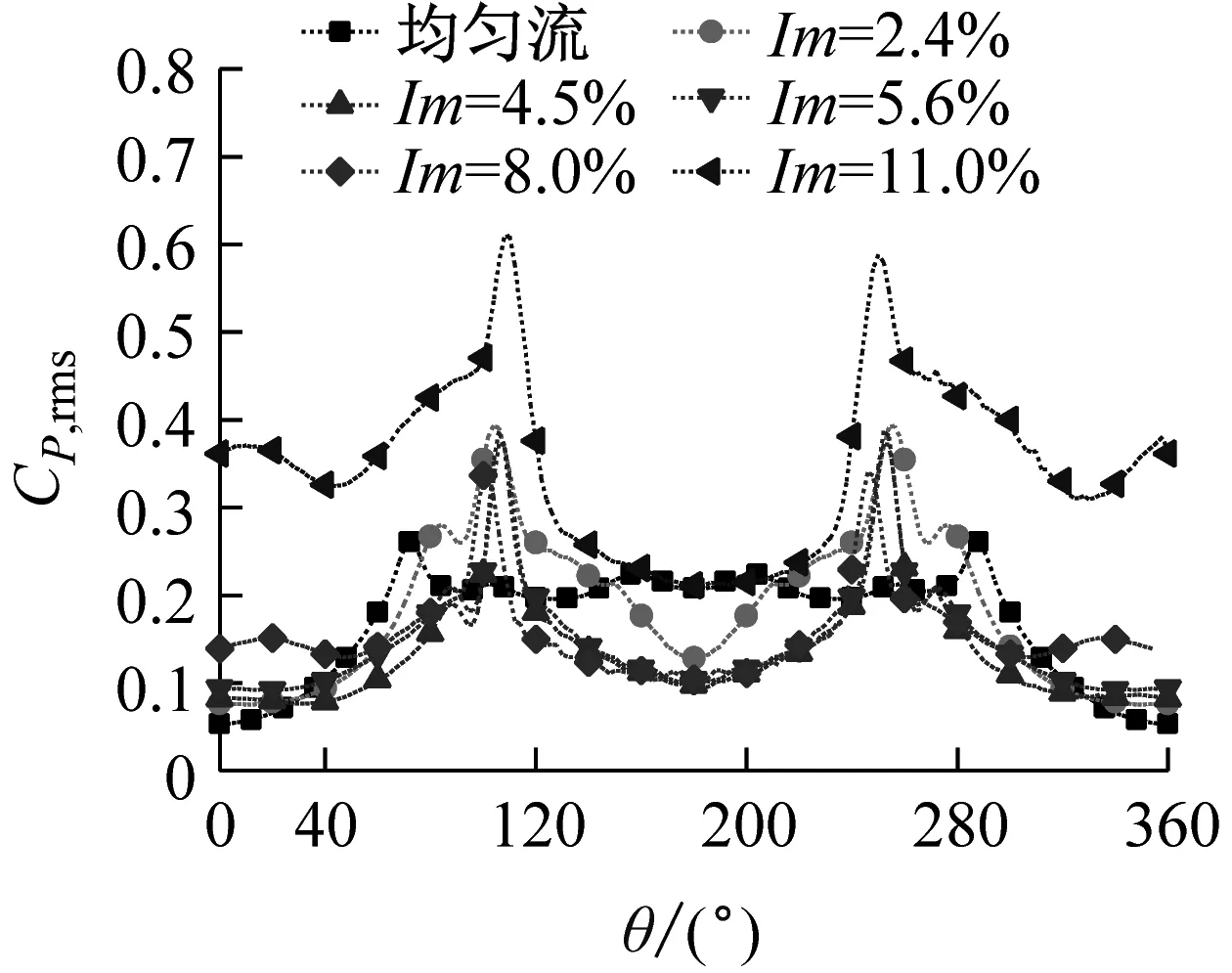
(b) Re=1.6×105脈動風壓系數

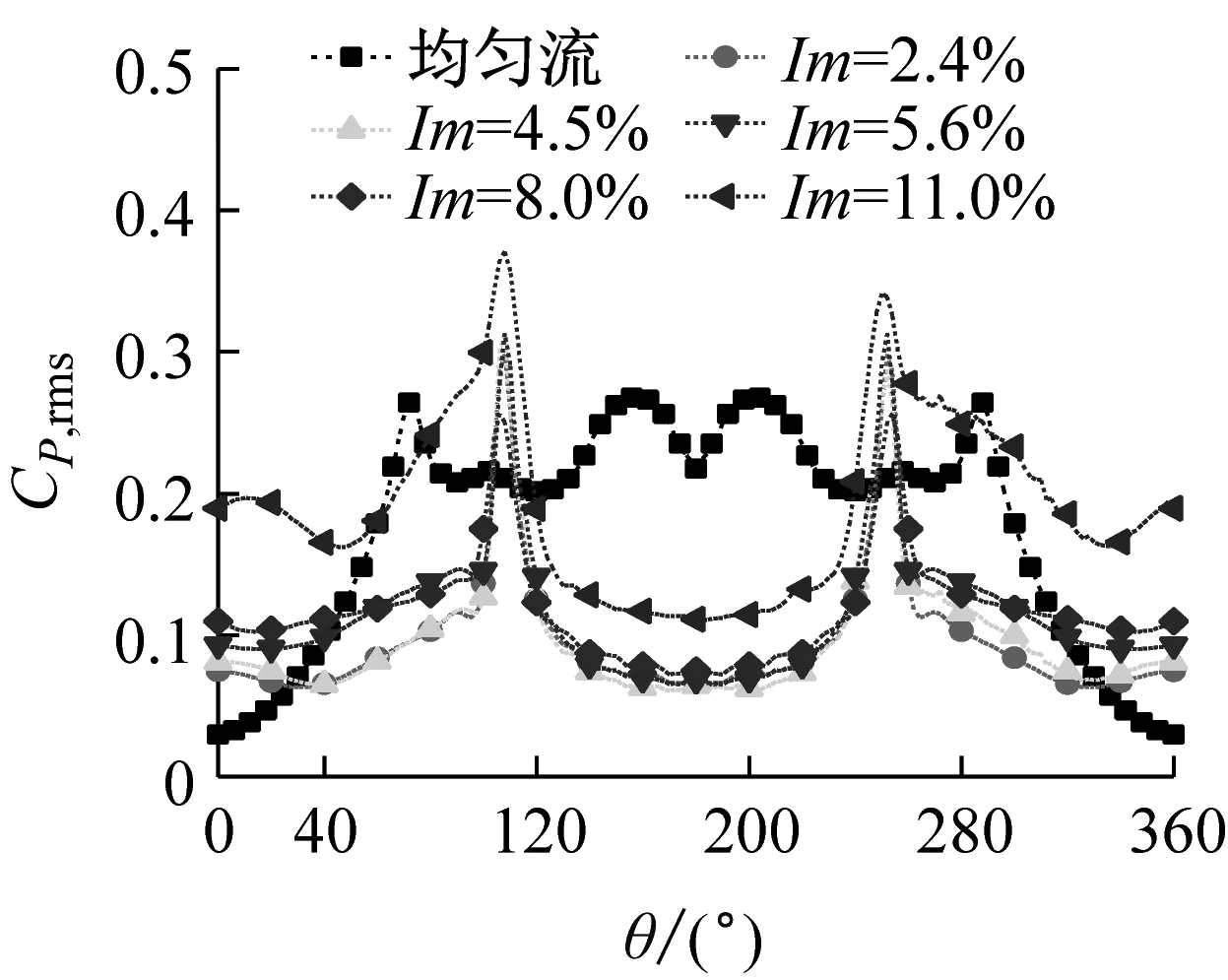
(c) Re=2.1×105脈動風壓系數

圖12為不同雷諾數下的迎風面測點脈動風壓系數隨湍流度的變化曲線。

圖12 迎風面測點脈動風壓系數曲線

由圖12可以看出，隨著湍流度增加，每一個雷諾數下的迎風面測點脈動風壓系數增大；隨著雷諾數增大，每個湍流度工況下的迎風面測點脈動壓力系數減小。

5 結 論

本文采用風洞試驗測壓的方法，充分考慮實際斜拉索所處的真實湍流環境，對不同湍流度下的光滑斜拉索氣動力特性進行了試驗研究，得到以下結論：

(1) 湍流度的存在使得斜拉索氣動參數的雷諾數效應提前，湍流度越大，雷諾數效應提前的越明顯。即湍流度越大，斜拉索的平均阻力系數、脈動阻力系數及脈動升力系數開始迅速下降及下降到最低點時對應的雷諾數越小。

(2) 不同湍流度下斜拉索的平均風壓系數周向分布規律基本相同，但湍流度越大，不同湍流度的平均風壓系數周向分布曲線越接近。同時，湍流度對平均風壓系數的影響也受到雷諾數的制約，雷諾數較小時，湍流度對斜拉索平均風壓系數的影響較大，而當雷諾數增大到一定程度時，湍流度的影響不再明顯。

(3) 隨著來流湍流度的增加，斜拉索的平均風壓系數及脈動風壓系數一般會增大。試驗發現，當湍流度較小時，斜拉索脈動風壓系數在背風面會出現較為明顯的駝峰現象，而湍流度增大，此現象逐漸減弱直至消失。