基于超幾何函數和梅哲G函數的變截面梁的非線性振動建模及自由振動

薄 喆，葛 根

(天津工業大學 機械工程學院，天津 300387)

變截面懸臂梁在眾多結構中有廣泛應用,如微機電系統中的光電開關,壓電能量收集器[1],原子力顯微鏡[2]等。其振動特性是近20年研究的重點。對于小振幅的線性振動,變截面懸臂梁的特征頻率和振型函數的確定是一大難點。對于大振幅的振動，其非線性特性對梁的工況有極大的影響，研究者需要度量振動的非線性的性質(漸軟或漸硬)及得到較精確的幅頻響應關系。

由于控制梁線性振動的偏微分方程形式沒有簡單函數解，振型函數的研究主要有四種方向。①假設截面隨梁長慢變,采用攝動法的思想,在均勻截面梁的振型函數的基礎上攝動,從而得到新的頻率。顯然這種方法理論推導計算較繁瑣[3]。②采用瑞利-里茲法，采用滿足邊界條件和正交性條件的試驗振型函數，不斷修改項數，直到得到的頻率收斂。由于該方法需要不斷選擇試驗函數，又要增加項數，所以非常耗費機時[4-5]。③基于有限元的半解析法，這種方法是先用有限元建模，得到振型圖像后，用多項式函數進行逼近，然后用該多項式函數當成振型函數進行計算[6-7],因此有較大的舍入誤差。④稱為特殊函數法，通過變量變形，將方程的解設為特殊函數，如貝塞爾函數[8-9]、超幾何函數[10-11]、梅哲G函數[12-13]的形式。該種方式的缺點在于振型函數表達式對工程人員而言晦澀難懂，有時振型函數的系數可能是復數，導致畫振型圖不便，其優點在于精確度高，因為它沒有經過任何的近似逼近。

對于大振幅下的非線性特性，主要關注點在于彎曲導致的幾何非線性和軸向橫向位移關聯導致的慣性非線性。這兩種非線性項系數一般來自對變截面梁的偏微分方程的伽遼金法。得到幾何非線性系數和慣性非線性系數之后，需要對整體非線性的性質進行度量(漸硬或漸軟)。在均勻截面和變截面的懸臂梁研究中，多尺度法都被用以獲取系統的幅頻響應及度量漸軟或漸硬特性的有效非線性系數。

針對以上的研究現狀。本文的工作如下：①首先用凱恩方程對一個均勻厚度，從固定端向自由端沿軸線逐漸收窄的懸臂梁動力學建模，建模過程中已經考慮幾何非線性和慣性非線性。相比于原來的先用偏微分后伽遼金截斷的方法，此方法得到的幾何非線性系數和慣性非線性系數表達式更加簡潔。②對模型的線性部分直接求解模態函數，在計算軟件的幫助下，本文采用超幾何函數和梅哲G函數的線性組合可保證解的準確度，振型頻率和有限元法結果、瑞利里茲法結果對比后，高度一致。代入幾何非線性系數和慣性非線性系數表達式后，發現結果和原來的伽遼金方法結果完全一致，從而驗證了本文方法的正確性。③對系統非線性特性的研究沒有使用廣為人知的多尺度法，因為眾所周知多尺度法的適用范圍是弱非線性振動。本文采用了更適用于強非線性振動的變分法和能量平衡法，并在能量平衡法的基礎上加以改進得到了相圖近似效果更好的結果。并且基于這些結果得到了有效非線性系數。

1 動力學建模過程

如圖1所示，假設該歐拉伯努利梁為沿著軸線漸窄的等厚度懸臂梁，其特征為：長度L，固定邊的寬度b0，自由端的寬度為bl，厚度為h，楊氏彈性模量為E，密度為ρ。沿軸向建立軸線坐標s，梁的微段長度為ds，橫向位移w(s,t)和軸向位移u(s,t)。重力效果忽略不計。

1.1 凱恩方程

(1)

(2)

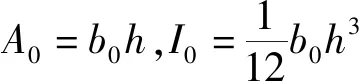
該懸臂梁假設為金屬的不可伸長，如圖1(b)所示，橫向位移w(s,t)和水平位移u(s,t)的關系如下:

(3)

式中：ξ為形式變量.梁的變形可表示為:

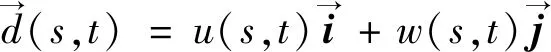
(4)

(5)

(6)

式中：(·)表示對時間t求偏導。梁的彎矩M和彎曲變形能U表示為:

(7)

(8)

式中：(′)表示對s的偏導數。 把式(7)代入式(8),最終的彎曲變形能為：

(9)

假設第i階梁的模態方程為：

wi(s,t)=φi(s)qi(t)

(10)

式中：φi(s)為暫時未知的模態空間分布函數。在自由振動假設下，本文不考慮內共振的影響。

將式(10)代入式(5)、(6)和(9)后，再統一代入凱恩方程：

(11)

(12)

引入無量綱變化關系：

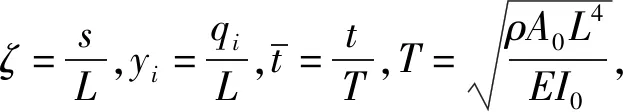
(13)

1.2 基于超幾何函數和梅哲G函數的振型

接下來我們需要確定振型函數φ，由線性振動的常厚度、線性變寬度的懸臂梁偏微分振動方程可知：

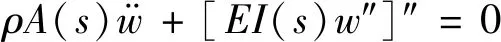
(14)

邊界條件為:

w(0,t)=0,w′(0,t)=0,

EI(s)w″(s,t)|s-L=0,[EI(s)w″(s,t)]′|s-L=0

(15)

采用上述相同的無量綱變換，將式(10)代入式(14)可得：

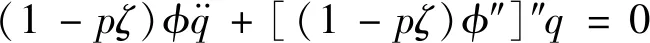
(16)

(1-pζ)φβ4-[(1-pζ)φ″]″=0

(1-pζ)φ″|ζ=1=0,[(1-pζ)φ″]′|ζ=1=0

(17)

對于常截面懸臂梁(p=0)模態方程為眾所周知的：

φ(ζ)=cosh(βζ)-cos(βζ)+

(18)

式中：β是特征方程式(19)的根

1+cos(β)cosh(β)=0

(19)

但是，對于本文研究的變截面梁而言，模態方程沒有如此簡單。本文對式(17)直接求解，可得一組由超幾何函數和梅哲-G函數線性組合而成的基函數[12-13]:

φi(ζ)=C1iφ1i+C2iφ2i+C3iφ3i+C4iφ4i,

i=1,2,3,4

(20)

式中：Ci為待定系數。

(21)

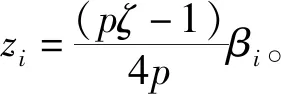
超幾何函數pFq和梅哲G函數的定義如下：

pFq(a1,a2…ap;b1,b2…bq;z)=

(22)

(23)

式(22)、(23)中z為獨立自變量,a1-ap和b1-bq為實常數。在式(23)中η為一個復變量,m,n,p,q為滿足0≤m≤q,0≤n≤p,的整數，Γ()表示歐拉Gamma函數。關于超幾何函數pFq和梅哲G函數的數學性質及相互關系不在本文贅述，可參考數學工具手冊。事實上用數學軟件Mathematica或Maple都可實現從式(17)中第一個等式直接求解出式(20)的過程。

為確定待定系數Ci和βi，需考慮式(17)后的四個邊界條件。

(24)

1.3 常微分振動方程的系數確定

有了φi(ζ)函數，常微分方程式(13)可以重新寫為

(25)

式中系數含義為:無量綱固有頻率ωi,無量綱彎曲幾何非線性系數α1i,無量綱慣性非線性系數α2i。

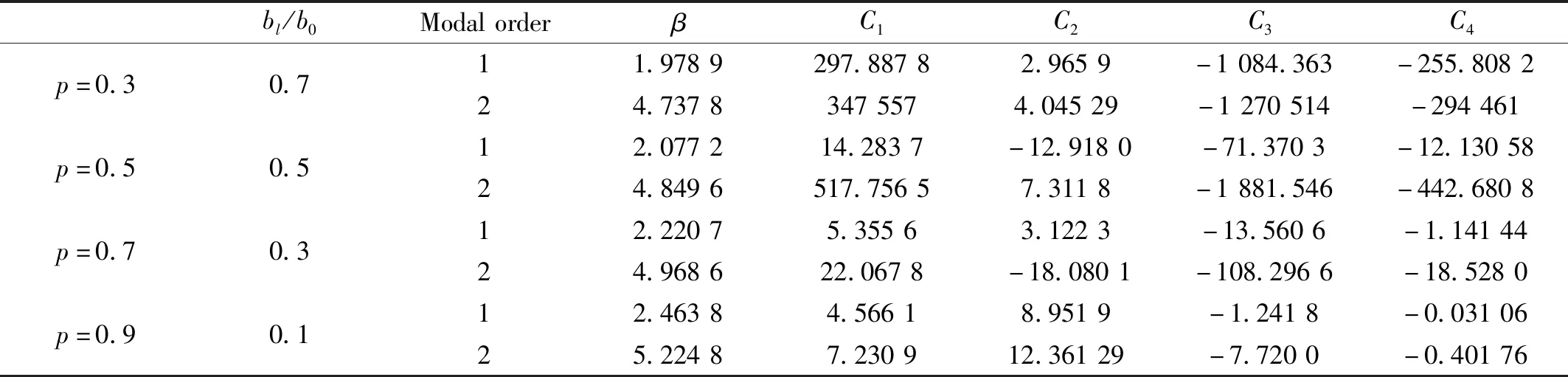
表1 前兩階模態的系數Ci和βi

(a) 第一階模態

(b) 第二階模態

(26)

由以往的文獻中對于均勻截面懸臂梁的研究而眾所周知的結論：幾何非線性系數α1i決定了方程的漸硬特性，而慣性非線性系數α2i決定了方程的漸軟特性，我們需要研究不同的形狀參數p對這兩個系數的影響結果。

在計算式(26)之前，需要驗證本文的推導過程的正確性，可將文獻[14]中由牛頓微元法推導出來的模型進行對比。其文中的動力學偏微分控制方程：

(27)

采用上文相同的無量綱化可得：

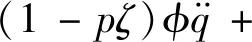
w(0,t)=0,w′(0,t)=0,

(1-pζ)w″(1,t)=0,[(1-pζ)w″(1,t)]′=0

(28)

用伽遼金法對各項乘以φ再對ζ沿著梁長從 0 到 1積分，則各系數可得：

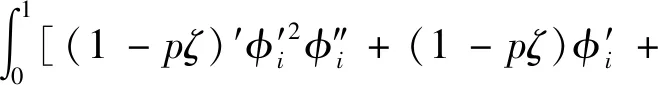
(29)

比較式(26)和式(29)可知，各系數的表達形式完全不同，本文方法得出的式(26)比式(29)更加簡短。但是如果將式(20)連帶表1的各系數分別代入式(26)和式(29)，前兩階振型的系數計算值是完全相同的。結果如表2所示。這就證明了本文建模方法的正確性。

由表2可知，隨著懸臂梁的自由端逐漸收尖，前兩階振型的自由振動的固有頻率、幾何非線性系數和慣性非線性系數都在逐漸增大。本文方法得到的線性固有頻率的值可以和文獻[14]中的有限元方法、及瑞利-里茲法得到的結果進行對比。

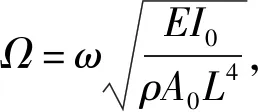
表2 前兩階模態的方程系數

表3 不同方法得到的圓頻率rad/s的比較

Tab.3 Comparison of the frequency (rad/s) obtained by different methods

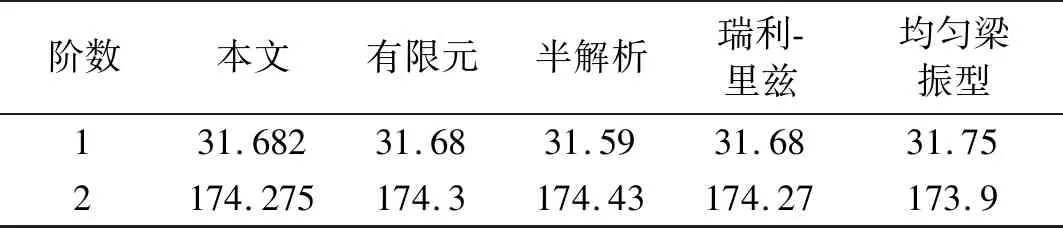
階數本文有限元半解析瑞利-里茲均勻梁振型131.68231.6831.5931.6831.752174.275174.3174.43174.27173.9

從表3來看，本文方法和里茲-瑞利法還有有限元直接模擬法最一致，直接用均勻截面梁振型的方法精度最低，半解析法精度優于直接用均勻截面的振型，低于其他方法，原因可能是曲線擬合時的舍入誤差。接下來我們研究方程的漸硬或漸軟特性。

在文獻[15]研究中，作者們用多尺度法得出了一個判斷系統究竟是漸硬還是漸軟特性的參數，稱為有效非線性系數：

(30)

當δi>0說明i階振型呈現漸硬特性，反之，呈現漸軟特性。本文也要研究隨著截面形狀參數p的變大，系統的有效非線性系數將如何變化。

文獻[14-15]采用的研究方法為多尺度法，是適用于弱非線性振動的有效方法，但是如果振幅較大、非線性較強時，求解的頻率精度略有不足，目前不知用式(30)表示的有效非線性系數判斷漸硬漸軟特性是否合理。所以需要更精確的方法求得響應頻率，進而進一步研究有效非線性系數的合理性。

2 求解響應幅頻關系及有效非線性系數

處理含有非線性項的振動方法非常多，有基于攝動思想的多尺度法、平均法等，它們一般適用于弱非線性振動。基于系統哈密爾頓函數能量的變分法，和能量平衡法等，既可以適用于弱非線性也適用于強非線性。本文采用變分法[16]和能量平衡法(EBM)[17]兩種方法來研究振動的幅頻關系，因為其計算過程相比攝動法簡單易操作而且精度較高。

2.1 變分法

假設式(25)的初值條件為：

(31)

式(25)的變分方程為：

(32)

假設近似解的形式為：

y=Acos(θ)，θ=ω10t

(33)

式中的ω10為待定的響應頻率，A為振幅。將式(33)代入式(32)，可得：

(34)

需要保證J(y)對不同的A保持不變，因此需要J(y)對A求偏導數等于零。

(35)

可解得：

(36)

2.2 能量平衡法及改進

式(25)的哈密爾頓能量為：

(37)

將近似解式(33)代入式(37)后，得：

(38)

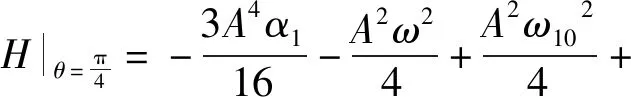
(39)

(40)

令這兩個值H1、H2相等可解得：

(41)

可見式(36)和式(41)完全一致，它們和由多尺度法得出的結果[18]式(42)略有不同。

(42)

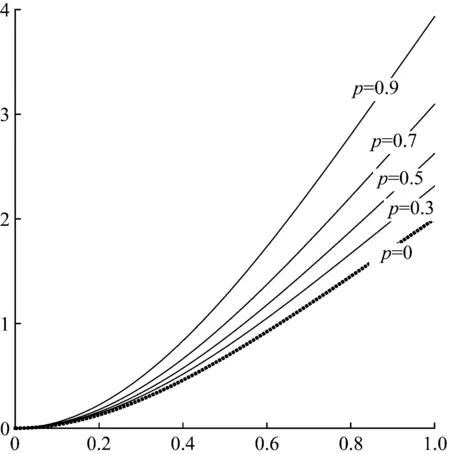
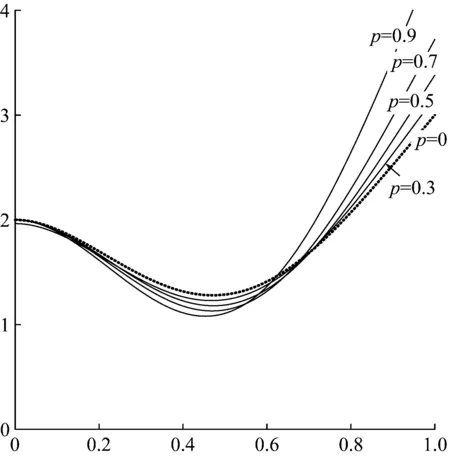
圖3為對一階振型的數值模擬的結果，實線為龍格庫塔法結果、散點線為能量平衡法結果、點劃線為多尺度法結果。在振幅較小時，兩類方法的結果很接近，如圖3(a)、(b)所示，其中我們選擇p=0.7，振幅為A=0.05。雖然多尺度法不如能量平衡法的結果精確，但是可以容忍。然而隨著振幅的變大，多尺度法的結果是令人無法接受的，當選擇A=0.2時，如圖3(c)，多尺度的誤差已經極大，而能量平衡法的位移結果尚佳。變分法和能量平衡法兩種方法得到的頻率結果精度雖然頗高,在對于模擬較大振幅的振動相圖時,會發現雖然位移誤差不大,但是速度誤差頗大, 如圖3(d)所示，因此本文提出一個基于能量平衡法的改進算法。

鑒于本文非線性項的階數最高為3階，可假設方程的解的形式為：

y=acosω10t+(A-a)cos 3ω10t

(43)

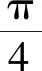
(44)

(45)

將H3、H4作差，令平均誤差為零：

(46)

如此可以解出未知系數a。

采用上述方法可解出當p=0.7，A=0.2和A=0.4時的系數a分別為：0.202 9和0.416 8，響應頻率ω10為4.966 2和5.021 6。如圖3(c)、(d)、(e)、(f)所示,在振幅很大，非線性很強時，本文的方法能獲得比能量平衡法更佳的近似逼近。尤其在圖3(e)、(f)可以看出, 本文方法的逼近數值解的精度尤高于能量平衡法。

(a) 振幅A=0.05時的時間歷程圖

(b) 振幅A=0.05時的相圖

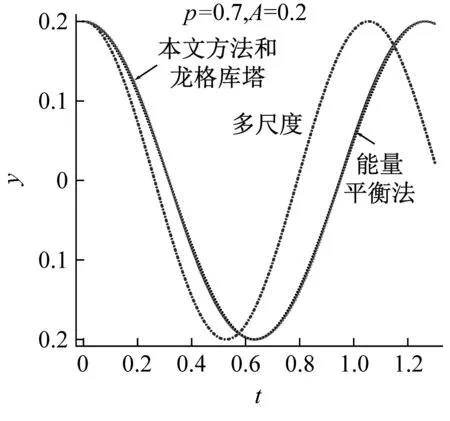
(c) 振幅A=0.2時的時間歷程圖

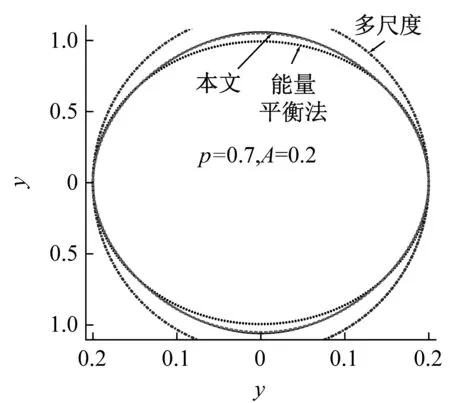
(d) 振幅A=0.2時的相圖

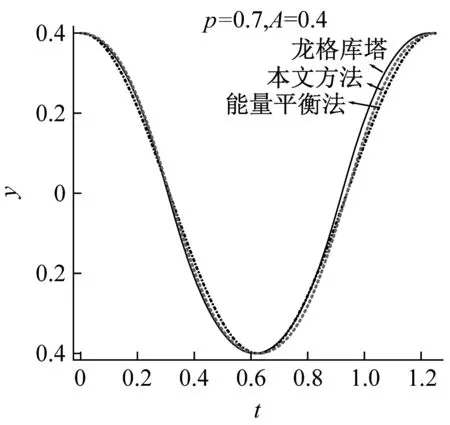
(e) 振幅A=0.4時的時間歷程圖

(f) 振幅A=0.4時的相圖

圖3p=0.7不同振幅下各方法的一階振型響應圖

Fig.3 Frequency-amplitude response for the first mode withp=0.7

經由以上的分析可知，響應頻率的表達式用(41)式應優于用多尺度法表示的(42)式，所以基于(41)式研究系統的漸硬或漸軟特性更為合理。當ω10大于原始基頻ω時，系統顯示漸硬特性；反之，為漸軟特性。

(47)

解得3α1>2ω2α2，因此用δ=3α1-2ω2α2大于零或小于零來判斷系統的漸硬、漸軟特性無論是對強非線性還是弱非線性都是合理的。對本文各例的有效非線性系數如表4所示。

表4 前兩階有效非線性系數δ

從表4可以看出,無論p的取值多少，一階振型均為漸硬特性；二階振型均為漸軟特性。

3 結 論

本文采用凱恩法的建模和基于超幾何函數和梅哲G函數對變截面梁的線性振型的表達是成功的。理論上得到了精確的線性振動基頻，不同于攝動法或半解析法，本法沒有取近似，所以結果準確和有限元法的對應結果良好。凱恩法得到的幾何非線性系數和慣性非線性系數和其他方法得到的系數也完全一致。

本文采用變分法和能量平衡法求解強非線性的幅頻響應是妥當的，在振幅較大時，即使多尺度法得到的結果已經完全失效時，這兩種方法的頻率結果仍非常可信。基于能量平衡法的改進法得到了更精確的響應近似表達式。

從變分法和能量平衡法得到的幅頻關系導出的有效非線性系數和用多尺度法導出的有效非線性系數具有完全相同的表達式。因此說明該表達式既適用于弱非線性也適用于強非線性振動。