考慮刀桿結構非線性的銑削過程顫振穩定性與主共振

2019-12-23 05:26:46任勇生馬伯樂馬靜敏

振動與沖擊 2019年23期

任勇生，馬伯樂，馬靜敏

(山東科技大學機械電子工程學院，青島 266590)

切削是機械零部件加工制造過程中的一個重要的環節。近年來，雖然先進制造技術已經取得了很大的進展，并且在航空航天和汽車等高技術領域的應用不斷增加，但是，切削過程中的顫振問題依然是嚴重影響機床切削效率的主要原因。

顫振是由于刀具與工件構成的閉環系統的動態不穩定引起的。顫振包括再生型和模態耦合型等。其中，再生型顫振是危害性最大的一種動態不穩定現象。顫振的發生會導致切削用量和加工質量降低，甚至會導致刀具損壞。因此，建立合理的顫振分析模型，準確揭示顫振發生的機理，對于實現有效的顫振控制，具有重要的意義。

現有的切削顫振建模與分析主要是在線性理論的框架內進行的。盡管早在1907年，Taylor[1]就已經發現了顫振現象，并將顫振看做生產率的極限，但對顫振現象的理論解釋卻是隨后五、六十年以后的事。Tobias等[2-5]基于線性理論，先后發現了顫振穩定性邊界，將過程參數空間(包括切削深度和主軸轉速)，劃分為穩定和不穩定區域。Tobias在切削力中引入時滯失穩項，提出了再生理論，該理論被認為是迄今為止能夠對顫振現象給出完整解釋的理論。Altintas及其合作者們基于再生效應和實驗模態分析提出了車、銑和鉆加工過程的顫振預測理論[6-8]。為了準確確定經典顫振穩定性數學模型所涉及到的參數，遲玉倫等[9]提出了基于實驗設計并利用遺傳算法的參數預測方法。理論計算顫振的穩定性lobes圖結果與實驗測量結果相一致。

由于線性理論不能預測切削過程的某些重要的現象，因此，近年來有關切削系統的非線性建模開始引起人們關注。切削系統非線性的主要來源涉及結構非線性、平方和立方非線性項時滯切削力以及和冪函數切削力等等[10-13]。Hanna等首次提出一個具有平方和立方結構剛度和切削力的時滯非線性模型。該研究激發了人們對分析此類問題的全局動力學的極大的興趣。切削系統非線性理論的有效數學方法包括：中心流理論、分叉理論、攝動分析、相軌線和Poincaré截面等。毛漢穎等[14]針對切削顫振具有非線性特征，常規信號處理方法無法全面揭示顫振特征的問題，基于關聯維數、最大Lyapunov 指數和Kolmogorov 熵，研究測試信號的混沌特征以及切削過程從平穩到顫振的變化規律。吳石等[15]采用工件振動信號的最大Lyapunov指數作為閾值，通過實驗判定航空鋁合金7075-T6兩端固定薄板件銑削加工過程的顫振穩定性。

Pratt[16]采用多尺度法、諧波平衡法和Floquet理論，研究Hanna和Tobias的模型，結果表明，由于三次結構非線性的存在，可能產生亞臨界Hopf分叉。Moradi等[17]研究考慮刀具磨損和過程阻尼的切削過程的不同分叉類型的存在性，他們使用二自由度線性模型對刀具進行結構建模，切削力則采用多項式非線性模型，采用多尺度法構造出主共振近似分析解。Moradi等[18]采用與文獻[17]類似的模型分析銑削過程的受迫振動，他們不僅研究主共振同時也討論了超諧共振以及內共振的情形。Moradi等[19]同時考慮切削力和結構非線性，研究了銑削過程的內共振和再生顫振。Jalili等[20]考慮陀螺矩和轉動慣量，建立三維非線性刀具結構模型，采用多尺度法研究銑削系統的主、亞和超諧共振。Jung等[21]將刀具簡化為二自由度模型，對具有切削力非線性和再生特性的銑削過程進行分叉分析。采用多尺度法和諧波平衡法研究系統的局部顫振特性。

從上面的分析可以看出，切削過程的再生顫振是高度非線性的。盡管人們已經考慮包括切削力和刀具結構在內多種非線性因素的影響，而且，所提出的復雜非線性模型能夠對物理現象給以較好的解釋和描述，但絕大多數的研究還僅僅是建立在簡單的二自由度非線性模型基礎上的。缺少切削系統中刀桿模型的建立與分析過程。此外，切削系統結構阻尼的建模與影響也沒有予以考慮。

本文研究銑削系統的非線性顫振與主共振。將刀桿簡化為具有平面彎曲的懸臂梁。非線性來源于刀桿的不可伸長假定，刀桿的材料假定為黏彈性材料，采用Kelvin-Voigt方程對此進行描述。基于Hamilton原理導出切削系統的非線性顫振運動方程。為了得到振動方程的封閉解，首先采用Galerkin法對運動偏微分方程進行離散化，得到廣義坐標表示的非線性常微分運動方程。采用多尺度法對切削系統在周期變化切削力作用下的穩態受迫響應，進行近似求解。通過數值計算研究了刀桿的幾何尺寸(包括長度和直徑)、阻尼、切削系數、切削深度、齒數和切削力幅值等參數，對銑削過程非線性lobes圖以及主共振響應曲線的影響。

1 數學模型與求解

刀桿的動能

(1)

式中：m為刀桿質量，L為刀桿長度，u和v表示橫截面任意點沿x和y方向的位移，即縱向位移和橫向位移。“·”表示對時間t求導數。

假定不考慮剪切應變，則橫截面上任意點的應變為

εx=e-yρ

(2)

式中：y表示橫截面上點的位置坐標，ρ表示曲率，e表示沿刀桿中心線的應變，表示為

(3)

式中：u表示橫截面沿x方向的位移，“’”表示對x求偏導數。

刀桿應變能的變分為

(4)

式中：σx為應力分量。

假定刀桿為黏彈性材料所構成，其應力應變關系滿足Kelvin-Voigt方程如下

(5)

式中：E是彈性模量，C是阻尼系數。

假定刀桿為不可伸長的，即e=0，由此可得

(6)

于是，曲率ρ可近似為

(7)

利用關系式(6)解出u并且對時間求導數，并且將結果代入方程(1)，得

(8)

根據動能和應變能表達式，利用Hamilton原理，可導出運動方程如下

(9)

式中:上標“(4)”表示對x求四階偏導數。f(x,t)=ΔF(t)δ(x-L)，δ為狄拉克函數。ΔF(t)表示作用在刀桿端x=L的切削力，表示如下

ΔF(t)=Ktwh(t)=

Ktw[h0-(v(L,t)-v(L,t-τ)]+FcosΩt

(10)

式中：Kt表示切削系數，w表示切削深度，h(t)表示動態切削厚度，τ表示刀齒轉動周期，τ=2π/NΩ，N是刀齒數，Ω為轉速。F表示切削力中周期成分的幅值。在切削力表達式(10)中，一般不考慮靜態切削厚度h0的影響[18,22]。在后面的分析中，令h0=0。

為了尋求非線性運動方程(9)的近似解，首先采用Galerkin法進行化簡，令

(11)

代入式(9)，由Galerkin法，得

(12)

其中

V=V(t),

Vτ=V(t-τ)

(13)

令

(14)

按照單自由度系統線性振動理論，可導出下列關系式

(15)

式中：ω1和η分別表示刀桿的第一階固有頻率和損耗因子。

方程(12)可以寫成

(16)

研究切削系統的非線性顫振穩定性，則需要在式(16)中令周期激勵項等于0，并對此方程進行數值積分，可得到穩定性lobes圖。

多尺度法是非線性振動分析的一種有效的方法，它不僅能計算穩態響應，而且能計算耗散系統的衰減振動。但多尺度法不適合于求解強非線性系統，只適合于小參數弱非線性系統。

為了獲得系統的主共振響應近似解，下面我們將采用多尺度法對方程式(16)進行攝動分析。為此引入小參數ε，將式(16)寫成

(17)

同時，引入調諧因子σ表示固有頻率ω1與轉速的接近程度

Ω=ω1+εσ

(18)

按照文獻[18]，通過拉氏變換并利用Pade近似e-sτ≈1-sτ，對方程(17)中的時滯項V-Vτ進行簡化之后，方程(17)化為

(19)

將方程(19)的解按小參數ε展開

V=V0(T0,T1)+εV1(T0,T1)+…

(20)

式中：T0=t、T1=εt分別為慢變、快變時間尺度。

利用下列時間導數鏈式規則

(21)

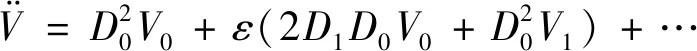
(22)

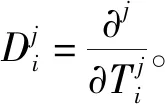
ε0:

(23)

ε1:

(24)

方程(23)的解為

(25)

將式(25)代入式(23)，消除永年項，得

(26)

令

(27)

式中：a和ψ為T1的函數，分別表示振幅和相位角。

令σT1-ψ=Γ，則方程(26)可寫成

(28)

分離實部與虛部，得

(29)

其中

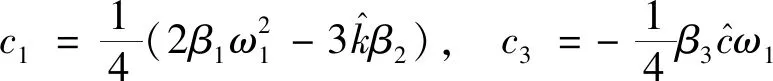
(30)

為了求穩態響應，令a′=Γ′=0，并且消去Γ，得

σ=

(31)

2 數值結果與討論

2.1 穩定性lobes圖

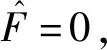
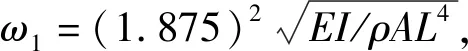
圖1表示刀桿長度對切削穩定性邊界的影響。結果表明，穩定性lobes圖在切削深度-轉速參數平面的位置隨著刀桿長度L的增加而下降，同時穩定性邊界的轉速區間也隨著刀桿長度L的增加而縮小。這說明增加刀桿的長度將對切削穩定性將產生不利的影響。

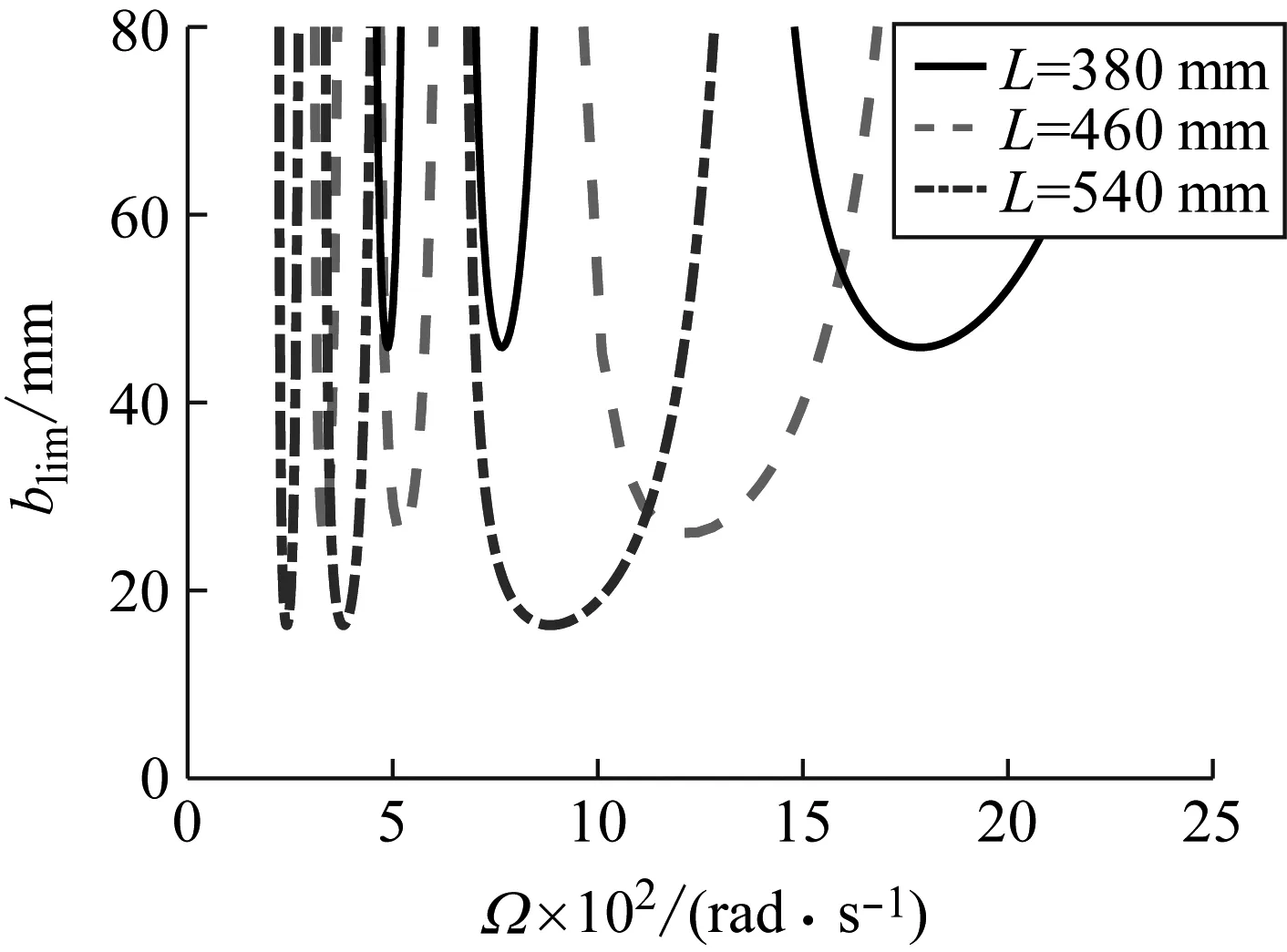
圖1 刀桿長度對穩定性lobes曲線的影響

圖2表示刀桿直徑對對切削穩定性邊界的影響。結果表明，切削系統的穩定性隨著刀桿直徑的減小而隨之降低。這是由于在刀桿長度不變的情況下，刀桿直徑的減小伴隨著刀桿長徑比的增加。說明大長徑比的刀桿的穩定性相對較差。

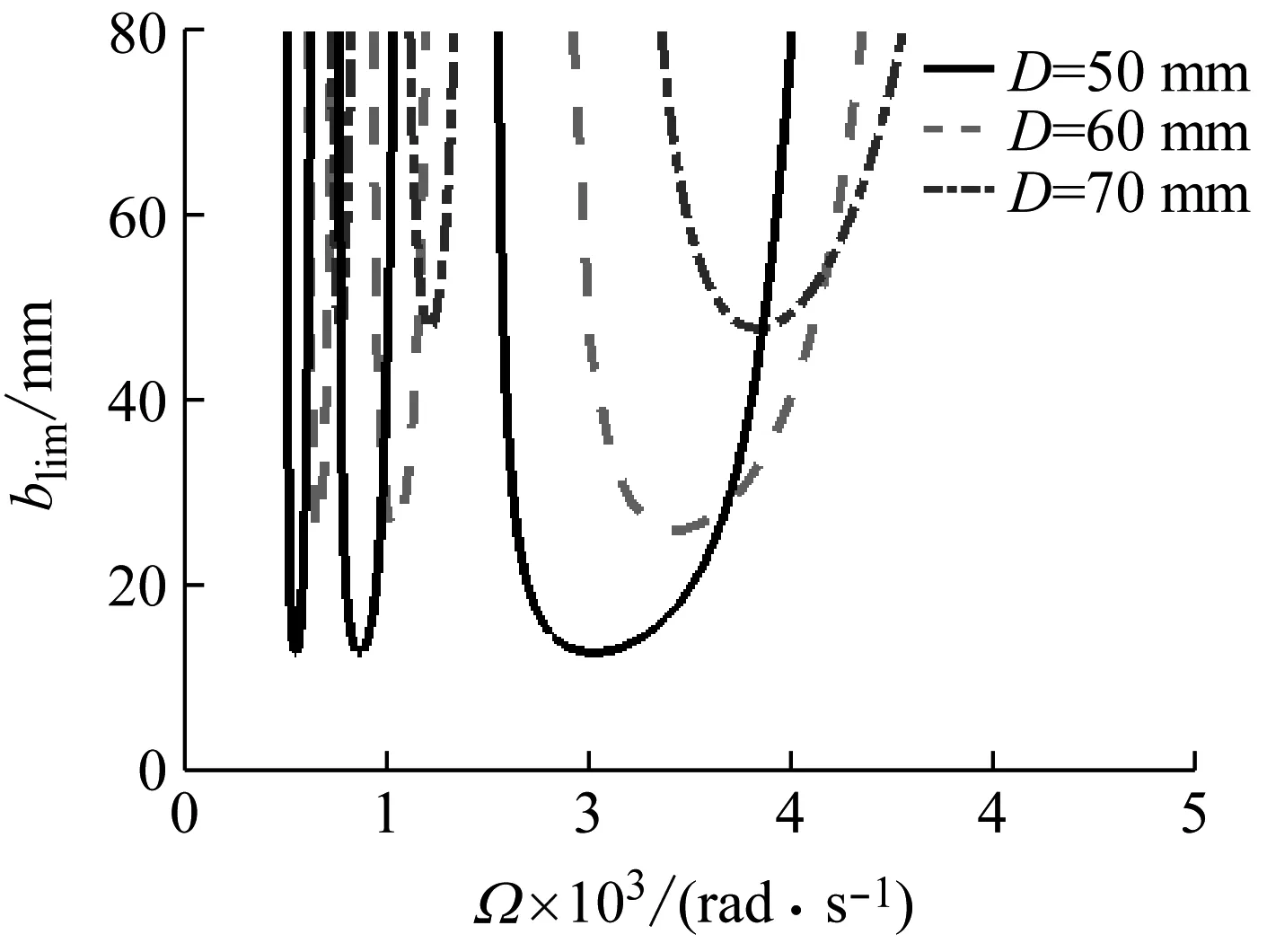
圖2 刀桿直徑對穩定性lobes曲線的影響

圖3表示刀桿材料的耗散因子對切削穩定性邊界的影響。結果表明，提高刀桿的阻尼耗散能力對于抑制切削顫振，增強加工過程的穩定性具有十分重要的影響效果。

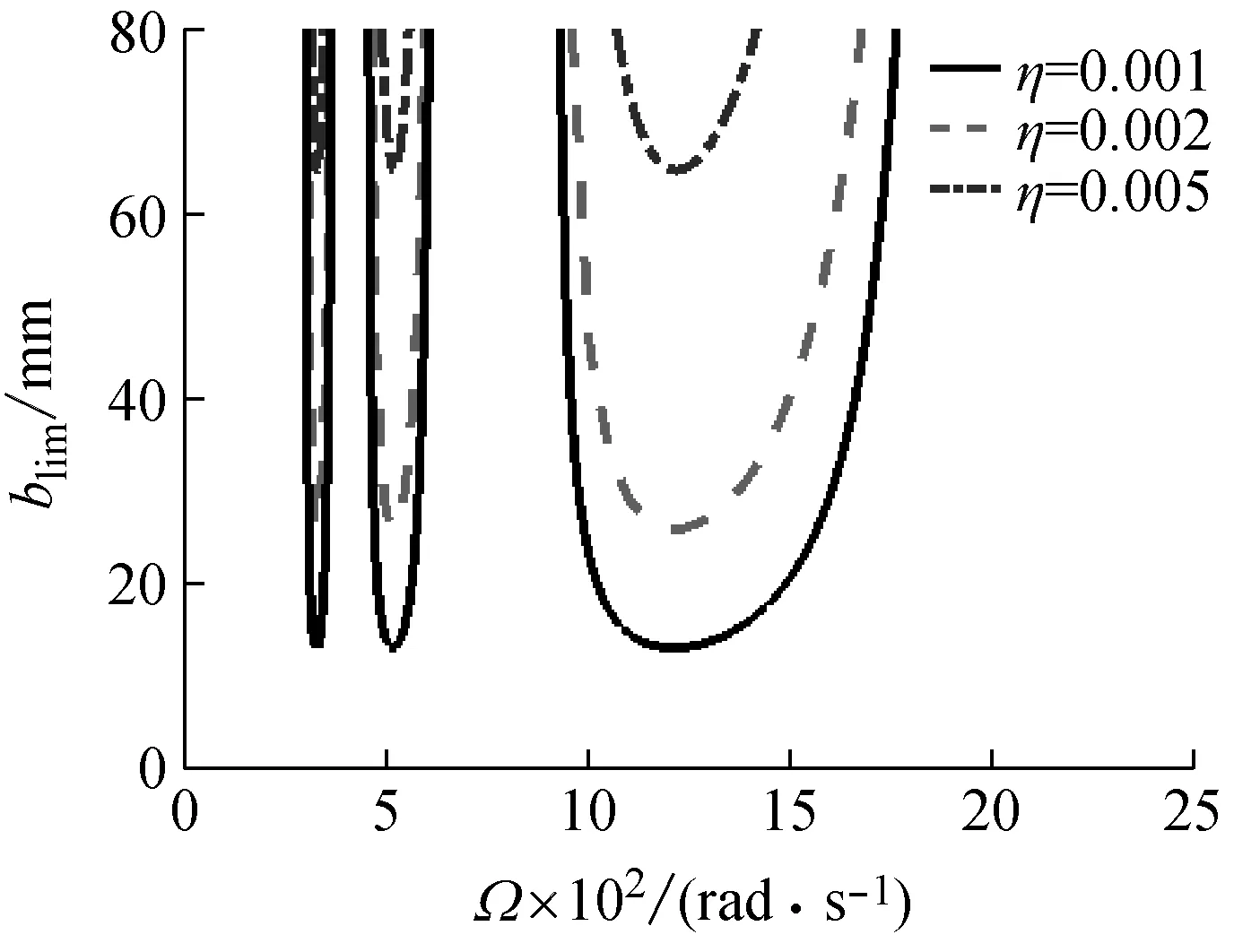
圖3 結構阻尼對穩定性lobes曲線的影響

圖4表示切削力系數對切削穩定性邊界的影響。結果表明，Kt越大，切削過程越不穩定，越容易發生顫振。

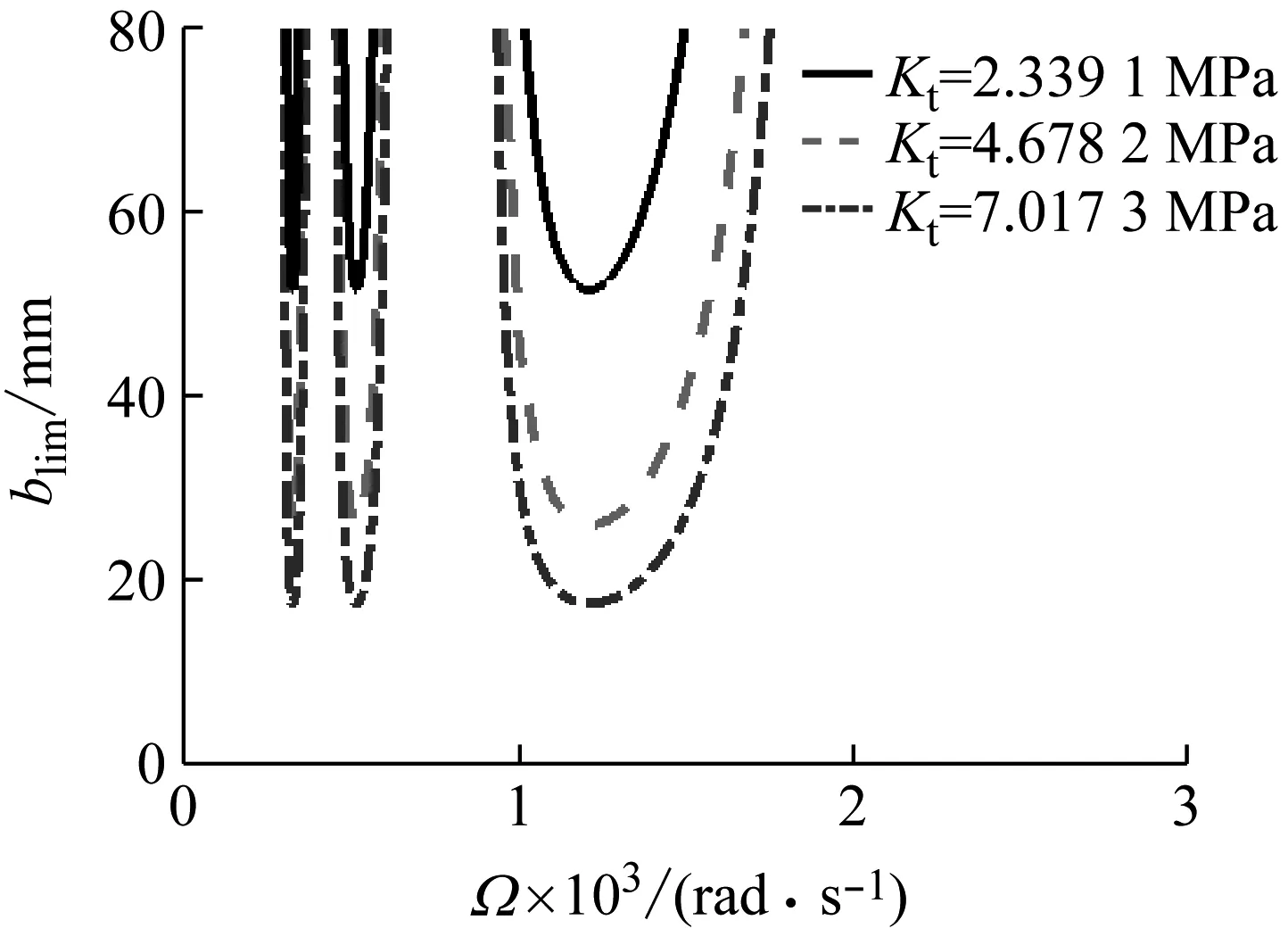
圖4 切削力系數對穩定性lobes曲線的影響

圖5表示分布在穩定性參數平面的12個點的位置，與之對應的切削深度與轉速值如表1所示。圖6表示這12個位置點的時程響應曲線v(L,t)。由圖5和6可見，點1、3、5位于lobe曲線的不穩定區域內，對應的時程的振幅是隨時間增大的，但是由于非線性剛度的抑制作用，響應振幅不會無限增大，而是被限制在一定的范圍之內，這與線性系統理論的結論是不同的；點7、8、9位于lobe曲線的邊界上，時程響應振幅保持不變，對應的切削過程是臨界穩定的；點2、4、6、10～12位于穩定區域之內，對應的時程響應曲線是隨時間減小的。

圖5 位于穩定性lobes曲線所在平面的參數點位置

Fig.5 The position of parameters points located at the plane of the stability lobes

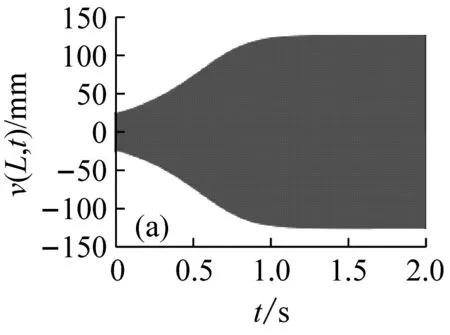
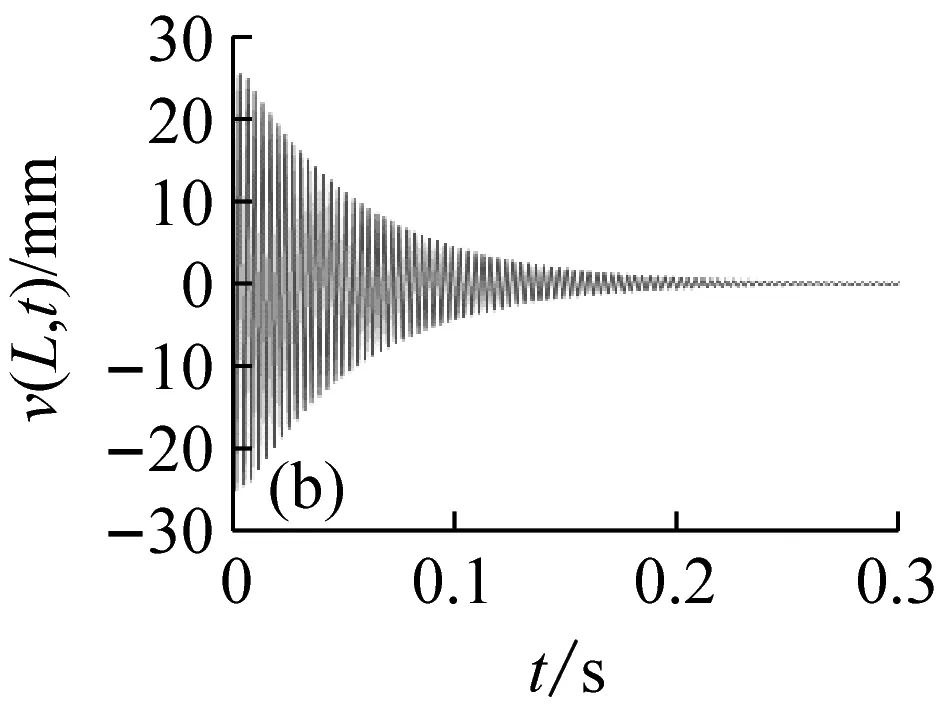
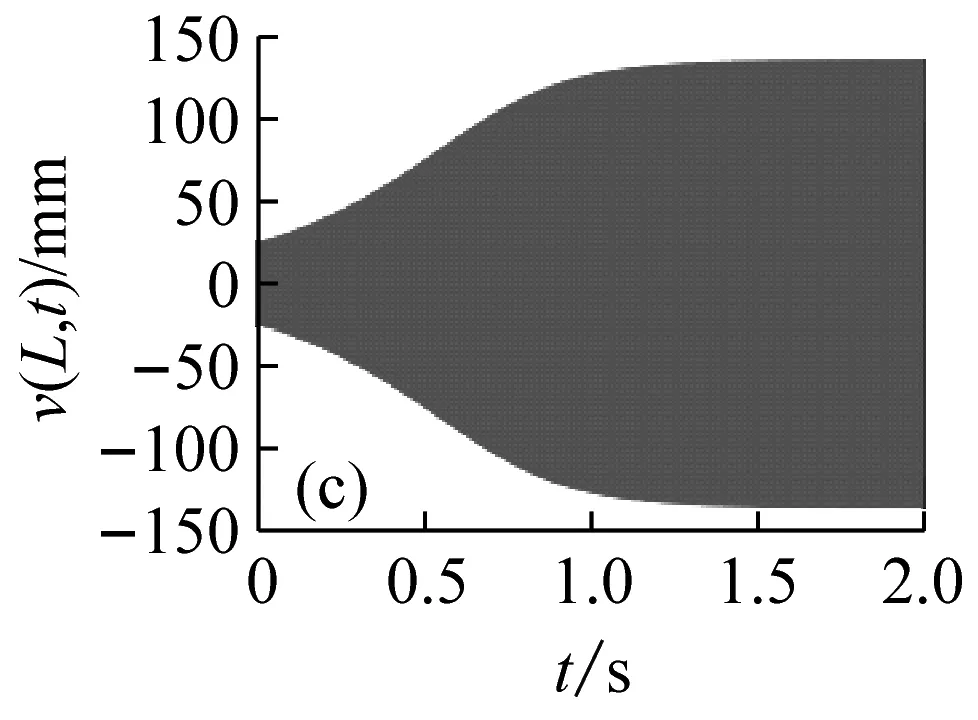
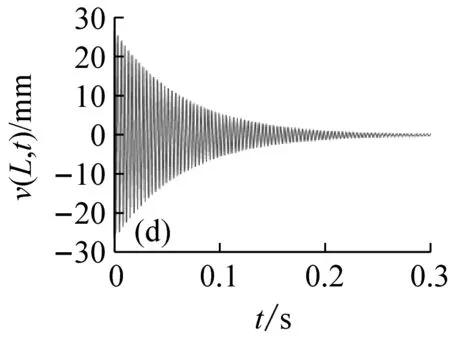
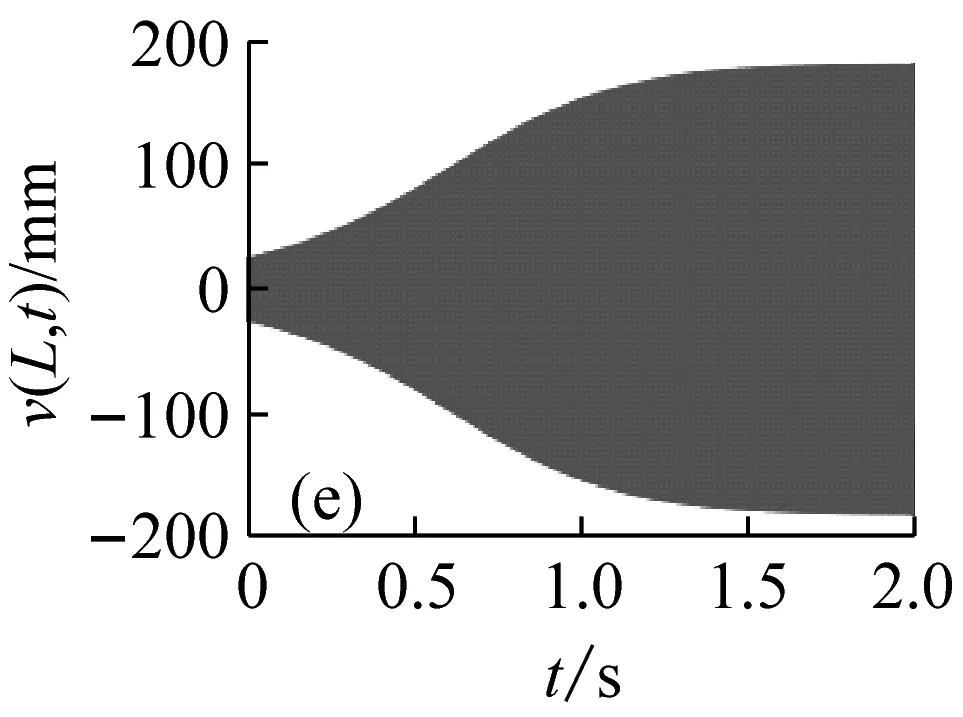
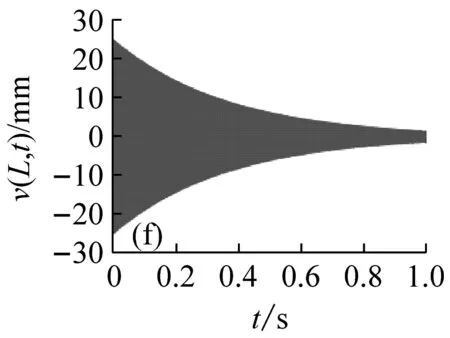
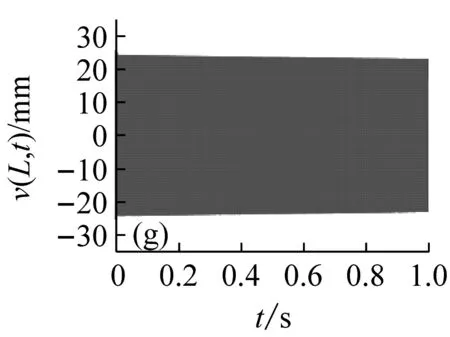
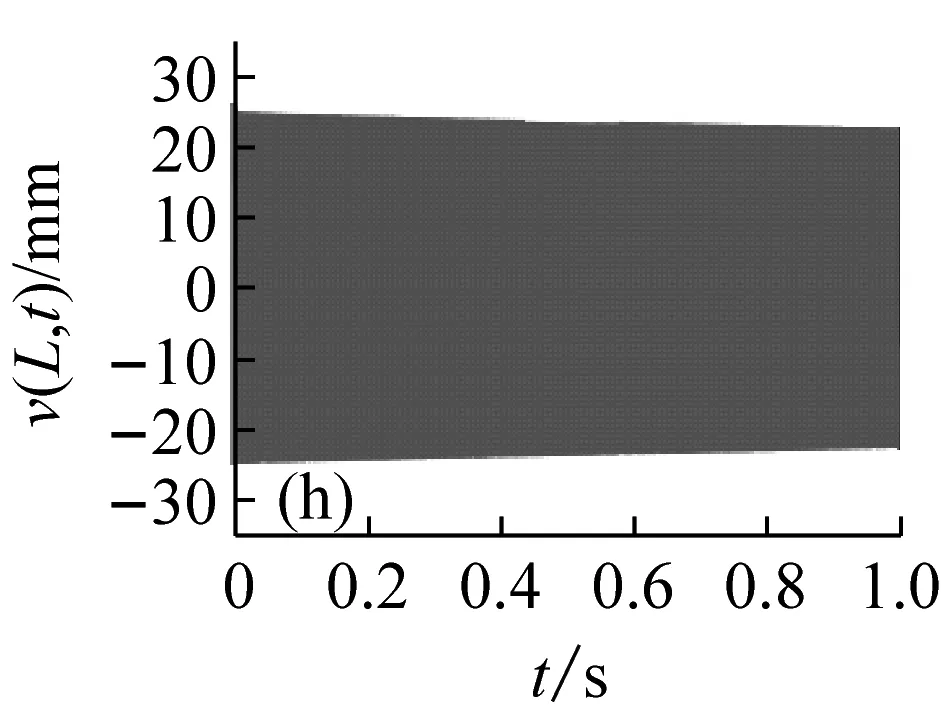
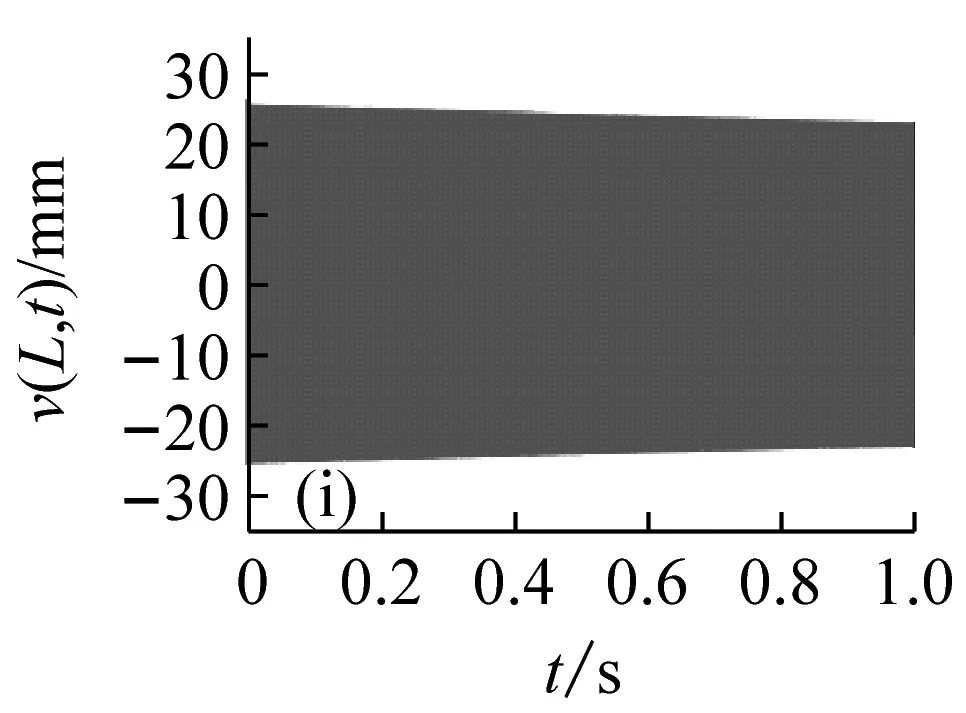
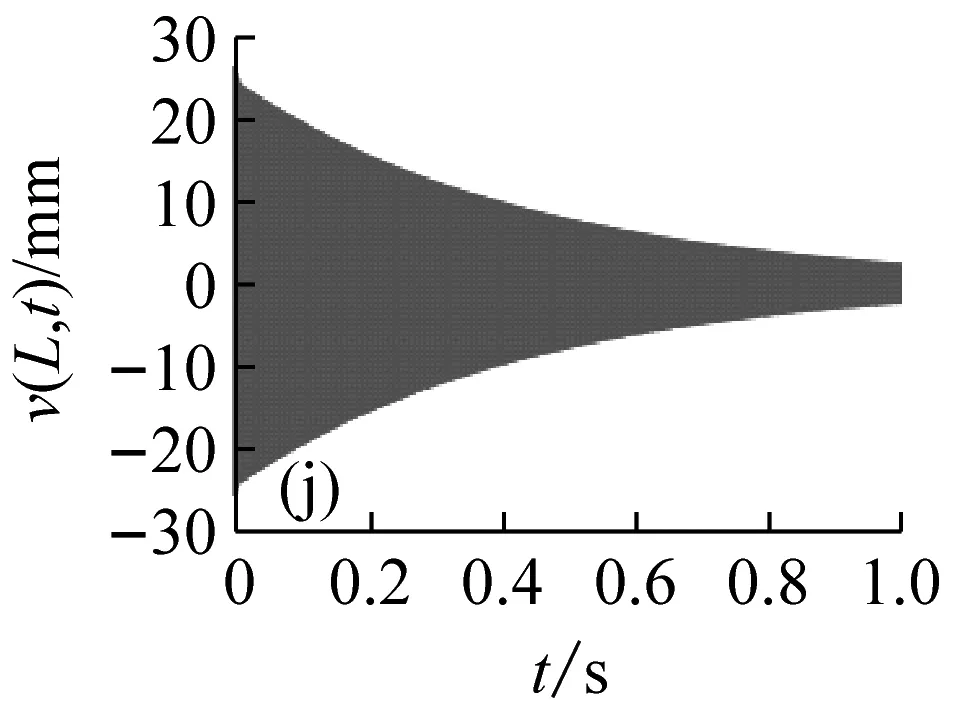
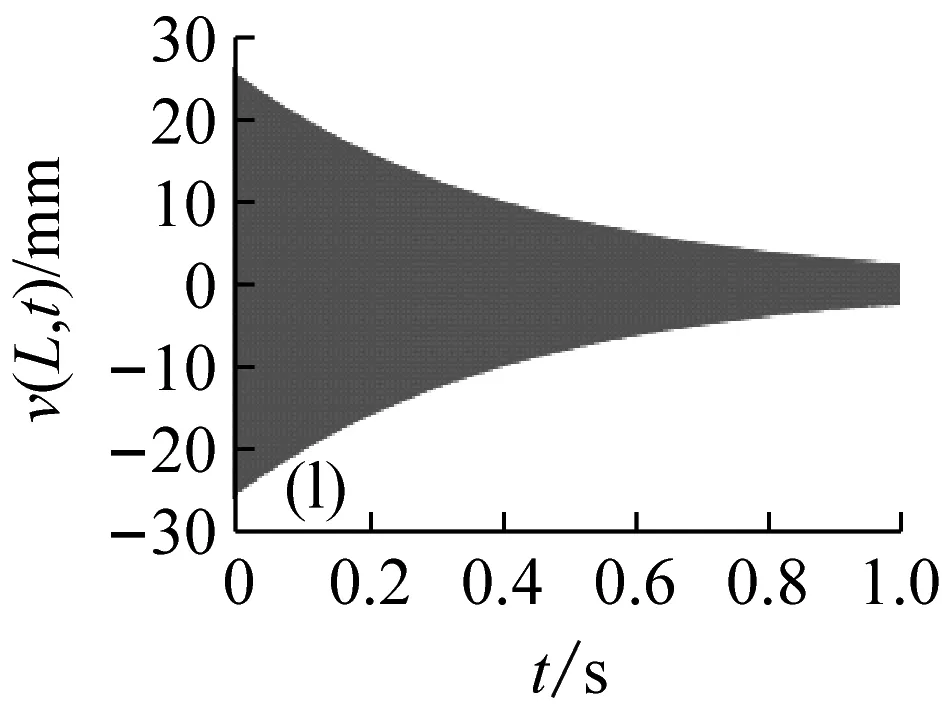
圖6 與圖5參數點對應的時程響應曲線

Fig.6 The time history response curves that correspond to the parameters points in Fig.5

2.2 主共振響應

為了研究切削系統的非線性受迫響應特性，我們從方程式(31)出發，給定調諧因子σ，計算對應的受迫響應幅值a。畫出a隨σ變化曲線，即主共振響應曲線。研究切削系統的參數對主共振響應曲線的影響。

圖7表示L對主共振響應特性的影響。結果表明，主共振響應曲線峰值向右偏斜，表現典型的硬彈簧Duffing振子的特性。主共振響應出現跳躍性和多值區域。這主要是切削系統存在三次剛度非線性所決定的。由圖7可見，刀桿越短，振幅越小，非線性響應特征也越明顯。結構非線性的存在對振動響應有限制作用。

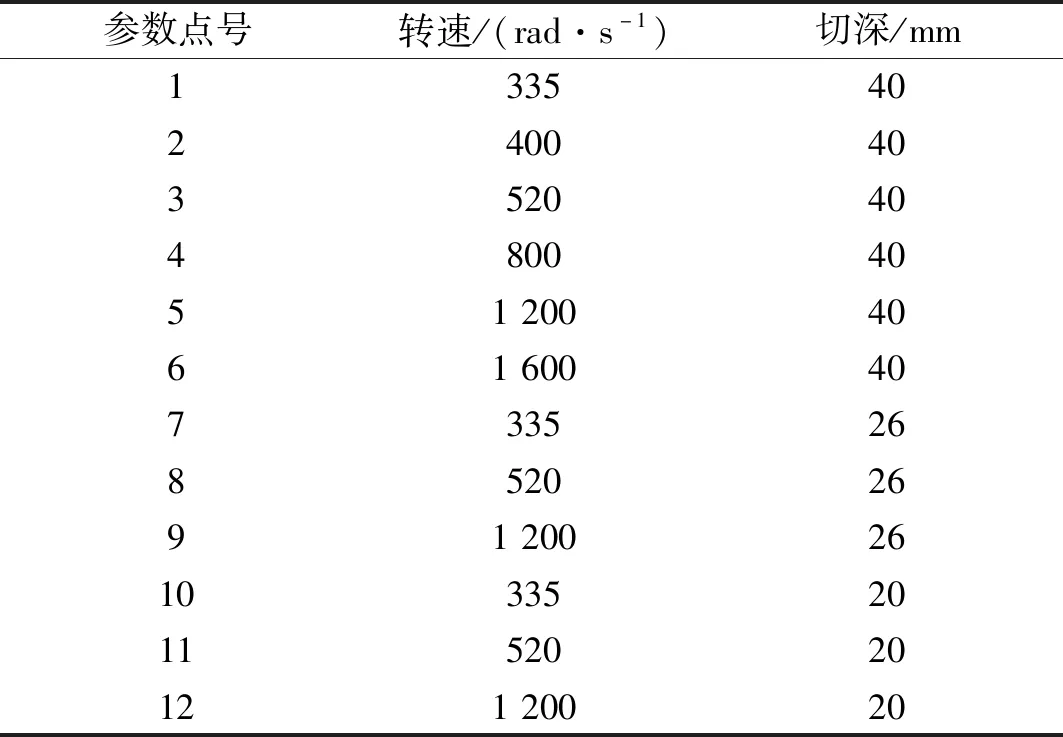
表1 圖5中各點對應的參數值

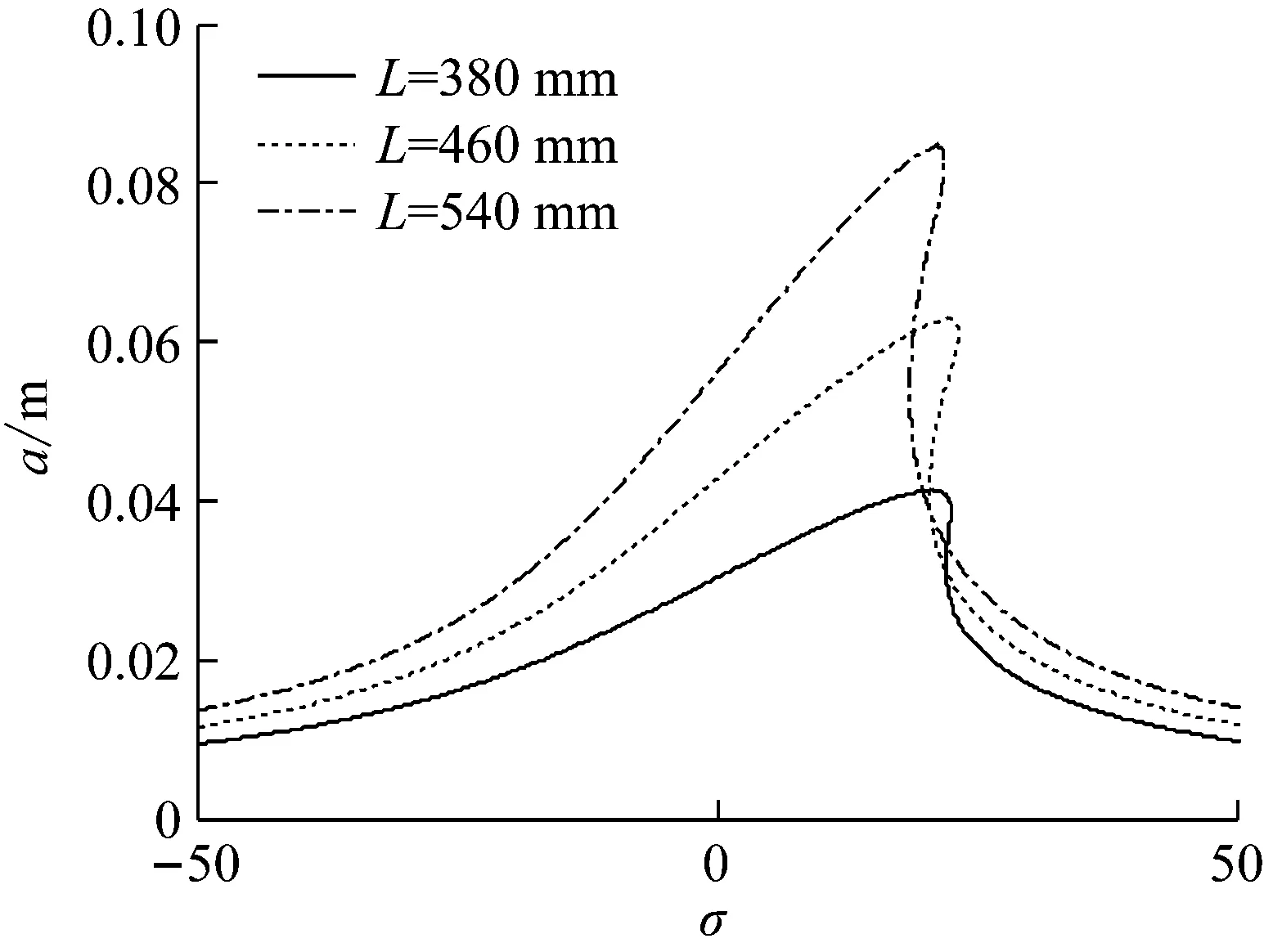
圖7 刀桿長度對主共振曲線的影響

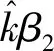
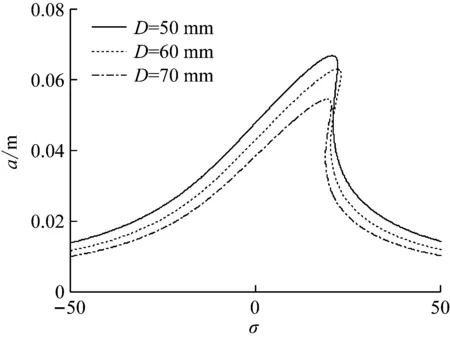
圖8 刀桿直徑對主共振曲線的影響

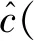
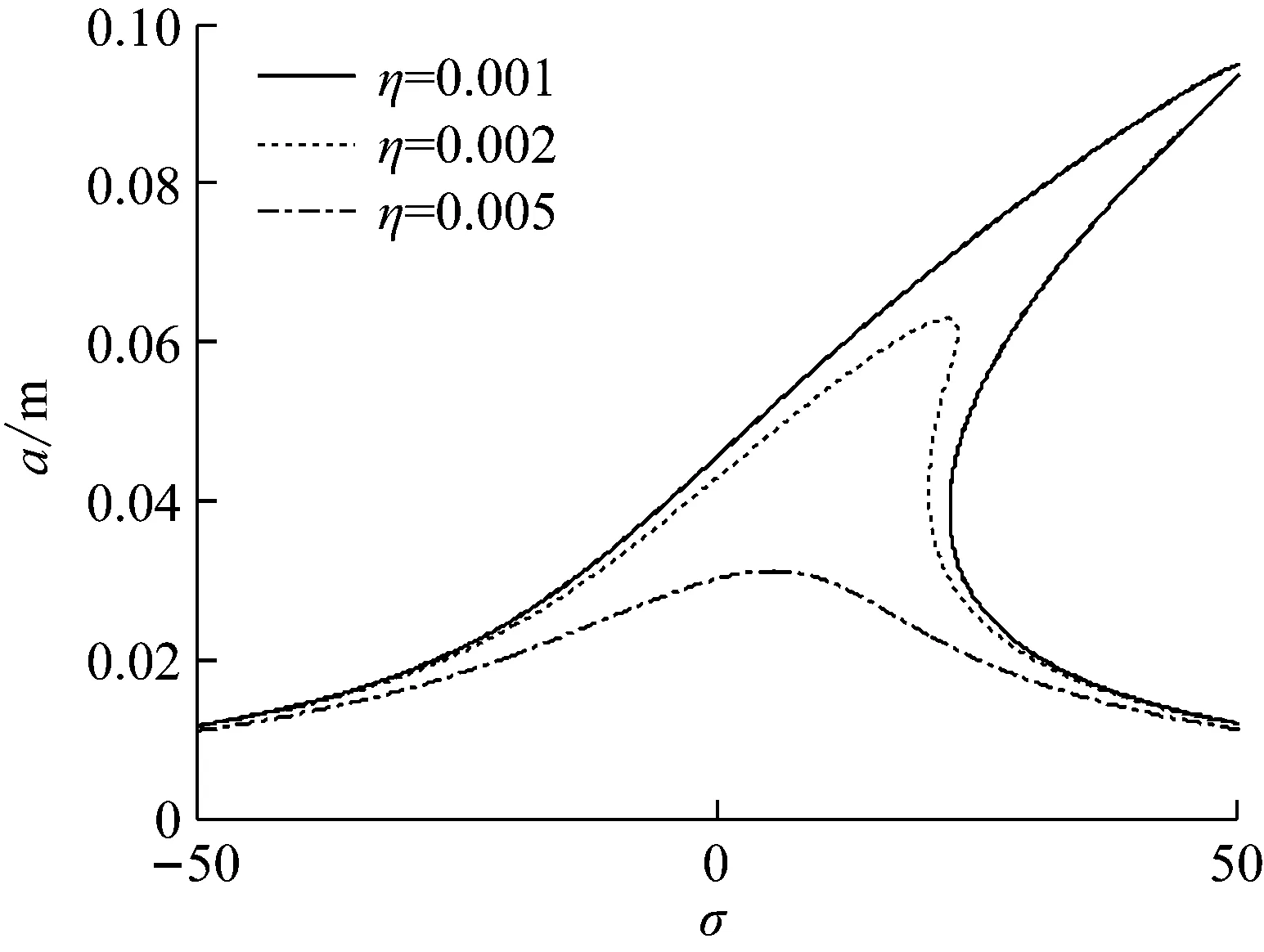
圖9 結構阻尼對主共振曲線的影響

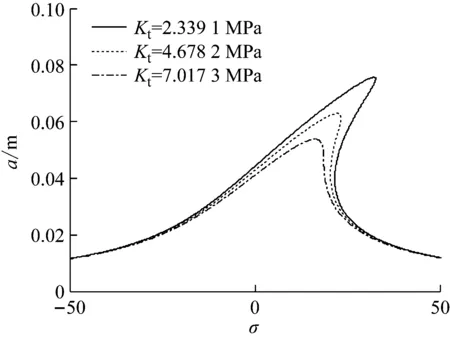
圖10 切削力系數對主共振曲線的影響

圖11表示切削深度Wc對主共振響應曲線的影響。結果表明，增加切削深度會導致主共振響應幅值的降低。對上述結果的物理解釋與對圖10的解釋相同。

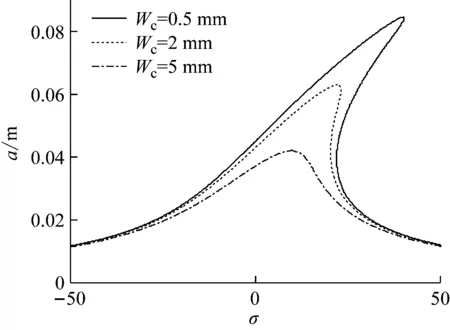
圖11 切削深度對主共振曲線的影響

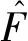
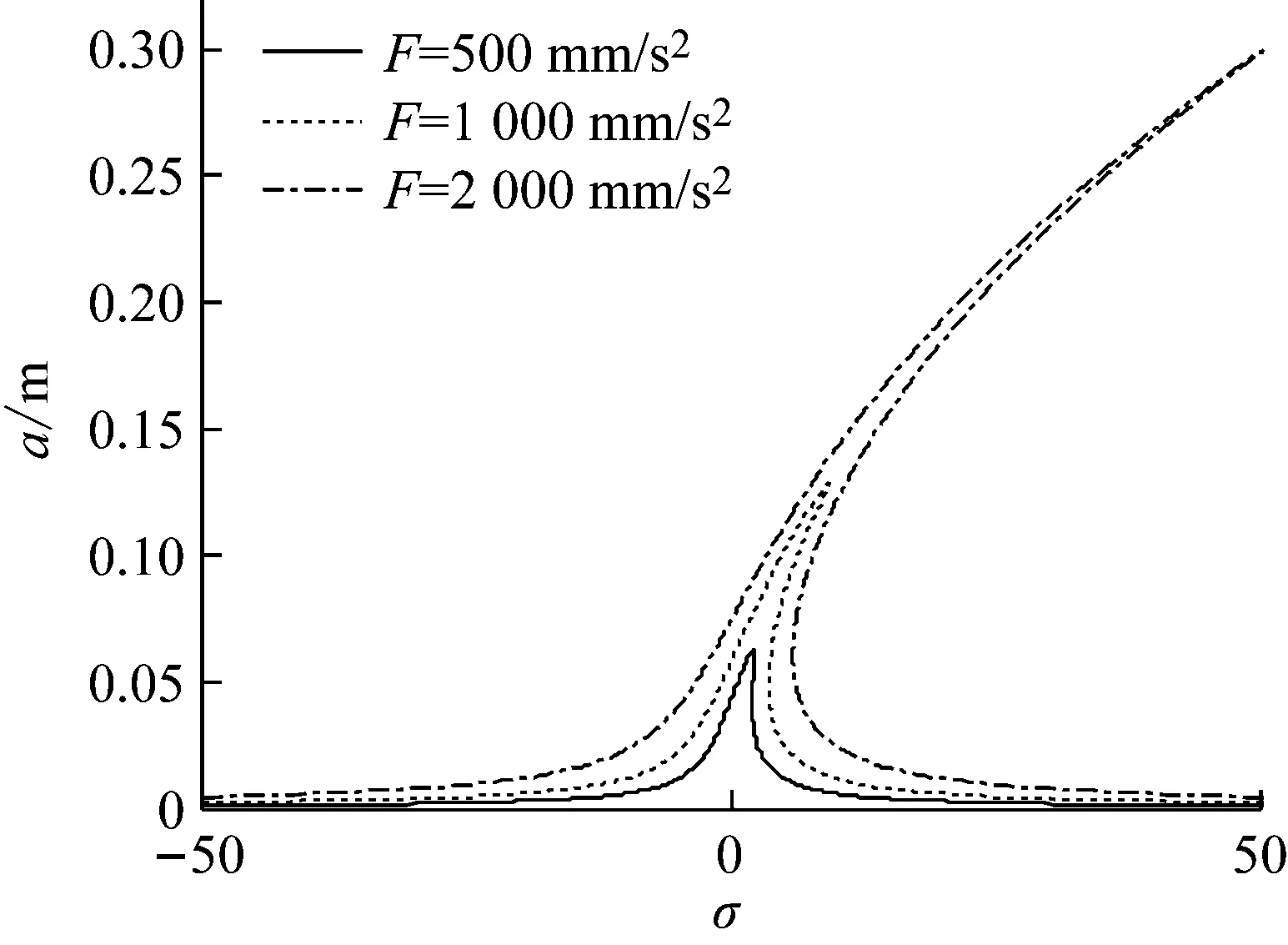
圖12 周期激振力幅值對主共振曲線的影響

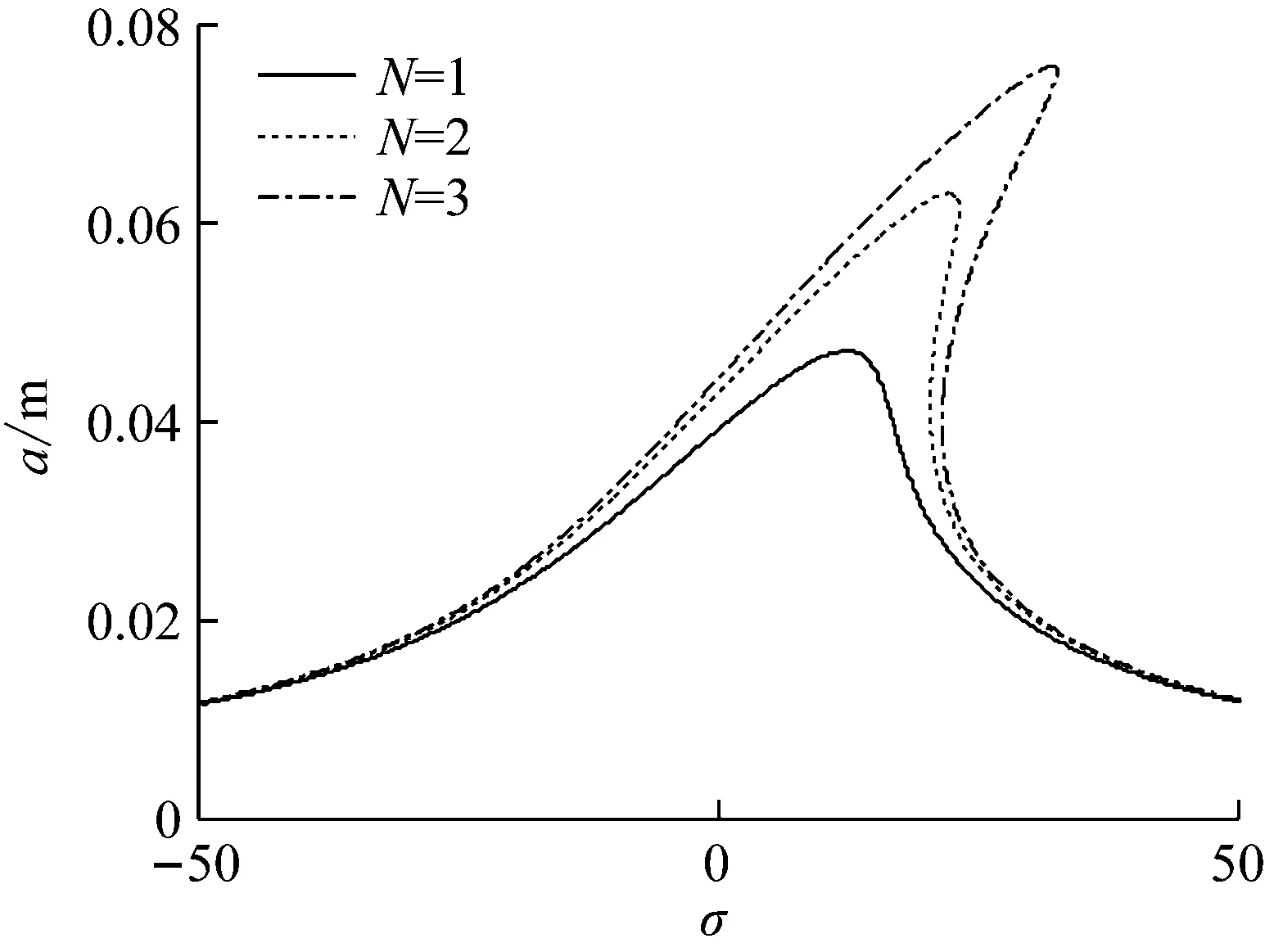
圖13 刀齒數對主共振曲線的影響

圖14表示三次非線性慣性項對主共振響應的影響(L=460 mm，D=60 mm，η=0.002，Kc=4.678 2 MPa，Wc=2 mm，N=2，F=2 000 mm/s2)。由圖14可以看出，三次非線性慣性項雖然不改變主共振峰值響應的大小，但對主共振響應曲線的彎曲程度有明顯的限制作用，存在三次非線性慣性項的主共振響應曲線的非線性程度與不考慮考三次非線性慣性項的情形相比，似乎相對較低。

圖14 非線性慣性項對主共振曲線的影響

Fig.14 The effect of number of nonlinear inertial term on primary resonance curves

圖15表示阻尼相關非線性項(表示為位移平方與速度一次方的乘積)對主共振響應的影響，計算參數與圖14取值相同。由圖15可以看出，阻尼相關非線性項不改變主共振響應曲線的形狀，但存在阻尼相關非線性項的系統的主共振響應峰值相對更大，這和與速度一次方成正比的線性阻尼對主共振響應峰值的作用，剛好相反。

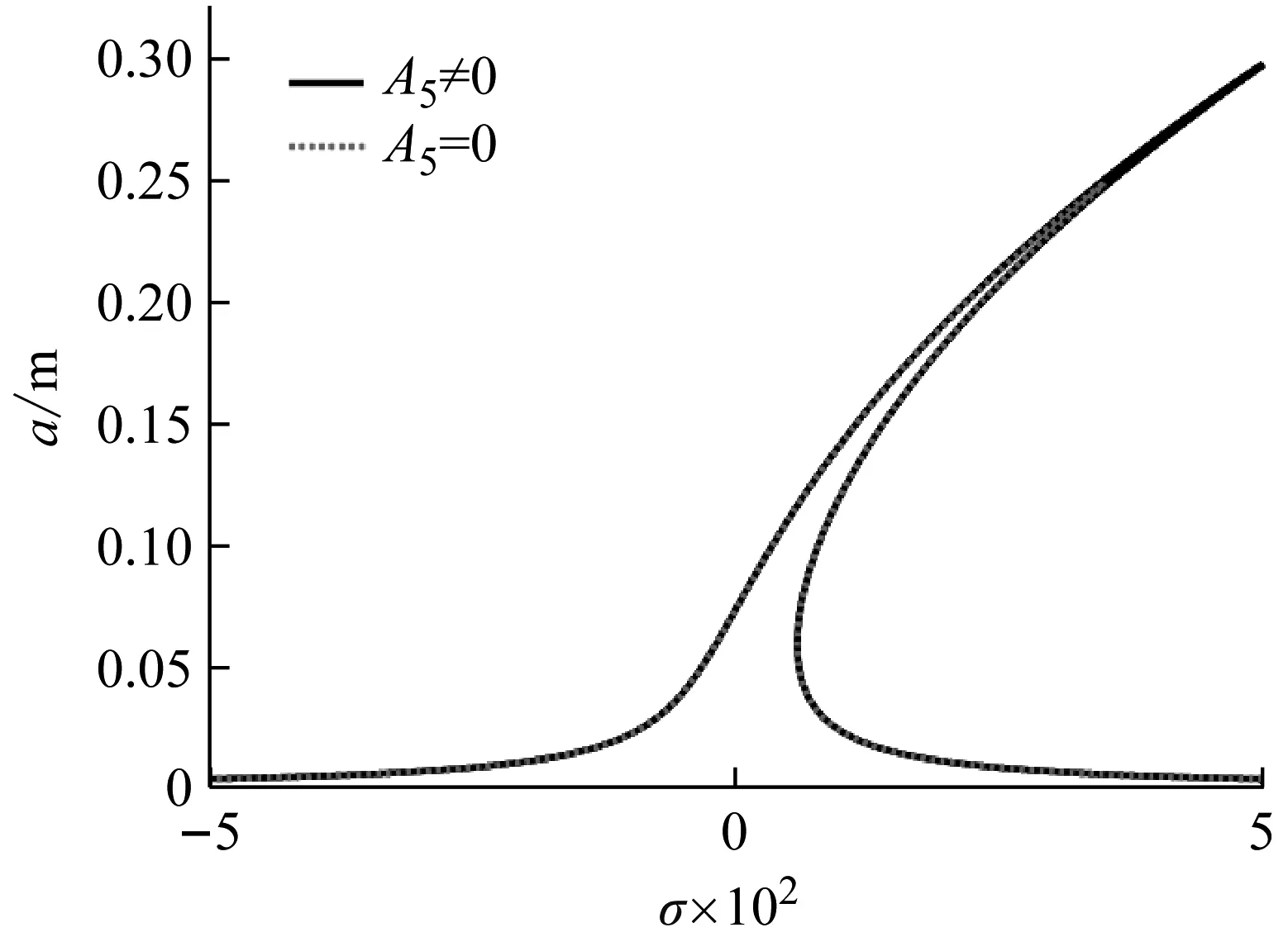
圖15 非線性阻尼項對主共振曲線的影響

Fig.15 The effect of number of nonlinear damping term on primary resonance curves

最后，將本文模型得到的穩定性lobes圖與文獻[23]進行了對比(見圖16)，圓形截面刀桿的計算參數均取自文獻[23]：長度為460 mm，直徑D=60 mm，密度為7.85 g/cm-3，彈性模量為210 GPa，泊松比為0.3，阻尼比為0.05，切削剛度Kc=2 339.1×106N/mm2。結果表明，如果在本文模型中不考慮幾何非線性的影響，所得到的線性lobes圖與文獻[20]的計算結果是一致的。此外，對比結果也表明，由非線性lobes圖得到的最小切削深度大于線性系統的最小切削深度，導致這個結果的原因是考慮結構非線性的刀桿的彎曲剛度較之線性刀桿會有所增加，于是，非線性切削系統的剛度也會隨之增加，從而導致非線性切削穩定性的提高。

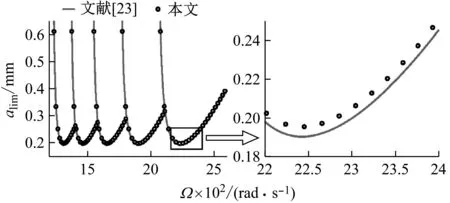
圖16 非線性與線性穩定性lobes圖

3 結論

研究考慮刀桿結構非線性以及材料阻尼的銑削系統非線性顫振與主共振。將刀桿結構簡化為平面彎曲懸臂梁，并假定刀桿由黏彈性材料構成。基于Hamilton原理并結合含有周期激勵的再生型切削力模型，建立銑削系統非線性顫振運動模型。采用Galerkin法對運動方程進行簡化，采用多尺度法導出切削系統的主共振響應近似解。通過數值計算得到非線性切削系統的lobes圖和主共振曲線。研究了刀桿的幾何尺寸、結構阻尼、切削力系數、切削深度、齒數和切削力幅值等參數對顫振穩定性和主共振響應特性的影響。結果表明：

(1) 增加銑刀齒數、激振力幅值或者減小切削力參數、切削深度，能夠增加主共振響應曲線的峰值；結構阻尼對主共振響應有明顯的抑制作用。

(2) 由于切削系統存在三次剛度非線性，主共振響應峰值向右偏斜，切削系統的主共振響應表現出典型的硬彈簧Duffing振子的特性，出現跳躍性并且存在多值區域。

(3) 結構阻尼對切削系統的顫振穩定性產生顯著的影響，結構阻尼越大，切削穩定性越好。

(4) 減小刀桿的長徑比(如減小長度或增加直徑)，或者減小系統切削力參數，均能夠增加銑削顫振的穩定性區域。