采用時延狀態觀測器的旋翼無人機自適應編隊控制

徐振,李勝,陳慶偉,季蔡娟

(南京理工大學自動化學院,210094,南京)

近年來,旋翼無人機以其成本低、操作簡單的特點和優異的中低空機動性能,受到了使用者的青睞。如今在物資運輸、森林滅火、目標追蹤、戰場偵察與打擊、電力巡線等場景,無人機發揮著越來越重要的作用。目前,無人機之間的通信延遲和變質量慣量等行為,制約著無人機編隊的精度及其執行任務的能力,而無人機的編隊是提高無人機工作效率的有效方式。

常見的編隊方法有領航跟隨法、虛擬結構法、基于行為法、一致性算法等。基于行為法實現簡單,多適用于未知環境,但編隊收斂性很難進行精確的數學證明;虛擬結構法和領航跟隨法類似,要求核心無人機的全狀態反饋信息,原理簡單,便于工程實現,但對核心無人機的安全性和魯棒性要求較高,當智能體增多時,運算量較大[1];一致性算法最早由Ren[2]和Liu等[3]引入到多智能體系統的編隊控制中,其分布式的特點具有良好的魯棒性,在智能體較多的情況下優勢明顯。文獻[4]中用一致性理論進行多機器人的隊形控制和穩定性分析;文獻[5]對高階線性模型的一致性協議運用中的時變隊形和時延問題進行了討論。本文考慮小型無人機編隊,結合全文側重點和文獻[15],采用領航跟隨法進行編隊飛行。

一方面,針對無人機編隊在復雜環境中的通信延遲問題,學者們已提出多種處理方法,例如:文獻[6]針對一類二階異質多智能體系統的時延問題,提出了一種無假設條件的異質多智能體系統靜態組一致性算法;文獻[7]通過變量代換,將時延條件下的線性群系統編隊控制問題轉化為時延系統的鎮定問題,以構造李雅普諾夫函數;文獻[8]針對一類無速度傳感器的靈巧型噴氣式無人機設計時延觀測器,用于估算自身狀態。現階段的文獻中,時變時延多采用被動的處理方式,即通過一致性協議設計,在得知通信延遲變化率等先驗條件的前提下,實現無人機群系統跟蹤誤差有界,但通常誤差無法收斂到0,或具有一定的保守性,收斂速度較慢,而將時延狀態觀測器用于旋翼無人機編隊的可參考案例也相對較少。

另一方面,無人機擔任的工作角色,如投擲彈藥、拋灑干冰、運輸貨物等,極易引起質量和慣量的變化。這不僅影響單個無人機的工作狀態,影響時延狀態觀測器的收斂性,而且影響編隊的全局控制性能。文獻[9]利用非線性自適應控制對未知定常參數進行辨識;文獻[10]基于自適應反步法和非線性阻尼算法,提出了一種魯棒自適應控制器,實現了對慣量參數的估計,最終實現了航天器姿態控制系統全局一致有界;文獻[11]針對具有未知常數慣量不確定性和外界干擾的航天器,設計了一種有限時間自適應滑模姿態跟蹤控制器,使得期望姿態實現有限時間一致;文獻[12]針對機械系統高頻扭矩振動帶來的系統慣量變化,采用抗共振濾波器和自適應神經控制器的協同作用解決了這一問題。以上文獻中,系統質量和慣量多為未知定常,或僅有其一發生變化的情況,然而這兩者往往是密不可分的;同時,在依據李雅普諾夫函數法設計控制律時,將待估計值處理為緩變量,只適用于部分場景,適用范圍較小。

本文針對上述兩個方面的問題,采用領航跟隨法的編隊方式,應用編隊參數生成虛擬無人機位置,然后根據編隊誤差,設計基于時延觀測器的旋翼無人機自適應編隊控制器。在通信存在變時延的情況下,跟隨者可以準確跟蹤虛擬無人機位置,實現對各類變慣量行為的自適應調整,提高編隊收斂速度和精度。設計2組仿真實驗,通過跟蹤不同路徑和慣量變化方式,驗證所提方法的有效性。

1 模型與問題描述

1.1 模型描述

根據牛頓歐拉建模原理,參考文獻[13],建立四旋翼無人機系統的動態模型

(1)

(2)

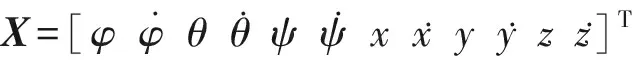
該模型遵循如下假設:

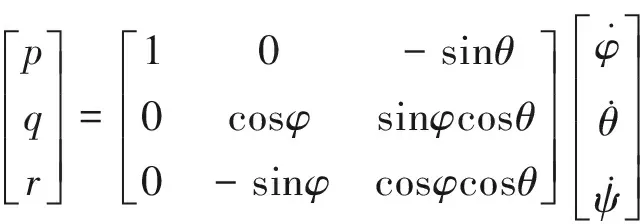
(3)

式中:p、q、r分別為機體坐標下的滾轉、俯仰、偏航角速度。

由于四旋翼無人機通常做小角度運動,可利用小角度近似得

(4)

(2)四旋翼的結構是剛性且對稱的。

(3)四旋翼質心與機體坐標系原點一致。

需要說明的是,由于四旋翼無人機欠驅動的特點,不可能對輸出ξ中的6個自由度都進行控制。一種合理的方案是:控制質心位置[xyz]T和偏航角ψ,同時保證另外兩個歐拉角[φθ]穩定有界。

1.2 問題描述

在領航跟隨法中,領航者沿著預先設定好的路徑行進,跟隨者則需要獲得領航者的位置和角度信息,結合自身位姿進行控制。編隊的主軌跡通常由領航無人機Rl決定。跟隨無人機Rf的參考軌跡由領航無人機和結構參數生成的虛擬無人機Rv軌跡決定。一個典型的三角形編隊如圖1所示,編隊拓撲圖見圖2,圖中所有無人機具有相同的運動學模型。

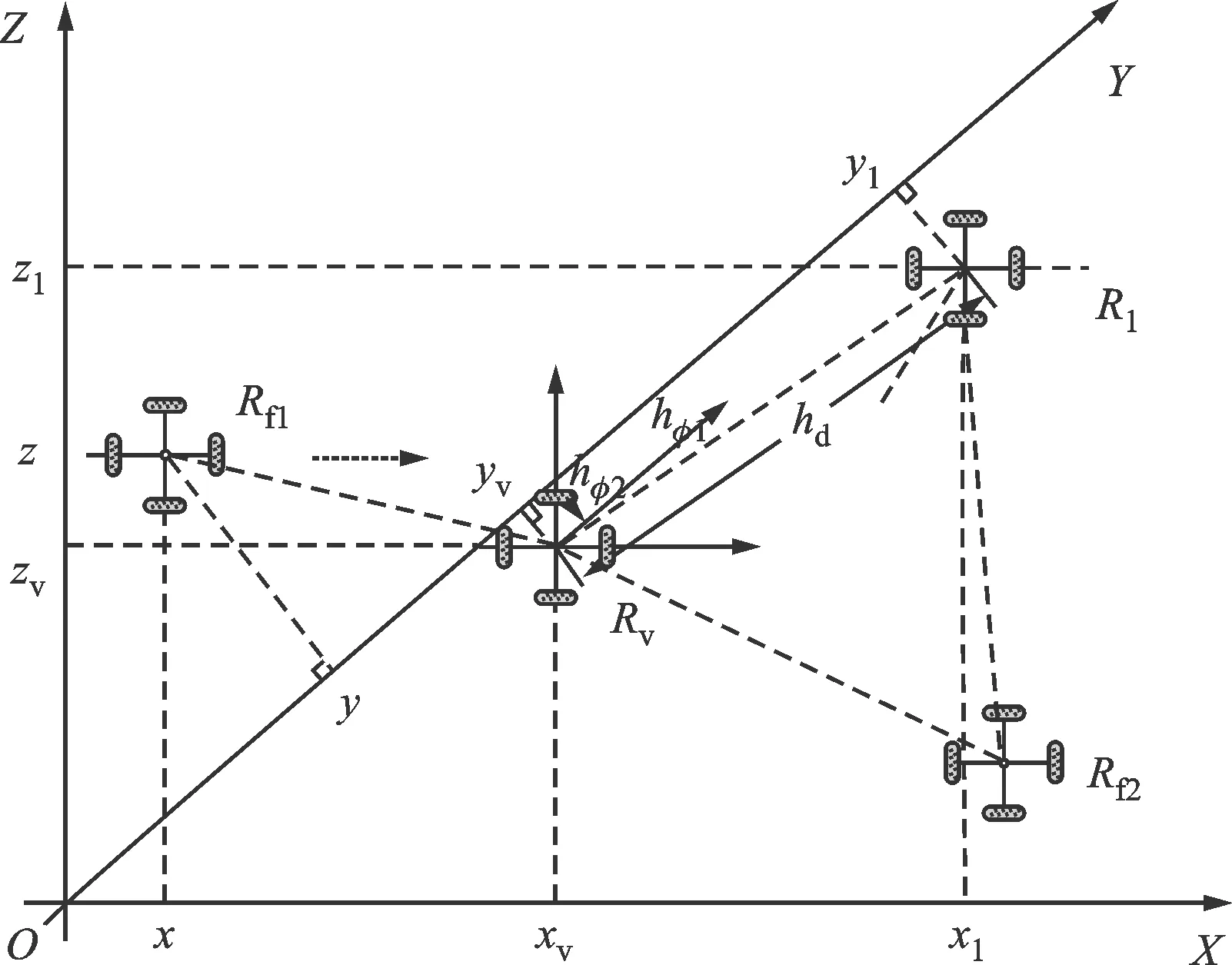
圖1 三角形編隊圖

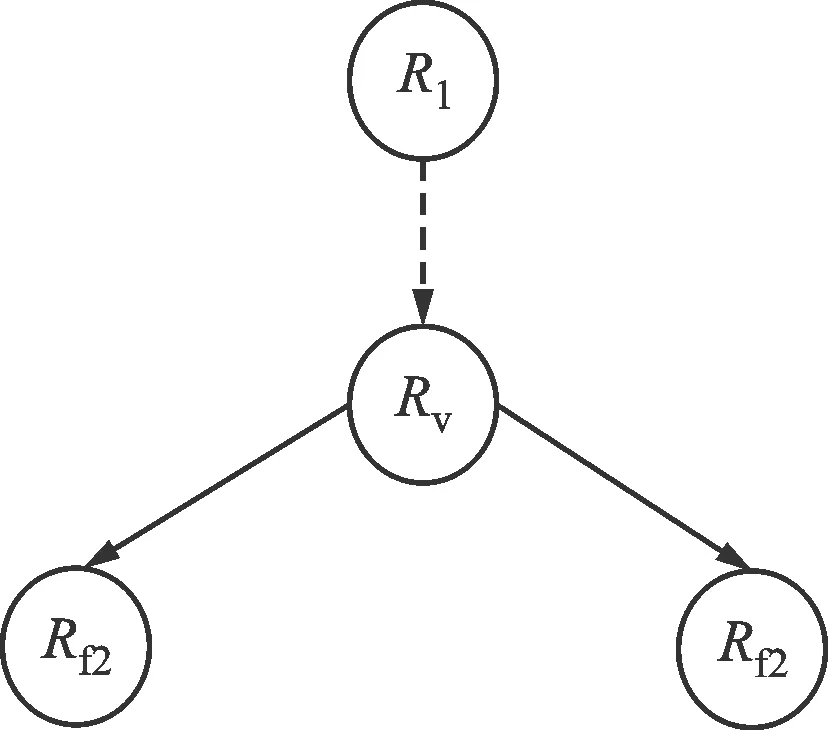
圖2 編隊拓撲圖

從一致性的角度分析領航跟隨編隊系統。定義控制目標ξ=[xyzψ]T,多智能體系統被稱作滿足一致性,當存在一個向量函數ci(t)∈Rn時,對第i個無人機有

(5)

式中:i∈{f1,f2};

被稱作一致參考函數,表示一個基于三維極坐標的虛擬無人機的位置;h(t)=[hd(t),hφ1(t),hφ2(t)]∈R3為分段連續可微的時變編隊信息,hd、hφ1、hφ2分別表示虛擬無人機與領航者的編隊距離、水平方向夾角以及垂直方向夾角。

從控制的角度來看,即Rf1與Rf2在歐拉坐標系下,通過尋求適當的控制器ui(i=1,2,3,4)完成對位姿誤差e(t)=ξi(t)-ξvi(t)的跟蹤,使得e(t)漸近穩定。這樣,領航跟隨法下的編隊控制問題就轉化成了跟隨無人機Rfi對虛擬無人機Rvi的位置姿態ξvi(t)=ci(t)的跟蹤問題。這種考慮適用于小型編隊,主要采用集中控制的方式進行通信,運算量較小。

在編隊過程中,受通信條件、設備負載以及無人機系統自身存在時延等情況的限制,領航者的部分輸出信息

{x1[t-δ(t)]y1[t-δ(t)]z1[t-δ(t)]

ψ1[t-δ(t)]}T=ξ1[t-δ(t)]

(6)

式中:δ(t)∈[0,Δ]為已知有界時變時延信號。

此時,跟隨者無法準確獲取領導者的實時位置信息。當時延大于一定閾值時,可能會出現跟隨者無法有效跟蹤、編隊隊形發散的情況。針對這種情況,本文提出一種時延狀態觀測器設計方法。

2 時延狀態觀測器設計

2.1 可觀性分析

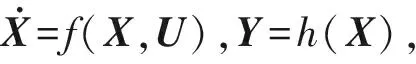
Σ是弱可觀的,當且僅當對于1≤p≤m,觀測矩陣

(7)

是滿秩矩陣。

為了計算Om的秩,引入向量場h關于向量場f的李導數Lfh(X)

(8)

(9)

(10)

據此可以一步步構造出一組n=12的線性無關向量組,它是由輸出向量的李導數及其梯度的所有有限線性組合得來的。第一個得到的線性無關向量組為

(11)

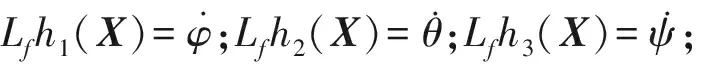
可得

(12)

由det(Om)=-1可知,矩陣Om是滿秩的。由此可以得出,該系統是弱局部可觀的。

2.2 觀測器選擇

基于2.1節的分析,針對系統

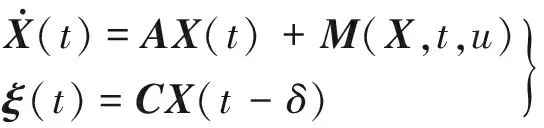
(13)

式中:C為輸出矩陣;

設計如下觀測器

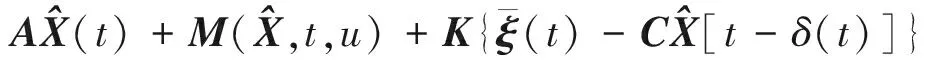
(14)

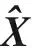
引理1[8]若形如式(13)的系統符合

(1)M(X,t,u)滿足利普希茨連續條件,

(2)時變時延δ(t)∈[0,Δ]有界,

則有

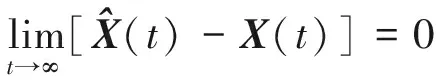
(15)

證明:對本文采用的旋翼無人機系統模型而言,設

則

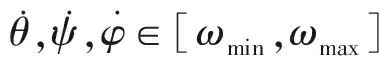
有界,M21滿足利普希茨連續條件,記為L=L21。

由于M(X,t,u)各元素偏導數均有界,不失一般性,M(X,t,u)滿足利普希茨連續條件,L=max(Lij),i∈{1,2},j∈{1,2,3}。

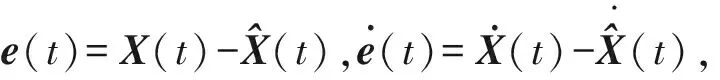
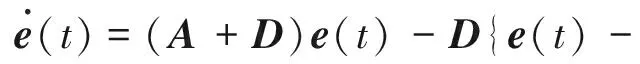
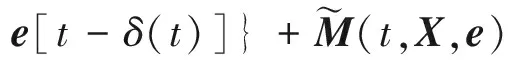
(16)

式中:D=-KC;

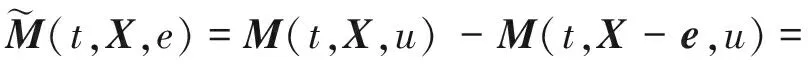
M(t,X,u)-M(t,X,u)

(17)

當t>Δ時,有

e(t)-e[t-δ(t)]=

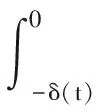
(18)

將式(18)代入式(16)中,得

(19)

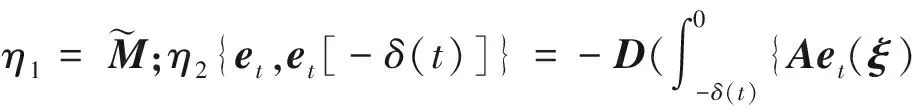
選取李雅普諾夫函數

V=eTPe

(20)

可得

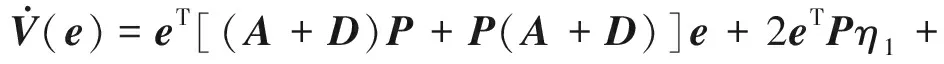
(21)

由文獻[16]中定理1可得

(22)

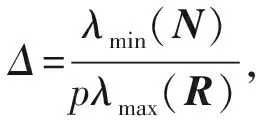
(23)

證畢。在該觀測器中,

為使其滿足赫爾維茨定理,根據分塊矩陣的性質,|A-KC|=|A1‖A2‖A3‖A4‖A5‖A6|,有

λ(A-KC)=
λ(A1)∪λ(A2)∪λ(A3)∪λ(A4)∪λ(A5)∪λ(A6)

(24)

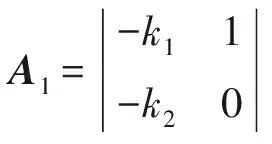
(25)

由(λ+κ)2=0可得λ2+2κλ+κ2=0,κ>0,從而

k1=2κ;k2=κ2

(26)

進一步組合可求得K。通過參數整定可以得出,當κ=0.6時,觀測器經過短暫的調整,可以很好地獲得通信延遲下的虛擬領導者位置,為自身提供準確的目標點。同時需要注意的是,此類觀測器設計時要求被觀測者的精確模型,而無人機工作時,往往帶有拋灑、投擲等變質量、變慣量的行為。為此需要一類具有自適應能力的控制器,以適應此類系統變化,并為觀測器提供相對準確的質量與慣量變化。

3 控制器設計

定理1考慮四旋翼系統動態模型如式(1)～式(2)所示,設計控制律

(27)

(28)

(29)

(30)

組成閉環控制系統,則閉環系統漸進穩定。其中

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

(47)

證明:以滾轉通道為例,

(48)

可以重構為

(49)

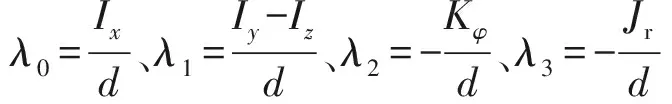
(50)

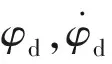
(51)

選取一個候選李雅普諾夫函數

(52)

(53)

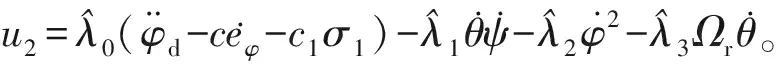
(54)

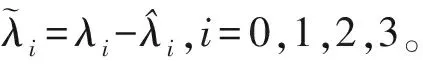
(55)

(56)

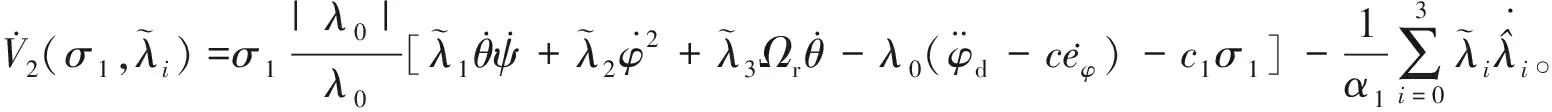
(57)

(58)

(59)

(60)

代入V2,由此可得

(61)

綜上,在該控制器作用下,φ的漸進穩定性得到證明。考慮本文設計的其余滑模函數σi和控制器ui,其余通道的穩定性證明可按照相同思路進行,取李雅普諾夫函數

(62)

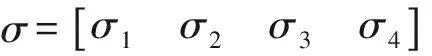
(63)

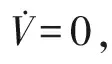
4 仿真驗證

為驗證觀測器及自適應算法的收斂性和趨近律的有效性,本節選擇MATLABR2017a搭建仿真模型。實驗以森林滅火為背景,測試跟隨無人機在完成編隊任務的同時投擲碘化銀增雨焰條和均勻噴灑干冰的控制效果。仿真初始參數設定如表1所示。

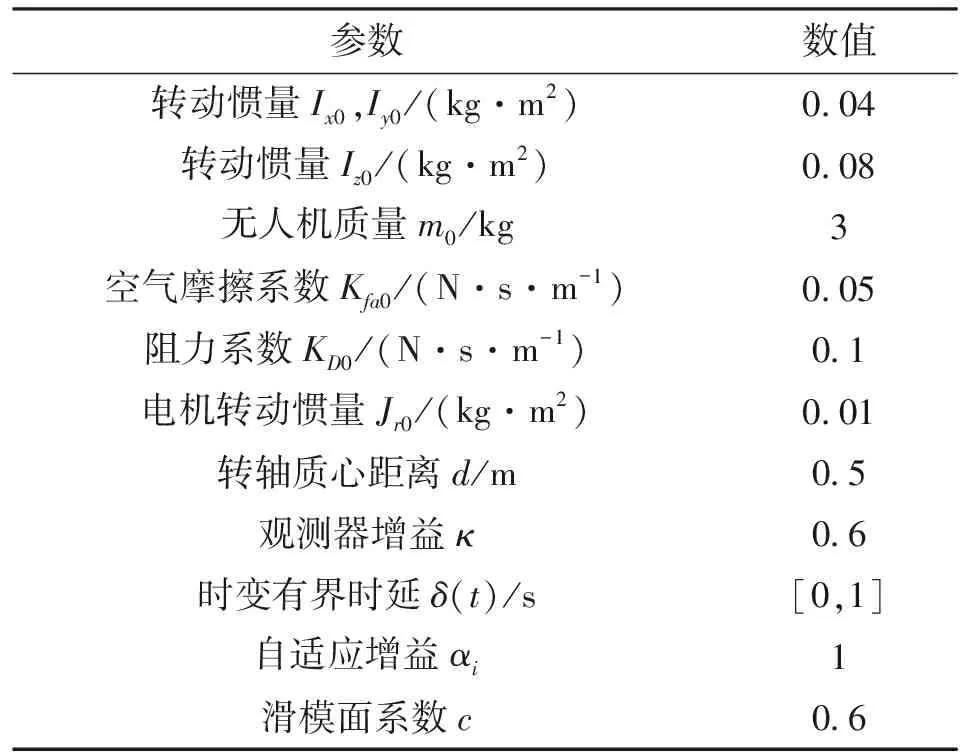
表1 仿真初始參數

4.1 持續勻速噴灑的螺旋線跟蹤

虛擬無人機軌跡選取螺旋線方程,表達式為Pd=[0.5cos(0.5t)0.5sin(0.5t)2+0.1t]。設無人機質量m=(3-0.03t) kg;轉動慣量Ix=Iy=(0.04-0.000 6t) kg·m2,Iz=(0.08-0.000 6t) kg·m2;時變有界時延函數δ(t)∈[0,1];dFx=0.1sin(0.1πt),dFy=0.1cos(0.1πt),dFz=0.2cos(0.2πt)為各向擾動。仿真結果如圖3～圖7所示。

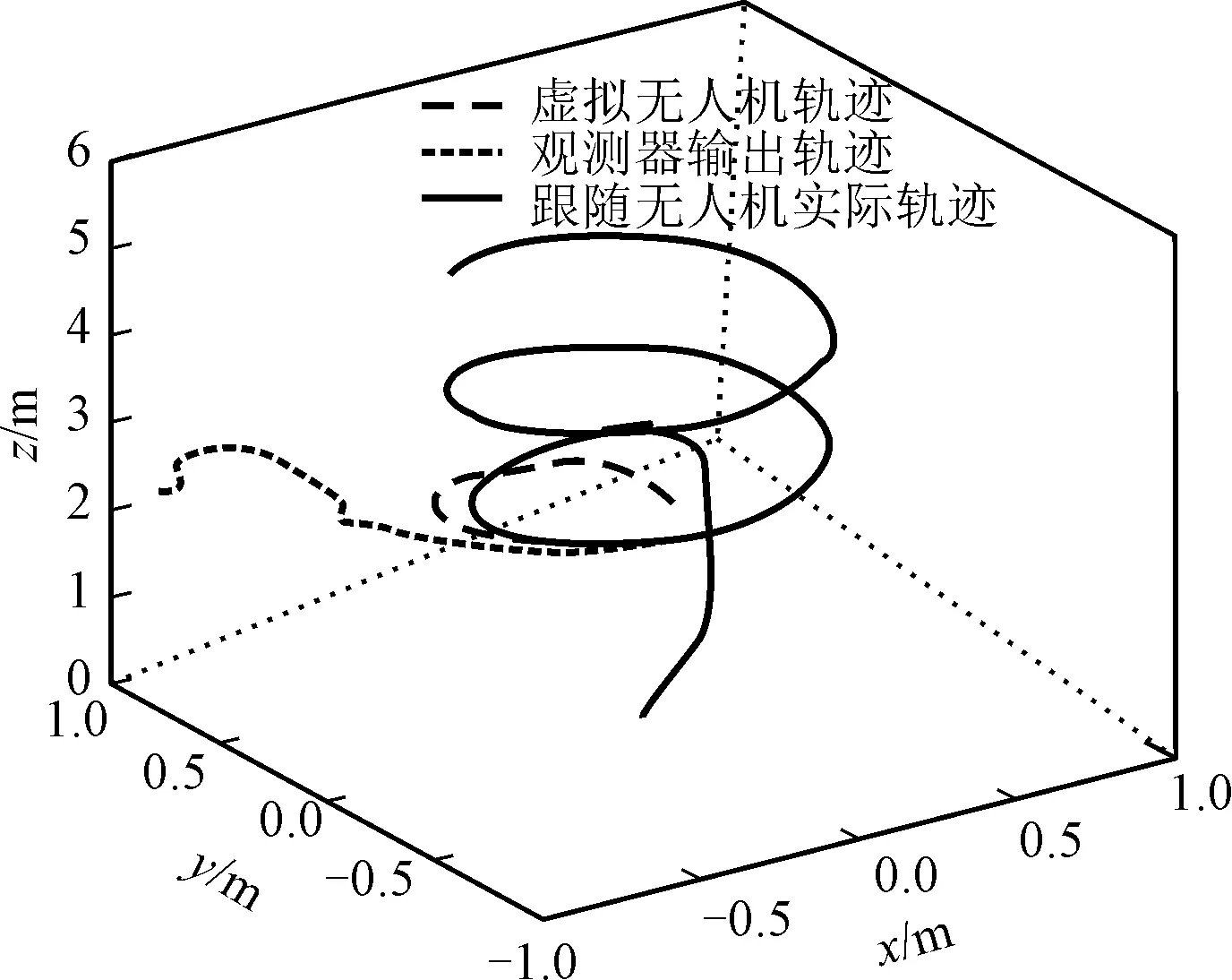
圖3 螺旋線跟蹤位置變化

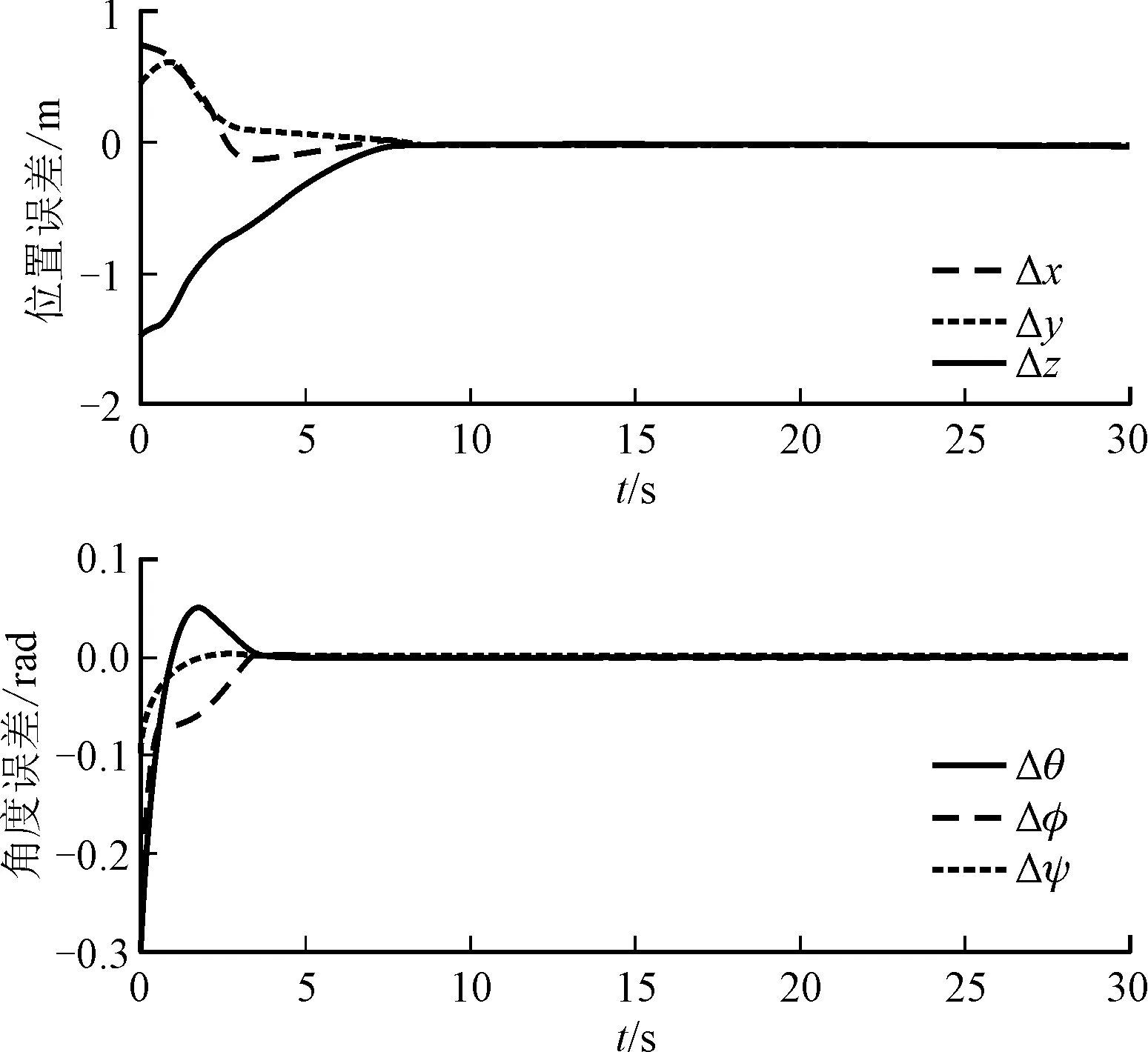
圖4 位姿觀測誤差

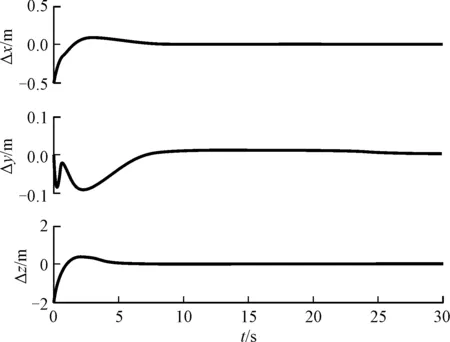
圖5 位置跟蹤誤差

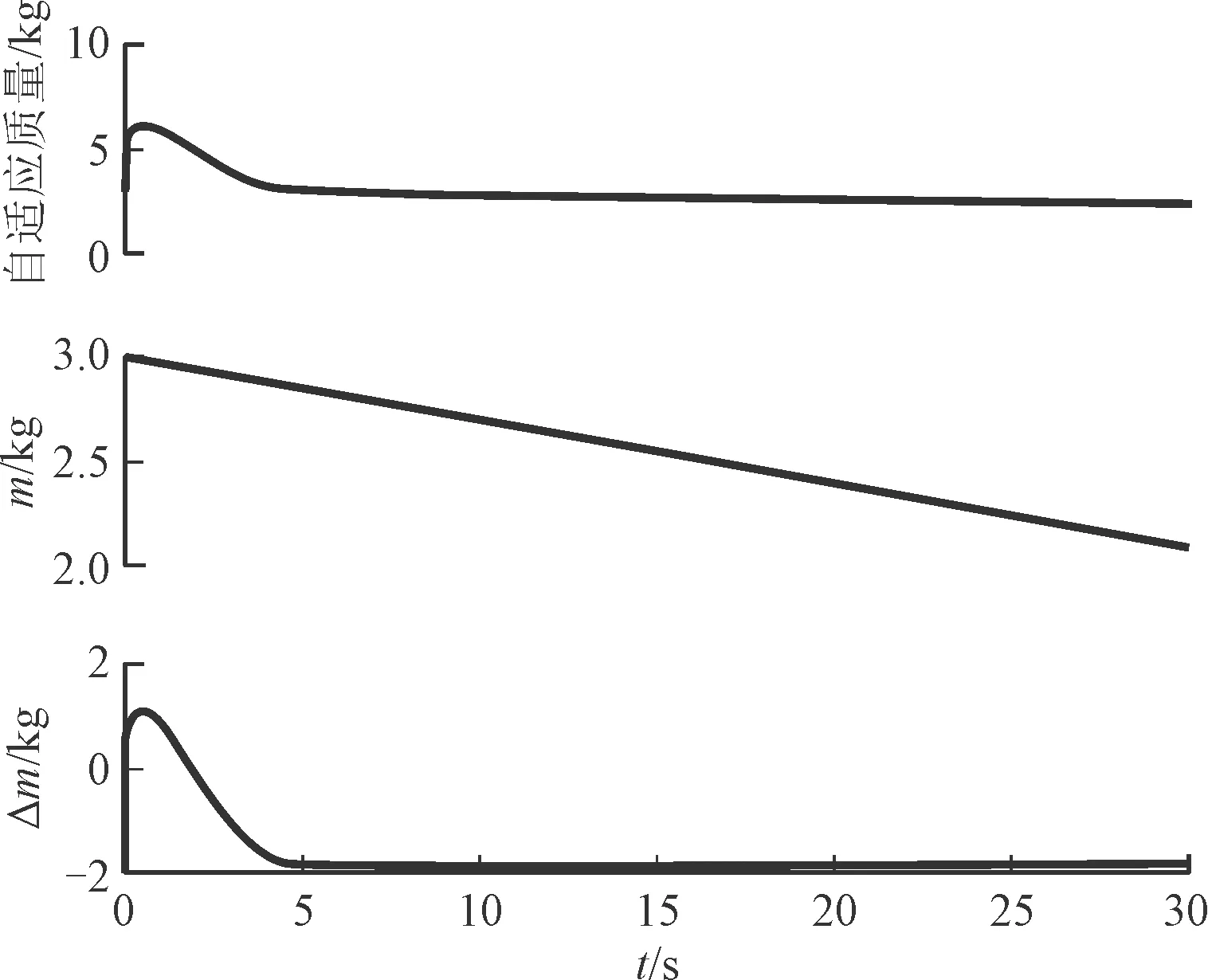
圖6 質量自適應值

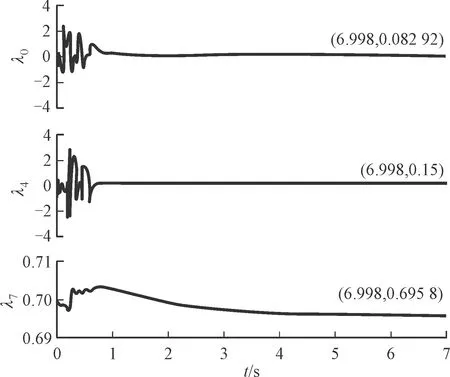
圖7 部分系數自適應值

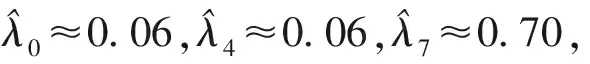
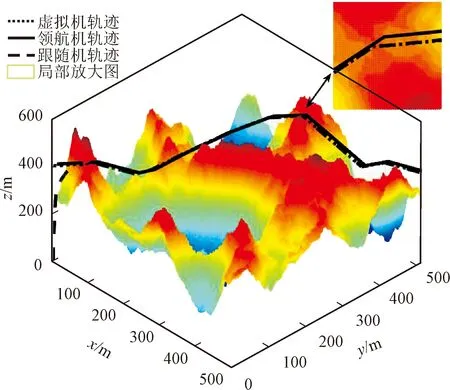
圖8 山區路徑跟蹤圖

4.2 間斷投擲的山區路徑編隊飛行

選取桂林(110.61°E,25.07°N)處的高度值繪制如圖8所示地形,面積為512×512 m2。為驗證間斷投擲時控制器對質量階躍變的適應能力,選取m0=3 kg,每隔6 s拋下一個Δm=0.5 kg的增雨焰條,共計i=5根,轉動慣量Ix=Iy=0.04 kg·m2不變,Iz0=0.08 kg·m2且每次下降0.005 kg·m2。其他參數設定與4.1節相同,結果見圖8～圖11。

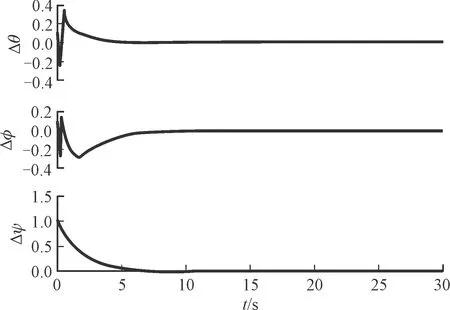
圖9 姿態跟蹤誤差

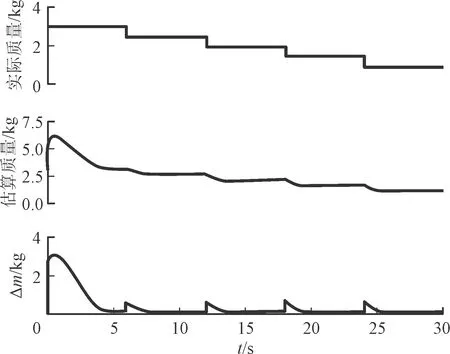
圖10 質量自適應值圖

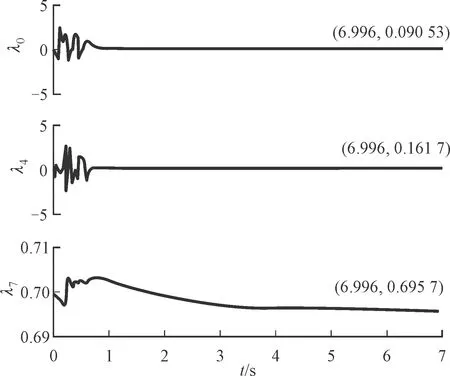
圖11 部分系數自適應值

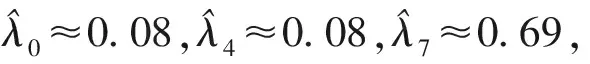
從以上兩組仿真可以看出,利用本文所提方法,在變時延存在下的情況下,無人機偏隊對于變質量變慣量行為具有良好的控制能力,編隊誤差快速收斂至0,且未出現時間滯后現象。

5 結論與展望

本文提出了一種基于時延觀測器的旋翼無人機自適應編隊控制方法,在領航跟隨法的基礎上,抑制無人機編隊中的通信時延與工作引起的慣量變化。基于無人機系統動力學模型設計了變時延狀態觀測器,對領航無人機狀態進行觀測和補償。在補償后的被控對象基礎上,設計了自適應滑模控制器,對變負載工作狀態下的質量和慣量進行估計。仿真結果表明該方法對變時延和變慣量條件下的編隊控制有較強的魯棒性。

本文選擇領航跟隨法進行編隊驗證是基于其原理簡單、便于實現的特點。下一步擬將時延觀測器的設計方法與基于一致性的編隊方法相結合,彌補其被動式收斂的不足,提高控制精度和速度。