考慮齒輪形變的諧波減速器齒廓優化方法

張寧,張英杰,李陽帆

(西安交通大學機械工程學院,710049,西安)

1955年,美國工程師Musser基于彈性動力學原理設計了諧波減速器,由于其具有質量小、傳動比大、結構簡單、傳動精度高等優點,被廣泛應用于航空航天、機器人、軍事裝備、精密光學設備等新興技術領域[1]。諧波減速器一般在低速低轉矩工況下運轉,主要失效形式是輪齒的疲勞斷裂,因此針對諧波減速器齒廓的設計與改進至關重要,不僅可以提高諧波傳動系統的承載能力,而且可以提高諧波減速器的運行平穩性以及可靠性[2]。

目前,在齒形設計方面的研究側重點是加大嚙合齒面的長度以提高承載能力。諧波減速器主要的齒廓類型包括漸開線齒廓、S形齒廓和雙圓弧齒廓等[3-4]。漸開線齒廓由于在空載時期同時嚙合的齒數較少,大多數嚙合輪齒處于邊緣嚙合狀態,不利于齒間油膜的形成,并且共軛運動的發生區間狹小,使得傳動的動態性能降低。圓弧齒廓由于在運動過程中能保持柔輪與鋼輪輪齒持續接觸,使得同時嚙合的齒數增加,共軛區域增加,提高了承載能力以及扭轉剛度[5]。S型齒廓與雙圓弧齒廓比相對漸開線齒廓承載能力更高,傳動更加平穩,目前應用廣泛。

與一般齒輪傳動不同,波發生器裝配進入柔輪后,柔輪會產生一定程度的彈性形變,形變后柔輪內表面與波發生器的外表面緊密貼合,由于在傳動過程中,柔輪齒圈每個位置的形變是動態變化的,這就可能導致輪齒產生嚙合干涉或者柔輪脫離嚙合[6]。為了計算簡便,將柔輪中性層的形變近似作為柔輪的形變,從而對齒形進行設計優化[7]。

在設計中需要考慮諧波減速器的嚙合側隙。許多研究以減小側隙為目標對于齒廓進行優化[8],合理的初始嚙合側隙有利于提高傳動平穩性、減小傳動沖擊[9]、提高承載能力[10]、避免滯回[2-11]以及提高傳動效率[12]。但是柔輪不是剛體,在形變過程中齒廓線齒頂形變量與齒槽形變量以及柔輪內表面形變量不同,若不考慮變形差而使用統一的形變規律,必然會造成實際與理論計算的輪齒嚙合位置出現偏差,進而影響初始側隙的大小。

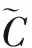
柔輪在裝配過程中不僅會引起柔輪中性層的形變,還會導致柔輪齒廓形狀的改變。對于尺寸小,傳動精度高的精密器械,設計時忽視這種形變會使得最終輪齒側隙與設計不符,從而對傳動的平穩性造成影響。

通過建立柔輪的裝配后的形變模型,利用殼體理論分析齒圈受力與形變量情況,提出一種新的柔輪齒廓設計優化思路。以雙圓弧齒廓為例,采用有限元軟件量化分析齒廓裝配形變,計算柔輪輪齒的實際齒廓線位置,對齒廓線方程進行修正,與原齒廓的嚙合情況進行對比分析,進而論證了該方法的有效性及合理性。

1 建立柔輪形變分析模型

1.1 柔輪端面的形變分析

在諧波齒輪傳動中,一般采用剛輪固定、波發生器輸入、柔輪輸出的傳動方式。由于波發生器凸輪長軸大于柔輪內徑,所以裝配后波發生器與柔輪過盈配合,柔輪形狀發生形變,柔輪端面變化如圖1所示。

柔輪裝配形變后半徑可以表達如下

r=rb+ω(φ)

(1)

式中:rb為未形變時柔輪中性層半徑;ω(φ)為柔輪各點裝配后的形變。不同波發生器表達式不同,本文以余弦凸輪波發生器為例,形變后表達式為

r=rb+ω0cosφ0

(2)

式中:ω0為柔輪最大形變;φ0為與波發生器長軸夾角。

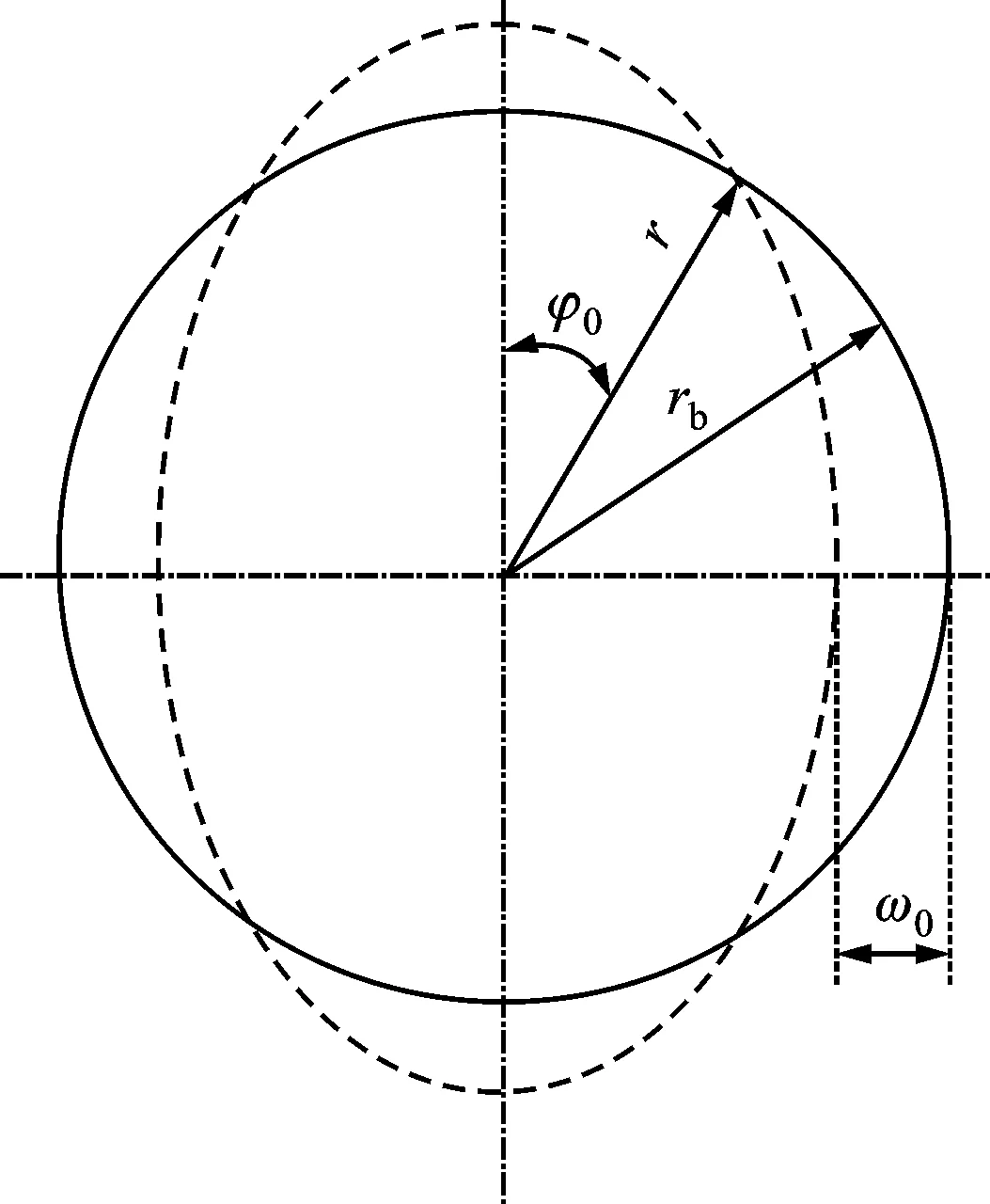
圖1 柔輪裝配形變圖

1.2 柔輪形變對齒圈截面形變的影響

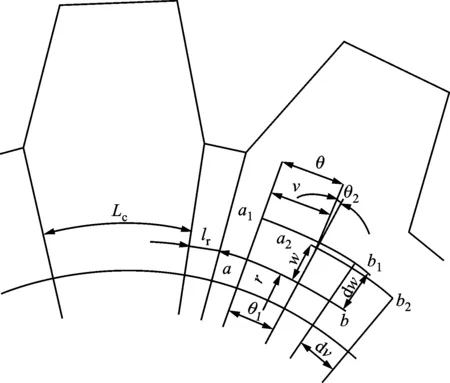
圖2 柔輪中線線元位移

當波發生器裝入柔輪后,柔輪齒廓受徑向力與切向力共同作用[14-15]。如圖2所示,ab為形變前齒圈截面內任意曲線單元,柔輪形變的過程可以分解為ab沿徑向位移dw至a1b1,以及a1b1沿切向位移dv至最終位置a2b2,則兩次的形變量分別為

a2b2-ab=(r+w)dφ0-rdφ0=wdφ0

(3)

a1b1-a2b2=v+dv-v=dv

(4)

根據線元長度不變的基本假設,有

dv+wdφ0=0

(5)

根據圖1,法線轉角為

θ=θ1-θ2

(6)

將θ1=v/r、θ2=dw/rdφ0代入式(4),結合式(5)(6)得到θ角的變化量

(7)

式中:p為齒輪周節。

如圖2所示,將輪齒的每一個齒距分為齒頂部分lc以及齒根部分lr,則柔輪彈性形變后兩段對應的角度增量分別為Δθc、Δθr,對應齒高分別為hc、hr。截取足夠小的寬度d,將柔輪輪齒齒頂、齒根到柔輪內表面的范圍視作矩形,根據慣性矩公式I=dh2/12,可計算出齒頂、齒根部分慣性矩Ic、Ir。設ks為齒根厚系數,則有

(8)

根據殼體理論,當殼體純彎曲時,有

(9)

σ∝Δθ/l

(10)

式中:σ為殼體內周向應力。

根據胡克定律,齒圈應變有

ε=σ(φ0)/E

(11)

式中:E為材料的拉壓剛度。

聯立式(8)～(11),可以得到

(12)

式中:εc為齒頂部分形變;εr為齒根部分形變。

由式(12)可以看出,在簡化后的齒圈模型中齒頂所受內應力大于齒槽部分,受力彈性形變方面齒頂也要略大于齒槽部分。由此可知,柔輪形變時,輪齒的齒頂形變量與齒根處形變量不同,由于在實際裝配中,齒廓形狀復雜,殼體并非純彎曲,且殼體內各層相互擠壓,會對齒廓產生復雜影響。針對此問題,本文提出采用有限元法分析齒廓裝配形變,在設計時對原有齒廓形狀進行補償的設計思路。

2 雙圓弧切線共軛齒廓線求解

柔輪雙圓弧齒廓如圖3所示。齒廓線由兩段圓弧以及一段直線BC組成,為方便描述,局部坐標系Sf(O1,X1,Y1)定義如下:X1為柔輪中性層切線;Y1為齒廓對稱線[15]。

ha:齒頂高;h:全齒高;Ya:凸圓弧齒廓圓心徑向偏移量;la:凸圓弧齒廓圓心水平偏移量;Yf:凹圓弧齒廓圓心徑向偏移量;δL:齒型工藝角;ρa:凸圓弧齒廓半徑;ρf:凹圓弧齒廓半徑;lf:凹圓弧齒廓圓心水平偏移量圖3 柔輪雙圓弧齒廓

基于圖3的描述,以齒廓弧長s為基本參數,對3段齒廓函數描述如下。

AB段齒廓函數表達式如下

(13)

式中:s∈(0,l1),l1=ρa(αa-δL),αa=arcsin((ha+Ya)/ρa);xs=-la;ys=h-ha+ds-Ya。

BC段齒廓函數表達式如下

(14)

式中:s∈(l1,l2),l2=l1+(ρa+ρf)tanδL。

CD段齒廓函數表達式如下

(15)

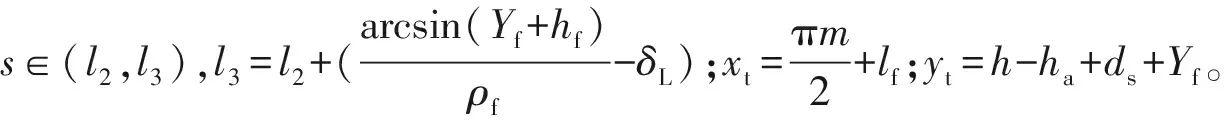
為方便表示,令

(16)

考慮到柔輪中性線單元的移動以及齒廓線的彈性形變,對原齒廓進行修正

(17)

式中:F(s)代表齒廓因柔輪中性層位移而造成的位移,表示如下

F(s)=[wsinφvcosφ0]

(18)

G(s)表示齒廓因受內力而造成彈性形變,與柔輪幾何形狀、材料等因素有關。

根據諧波傳動的包絡法求解出共軛齒形

Xc=MXf

(19)

式中:共軛矩陣M的表達式為

(20)

其中rm為形變后齒廓的徑向長度,φf為柔輪未形變端轉角,φ為柔輪中性層垂線與坐標系法線夾角。

3 裝配仿真實例驗證

3.1 柔輪裝配體三維模型建立及有限元分析

以某8型諧波減速器為例,z1=160,z2=162。模數m=0.32。諧波減速器三維模型以及柔輪結構部分尺寸參數如圖4、圖5所示。

圖4 諧波減速器三維模型

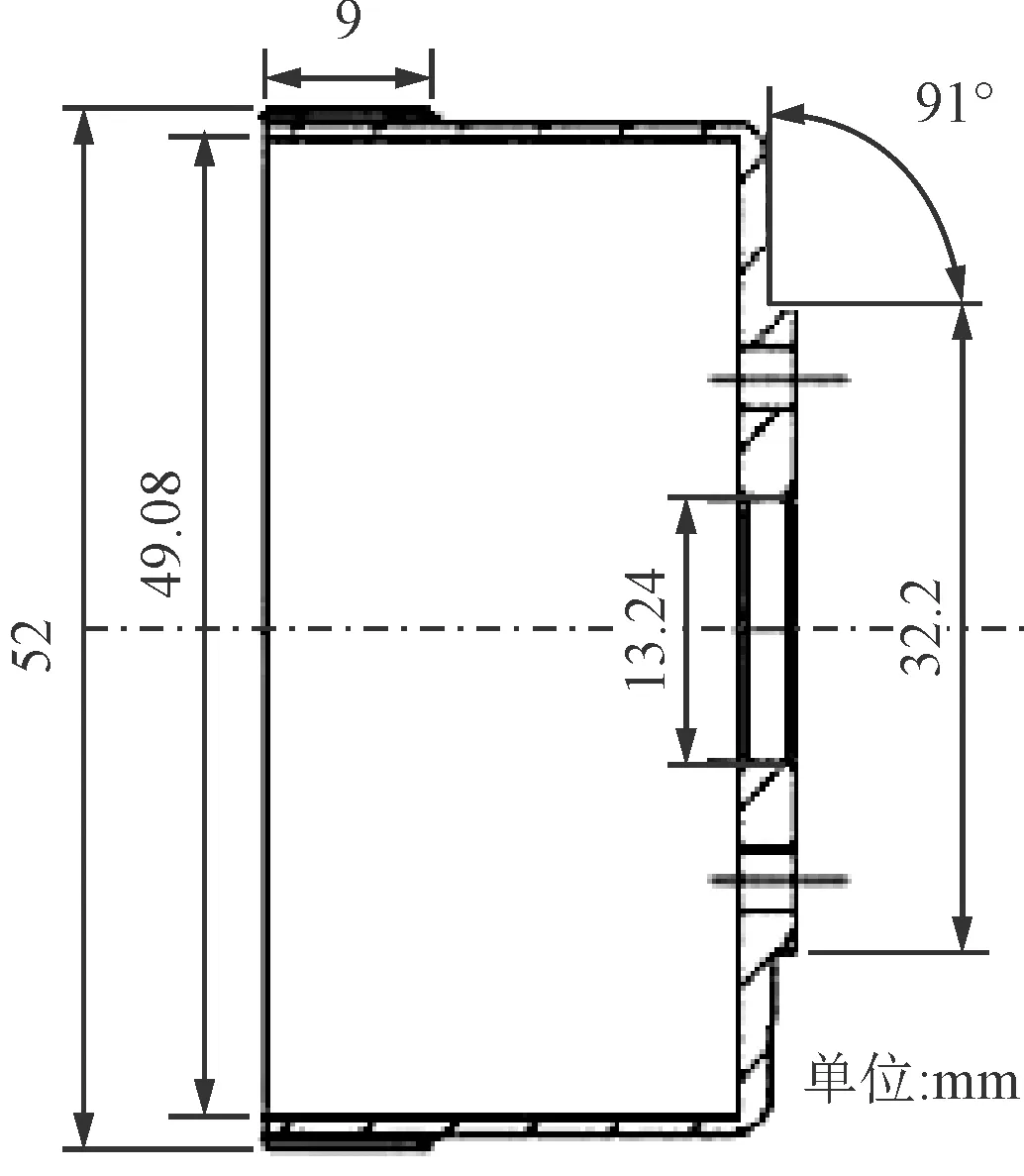
圖5 柔輪結構部分尺寸示意圖

采用Ansys軟件對裝配過程進行仿真分析。柔輪采用工業中諧波減速器常用的20Cr2Ni4合金鋼材料,楊氏模量E1=2.06×105MPa,泊松比γ1=0.3;剛輪采用45號鋼材料,楊氏模量E2=2.10×105MPa,泊松比γ2=0.31。

對于Ansys軟件分析過程做出如下處理:①由于波發生器的材料硬度遠高于柔輪,故將波發生器視為剛體;②諧波減速器一般的傳動形式為輸出軸連接柔輪,因此對于柔輪安裝軸處施加固定約束;③由于諧波減速器為環形對稱結構,為簡化計算,取諧波減速器整體模型的1/2,對波發生器施加位移約束完成裝配過程。

3.2 有限元分析結果

通過Ansys軟件仿真分析,柔輪在裝配后發生形變。柔輪整體仿真實驗形變量如圖6所示,可以看出,在柔輪長軸處形變量最大,因此本文著重對長軸處的齒廓線進行研究。

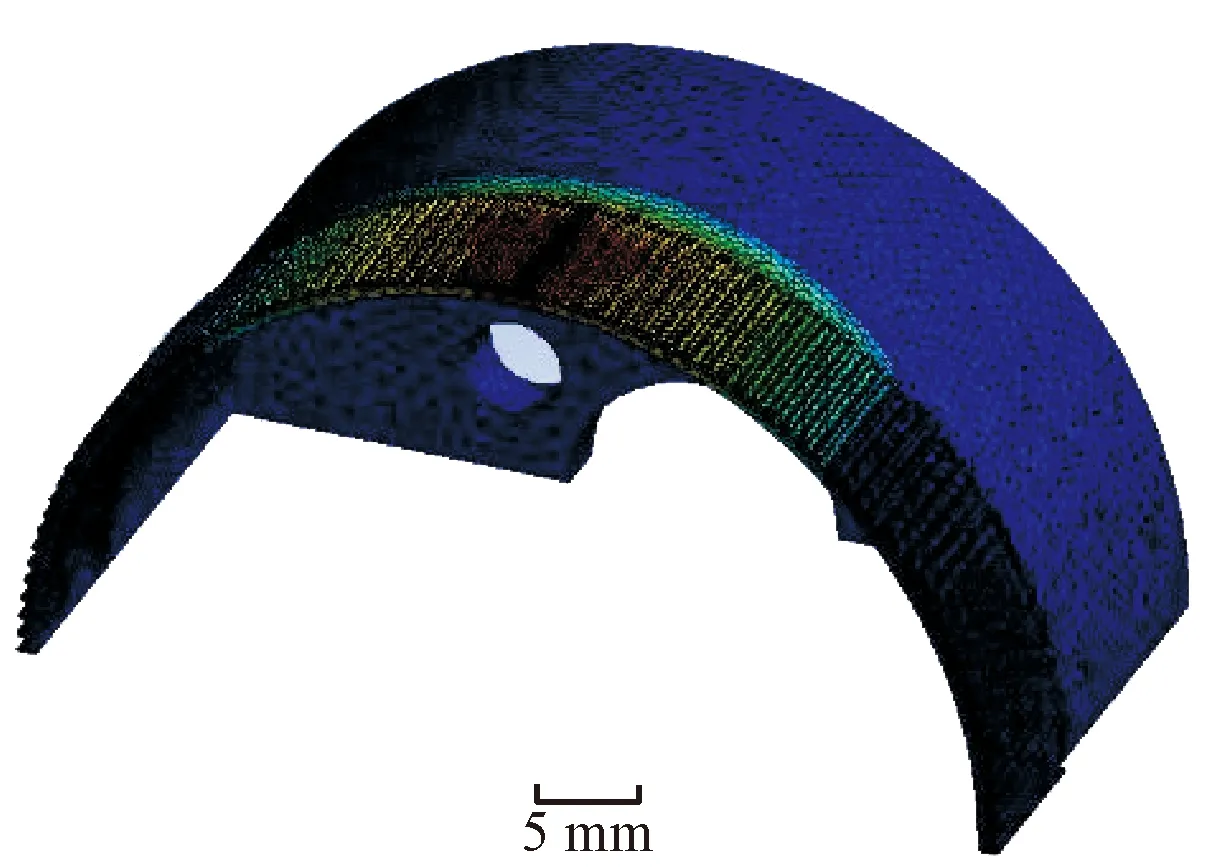
圖6 柔輪整體仿真實驗形變量

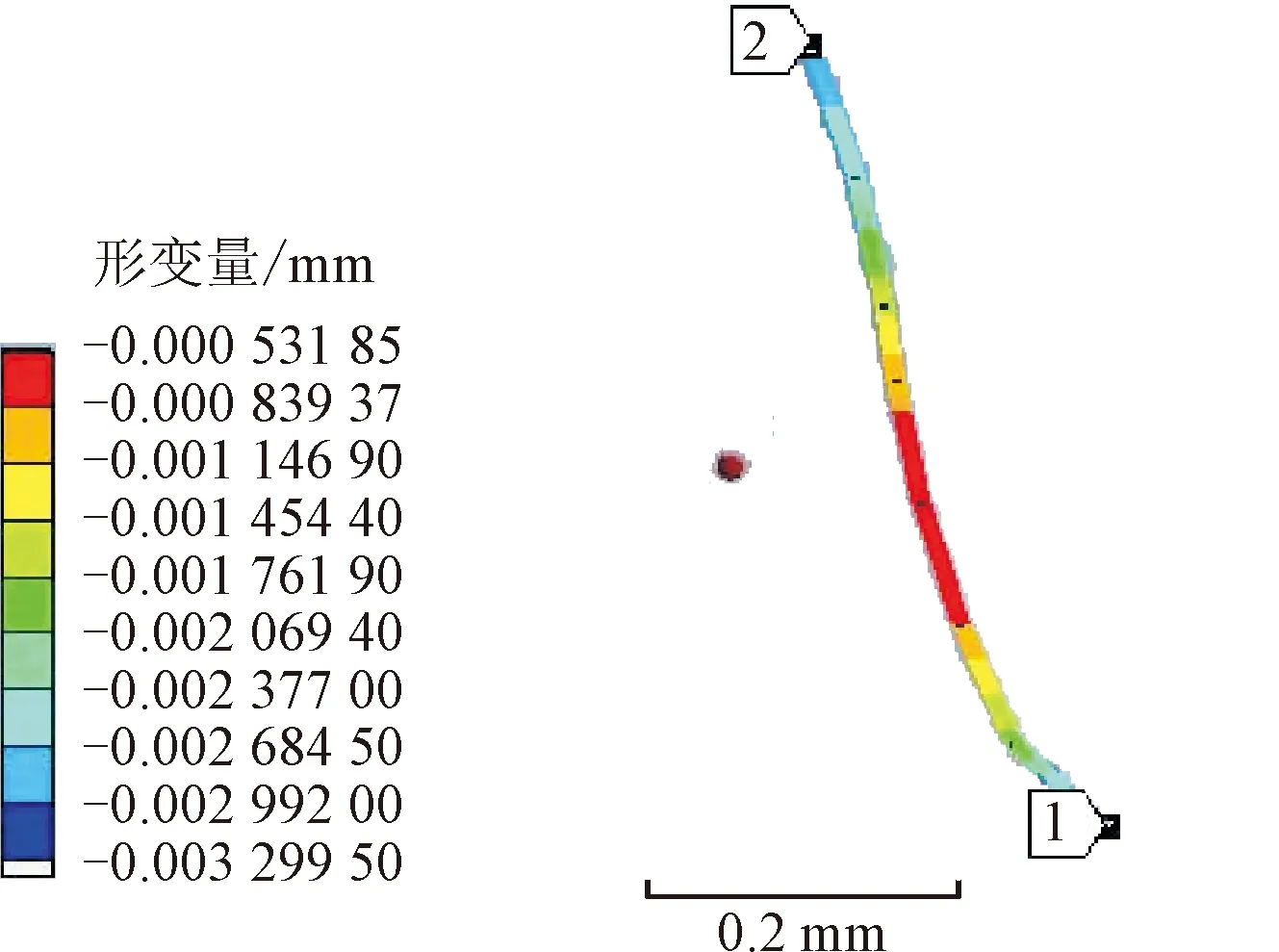
圖7 柔輪齒廓線單側齒廓在裝配過程中x方向齒廓形變量

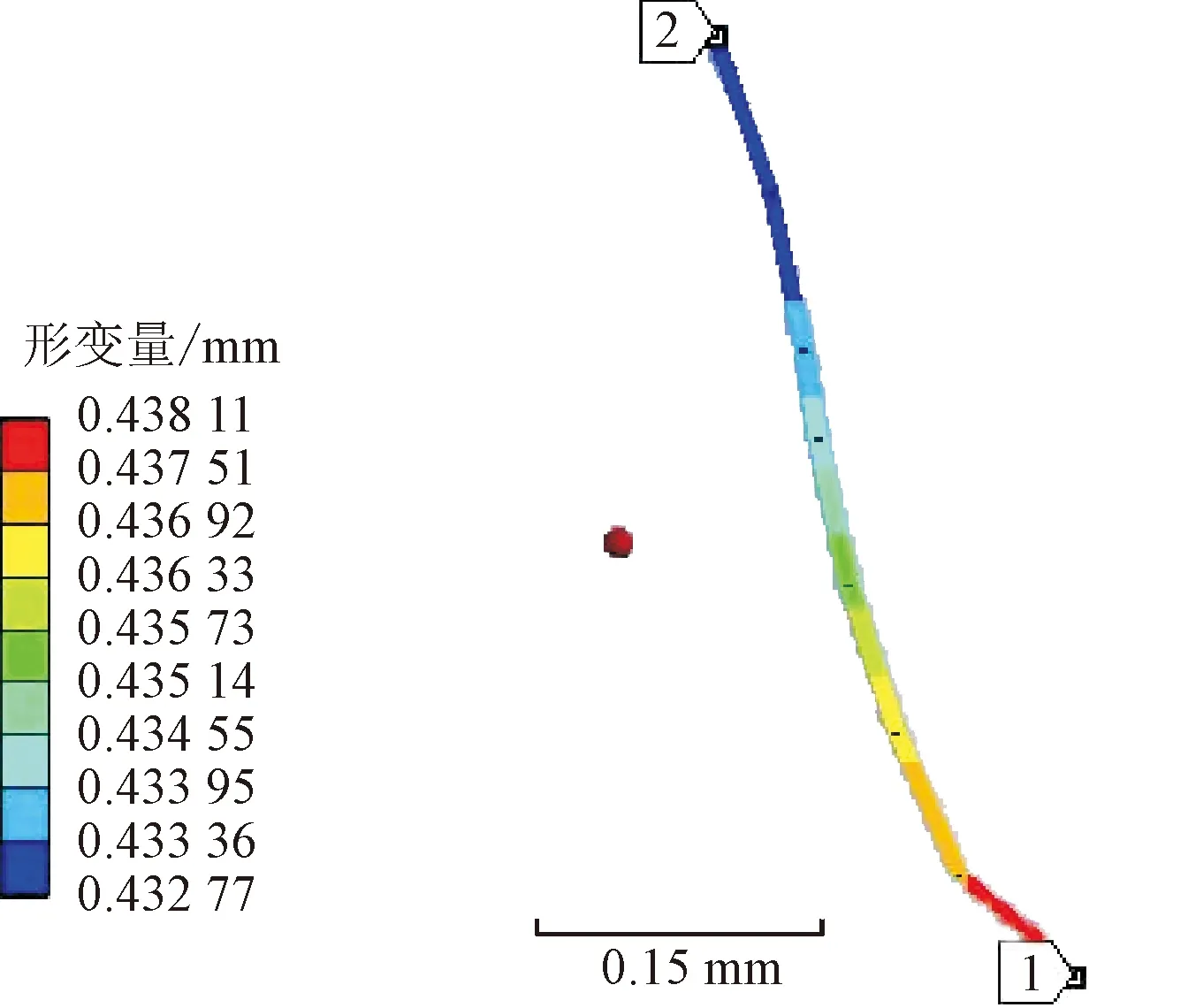
圖8 柔輪齒廓線單側齒廓在裝配過程中y方向齒廓形變量

圖7與圖8分別給出了柔輪齒廓線單側齒廓在裝配過程中x方向與y方向的形變量。可以看出,x方向齒廓形變較小,y方向齒廓形變較大,位于齒根的齒廓形變量明顯大于位于齒頂的齒廓,齒根與齒頂存在變形差,從而進一步驗證了本文的結論。

由于變形差的存在,使得諧波減速器裝配后,柔輪齒廓線的實際位置與理論位置存在差異,影響輪齒嚙合效果,因此諧波減速器的齒形需要進行優化。根據Ansys軟件計算的離散變形數據,齒廓弧長s與仿真得到的形變量σ近似呈二次函數關系。采用Matlab軟件擬合得到方程

(21)

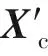
圖9 齒廓位置仿真與理論值對比圖

采用新的齒型在Ansys軟件中重新進行仿真分析,將新的仿真結果與原仿真值加上補償值之和進行對比,如圖9所示,兩曲線幾乎重合。根據本文理論推導,齒廓的形變主要是由于齒高、齒寬、柔輪形狀以及柔輪材料等因素,雖然微小的齒型修改對于傳動性能以及壽命有較大提升,但是對于齒廓形變來說影響很小。

3.3 齒廓線修正前后諧波減速器性能對比

本文通過修正前后諧波減速器的最大扭矩以及預估壽命兩個關鍵性能指標來衡量對于柔輪齒廓修正的必要性。

(1)對諧波減速器最大扭矩的影響。修正前后的剛、柔輪齒廓線如圖10所示,柔輪輪齒齒頂附近,柔輪齒廓受徑向力影響較大,徑向位移較大,因此實際齒廓線在理論值下方,柔輪與剛輪的側隙增加;柔輪輪齒齒根附近,柔輪輪齒受切向力較大,切向位移較大,因此實際齒廓線在理論值上方,柔輪與剛輪側隙減小。

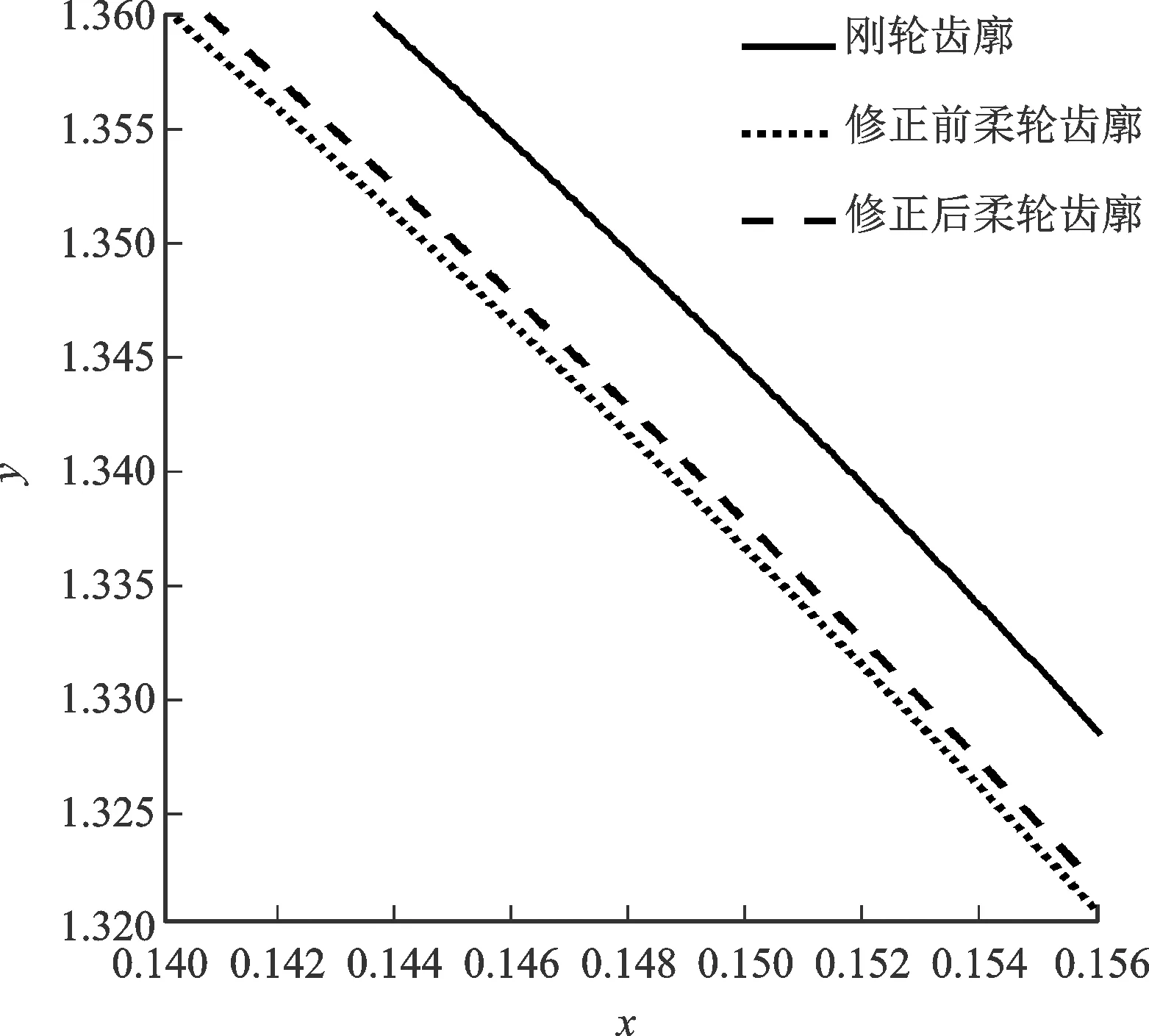
(a)齒頂附近

(b)齒根附近圖10 修正前后剛柔輪齒廓線示意圖

減小初始側隙、增加嚙合齒數,有利于提高諧波傳動的穩定性和承載能力。嚙合齒數通過下式計算

(22)

式中:Φc為剛輪嚙合弧長。

圖11給出了修正前后柔輪齒廓線的側隙大小。臨界側隙嚙合值Im取1.8 μm。可以計算得未修正前嚙合區間為[0°,13.55°],此時嚙合齒數為15.4;修正后嚙合區間為[0°,19.13°],嚙合齒數為21.76。

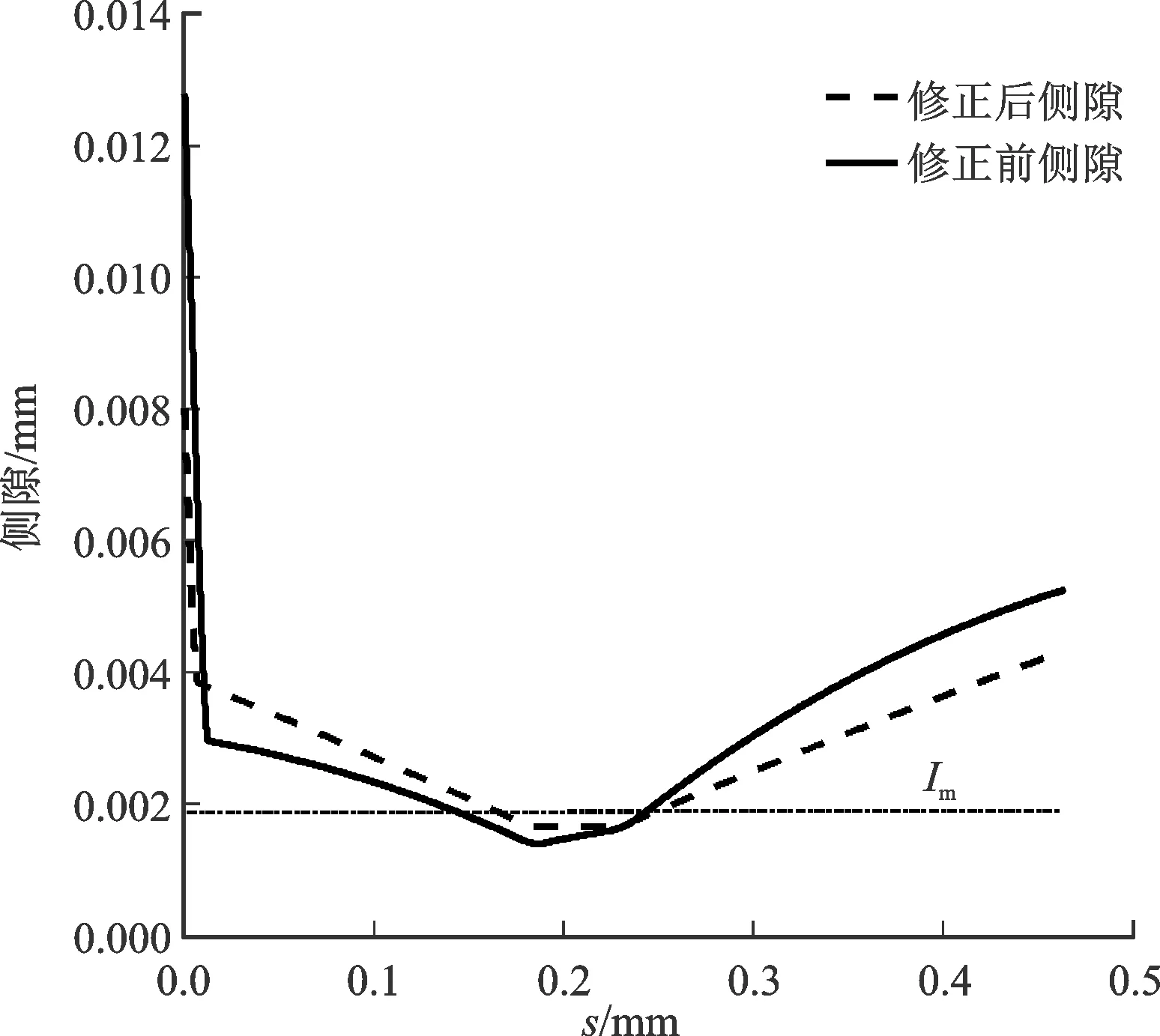
圖11 嚙合初始側隙圖

諧波傳動過程中,受扭矩作用柔輪體彈性形變會使輪齒產生附加位移。一般來說,沿齒廓各點的最小側隙視為該傳動位置的嚙合側隙。如果嚙合側隙過小,則可能導致干涉問題,因此需要對過載扭矩進行限制。

傳動扭矩的近似值由下式給出[5]

(23)

式中:Je為輪齒慣性矩;b為柔輪齒寬;d1為柔輪分度圓直徑;σb為柔輪壁厚;G為柔輪剪切模量。

齒廓線修正前后諧波減速器性能對比見表1。

表1 齒廓線修正前后諧波減速器性能對比

根據表2可知,在滿足側隙要求的前提下,修正后的齒廓能夠承受更大的扭矩,從而提高了諧波傳動系統的承載能力。

(2)對于諧波減速器壽命的影響。諧波減速器可靠性受環境、潤滑等多重因素影響,諧波減速器的預計壽命可以估計為[16]

(24)

式中:TO為輸出軸轉矩;KA為工況系數;T0為許用輸出轉矩,T0=ξTH;NV為轉速。

取傳遞系數ξ=1.5,KA=1.5,NV=1 r/min,TO=500 N·m。計算得到修正前預計壽命L1=3 771 h,修正后預計壽命L2=4 593 h。

4 結 論

本文從柔輪形變的殼體理論出發,計算并分析裝配過程中形變量,得出以下結論:

(1)諧波減速器在實際裝配過程中使柔輪齒型不同部位產生變形差;

(2)以某型號諧波減速器參數為例,采用Ansys軟件進行仿真,同時得到齒型形變的離散數據,采用Matalb軟件對數據進行多項式擬合,計算結果證實了裝配前后齒廓不同位置具有變形差,齒根部分形變大于齒頂部分;

(3)提出了補償方法對原有齒型方程進行優化修正,與原有齒型設計方法進行對比發現,修正后的齒型在嚙合區間增加的同時提高了預計壽命,從而驗證了本文提出的方法。