采用時間序列突變點檢測的滾動軸承性能退化評價方法

劉彈,李曉婉,梁霖,吳杰,徐光華,沈強

(西安交通大學機械工程學院,710049,西安)

隨著機械設備逐漸向大型化、高速化和智能化發展,設備零部件之間的聯系越來越緊密。一旦某零部件失效,就可能導致整臺設備損毀。若能在零部件失效之前定量評價出其性能退化程度,就可以有針對性地進行主動維修,避免惡性事故的發生。因此,開展機械設備零部件性能退化評價對提高生產效益和保障人身安全具有重要意義。

性能退化評價與預測的關鍵在于尋找到與其相適應的特征提取方法、敏感的特征指標和有效的性能退化評價與預測模型[1]。Wang等[2]應用局部線性嵌入(LLE)算法提取高維特征集的低維本征流形特征,利用模糊C均值聚類模型評價軸承當前性能退化狀態。肖婷等[3]利用局部保持投影算法(LPP)對多域高維特征集進行維數約簡,將維數約簡后的特征向量作為最小二乘支持向量機(LSSVM)的輸入,完成退化趨勢預測。Qin等[4]通過局部均值分解(LMD)和主成分分析(PCA)提取特征向量,將其輸入基于分段投票算法和LSSVM的模型中,完成了列車滾動軸承性能退化評價。Gao等[5]將形態腐蝕算子引入數學形態顆粒分析(MMP),提出了廣義數學形態顆粒分析(GMMP),在此基礎上,以GMMP和信息熵為理論基礎,提出了一種基于廣義模式譜熵(GPSE)的退化特征提取方法。Chen等[6]提出了一種基于距離評估技術(DET)的混合域特征提取方法,以提取的退化特征矩陣作為支持向量機(SVM)的輸入,對退化狀態進行識別。Zhao等[7]提出了一種深度特征優化融合方法,從增強型自動編碼器(EAE)處理后的降級特征中選取各模塊的最小量化誤差(MQE)用作候選退化特征,對其進行加權融合以獲得最佳退化軌跡。

以上方法所提取的性能退化特征雖然可以從某個方面反映性能退化過程,但是并沒有形成一個具體有效的評價方法來指導性能退化特征的提取。為此,本文定義了性能退化特征的評價方法,該方法由初始退化點、初始敏感性、失效突變性和趨勢一致性4個指標構成,并設計了性能退化特征評價的定量化指標,且利用時間序列線性突變點檢測的方法給出了評價指標的計算過程,為性能退化特征的選取提供了依據。通過Swiss數據集和滾動軸承加速壽命試驗,驗證了該評價方法和自適應LLE算法的有效性。

1 性能退化特征評價

滾動軸承的性能主要有摩擦、磨損、潤滑和溫升等,表現為滾動軸承摩擦力矩、振動、噪聲和溫度等指標,因此發展出振動信號分析、聲發射信號分析、油液分析、溫度監測、紅外監測、超聲監測、潤滑狀態監測和光纖法等狀態監測方法[8]。振動信號分析是滾動軸承狀態監測方法中使用最廣泛的方法。滾動軸承在表面受損、退化直至失效的過程中,會形成規律性的脈沖激勵信號[9],但信號中的有效信息需經復雜處理方能提取。

振動監測一般是在所關心的關鍵部位布置傳感器,應用數據信號采集卡獲得信號,再利用計算機進行數據計算和分析。常用的傳感器包括加速度傳感器、速度傳感器和位移傳感器,其中后兩種傳感器設計比較冗繁,且增加了制造成本,因此實際使用中多采用壓電式加速度傳感器。

1.1 性能退化曲線

性能退化是通過設備零部件運行狀態的變化表現出來的。性能退化主要表現為4種狀態:正常狀態、初始退化狀態、深度退化狀態、失效狀態。性能退化曲線可以用關于時間t的函數表達,其狀態量是從各個時間點監測信息中提取的特征值,如圖1所示。

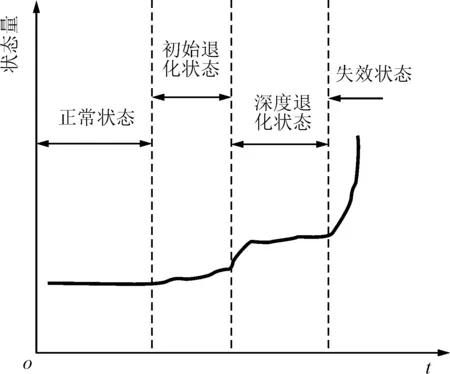
圖1 性能退化曲線

1.2 性能退化特征評價方法及指標

為了有效評價性能退化特征,需要明確性能退化特征的變化趨勢是否在整體上或分階段地保持一致,曲線在變化過程中是否能夠識別退化狀態的起始點和終止點。由此,定義包含4個指標的性能退化特征評價方法。

(1)初始退化點:指性能由正常狀態開始發生背離的時間點,強調發現異常的時間先后。

(2)初始敏感性:指性能從正常到失效狀態過渡過程中初始階段的刻畫能力,此時強調捕捉從正常到異常微小變化的能力。

(3)失效突變性:指性能從正常到失效狀態過渡過程中結束階段的刻畫能力,強調識別異常到失效狀態劇烈變化的能力。

(4)趨勢一致性:指性能從正常到失效狀態整個過程變化趨勢的刻畫能力,強調變化趨勢滿足單一方向變化的能力。

4個評價指標的示意圖如圖2所示。

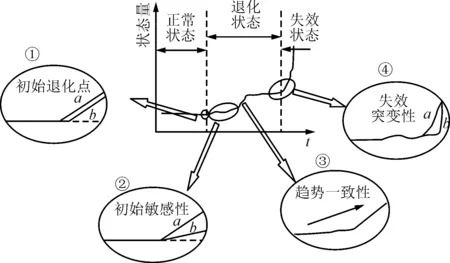
圖2 4個評價指標的示意圖

由圖2可知:階段①曲線a比b更早發生變化,表示a比b對初始退化更加敏感;階段②a比b的變化幅度大,說明a的初始敏感性更好;階段③反映變化趨勢的走向始終保持一致,說明其趨勢一致性較好;階段④a在臨近失效時變化較為緩慢,b則在很短的時間內發生突變,說明b的失效突變性較好。

假設初始退化階段的起始點為t1,終止點為t2,深度退化階段的起始點為t3,失效突變點為t4,失效的終止點為t5,對應的特征值分別為y1、y2、y3、y4、y5。定義性能退化特征評價指標如下。

(1)初始退化點評價指標。性能退化特征開始背離正常狀態的時間點為t1。在樣本數量相同的情況下,初始退化點可以用t1時刻該性能退化特征采集到發生背離的樣本數n1來表示。

(2)初始敏感性評價指標。設備性能開始退化時,性能退化特征曲線不再平穩,而是呈一定的上升或下降趨勢。因此,采用初始退化過程的斜率來表示正常狀態發展趨勢第一次發生變化的明顯程度,即初始敏感性

(1)

式中:y2為初始退化階段終點的特征值;y1為初始退化階段起點的特征值;t2為初始退化階段結束的時間;t1為初始退化階段開始的時間。

(3)失效突變性評價指標。性能由深度退化狀態演變至失效狀態時急劇變化的程度,即為失效突變性。其斜率可能會非常大,甚至趨于無窮,因此不能直接用斜率作為評價指標,而選用斜率的倒數來評價失效突變性

(2)

式中:y5為失效階段終點的特征值;y4為失效突變點的特征值;t5為失效階段結束的時間;t4為失效階段開始的時間。

(4)趨勢一致性評價指標。性能退化特征要求在整體上保持一致或分階段地保持一致。當各階段的斜率符號一致時,說明該性能退化特征曲線的趨勢性在整體上是保持一致的。定義趨勢一致性評價指標

(3)

式中:y3為深度退化階段起點的特征值。

1.3 時間序列線性化突變點檢測

性能退化特征曲線本質上是一個時間序列,各階段起止點在曲線上相當于轉折突變點。要實現性能退化特征指標的計算,首先需要建立特征值與時間點之間的線性回歸方程,然后將變量代入回歸方程中求解回歸系數,通過F檢驗逐步剔除檢驗不通過的變量,最后保留所有顯著變量。

(1)線性回歸方程的建立。時間序列Yt=[y1,y2,y3,…,yn],對應時間點1到n,它們將時間序列劃分成n-1個小區間,在每個小區間內構建一次線性函數

(4)

式中:ai0、ai1(i=1,2,…,n-1)為線性函數的系數。

為便于參數估計,引入線性半截多項式

(5)

式中:r為時間取值區間的節點。

將式(4)轉換成如下形式

(6)

式中:b1、b0、cj(j=1,2,…,n-1)為多項式系數;rj(j=1,2,…,n-1)為時間區間的右端點。

重新設置自變量,令

(7)

則式(6)可以寫成線性回歸形式

(8)

由此便得到了時間序列的線性回歸方程。

(2)顯著變量計算。將性能退化特征值及其對應時間點帶入回歸方程求解回歸系數,然后對所有回歸系數進行F檢驗,并剔除低于顯著性水平閾值Fα的F最小值,直到回歸方程中所有回歸系數對應的F值都大于臨界值。將保留的顯著變量在時間序列上標出,結合性能退化曲線的一般變化規律選擇最合適的狀態變化起止點。該方法的計算過程如圖3所示。

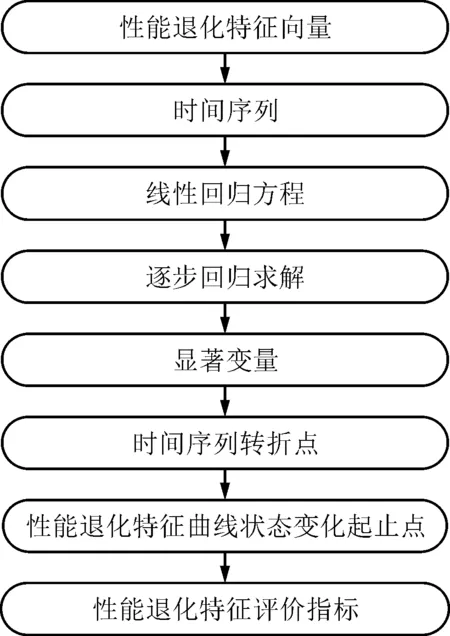
圖3 評價指標計算流程

2 自適應局部線性嵌入算法

2.1 局部線性嵌入(LLE)算法

LLE算法是一種局部非線性降維算法,它假設數據樣本來自一個潛在的流形,每一個樣本與其相鄰樣本所形成的局部區域是線性的。利用鄰域樣本線性重構該樣本以獲取重構權值向量,則該向量中保存了高維數據的局部結構信息。在此基礎上,利用重構權值向量在低維空間嵌入樣本,保證降維前后近鄰樣本之間的結構不變,通過局部線性的疊加,不斷逼近全局的非線性[10]。局部線性嵌入算法的實現可以分為3步,其過程如圖4所示。

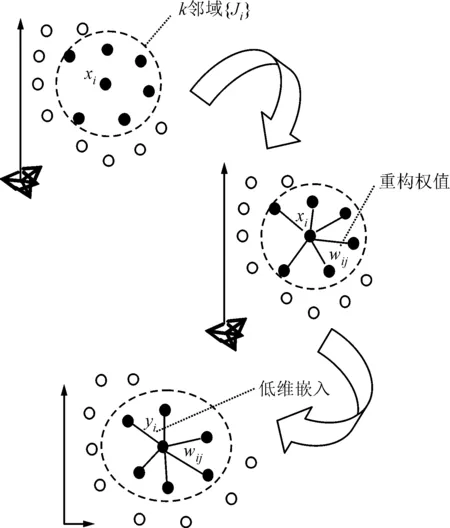
圖4 局部線性嵌入算法實現過程示意圖

2.2 局部線性嵌入(LLE)算法的不足

LLE算法由于參數少,鄰域參數k值的選取對特征提取效果的影響非常大。常規的LLE算法采用全局統一的k值,這對機械信號中大量存在的非線性流形顯然是無法處理的,因為對于非均勻的數據樣本,其周圍樣本的稀疏程度不一致,如圖5所示。

2.3 鄰域參數自適應選取LLE算法

鄰域參數自適應選取的最終目的是保證線性重構得到的重構權向量更準確地反映高維空間中各樣本局部的空間位置關系。合適的鄰域參數能夠使樣本xi與它的鄰域樣本組成一個局部(近似)線性塊。在線性塊內,不僅xi可以由鄰域樣本線性重構,而且線性塊內的其他樣本都可以由剩下的樣本線性重構。采用k+1個樣本的最小重構誤差方差反映各樣本重構誤差的變化大小,方差越小,各樣本重構誤差越接近,k+1個樣本近似位于某個局部線性塊上。退化特征提取方法的實現過程如圖6所示。

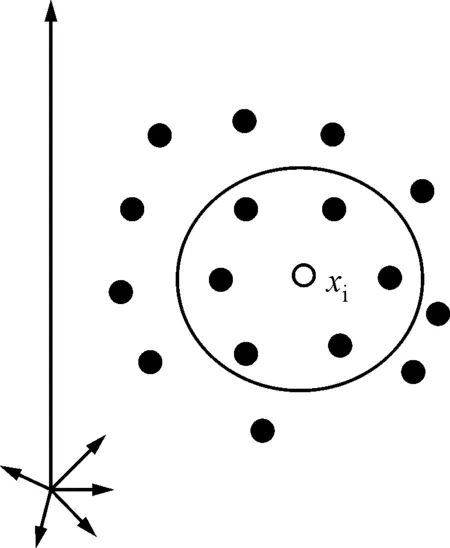
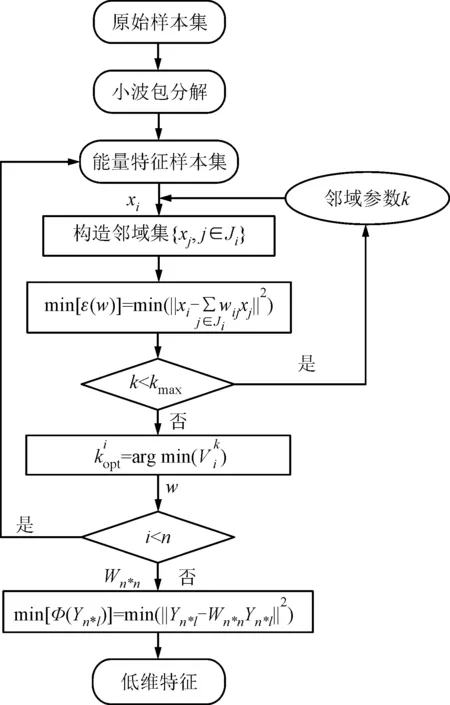
圖6 基于自適應LLE算法特征提取流程圖

基于以上思路,可以確定鄰域參數自適應選取的步驟如下。

步驟1:給定鄰域參數的選取范圍[kmin,kmax](一般k的范圍取2～30),對于樣本xi,?k∈[kmin,kmax],構造xi的k鄰域

Ωi={xi1,xi2,…,xik},i=1,2,…,n

步驟2:?k∈[kmin,kmax],構建樣本塊

步驟3:?k∈[kmin,kmax],計算樣本塊內各樣本的重構誤差

j=0,1,…,k;l=0,1,…,k,l≠j

(9)

步驟4:?k∈[kmin,kmax],計算樣本塊內各樣本的重構誤差方差

(10)

式中

(11)

步驟5:?xi,最優近鄰個數為

(12)

3 實驗驗證

3.1 自適應LLE算法與常規LLE算法的對比實驗

通過比較高維空間和低維空間各樣本距離矩陣的相關性,即平均相關系數,可以反映不同算法的降維效果:平均相關系數越大,則降維效果越好,反之則越差。本文采用流形數據集瑞士卷Swiss進行驗證。Swiss數據集包含2 000個樣本,每個樣本都是三維的,其分布圖如圖7所示。

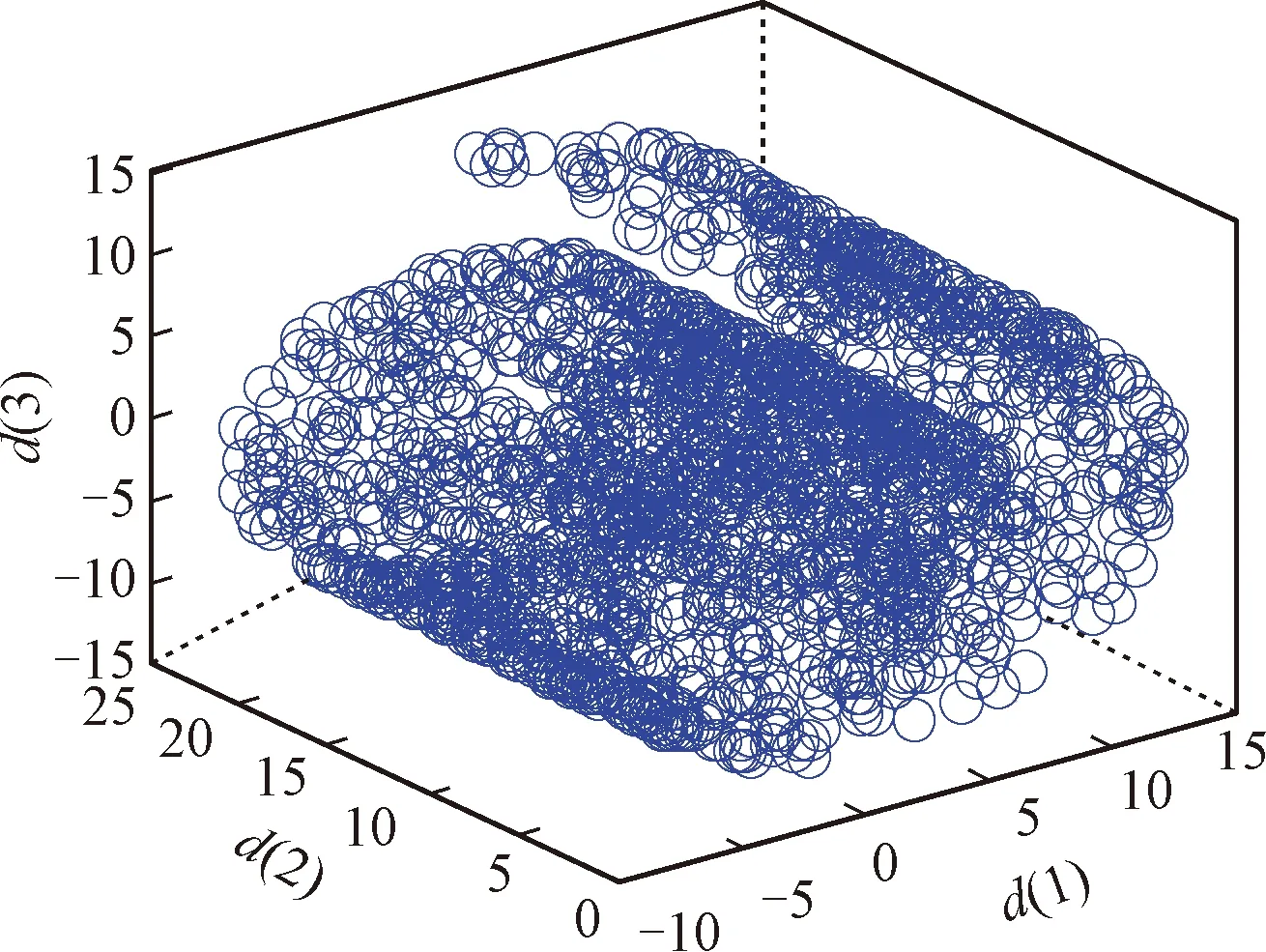
圖7 Swiss數據集樣本分布圖

分別利用鄰域參數自適應LLE算法和常規LLE算法對該數據集進行降維,依次設定k值為5、10、15、20、25、30,低維空間的維數設為2,然后計算各個樣本的平均相關系數,結果如表1所示。

由表1可知,常規LLE算法對于取不同k值的降維效果都較差,平均相關系數都只有0.3左右,而自適應LLE算法其平均相關系數大都在0.7左右,達到了較好的降維效果,由此驗證了鄰域參數自適應策略的可行性。

3.2 自適應LLE降維特征與常規特征評價對比實驗

采用美國智能維護系統(IMS)中心提供的滾動軸承加速試驗數據。軸承試驗裝置結構如圖8所示,輸出軸的轉速大約保持在2 000 r/min。在軸和軸承上,通過彈簧機構施加2 721.55 kg的徑向載荷。潤滑油的溫度和流量參數通過油循環系統進行調節。數據采集所使用的傳感器類型為高靈敏度式加速度傳感器PCB353B33,通過數據采集卡NI-DAQ6062E進行數據采集。在此試驗臺上一共完成3組從正常運行至失效的試驗,以單通道數據采集軸承1發生外圈故障的數據進行驗證。

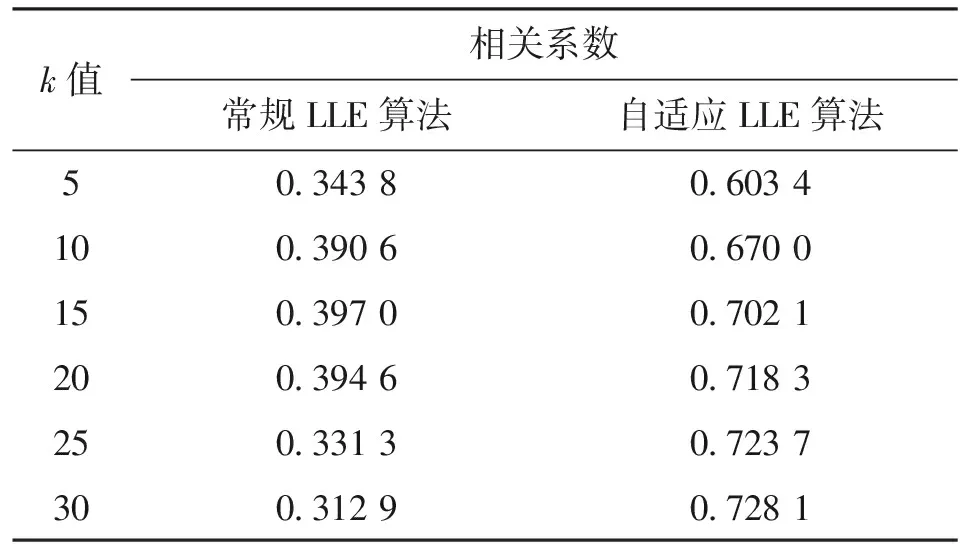
表1 自適應LLE算法與常規LLE算法平均相關系數表

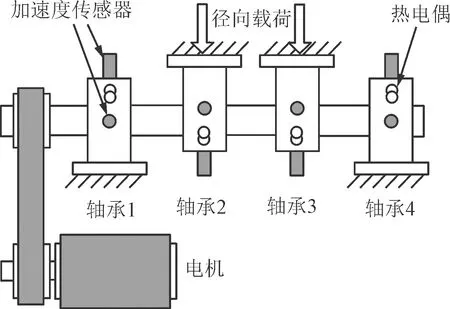
圖8 美國智能維護中心軸承試驗臺結構圖

該組數據共包含984個樣本,每個樣本20 480個點,每次采樣時間間隔10 min,采樣頻率20 kHz,旋轉軸的轉速為2 000 r/min。軸旋轉一周采樣點數為600點。截取原始樣本上連續的4 096個采樣點作為處理樣本,可以得到一個4 096×984的試驗數據樣本集。在此基礎上,首先采用db10小波基對每一個樣本進行三層小波包分解,得到8個頻段的信號,求取每個頻段信號的能量,以8個頻段的能量組成該樣本的特征向量。然后利用自適應鄰域參數選取局部線性嵌入算法進行降維,kmax=20,d=1,其結果如圖9所示。其中橫坐標為樣本數,縱坐標為采用自適應LLE算法降維后的特征值。為了統一評價指標計算的數量級,將降維特征進行等比例歸一化,如圖10所示。

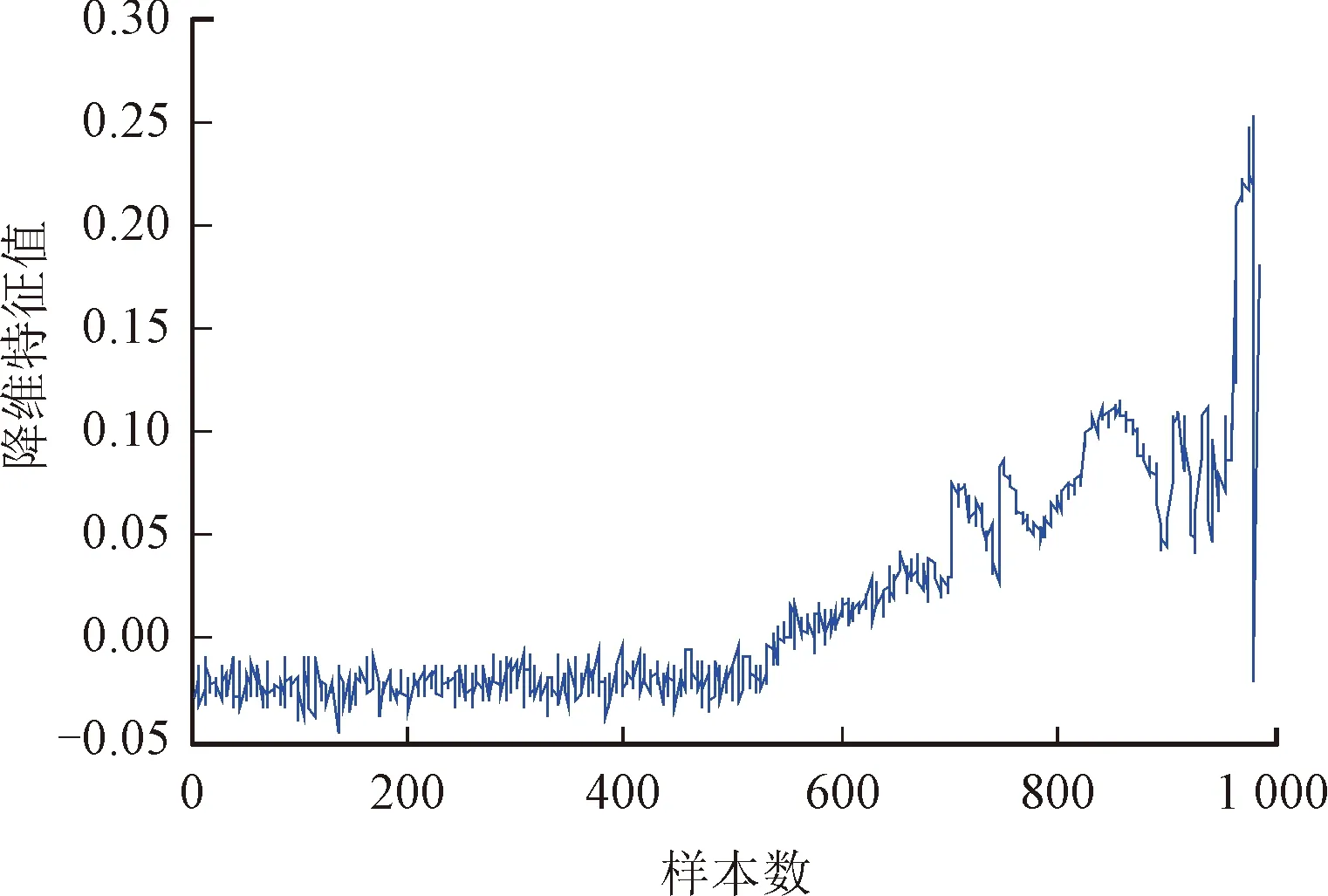
圖9 軸承1降維特征

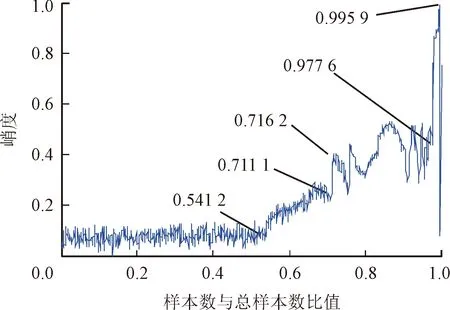
圖10 軸承1降維特征等比例歸一化

為了與降維特征的評價效果進行對比,提取同組數據的均方根和峭度兩個常規特征與之進行比較。等比例歸一化后的峭度和均方根特征分別如圖11和圖12所示。對上述3個特征曲線分別利用時間序列線性化突變點檢測的方法計算各性能退化特征的評價指標,結果如表2所示。

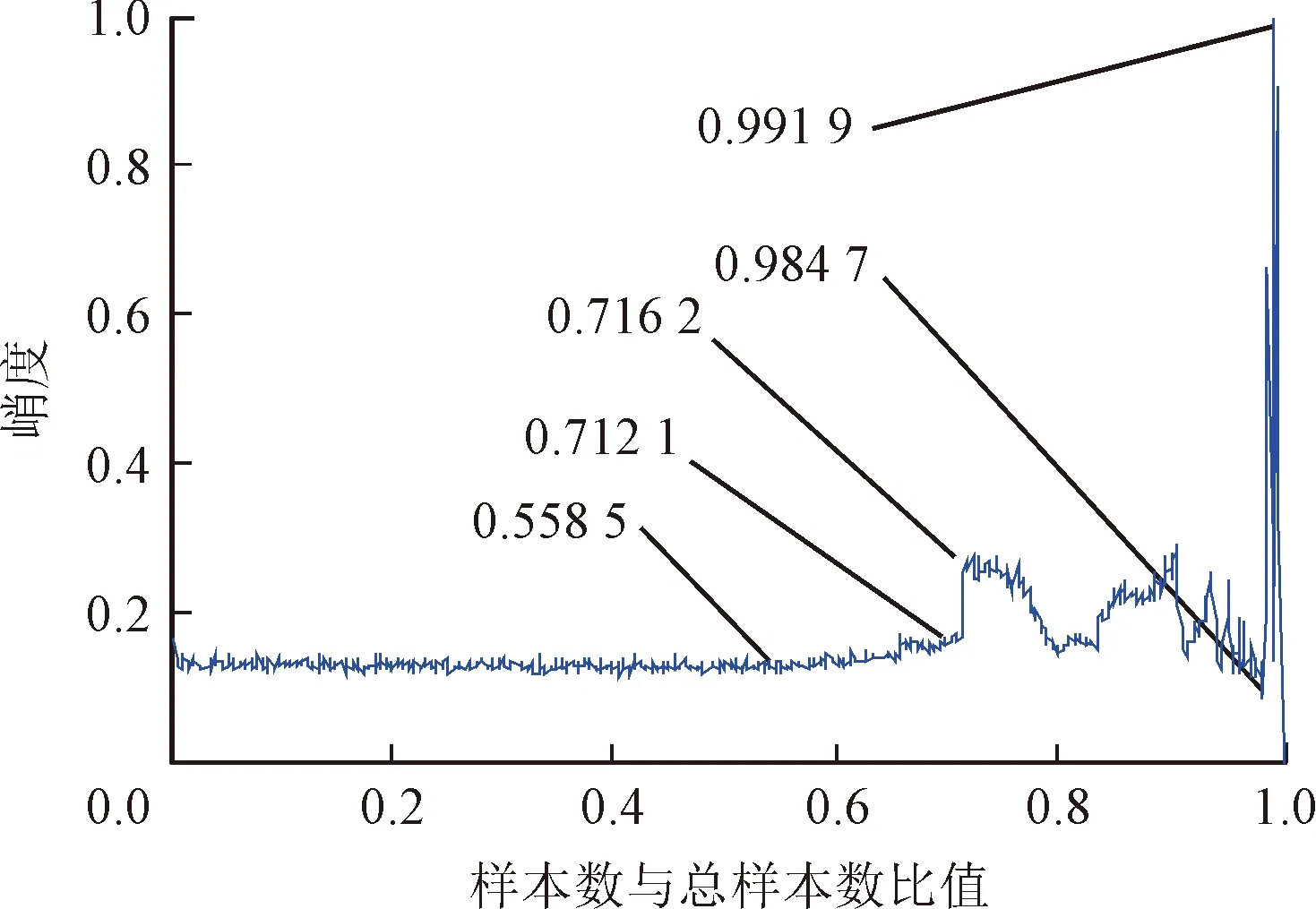
圖11 峭度等比例歸一化

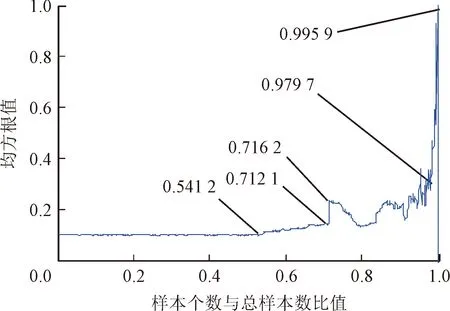
圖12 均方根等比例歸一化

表2 性能退化特征評價對比表

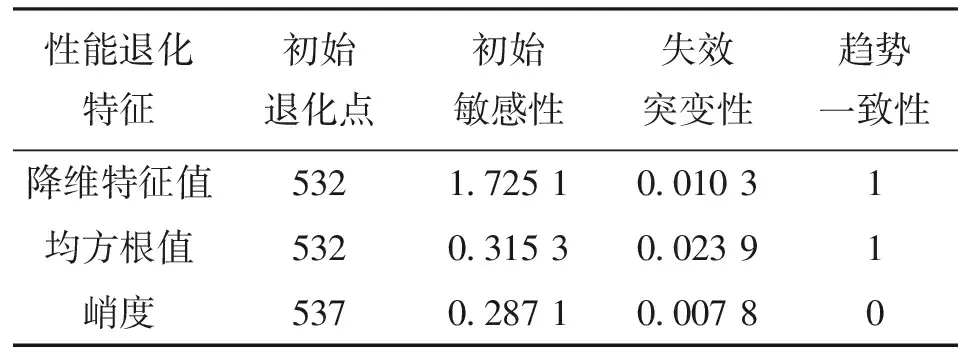
性能退化特征初始退化點初始敏感性失效突變性趨勢一致性降維特征值5321.725 10.010 31均方根值5320.315 30.023 91峭度5370.287 10.007 80

首先,從3個特征曲線上的轉折點可以看出,這些轉折點明顯地將性能退化特征曲線劃分成了4個階段,與實際觀察結果相吻合。其次,由表2中的評價指標可以看出,降維特征和均方根值都比峭度更早地發現初始退化,而且降維特征的初始敏感性比均方根和峭度的初始敏感性大得多;3個特征的失效突變性均趨近于0,對失效突變均有反映;均方根值和降維特征的趨勢一致性指標都為1,而峭度的趨勢一致性指標為0,表明前兩者趨勢一致性較好,而峭度并不具有趨勢一致性。綜合來看,降維特征對性能退化過程的反映能力要優于均方根和峭度,這也與實際觀察結果相符。由此,驗證了性能退化特征提取方法的有效性。

4 結 論

本文主要以滾動軸承為對象,從機械設備零部件性能退化特征評價方法和性能退化特征提取方法兩個方面進行了深入研究,主要得到以下結論:

(1)利用線性函數檢測時間序列轉折突變點的方法可以有效捕捉滾動軸承數據各特征在初始退化、深度退化、失效各階段的起始點和終止點,為性能退化特征的定量化評價提供依據;

(2)性能退化特征評價指標能夠有效地評價滾動軸承性能退化特征的變化過程,為性能退化特征的提取提供依據;

(3)與常規局部線性嵌入算法相比,鄰域參數自適應局部線性嵌入算法更能保持高位空間數據特征的位置關系,達到更好的降維效果。