海拔高程對泄洪霧化影響的敏感分析

柳海濤，徐建榮，孫雙科，彭 育

（1.流域水循環模擬與調控國家重點實驗室，中國水利水電科學研究院，北京 100038）（2.中國電建集團 華東勘測設計研究院有限公司，浙江 杭州 311122）

1 研究背景

大型水電站泄洪霧化對于工程安全與周邊環境有重大影響[1-4]，如何評估與防范霧化危害，是水利水電工程設計中的重要研究課題之一。泄洪霧化的本質是水團、水滴以及水霧在大氣中的運動，其中水舌入水激濺占據主導地位，由此構成了霧化降雨的主體。國內目前主要采用隨機濺水數學模型對霧化降雨進行分析[5-8]，該類模型通過描述每個水滴在空氣中的運動過程，同時考慮空氣阻力、浮力、重力等條件，求得霧化濺水區內下墊面降雨強度分布。上述模型在計算中主要考慮泄洪水力學條件與地形條件的影響，對于海拔高程與氣象條件的影響尚未考慮。

目前我國水電工程建設與運行已從低海拔地區發展到2000 m以上高海拔地區，泄洪霧化與氣象環境之間相互影響不容忽視。從定性的角度看，海拔高程對于霧化降雨的影響，主要體現在三個方面：（1）不同海拔地區大氣壓強不同，從而影響水流摻氣、擴散過程，引起雨霧總量發生改變；（2）不同海拔地區空氣密度與黏滯系數不同，使得霧化水滴在運動中所受阻力、浮力等作用發生改變，引起霧化降雨分布發生改變；（3）不同地域氣壓與空氣密度的差異，使得的泄洪雨霧輸運與沉降過程發生改變，最終影響外圍雨霧濃度分布規律。

針對上述問題，需通過不同海拔地區對比試驗、原型觀測、理論分析、數學模型等手段進行系統研究。鑒于問題的復雜性，本文僅針對海拔高程對于霧化降雨分布的影響，開展探索性研究。通過理論分析，在前人研究的基礎上，建立考慮當地海拔高程影響的泄洪霧化降雨隨機濺水數學模型，結合實際工程霧化原型觀測資料，進行數學模型計算驗證。然后，針對不同海拔高程條件下，泄洪霧化降雨分布的變化規律進行敏感性分析，為今后全面考慮氣象條件對于泄洪霧化過程的影響，奠定理論研究基礎。

2 隨機濺水數學模型的基本理論

將泄洪水舌入水噴射過程視為一種隨機噴射現象，采用拉格朗日方法，對噴射水滴在空氣中的運動進行跟蹤，然后通過統計方法求得濺水區內下墊面上的降雨強度分布。

2.1 水滴運動的微分方程水滴在運動過程中，受到重力、浮力和空氣阻力的共同作用，由此建立水滴運動的力學微分方程：

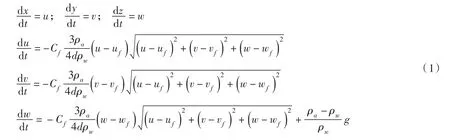
式中：u、v、w為水滴在空間坐標[x、y、z]處的運動速度，m/s；uf、vf、wf分別為水滴鄰近風速，m/s；Cf為阻力系數；d為水滴粒徑，m；ρa為空氣密度，kg/m3；ρw為水的密度，kg/m3；g為重力加速度，m/s2。求解上述方程組需給定水滴初始噴射條件，然后采用4階Runge-Kutta法[9]進行數值求解。

2.2 水滴隨機噴射條件

（1）水滴直徑d采用概率密度函數分布[8]：

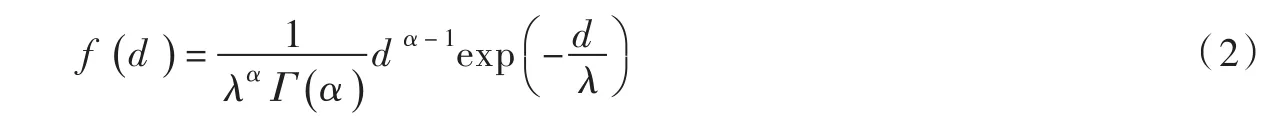
（2）水滴初始噴射速度u采用概率密度函數分布：

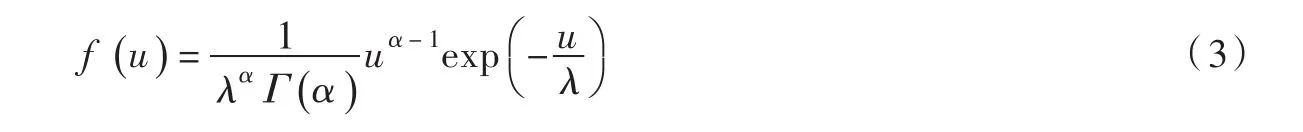
（3）水滴出射角θ采用概率密度函數分布：

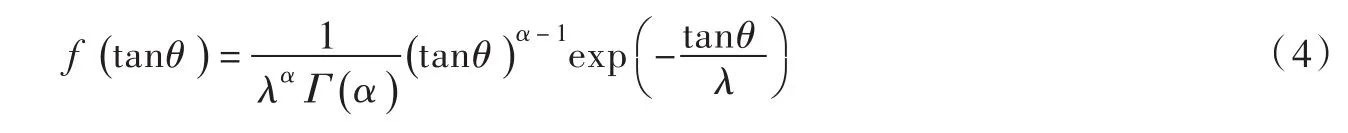
（4）水滴出射偏轉角φ采用概率密度函數分布：

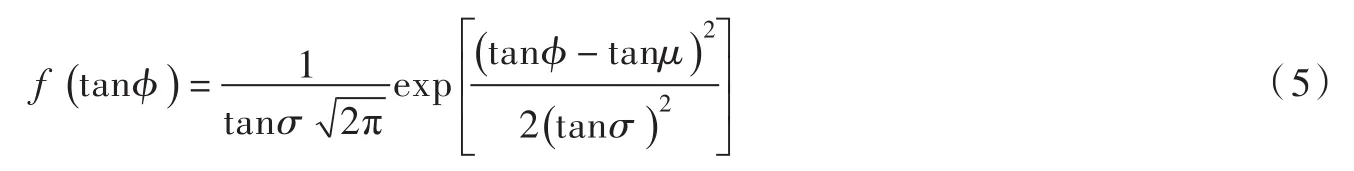
式中：μ為偏轉角眾值，依據水舌平面偏轉角度取值；σ為偏轉角的均方差，σ取值在20°～30°之間，本文取22.5°。

（5）水滴噴射速度與角度的眾值采用下式表示[10]：

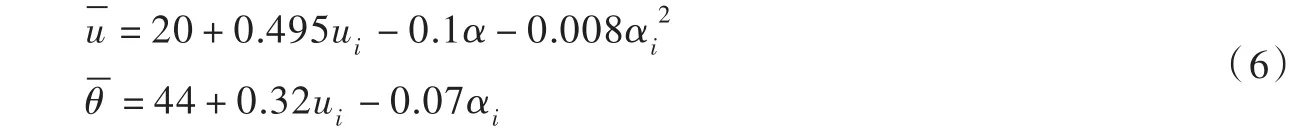
（6）水滴噴射顆粒流量n：

水舌入水激濺主要發生于入水前緣，其噴射厚度h可以表示為[11]：

式中：η為系數，可取25；C為含水濃度，可根據水舌入水時斷面形態判斷，一般地，對于充分發展的摻氣水舌，一般在0.03左右；v為水的運動黏滯系數，m2/s；R為水力半徑，m；u*為摩阻流速，m/s，其表達式為其中τ為空氣阻力

水舌入水噴射的總流量可進一步表示為：

式中：ks為噴濺系數，ks=0.01～0.03，本文取0.01；l為水舌入水前緣總長度，m。

一旦噴射總流量確定，則對應的水滴顆粒流量可以表示為：

式中dm為整個噴射過程的水滴平均粒徑，該粒徑值未知且不同于粒徑眾值。為此，本文模型首先計算粒徑眾值對應的顆粒流量然后，由式（2）中概率密度函數，隨機生成個噴射水滴其對應噴射總流量為最后，式（8）中總流量對應的顆粒流量修正為

通過上式（2）—式（9），可以隨機生成一組噴射水滴，作為初始條件，運用式（1）計算每個水滴的運動過程。

2.3 海拔高程對于水滴運動的影響海拔高程與氣溫的變化，會引起空氣密度、氣壓、黏滯系數、阻力系數的變化，最終引起泄洪霧化降雨分布發生變化。

（1）水滴運動阻力系數 Cf采用下式表示[12]：

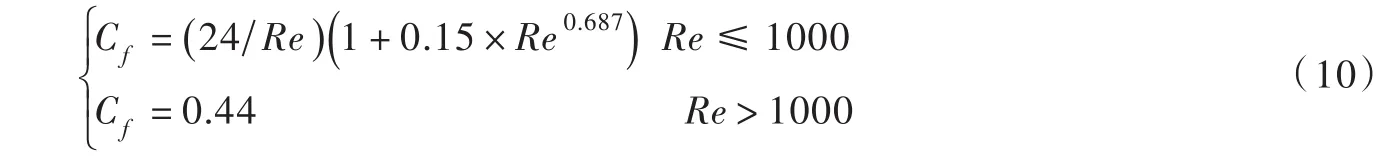
（2）空氣運動黏滯系數 va采用下式表示[13]：

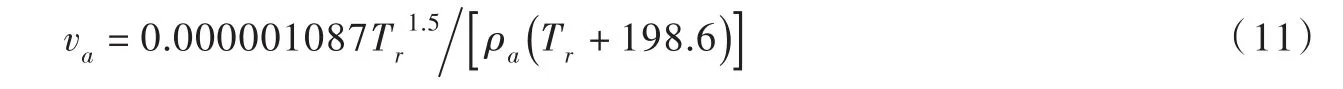
式中Tr為蘭氏溫度，oR，可表示為Tr=1.8Ta+491.67，Ta為空氣溫度，℃。

（3）空氣密度ρa與海拔高程、氣溫的關系可用下式表示：

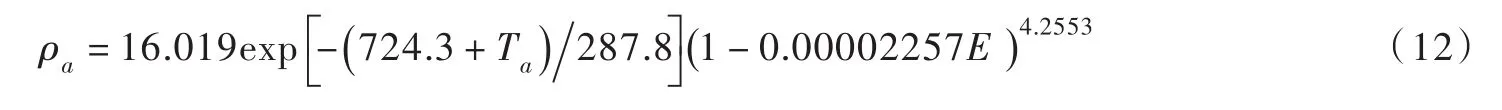
式中E為海拔高程，m。

（4）當地氣壓p與海拔高程E、氣溫Ta的關系采用下式表示：

式中：p0為海平面標準氣壓，取101 325Pa；cp為空氣定壓比熱容，取1005 J/（kg·K）；M為干燥空氣的摩爾質量，取0.02896kg/mol；R0為普適氣體常數，取8.315 J/（mol·K）。

將上式（10）—式（12）與式（1）聯立求解，可以考慮工程當地海拔與氣溫對于霧雨運動過程的影響。由于水舌風與霧化降雨相互伴生，不可分割，以往的研究對于水舌風場多采用正態分布假定或者均一化假定處理。對此，本文通過將三維水舌風場轉換為結構化數據，然后實時求解水滴瞬時鄰近風速，用于閉合式（1）中水滴運動方程，從而較全面考慮河谷中復雜風場對于雨霧運動過程的影響。

2.4 濺水模型的數值計算方法

（1）噴射時間的離散。在濺水過程中，水滴分布于整個空間，只有當水滴到達地面時才能形成降水。為此，在本文模型中，首先，根據水滴自由拋射后在空中的最長停留時間t，確定濺水噴射總歷時T，一般應滿足T≥2t；然后，將計算時間劃分為m個時間步長dt，假設在噴射歷時T內的水滴總量為N=Tn，n為水滴噴射顆粒流量，則每個步長內的水滴總量為Ni=N/m；第三，運用4階龍格-庫塔法求解每個時間步長內水滴的運動方程，其中對于第i個步長內的Ni個水滴，其最長飛行歷時為

（2）降雨強度的計算。降雨強度定義為一定時間內穿過單位面積平面的總水量除以降雨歷時。為此，本文模型中，首先將噴射區域內地面離散為小尺度的集雨網格，然后在每一個時間步長dt內，判斷Ni個水滴的垂向位置，若其在n-1時刻位于地面高程以上，而n時刻位于該平面以下，則表明水滴已降落地面，此時根據其平面坐標，將其水量計入相應的集雨網格，即有Volume=Volume0+πd36，同時該水滴的飛行終止。由于采用隨機函數模擬水滴出射條件，模型需要重復M次噴射過程，當所有M次噴射過程計算完成后，統計平面上每個網格內積累的水滴總體積，再除以噴濺歷時T、網格垂直投影面積A與重復次數M，即可得到該網格內時均降雨強度分布P=Volume/(M AT)。

（3）水滴運動過程中風速與地形的影響。模型求解水滴運動方程中，需要獲取水滴鄰近風速與地面高程，前者用于求解水滴所受風場加速度，后者用于判斷水滴是否降落地面，從而反映兩者對于霧化降雨分布的影響。為此，本文模型中，首先采用相對成熟的Fluent軟件求解三維河谷風場，然后通過相應的轉換程序，將非結構化的三維風場與地形數據轉換為結構化的風場數據Wind(i , j,k)及地形數據[T o po(i , j)]，其中i、j、k為三維結構化坐標，為節省空間，上述數據以二進制文件存儲；隨機濺水模型運行初始，先讀取上述風場與地形數據，并按照其結構化坐標存儲在相應的數組單元中。對于空間任意水滴，若要獲取其鄰近風速，可通過對其瞬時坐標（x,y,z）數值取整，找到其相鄰的8個結構化坐標[Ii,Ji,Ki]，i=1～8。根據其結構化坐標，直接從對應數組單元讀取相應的風速數據，然后插值得到水滴的鄰近風速Ufki為空間插值函數。同樣地，采用二維空間插值方法可以求得水滴的鄰近地面高程。

（4）數值振蕩的抑制。從水滴運動微分方程得知，式（1）中右端項為水滴所受的運動加速度，其阻力項的量值與水滴粒徑成反比，由于采用隨機函數模擬，水滴噴射粒徑為一隨機變量，當某一水滴粒徑趨近于0時，該水滴所受阻力加速度則趨于無窮大，水滴運動則產生數值振蕩。從理論上分析可知，單位時間步長內，水滴所受的最大加速度可表示為UT為水滴終極速度，U0為水滴初始速度，dt為時間步長。在水平方向上，水滴終極速度UT=U0，即為當地風速；在垂線方向上，水滴終極速度為即為重力、浮力、阻力達到平衡時速度。當水滴初始時刻所受的運動加速度為a0≥amax，表明水滴運動速度在該時間步長中已經達到穩態，則在該時間步長中，令a0=amax，下一時間步長中，水滴初始速度U0=UT。

3 數學模型驗證分析

3.1 計算條件中電建昆明院科研所于2014年8月17日，針對小灣水電站泄洪洞全開泄洪過程，水舌入水形態與泄洪霧化進行了原型觀測。觀測過程中，壩上水位1236.32 m，實測泄洪流量3500 m3/s，當地海拔1000 m，氣溫20℃，觀測時間50 min。泄洪洞實地泄洪霧化情況見圖1，水舌入水形成的雨霧在泄洪風場作用下沿兩岸爬升，高度接近300 m，通過沿岸布置霧化降雨測點，得到了下游降雨強度的實測點據。本次觀測工況中泄洪水舌入水條件如表1，水舌入水位置及下游河谷地形見圖2。

圖1 小灣電站泄洪洞全開霧化情況

3.2 水舌風場計算結果泄洪水舌入水過程中，在河谷中形成局部風場，對霧化降雨分布范圍產生影響。根據當地海拔與氣溫條件，由式（11）—式（13）求得當地大氣黏滯系數1.6791×10-5m2/s，大氣密度1.0805 kg/m3，大氣壓強89 999.2 Pa。然后，基于Fluent軟件，求解泄洪洞水舌下游河谷風場。計算中采用了RNGk-ε模型封閉連續與動量方程[14]，水舌入水斷面采用速度邊界，周圍河谷地形按照標準壁面函數進行處理，頂部為壓力出口邊界。圖3為計算得到的河谷地面附近風速等值線圖。由圖可知，河谷泄洪風場受到入水條件與地形的影響，在水舌入水附近風速可達50 m/s量級，然后向外圍逐步衰減，縱向影響范圍可達下游1500 m，兩岸爬升高度超過300 m，其復雜形態對于霧化降雨分布將會產生影響。

3.3 降雨強度分布計算結果根據泄洪水舌入水條件、泄洪風場以及當地氣象參數，采用隨機濺水數學模型進一步計算河谷中霧化降雨分布形態。圖4為泄洪洞下游霧化降雨強度分布形態，由圖可知，霧化降雨分布受到風場與地形的影響，霧化雨區在兩岸爬升高度約250 m，縱向分布范圍受到下游右岸河谷地形的阻擋，邊界位于泄洪洞下游880 m。圖5為泄洪洞下游霧化降雨強度等值線圖，為便于比較，將原型觀測點據一并匯出（圖中方框數據），結果表明兩者在分布規律上甚為吻合。

表1 泄洪洞水舌入水條件

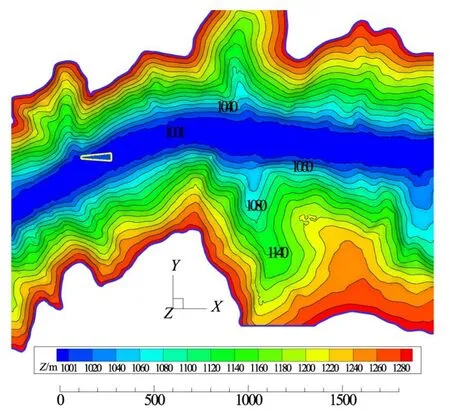
圖2 小灣泄洪洞水舌入水位置與河谷地形等高線

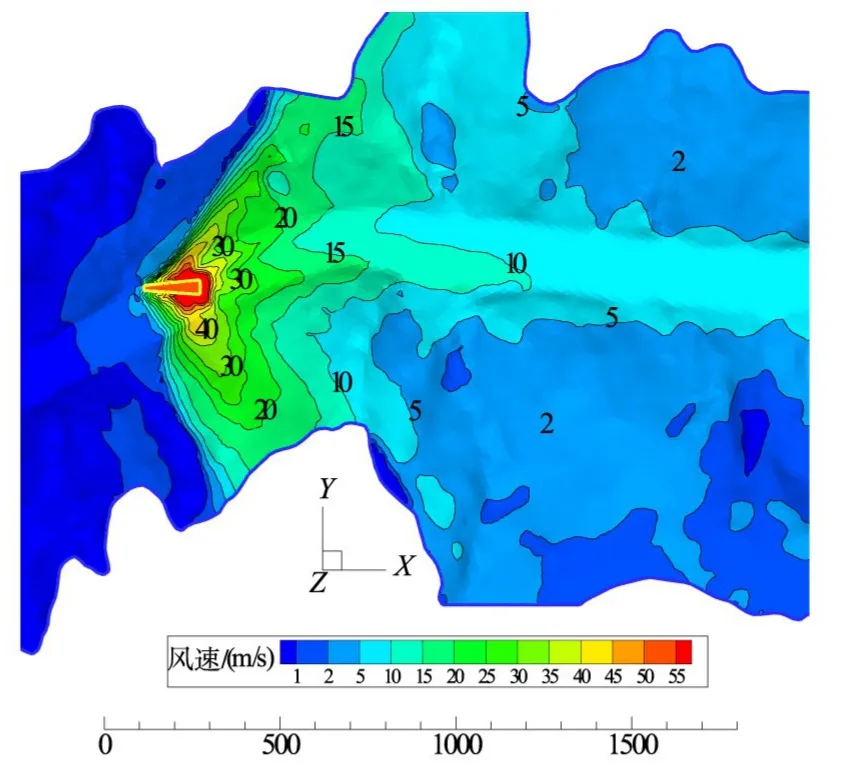
圖3 小灣泄洪洞下游地面附近風速分布

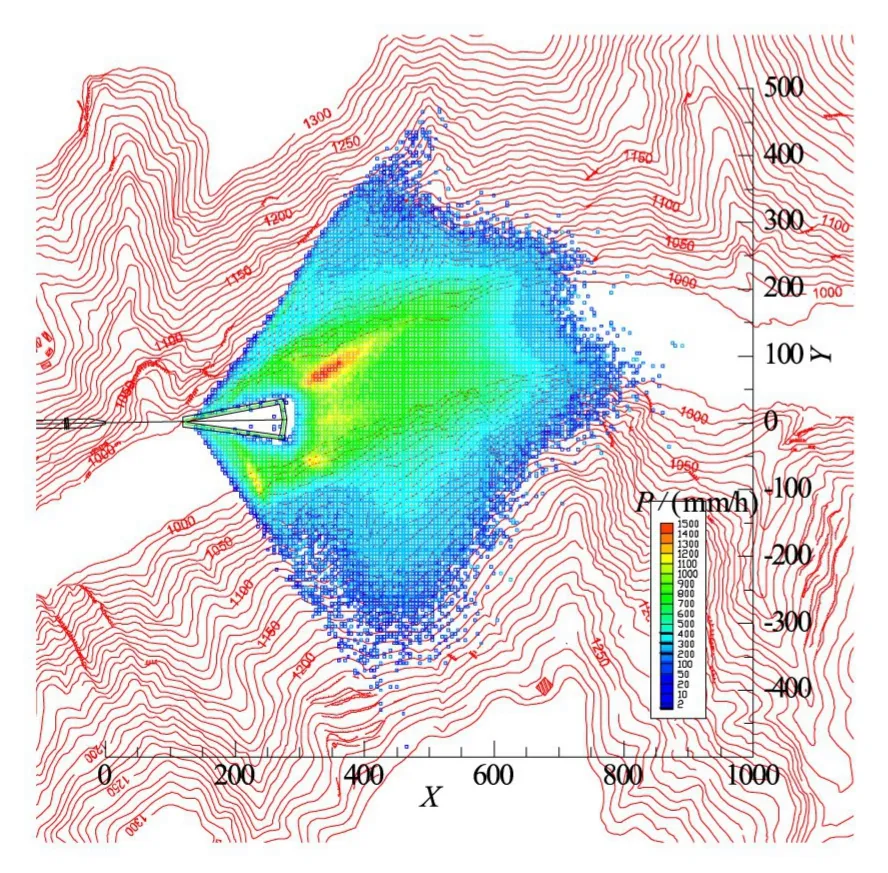
圖4 泄洪洞霧化降雨分布形態

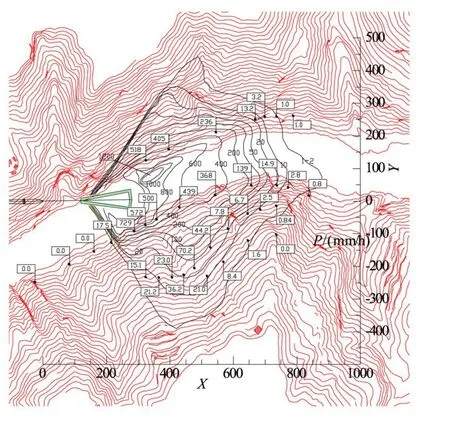
圖5 泄洪洞霧化降雨強度分布

表2 不同海拔地區氣象因子計算結果

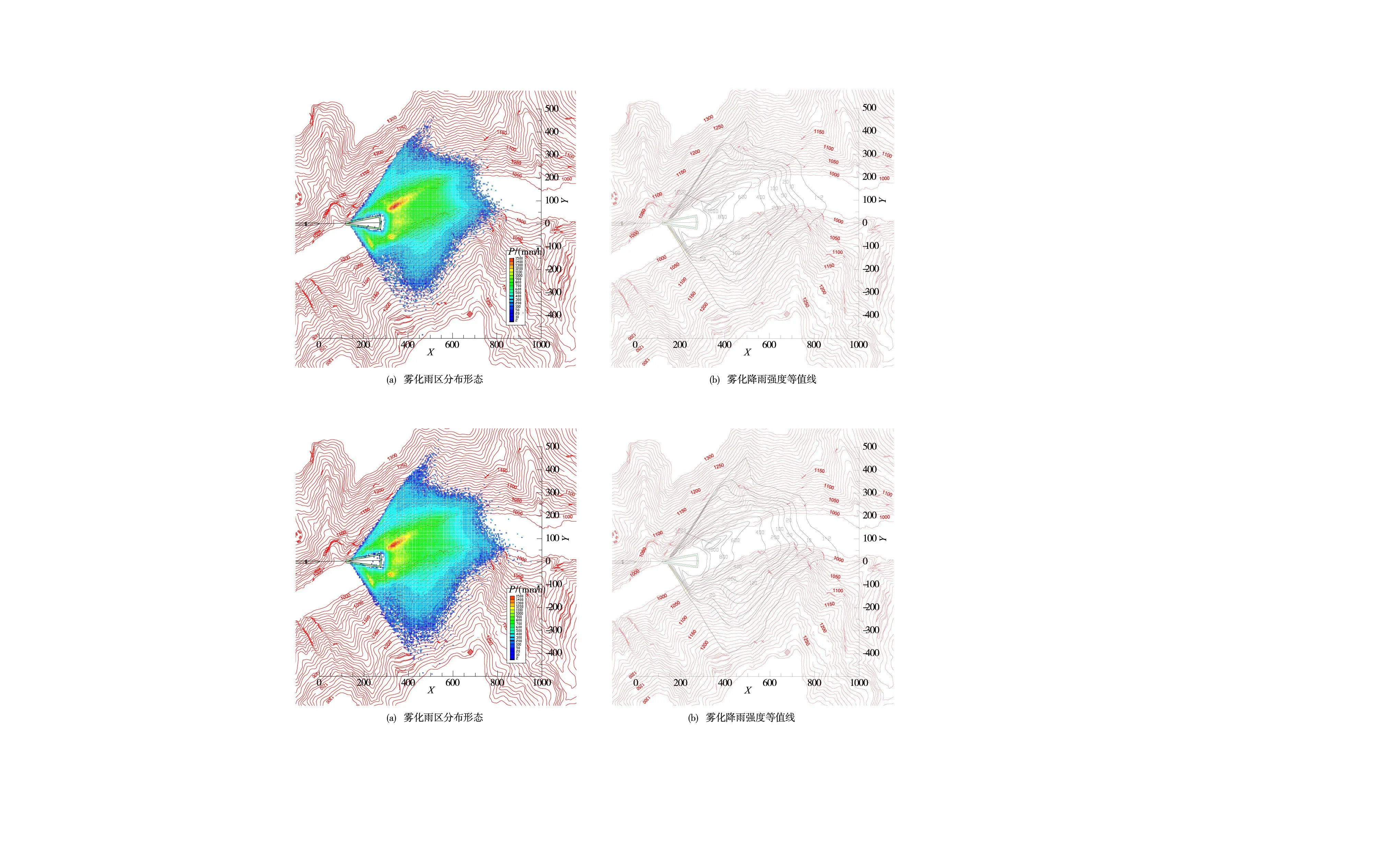
圖6 海拔高程50m條件下泄洪洞下游霧化降雨分布

3.4 海拔高程對于霧化降雨影響的敏感性分析小灣電站當地海拔高程約1000 m，為分析海拔高程的影響，本文在泄洪條件、河谷地形、當地氣溫均不變的前提下，研究不同海拔高程50 m、2000 m、3000 m情況下，泄洪霧化降雨分布的變化規律，上述海拔高程對應的氣象參數見表2。圖6—圖8為不同海拔高程條件下，泄洪霧化降雨分布計算結果，結果分析表明：（1）隨著海拔高程的增加，在相同的泄洪條件下，泄洪洞下游霧化降雨區分布范圍會有所增加。當海拔高程50 m時，兩岸雨區爬升高度約190～220 m，縱向邊界位于泄洪洞下游約850 m；而當地海拔高程3000 m時，兩岸雨區爬升高度可達230～280 m，縱向邊界位于泄洪洞下游950 m，若非受到右岸地形的阻擋，雨區縱向變化范圍會更大。（2）隨著海拔高程的增加，霧化降雨強度分布規律發生坦化。表3為霧化降雨強度沿河谷縱向的分布數據，由表可知，在大于400 mm/h的等值線區域，分布范圍有所減小，而在小于400 mm/h的區域，分布范圍有所增大。（3）海拔高程除了對霧化降雨分布產生影響以外，還會對泄洪雨霧總量以及雨霧輸運過程產生影響，此外氣溫條件也是重要的影響因素，對此需要進一步開展系統研究。

圖7 海拔高程2000m條件下泄洪洞下游霧化降雨分布

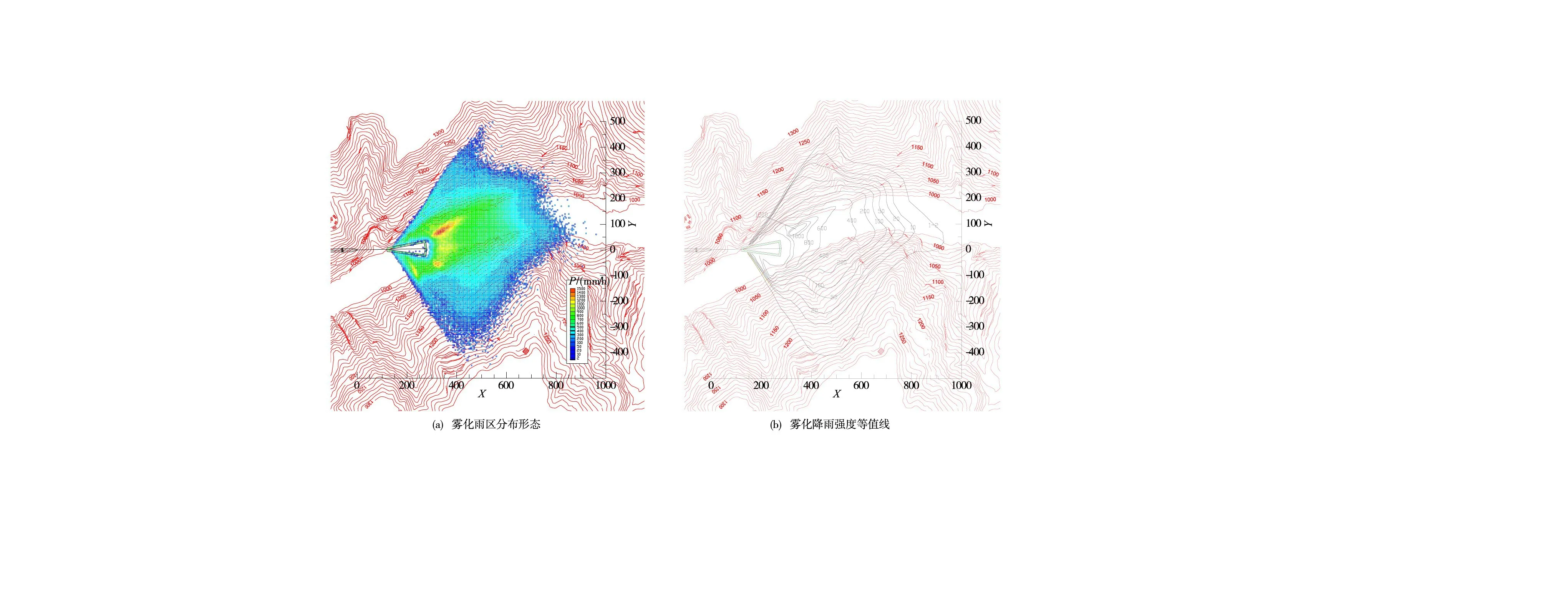
圖8 海拔高程3000m條件下泄洪洞下游霧化降雨分布

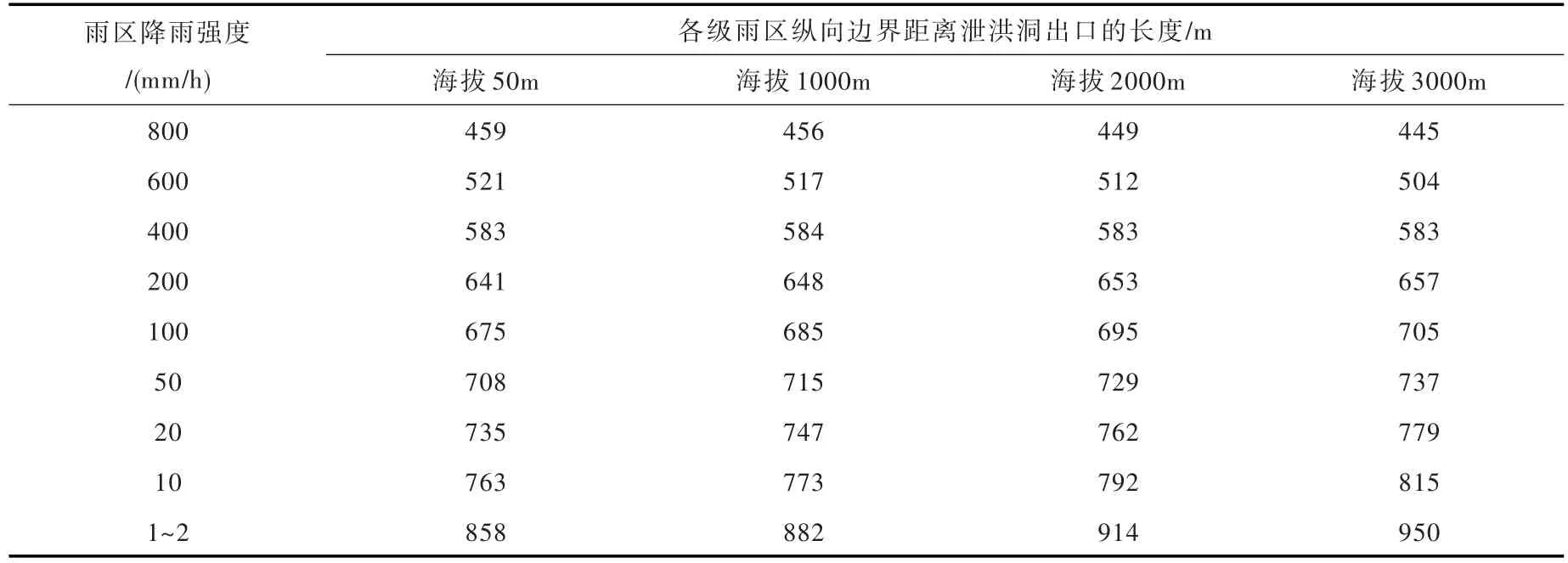
表3 泄洪霧化降雨強度沿河谷縱向的分布數據

4 結語

本文通過理論分析，建立了考慮海拔高程與氣溫條件影響的泄洪霧化隨機濺水數學模型，結合小灣電站泄洪洞霧化原型觀測數據進行了驗證，兩者數據吻合良好。在此基礎上，針對不同海拔高程條件下，泄洪洞下游霧化降雨分布變化規律進行敏感性分析。在泄洪條件、地形、氣溫不變前提下，隨著海拔高程的增加，泄洪洞下游霧化降雨區分布范圍會有所增加，同時霧化降雨強度分布規律發生坦化，證明海拔高程對于霧化降雨強度分布的確存在一定影響。本文研究僅針對泄洪霧化降雨過程，下一步擬對水舌激濺總源量以及雨霧輸運過程，繼續開展海拔高程與氣溫條件的影響分析。