非標(biāo)準(zhǔn)有限差分法求解一類Burgers-Fisher方程

張 艷 敏

(青島理工大學(xué) 琴島學(xué)院, 山東 青島 266106)

擴(kuò)散方程在非線性研究領(lǐng)域占據(jù)非常重要的地位,在生物學(xué)、力學(xué)、物理等領(lǐng)域均有重要作用[1-3].而非線性Burgers-Fisher方程是描述流體動力學(xué)中非常重要的模型之一.很多學(xué)者對這個方程各種性質(zhì)和解進(jìn)行了研究[4-6].比較于線性Burgers-Fisher方程而言,非線性Burgers-Fisher方程更難得到其解析解,或者解析解中含有特殊函數(shù),計(jì)算非常麻煩.所以研究對其進(jìn)行數(shù)值求解是很有必要的.目前常采用的數(shù)值求解方法主要有有限差分法、插值法等方法[7-9].

本文利用非標(biāo)準(zhǔn)有限差分法(NSFD)[10-13]研究非線性Burgers-Fisher方程. 利用NSFD構(gòu)建的非標(biāo)準(zhǔn)有限差分格式比較于傳統(tǒng)有限差分格式具有更好的動力學(xué)行為. 同時給出了差分格式穩(wěn)定性的條件, 并且對數(shù)值解和數(shù)值誤差的特征進(jìn)行分析, 最后通過數(shù)值算例驗(yàn)證方法的有效性.

本文將研究如下非線性Burgers-Fisher方程

ut-ux+uux=uxx+u(1-u).

(1)

其中,u=u(x,t),(x,t)∈(0,L)×(0,T].

初、邊界條件為

式中,L、T為給定的正數(shù),φ(x),φ0(t),φ1(t)為連續(xù)函數(shù).

1 預(yù)備知識

Mickens在文獻(xiàn)[14]中討論了非線性反應(yīng)-對流方程

ut+ux=u(1-u),

給出了一個非標(biāo)準(zhǔn)有限差分格式

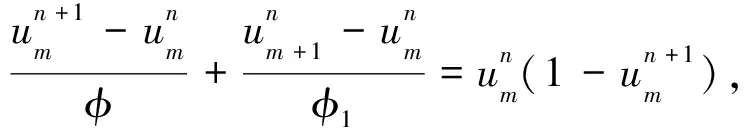
(4)

式中,φ(Δt)=eΔt-1,φ1(h)=eh-1.

式(4)具有如下特征:

1) 取Δt=h,建立了空間步長和時間步長的關(guān)系;

2) 導(dǎo)數(shù)項(xiàng)離散后的分母是關(guān)于步長Δt,h的函數(shù);

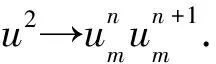
Mickens[15]172-173討論了對流-擴(kuò)散方程

ut+ux=buxx,b>0,

給出了一個非標(biāo)準(zhǔn)有限差分格式

(5)

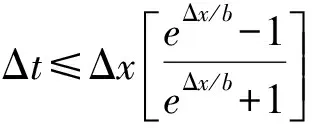
Mickens[15]178-179討論了非線性擴(kuò)散方程

ut=uuxx+λu(1-u),

利用子方程法給出了一個非標(biāo)準(zhǔn)有限差分格式

并討論了式(6)的穩(wěn)定性.

張蕾在文獻(xiàn)[16]中討論了Burgers-Fisher方程

ut+uux=uxx+λu(1-u),

給出了一個非標(biāo)準(zhǔn)有限差分格式

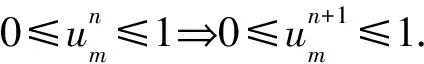
2 非標(biāo)準(zhǔn)有限差分格式構(gòu)造

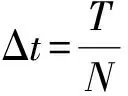
初始條件:

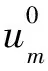
(9)

邊界條件:

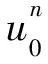
(10)

式中,φ(Δt)=eΔt-1,φ1(h)=2(eh/2-1),φ2(h)=(eh-1),Ψ=sin2h.

式(8)即為式(1)的非標(biāo)準(zhǔn)有限差分格式.

注2 分母函數(shù)φ,φ1,φ2,Ψ均為步長的函數(shù).

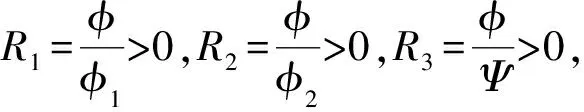
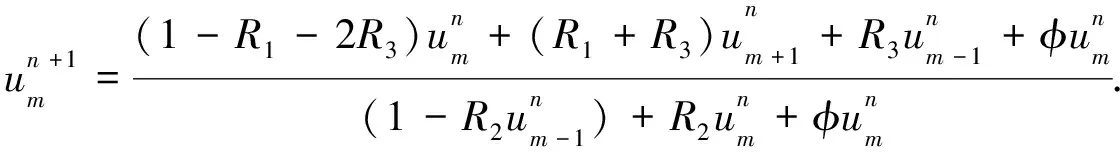
傳統(tǒng)的有限差分格式為

3 差分格式數(shù)值解與數(shù)值誤差的特征

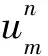
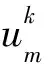
(13)

即滿足

得

R1+R2+2R3≤2,

(14)

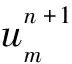
用數(shù)值表達(dá)式(11)的分子減去分母的一部分項(xiàng)得到

當(dāng)

1-R1-R2-2R3≥0?R1+R2+2R3≤1,

(16)

由式(15)、式(16)得

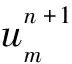
結(jié)合式(14)、式(16)得,當(dāng)R1+R2+2R3≤1時,定理成立.

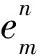
根據(jù)定理1的證明過程,定理2顯然成立.

4 穩(wěn)定性與收斂性的證明

引理1[17](Lax等價定理)給定一個適定的初值問題以及與其相容的差分格式,則差分格式的穩(wěn)定性是收斂性的充分必要條件.

引理2[18-19]差分格式(11)的右端項(xiàng)為非負(fù)時,差分格式是穩(wěn)定的.

定理3 當(dāng)Δt≤ln(1+h(eh-1))時,式(11)穩(wěn)定.

證明 根據(jù)定理1的證明,當(dāng)R1+R2+2R3≤1,即可以保證式(11)右端項(xiàng)均為非負(fù),即

(17)

對式(17)進(jìn)一步整理

穩(wěn)定性得證.

根據(jù)引理2,差分格式也是收斂的.

5 數(shù)值算例

考慮如下定解問題

初始條件:

u(x,0)=e-x,x∈(0,1).

邊界條件:

u(0,t)=et,u(1,t)=et -1,t∈(0,1].

該問題的精確解為u(x,t)=et -x.取h=0.1,Δt≤ln(1+h(eh-1))≤0.010 462.取Δt=0.01,滿足定理1的條件.計(jì)算數(shù)值解的相對誤差見表1.

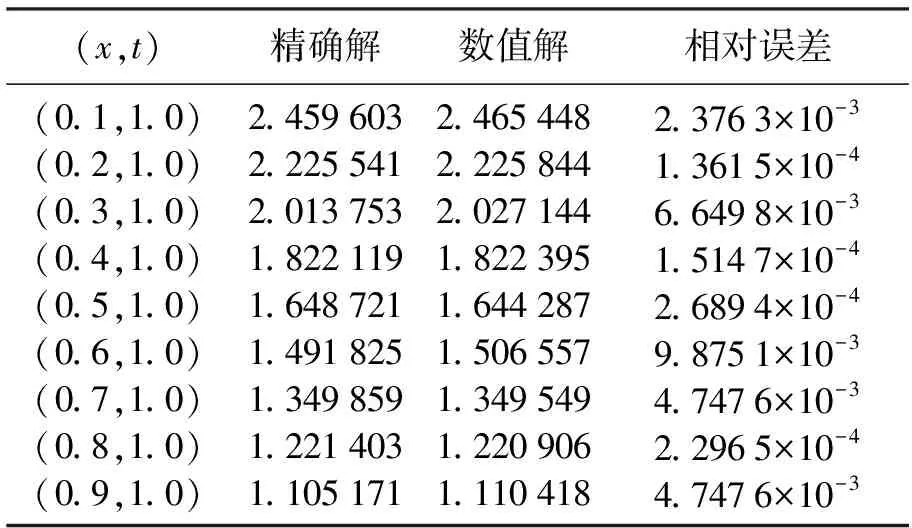
表1 數(shù)值解相對誤差Table 1 The relative error of numerical solutions

利用傳統(tǒng)的有限差分格式(12)對上述算例使用與式(11)相同的時間和空間步長進(jìn)行計(jì)算.當(dāng)計(jì)算到第16層,即n=16時,數(shù)值解就達(dá)到了1043數(shù)量級,說明數(shù)值計(jì)算格式(12)是不收斂的.即非標(biāo)準(zhǔn)有限差分格式(11)對時間和空間步長的使用條件更廣泛,穩(wěn)定性與收斂性更好.

從表1可以看出,利用非標(biāo)準(zhǔn)有限差分法求解此類方程精度較高,差分格式數(shù)值解和數(shù)值誤差具有很好的適定性,因此該方法在求解此類方程時是一個有效的方法.

6 結(jié) 論

1) 對于非線性項(xiàng),利用非局部離散方式可以保持差分格式的收斂性與穩(wěn)定性.

2) 導(dǎo)數(shù)項(xiàng)離散后的分母利用步長函數(shù)進(jìn)行逼近可以提高數(shù)值精度.

3) 非標(biāo)準(zhǔn)差分格式數(shù)值解與原微分方程解析解可以保持相同的動力學(xué)行為.