基于Gauss偽譜法的火箭空間投送軌道設計*

魏鵬濤，龍霞

(火箭軍指揮學院，湖北 武漢 430012)

0 引言

在現代戰爭中，防御方為了提升戰場生存能力，大量采用隱身技術、修筑堅固掩體，給進攻方進攻作戰帶來了巨大的挑戰，成為擺在其面前的一道難題。如何有效破解這一難題，各國競相展開了相關研究，這些研究大部分集中在武器裝備、情報偵察、戰術戰法等方面，對目標的攻擊方式還僅局限于傳統的陸地、海上及空中，因而戰時對堅固掩體目標實施有效摧毀的可能性較低。為了顯著提高打擊效能，充分發揮空間優勢，本文提出利用火箭將打擊載荷或二次平臺投送到太空，從太空實施自上而下的搜索和追蹤的攻擊方式[1]。如何實現火箭的快速投送，投送軌道的優化設計異常重要。對于火箭投送軌道的優化設計，目前有多種方法，其中偽譜法是一種行之有效的方法，其主要原理是基于插值多項式對優化軌道進行直接配點，能用較少的節點來獲得較高的精度[2-7]，因而該方法既降低了計算的復雜性，同時又保證了算法的實時性。相比于其他偽譜法，Gauss偽譜法計算效率更高、準確性更好、魯棒性更優[8-10]。因此，本文選用Gauss偽譜法對火箭投送軌道進行優化設計，本文方法可為火箭空間快速投送方式實際運用提供借鑒和參考。

1 Gauss偽譜法軌道優化原理

對于火箭空間軌道快速投送優化問題，其實質是進行火箭投送的最優控制，因此可將該問題最終歸結為最優控制問題。而對于最優控制問題而言，狀態變量和控制變量是其基本的2個要素，Gauss偽譜法是將這2個要素在一系列高斯點上進行離散處理，并在這些離散點上通過構造Lagrange插值多項式來逼近狀態變量和控制變量這2個要素，緊接著對插值多項式進行求導用來近似狀態變量求導，從而用一組代數約束替代與軌跡相關的微分方程約束[11]。

(1) 最優控制問題

對于火箭快速投送軌道優化問題，可以采取多種處理方式，其中最有效的處理方式是將其描述為最優控制問題。要解決最優控制問題，則需要搜索獲得最優控制變量u(t)(u(t)∈Rm)，其需要滿足的性能指標可表述為

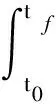
(1)

在式(1)中，對于狀態變量x(t)(x(t)∈Rn)而言，t0為火箭投送初始時間，tf為火箭投送終端時間，狀態變量x(t)需要滿足以下動力學微分方程約束：

(2)

其中:狀態變量x(t)的邊界條件約束為

φ(x(t0),t0,x(tf),tf)=0,

(3)

狀態變量x(t)的路徑條件約束為

C(x(t),u(t),t)≤0.

(4)

(2) 多階段不連續最優控制問題

從以上的處理方式可以得出：對于火箭快速投送軌道而言，其上升段優化問題可歸結為多階段不連續最優控制問題。對于該問題，在具體處理時可將不同飛行段之間的斷點設置為連接點，同時將火箭投送飛行的時間區間進行分段，然后分別對每一段進行不同配點，最后再結合相應約束條件進行處置。假設所設置的某一斷點τ1(τ1∈[τ0,τ2])不連續，則可以表述為

(5)

τ1點的約束條件為

φx(x-(τ1),x+(τ1))≤0，

(6)

當τ1點的值不確定時，還需要補充以下約束條件

τ1-τ2≤0.

(7)

(3) 邊界控制變量計算

Gauss偽譜法是在LG點上所進行的離散處理，但該處理方式并不包括邊界點的值。因此，對于Gauss偽譜法而言，其不能求得優化問題起始邊界處控制變量的值。但是在火箭快速投送軌道優化問題的求解中，邊界控制變量卻顯得尤為重要。目前，對于邊界控制變量值的求取，基本的方法是由配點處的值進行外推來得到，但該方法求解得出的值很可能不是最優解，從而導致最優控制問題不能得到最終解決。因此，為了解決這一問題，本文采用以下方法進行求解：

對于Hamilton函數

H=g+λTf-μTC.

(8)

依據極小值原理，可以讓最優控制變量u*(u*∈U，U為控制變量的可行域)滿足以下條件

H(x*,u*,λ*,μ*)≤H(x*,u,λ*,μ*).

(9)

假設x*(τ)，λ*(τ)和μ*已知時，μ*(τ)的求取可以歸結為一個有約束的優化問題。此時，可以采用Hamilton函數的另外一種表達形式(不含路徑約束)

(10)

對于式(10)的表述方式，可將路徑約束最終納入控制變量組成的集合,則

U0=U∩C0，

(11)

式中:U為τ0時刻控制變量u*的所有可行解;C0為τ0時刻滿足路徑約束的控制變量u*的集合。因此，u*(τ0)的求解便轉換為對下述問題的求解

(12)

2 火箭投送軌道Gauss偽譜法優化模型

2.1 火箭投送軌道上升段動力學模型

本文研究的火箭為三級固體火箭，該火箭采用三級固體發動機和液體末助推的串聯式結構布局，其整個飛行過程可分為：一級、二級、三級動力飛行段以及末助推段。為了簡化對問題的描述，此處假設地球為圓球體，選擇地心赤道坐標系作為參考坐標系，在該坐標系下建立火箭空間投送的動力學方程為[12-14]

(13)

式中:μ=GM為地球引力常量；T為投送火箭的發動機推力；Isp為投送火箭的發動機比沖；r(t)=(rx,ry,rz)T為投送火箭的位置矢量；v(t)=(vx,vy,vz)T為投送火箭的速度矢量；u=(ux,uy,uz)T為投送火箭發動機的推力方向；氣動阻力D=(Dx,Dy,Dz)T可表述為

(14)

式中:CD為阻力系數;Arel為投送火箭的參考面積;ρ為大氣密度;vrel為相對運動速度。其中ρ的計算式為

ρ=ρ0e-h/h0,

(15)

式中:ρ0=1.225 kg/m3；h0=7 110 m。

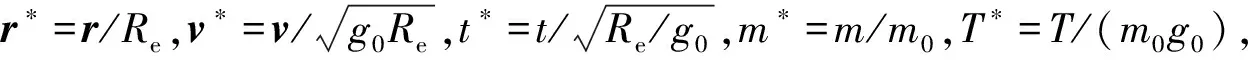
(16)

2.2 約束條件

對于邊界約束條件。對火箭直接上升投送軌道而言，火箭的初始位置已知，只是發射時刻未定，因此將終端約束定為xf，yf，zf，當優化時間tf，獲得時，則可確定發射時刻。

對于路徑約束條件。其中，火箭飛行的高度約束為

|r|≥Re.

(17)

火箭推力方向約束為

|u|=1.

(18)

火箭動壓約束為

(19)

火箭視加速度約束為

(20)

對于連接點約束條件。火箭投送軌道的4個飛行段通過3個連接點連接，這3個連接點處的約束為

(21)

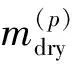
2.3 目標函數

本文研究的固體火箭在飛行過程中，前三級發動機均采用耗盡關機工作模式。因此，火箭投送軌道優化問題的目標函數可選取為末段助推消耗液體推進劑質量最小，即末助推級工作結束后的火箭剩余質量最大，目標函數具體可以表述為

J=-m(4)(tf).

(22)

2.4 軌跡快速優化策略

應用Gauss偽譜法求解過程中，離散點的選取對設計變量的影響非常大，當離散點數量過多時，計算量將大大增加，而且Gauss偽譜法計算效率高的優點不能充分體現，甚至由于選擇初值不恰當而使優化問題收斂到不可行解，這樣最優化問題無法得到解決，火箭快速投送最優化軌道便陷入死結。為了解決這一問題，經過多次探索實踐，最終形成了比較好的解決方案，在此本文提出策略為：首先構造設計變量的初值生成器，隨后在各飛行段通過采用較少的節點來計算近似的最優軌跡和控制變量，再以此作為下一步利用較多節點進行計算的初值。此策略不僅可以較好解決初值選擇不恰當而得不到可行解的問題，而且可以有效發揮Gauss偽譜法計算效率高的特點。

2.5 仿真優化與結果分析

假設本文采用的用于空間投送的火箭發動機參數如表1所示，其中，液體末助推級干重為200 kg，推進劑質量為250 kg，比沖為300 s，推力為2 000 N。該型火箭空間投送的有效載荷為400 kg，投送火箭整流罩的質量為200 kg。

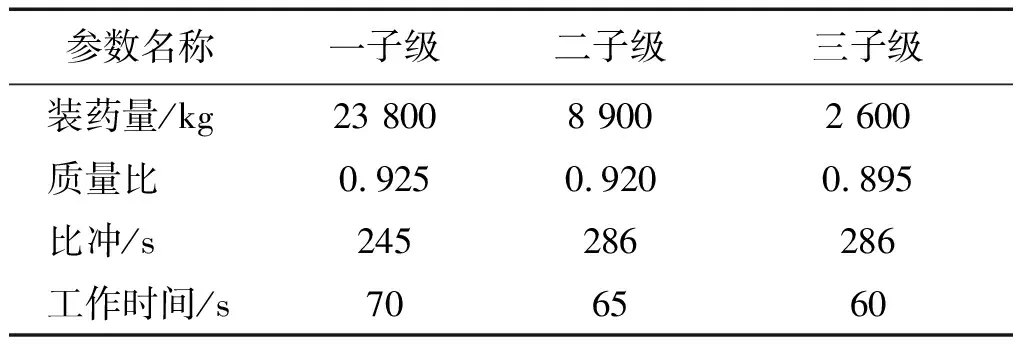
表1 投送火箭發動機性能參數Table 1 Performance parameters of rocket engines

假設火箭初始位置為r0=(2 196 550.3，-4 773 009.7,3 615 829.6)m，火箭投送終點位置為rf=(3 058 828.4,-3 883 092.5,4 532 124.3)m。選擇地心直角坐標系為參考坐標系，在地心直角坐標系下，火箭初始和終點位置均為該坐標系下的坐標。

本文優化選擇的仿真條件為：CPU為920/2.67 GHz，內存為4 G，操作系統為Windows 7，編譯環境為Matlab 7.1[15]。軌跡快速優化策略采用Gauss偽譜法初值生成器優化策略。在生成計算初值時，將火箭投送多個飛行段LG點的數量設定為5，在進行精確計算時，將火箭投送多個飛行段LG點的數量設定為15。

假定2019-06-01T19：46：40為火箭投送空間目標終點位置時刻。根據火箭投送軌道運行的星下點軌跡，可將投送火箭發射點的天文經度設定為106.394°，可將投送火箭的發射點天文緯度設定為37.715°。通過發射點的天文經緯度坐標以及目標投送點位置坐標，因而可求得發射點的瞄準方位角為169.081°。通過仿真計算，火箭投送全程的飛行時間為280 s，因此，投送火箭發射時刻應設定為2019-06-01T19：42：00。具體仿真結果如圖1～5所示。

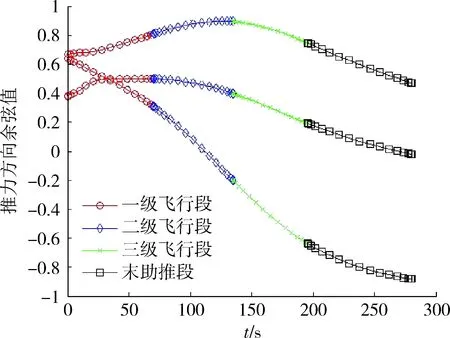
圖1 推力方向變化曲線Fig.1 Thrust direction change curve

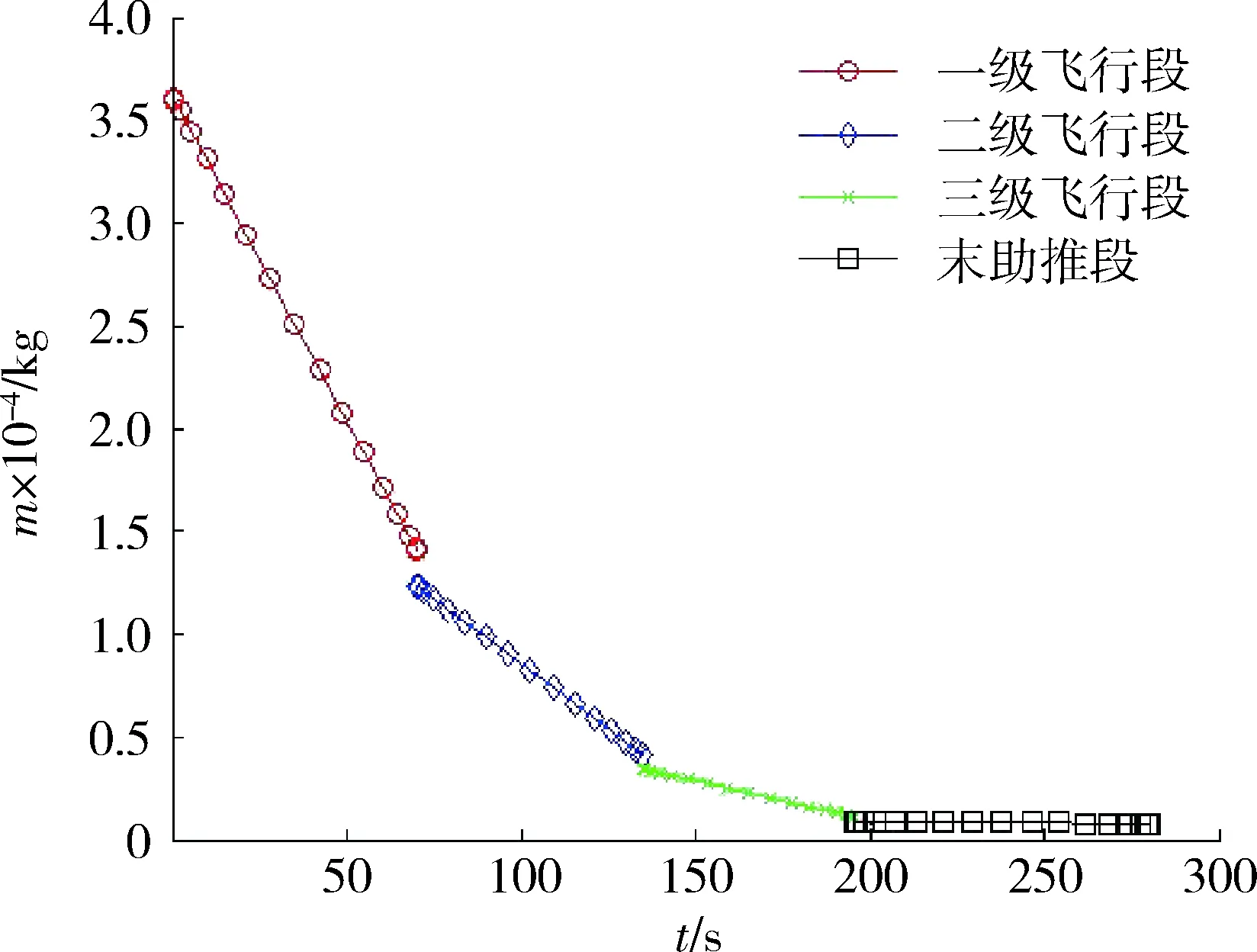
圖2 質量變化曲線Fig.2 Mass change curve

將通過Gauss偽譜法進行仿真計算得到的最優軌跡數值與通過數值仿真計算得到的軌跡數值進行對比分析，可以得到上述2種方法對于投送終端位置的計算誤差分別為：Δx=1.563 m，Δy=0.273 m,Δz=0.421 m。從2種方法的計算誤差可以看出，采用Gauss偽譜法進行火箭投送軌道優化計算具有較高的求解精度。其中，從仿真圖1可以看出，控制變量對于投送火箭推力方向變化比較平緩，此結果表明在火箭各級分離點處，各飛行段前一階段末端控制變量與后一階段初始控制量之間的誤差很小，從而證明了采用的邊界控制變量值這一計算方法計算精度比較高。從整個仿真來看，火箭投送軌道優化所用總時間為113.4 s，其中，初值生成時間為65.1 s，精確計算時間為48.3 s。傳統優化算法，用時約為420 s左右，相對于傳統優化算法，Gauss偽譜法計算效率較高，優勢明顯。通過上述仿真計算結果可以看出，Gauss偽譜法可以用于火箭空間快速投送軌道優化，并且具有獨特的優勢。

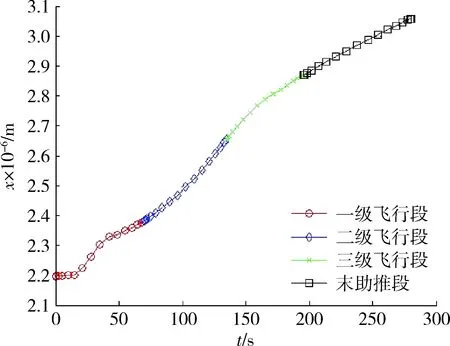
圖3 x軸位置變化曲線Fig.3 x-axis position change curve

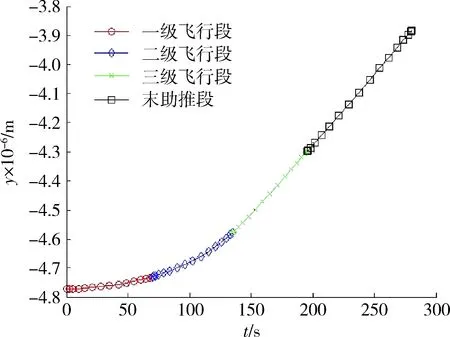
圖4 y軸位置變化曲線Fig.4 y-axis position change curve

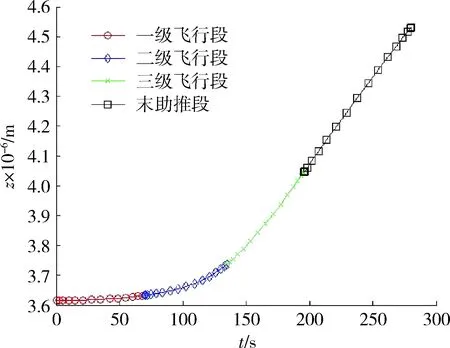
圖5 z軸位置變化曲線Fig.5 z-axis position change curve

3 結束語

利用火箭投送距離遠、運動位勢高的特點，將打擊載荷或二次平臺投送到空間，從太空發起進攻成為未來戰爭的一種重要作戰方式。本文針對火箭空間快速投送軌道優化問題，利用Gauss偽譜法計算效率高、準確性好、魯棒性優的特點，建立了優化模型并進行了仿真計算，結果表明該方法的可行性。本文的研究是將地球假設為圓球體，相應的模型建立與實際還有不小的差距，所得出的結果只是對方法的可行性進行了論證，下一步，將建立精確的地球軌道模型進行精確求解，從而為火箭空間快速投送實際應用提供理論借鑒和參考。