勾股定理和方程更配哦

柏黎平

同學們都知道勾股定理的重要性，它可以用等式a2+b2=c2（其中a、b是直角邊，c是斜邊）表示直角三角形三邊關系。方程思想是初中數學解題的重要思想方法，它利用等式作為數學思維工具解決問題，化未知為已知。勾股定理等式中如果存在未知數，那么它就具備了方程的特性。因此我們在利用勾股定理計算邊長時，經常會用到方程思想解決問題。可以說，勾股定理和方程是絕配。下面提供幾個實例，供同學們學習研究。

一、直接求邊長，“源”來是方程

例1 在Rt△ABC中，∠ACB=90°，AB=10，BC=6，求AC的長。

解：由勾股定理，AC2+62=102。

解得AC=±8（負值舍去），∴AC=8。

【說明】本題由勾股定理得出的等式AC2+62=102，其中含有的AC就是一個未知數，可以看出方程思想的應用。

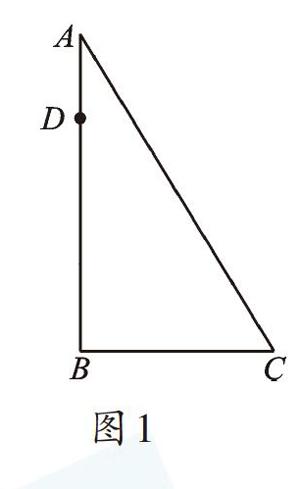
例2 如圖1，已知Rt△ABC中，∠ABC=90°，AB上有一點D，BD=10，BC=5，AD+AC=15，求斜邊AC的長。

圖1

解：設AC=x，則AD=15-x，AB=25-x。由勾股定理可得：

（25-x）2+52=x2，

解得x=13，∴AC=13。

【說明】由勾股定理可知BC2+AB2=AC2，其中BC邊為已知邊，邊AB上的線段BD的長已知，線段AD和AC之間有數量關系，可設未知數，并表示出AD、AC，利用勾股定理構造方程，即可求解。

二、巧設未知數列方程

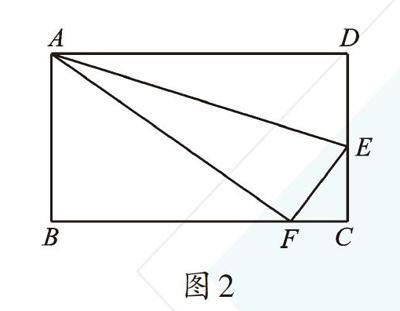
例3 如圖2，小紅用一張長方形紙片ABCD進行折疊，已知該紙片寬AB為8cm，長BC為10cm。當小紅折疊時，頂點D落在BC邊上的點F處（折痕為AE）。求△ECF的面積。

圖2

【分析】要求△ECF的面積，就需要求出Rt△ECF的直角邊CF和CE的長。

解：由題意可知，AF=AD=BC=10cm，

在Rt△ABF中，由勾股定理可得：

BF=[AF2-AB2]=[102-82]=6，

∴CF=BC-BF=4cm。

設CE=xcm，則EF=DE=（8-x）cm;在Rt△ECF中，由勾股定理可得：

42+x2=（8-x）2，解得x=3。

∴S△CEF=[12]CF·CE=[12]×3×4=6cm2。

【說明】本題同樣是考查方程思想在勾股定理中的應用。Rt△ECF的邊長CE和EF都是未知的量，我們通過設CE的長為x，就可以巧妙地表示出與之有關系的線段DE和EF的長，然后還是利用勾股定理構造方程解決問題。從中可以看出，勾股定理和方程果然是絕配啊。

三、構造直角三角形列方程

例4 如圖3，客輪沿折線A-B-C從A出發經B再到C勻速航行，貨輪從AC的中點D出發沿某一方向勻速直線航行，將一批物品送達客輪。兩船同時起航，并同時到達折線A-B-C上的某點E處。已知AB=BC=200海里，∠ABC=90°，客輪速度是貨輪速度的2倍。求貨輪從出發到兩船相遇共航行了多少海里？

【分析】由題意可分析得知客輪和貨輪的相遇點E必然在線段BC上且靠近點B處，為求出DE的長，需要自主構造所需的直角三角形，利用勾股定理解決問題。考慮到構造出的Rt△DEF有兩邊未知，因此還是需用方程解決問題。

圖3

解：過點D作DF⊥BC于點F，易得DF=CF=BF=100海里。設貨輪所行路程DE=x海里，可得客輪所行路程AB+BE=2x海里，于是EF=（300-2x）海里，在Rt△DEF中，有1002+（300-2x）2=x2。

解得：x=200±[10063]。

∵200+[10063]>100[2]（舍去），

∴DE=200-[10063]。

答：貨輪從出發到兩船相遇共航行了（200-[10063]）海里。

【說明】本題是一個較為復雜的實際應用問題，其難點有兩個：一是構造所需直角三角形;二是需要結合方程思想利用勾股定理求解，與前幾個例題不同的是列出的方程是一元二次方程。我們在用方程思想解決問題時，不僅要關注所設的未知數x，更要能較熟練地用含x的代數式表示等式中的其他數量。本題突破點就在于用含x的代數式表示線段EF的長。

其實，在很多幾何計算問題中，尤其是解決稍為復雜的問題時，方程思想往往是很重要的選擇。同學們在解題時要有方程意識，要善于利用問題中所給的數量關系，構造已知量與未知量之間的等量關系，列出方程解決問題。

（作者單位：江蘇省太倉市實驗中學）