側風狀態下剪刀型尾槳的氣動噪聲特性

代 軍 何 強 湯 艷 張 偉

（西南科技大學土木工程與建筑學院 四川綿陽 621010）

直升機作為一種能夠垂直起降、懸停、小速度飛行的飛行器，在民用和軍用等領域都有廣泛應用，但直升機噪聲較大的特點制約了其進一步應用。直升機的旋翼和尾槳通常是直升機氣動噪聲的主要來源。在特定的飛行狀態下，直升機尾槳噪聲會急劇增大，導致尾槳噪聲成為直升機總噪聲的主要來源［1］。

隨著計算機技術與數值計算方法的發展，計算流體力學（CFD）方法逐漸成為直升機噪聲研究的重要手段。對直升機旋翼和尾槳噪聲的研究分為尾槳流場的計算與氣動噪聲的計算。

旋翼數值計算方法的發展可以分為4個主要發展階段，每個階段所使用的方程分別是：小擾動方程、全位勢方程、Euler（歐拉）方程以及Navier-Stokes（N－S）方程。20世紀80年代中期，Roberts等［2］建立了一套適用于旋翼懸停流場的計算方法，該方法首次將歐拉方程運用到旋翼流場的求解中。西北工業大學的學者王立群等［3］用網格中心有限體積法對具有兩片槳葉的旋翼在亞聲速與跨聲速運動下的壓強分布進行了計算。童自力等［4］采用帶有動量源項的N－S方程，對不同構型的直升機旋翼的流場進行了模擬，并分別研究不同構型旋翼的氣動力特性。南京航空航天大學［5－6］、中國直升機設計研究所［7］等采用CFD方法對直升機尾槳氣動流場進行了研究。

目前，研究旋翼氣動噪聲的數值模擬方法中大多數都使用到了FW－H方程與Kirchhoff方程。20世紀60年代后期，英國的Williams等［8］提出了著名的FW－H方程，可以用于精確計算任意固體邊界與流體相互作用而產生的噪聲。20世紀80年代，Farassat［9］基于FW－H方程，經過一系列的推導，最終得到了Farassat 1公式，并在其基礎之上又導出了Farassat 1A公式。西北工業大學的韓忠華等［10］運用歐拉方程與FW－H方程對直升機旋翼懸停狀態與前飛狀態的聲場做了計算，并取得了較為理想的結果。王立群等［11］進行了直升機旋翼槳尖形狀對噪聲量級影響的研究。

剪刀型尾槳是一種常應用于武裝直升機的尾槳構型，其由上下兩對非等距、有間距排列的槳葉構成。由于其槳葉分布是不等距的，臨近的兩片槳葉在某些交疊角下間距會很小，導致兩片槳葉之間會有強烈的氣動干擾。已有研究表明，非等距角槳葉布置引起的“調制效應”使得剪刀型尾槳具有一定的降噪能力［1］。目前已有的研究主要是針對其懸停和前飛狀態的噪聲特性［12］。在側風狀態下，尾槳易進入渦環狀態導致尾槳氣動失效，而剪刀型尾槳特殊的幾何構型，使得其進入渦環狀態的運動行為更復雜，剪刀型尾槳流場的復雜性同時也導致了其氣動力和氣動噪聲特性的復雜性。據作者調研，目前尚未有針對剪刀式尾槳在側風狀態下的氣動力和氣動噪聲特性的系統研究。

基于此，本文運用計算流體力學的方法首先對直升機尾槳的流場進行計算模擬，得到必要的流場數據，再將尾槳流場數據輸入到噪聲計算模型中，對尾槳的氣動噪聲進行研究，分析側風狀態下剪刀型尾槳的幾何構型（軸向間距及交疊角）對尾槳氣動力和氣動噪聲特性的影響。

1 計算模型及方法

1.1 剪刀型尾槳模型

本文針對Lynx旋翼［13］來研究L型剪刀型尾槳的氣動力特性，其尺寸參數為：槳葉翼型采用NPL－9615，旋轉半徑（R）為1.105 m，弦長為0.180 m，無負扭轉，槳葉數為4。L型尾槳如圖1所示，其旋轉在前的槳葉低于旋轉在后的槳葉。

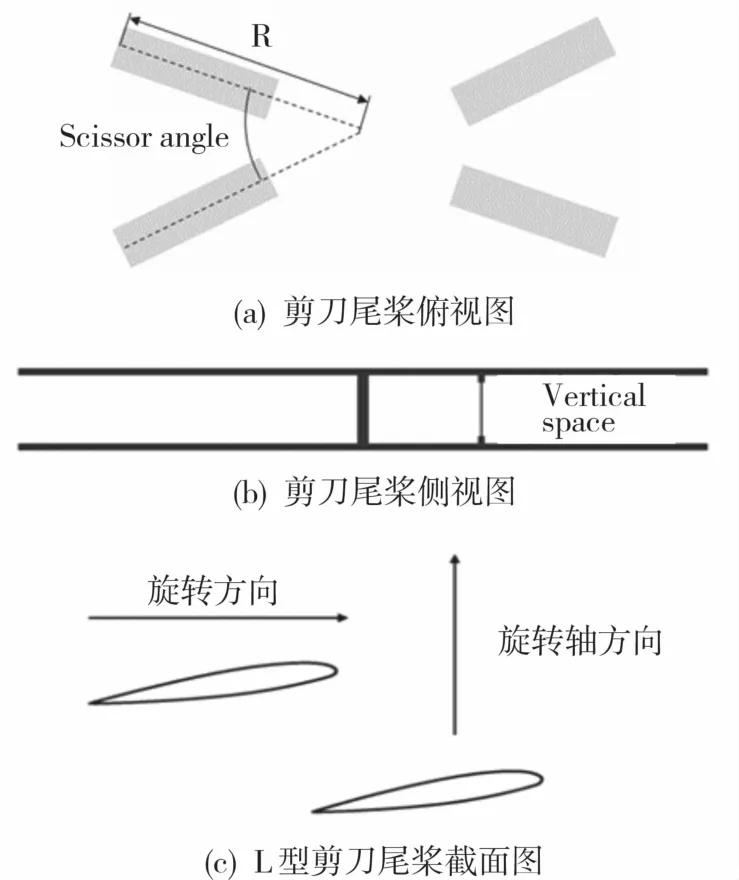
圖1 L型尾槳示意圖Fig.1 Schematic diagram of the L－shaped tail rotor

1.2 計算域

整個流域分為內部計算域與外部計算域，內域為直徑3 m、高0.3 m的圓柱狀流域，如圖2所示。外域為高100 m、底面邊長為150 m的方形區域，內域在距離進口30 m截面中心處，如圖3所示。

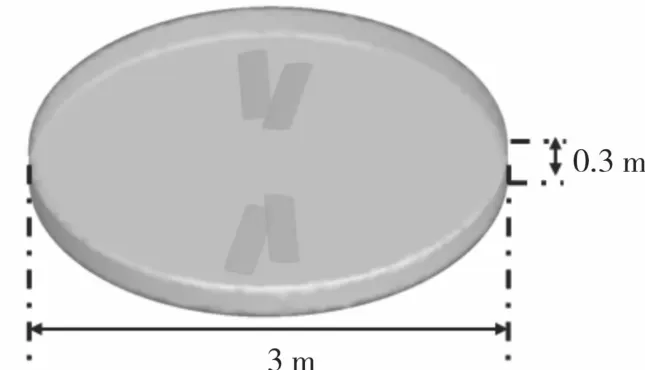
圖2 內流域示意圖Fig.2 Schematic diagram of the internal domain

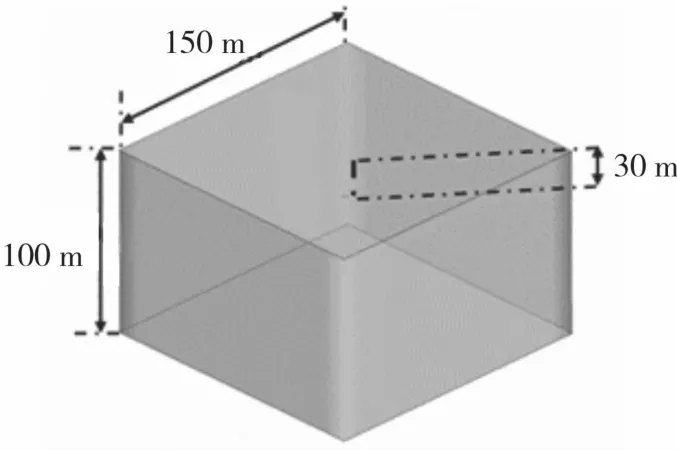
圖3 外流域示意圖Fig.3 Schematic diagram of the external domain

1.3 網格劃分及邊界設置

由于剪刀型尾槳結構較復雜，故采用混合網格進行網格劃分，即將整個計算域劃分為內部和外部兩個部分。內部小區域劃分為小尺寸的非結構網格，槳葉表面網格加密并添加邊界層網格（圖4）；外部區域采用結構網格（圖5及圖6）。經過網格收斂性驗證后，確定各算例總的網格數大約在700萬左右。

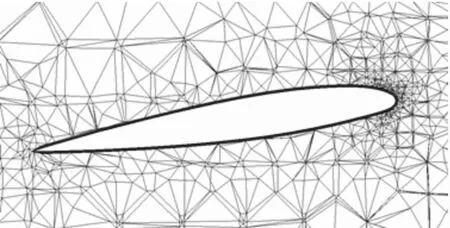
圖4 槳葉網格截面Fig.4 Grids around airfoil

圖5 內部流域非結構網格Fig.5 Unstructured grids ofinternal domain

圖6 外部流域結構網格及邊界條件Fig.6 Structured grids of external domainand boundary conditions

1.4 求解器設置

本次計算模擬采用密度基求解器，三維非定常計算。計算時選用k－ε湍流模型，內部計算域為旋轉區域，其角速度為184.6 rad／s，即槳尖馬赫數約為0.6，側風狀態時垂直于尾槳盤面的來流速度為10 m／s。采用滑移網格實現尾槳的旋轉運動，尾槳所在圓柱區域為內部運動區域，外部為靜止區域，內外計算域之間設置一對交界面，通過插值來實現動靜區域的數據傳遞。噪聲計算選用Ffowcs-Williams＆Hawkings噪聲模型，采用隱式的一階迎風格式，時間步長設置為0.000 472 66 s。

2 剪刀型尾槳氣動力特性

剪刀型尾槳有比常規尾槳更為復雜的結構，其氣動力特性會受到其構型的影響。交疊角與軸向間距都是影響因素，研究清楚剪刀型尾槳的交疊角與軸向間距對其氣動特性的具體影響對剪刀型尾槳的參數設計是非常重要的。

拉力為垂直于旋轉平面的向上的合力，此處采用無量綱化的拉力系數來描述，其定義為：

其中，T為尾槳拉力，ρ為來流密度，U為來流速度，S為槳葉的橫向截面積。

為了更好地研究相同間距下交疊角對剪刀型尾槳氣動力特性的影響，通過固定間距變化交疊角的方式進行計算。交疊角在0°～90°之間，每隔15°計算一個工況。圖7和圖8給出了軸向間距為0.1R和0.08R時的各交疊角的拉力系數隨時間變化圖，從圖中可以看出，拉力系數隨著迭代進行逐漸收斂達到穩定值。

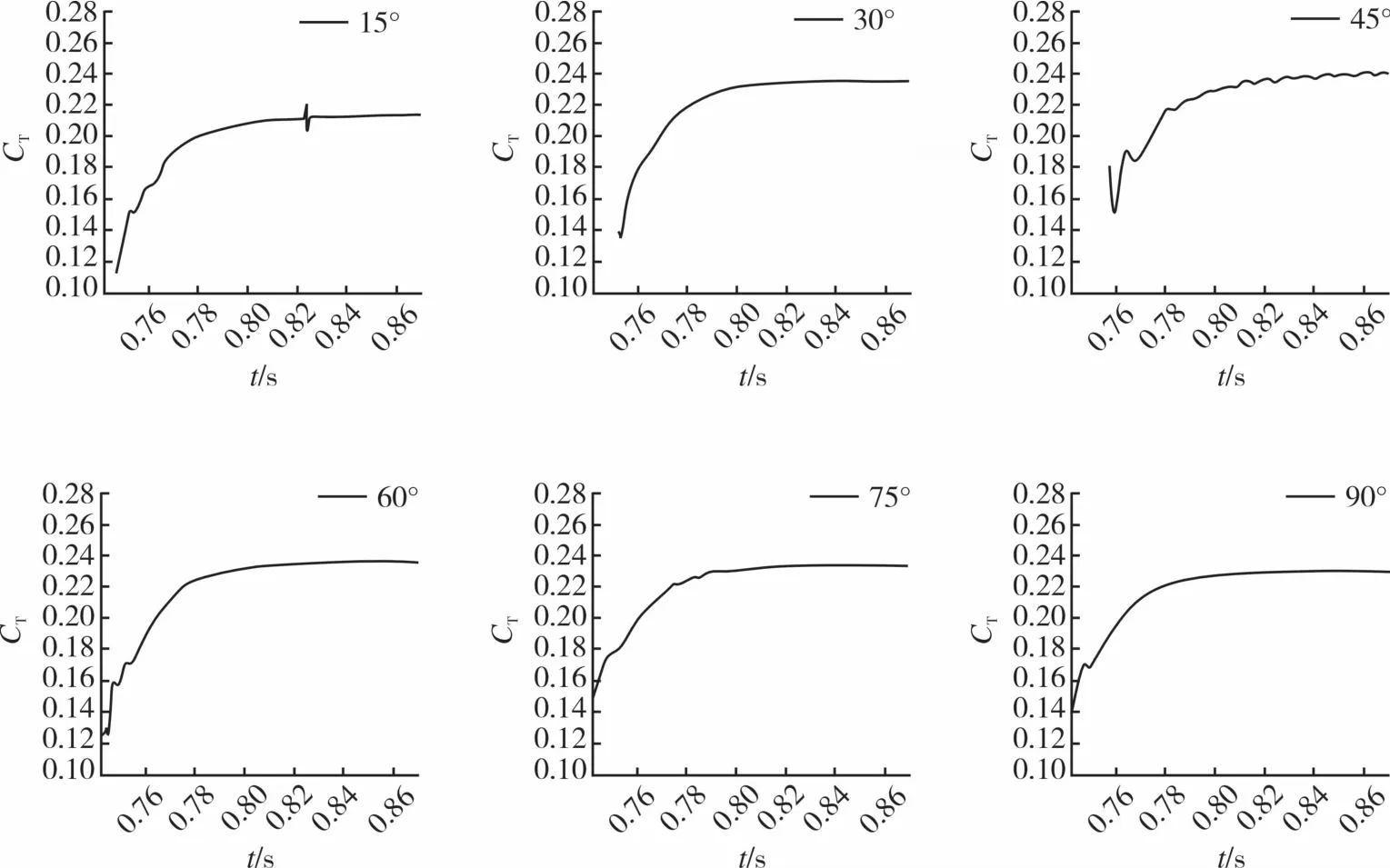
圖7 尾槳間距為0.1R的各交疊角的氣動力監測圖Fig.7 Aerodynamic monitoring diagram of each overlapping angle at a vertical space of 0.1R

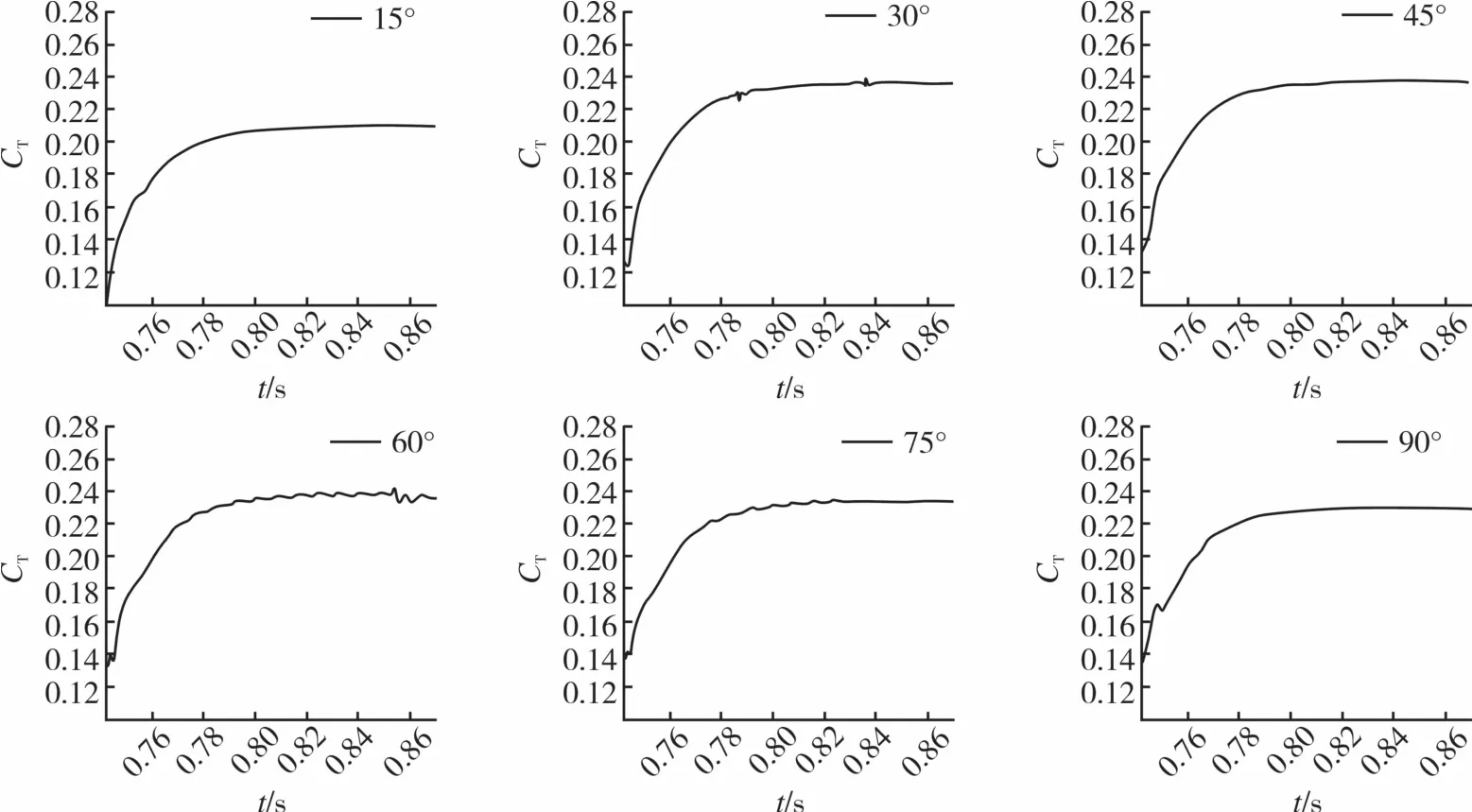
圖8 尾槳間距為0.08R的各交疊角的氣動力監測圖Fig.8 Aerodynamic monitoring diagram of each overlapping angle at a vertical space of 0.08R

圖9 給出了軸向間距為0.1R和0.08R時尾槳總的拉力系數隨交疊角變化的曲線圖。從圖9可以看出，兩種間距時尾槳氣動力隨交疊角的變化趨勢整體上是相似的，但是也略有差別。兩種間距時，交疊角為45°時垂直于旋轉面的拉力系數均是最大的。在交疊角45°之前時，拉力系數變化趨勢都是呈上升的，增長的速率較接近。0.1R間距的氣動力明顯是要大于0.08R間距的氣動力。45°之后兩組數據都減小，二者在減小的速率上有差別。

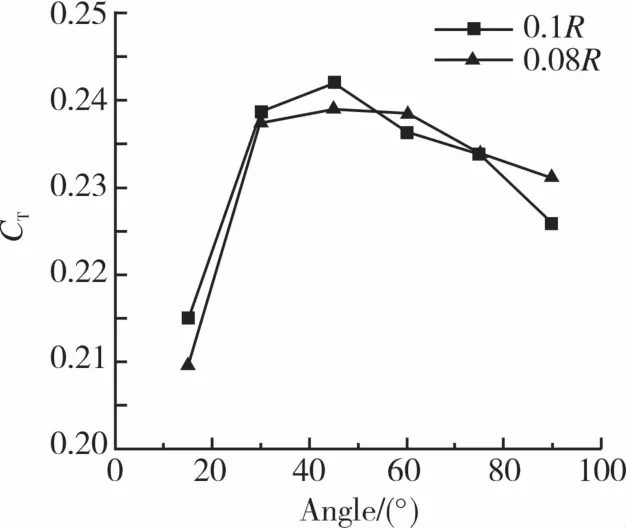
圖9 0.1R，0.08R間距下尾槳氣動力隨角度變化對比圖Fig.9 Comparison diagram of the aerodynamic changes of the tail rotor with the angle at vertical space of 0.1R and 0.08R

圖10 給出了間距分別為0.1R與0.08R的尾槳上下槳葉的氣動力對比圖（上面的槳葉標識為L－1，下面的槳葉標識為L－2）。從圖10可以看出，不管是間距為0.1R還是0.08R的尾槳，槳葉L－1的升力隨著交疊角的增大而增大，槳葉L－2的升力在30°附近之前隨著交疊角的增大而增大，30°之后槳葉L－2的升力隨著交疊角的增加而減小。

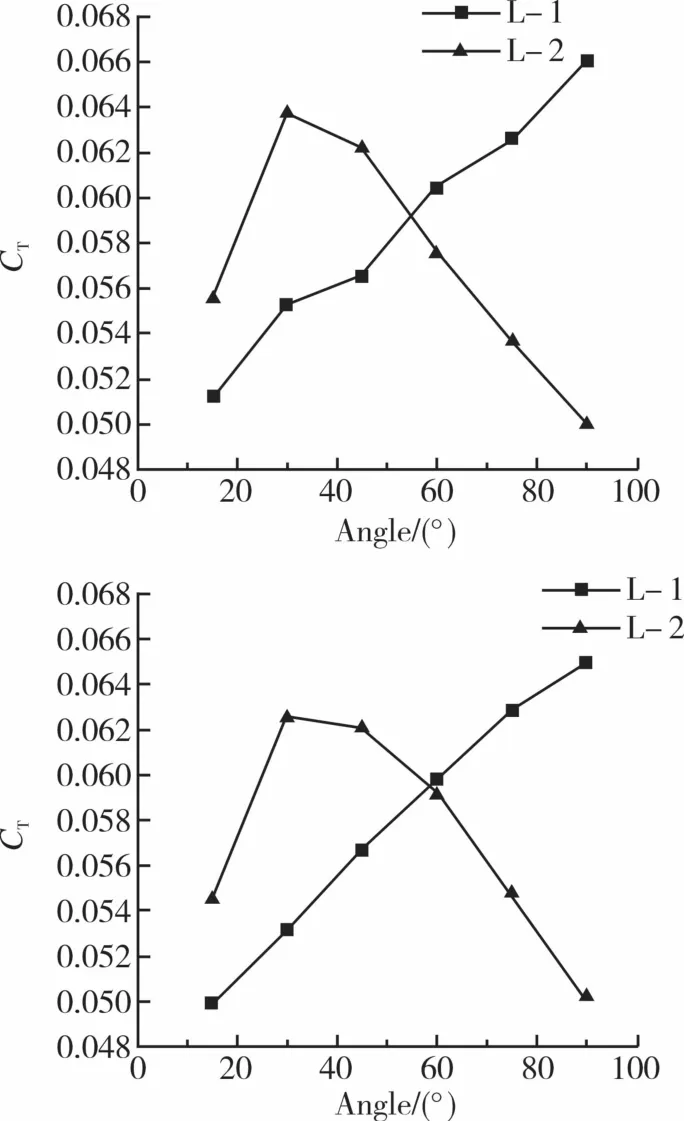
圖10 0.1R，0.08R間距時上下槳葉氣動力對比圖Fig.10 Aerodynamic contrast diagram of upper and lower blades at the space of 0.1R and 0.08R

出現這種現象的原因可以用槳－渦干擾來解釋。圖11和圖12分別給出了兩種間距時不同交疊角的渦量圖。當尾槳的交疊角為15°～45°時，可以看出尾槳L－2的槳尖渦干擾另一邊的尾槳L－1周圍的流動，而尾槳L－1距離尾槳L－2較遠，所以尾槳L－1的槳尖渦對尾槳L－2的干擾較小。在交疊角為15°時該現象最為嚴重，隨著角度的增大，干擾現象減弱，拉力隨之上升。當交疊角為45°～90°時，由于不同側的L－1與L－2之間的角度減小，此時尾槳L－1的槳尖渦對尾槳L－2的干擾明顯增強，而尾槳L－2與尾槳L－1的距離變大，干擾變小，總體升力隨之下降。到交疊角為90°時，前者的干擾現象最為明顯。

圖11 0.1R間距15°，30°，60°，75°交疊角的尾槳渦量圖Fig.11 Vorticity diagram of tail rotor at 0.1R overlapping angles of 15°，30°，60°and 75°

圖12 0.08R間距15°，30°，45°，60°，75°，90°交疊角的尾槳渦量圖Fig.12 Vorticity diagram of tail rotor at 0.08R overlapping angles of 15°，30°，60°and 75°

分析軸向間距對氣動力的影響，得到如下結論：軸向間距變小時，槳葉之間的距離會變得更小。在尾槳運動時，尾槳上下槳葉的槳－渦干擾會增強，所以小間距尾槳的氣動力整體上小于大間距尾槳的氣動力。

3 側風狀態下剪刀型尾槳氣動噪聲分析

3.1 氣動噪聲監測點布置

為計算尾槳在側風條件下的氣動噪聲，在計算過程中設置了5個監測點。按照此方式布置的監測點既能夠監測到旋轉平面的厚度噪聲，也能監測到來流所導致的噪聲的影響。圖13（z軸未畫出）總共有編號為1，2，3，4，5的5個監測點，其在圖上坐標系的坐標分別為：（3R，0，0），（5R，0，0），（7R，0，0），（5R，R，0），（5R，－2R，0）。R為槳葉的展長，為1.105 m。

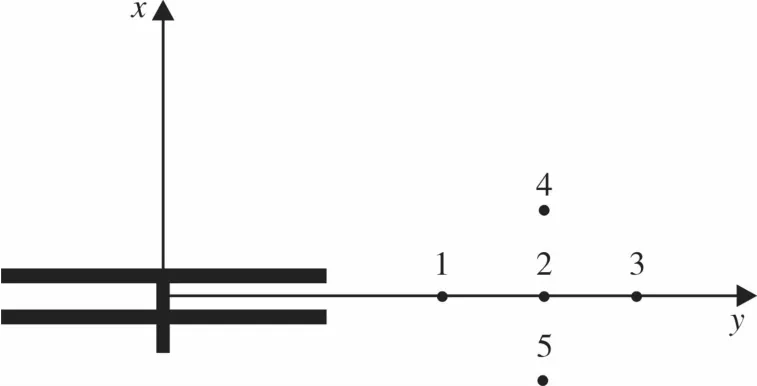
圖13 尾槳氣動噪聲監測點示意圖Fig.13 Schematic diagram of aerodynamic noise observation point

3.2 氣動噪聲求解設置

采用Ffowcs-Williams＆Hawkings噪聲模型計算尾槳噪聲，然后定義噪聲源為剪刀型尾槳的4片槳葉。設置保存噪聲數據文件為asd格式，并設置寫入頻率為2 Hz，每個聲學計算所保存的文件要包含100個時間步的計算數據。

3.3 剪刀型尾槳氣動噪聲特性

圖14 給出了間距為0.1R的各交疊角下監測點1的一個周期內的噪聲－時間歷程圖。由圖14可知：交疊角較小時，尾槳噪聲能量更加集中，其噪聲幅值也較大；當交疊角增大時，尾槳噪聲能量會逐漸分散直至出現多個噪聲峰值，其幅值也會有所降低。

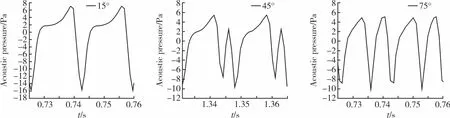
圖14 間距為0.1R的各角度下的一個周期內的噪聲－時間歷程圖Fig.14 Acoustic pressure－time history diagramat various angles with a spacing of 0.1R

圖15 給出了間距為0.1R的各交疊角下監測點1的噪聲－頻率圖。尾槳交疊角的不同，可以“調制”出多個槳葉通過頻率，從而改變了尾槳的噪聲頻譜，降低了尾槳的噪聲水平。尾槳在受到渦干擾的時候脈動減小，并且夾角越小越明顯。

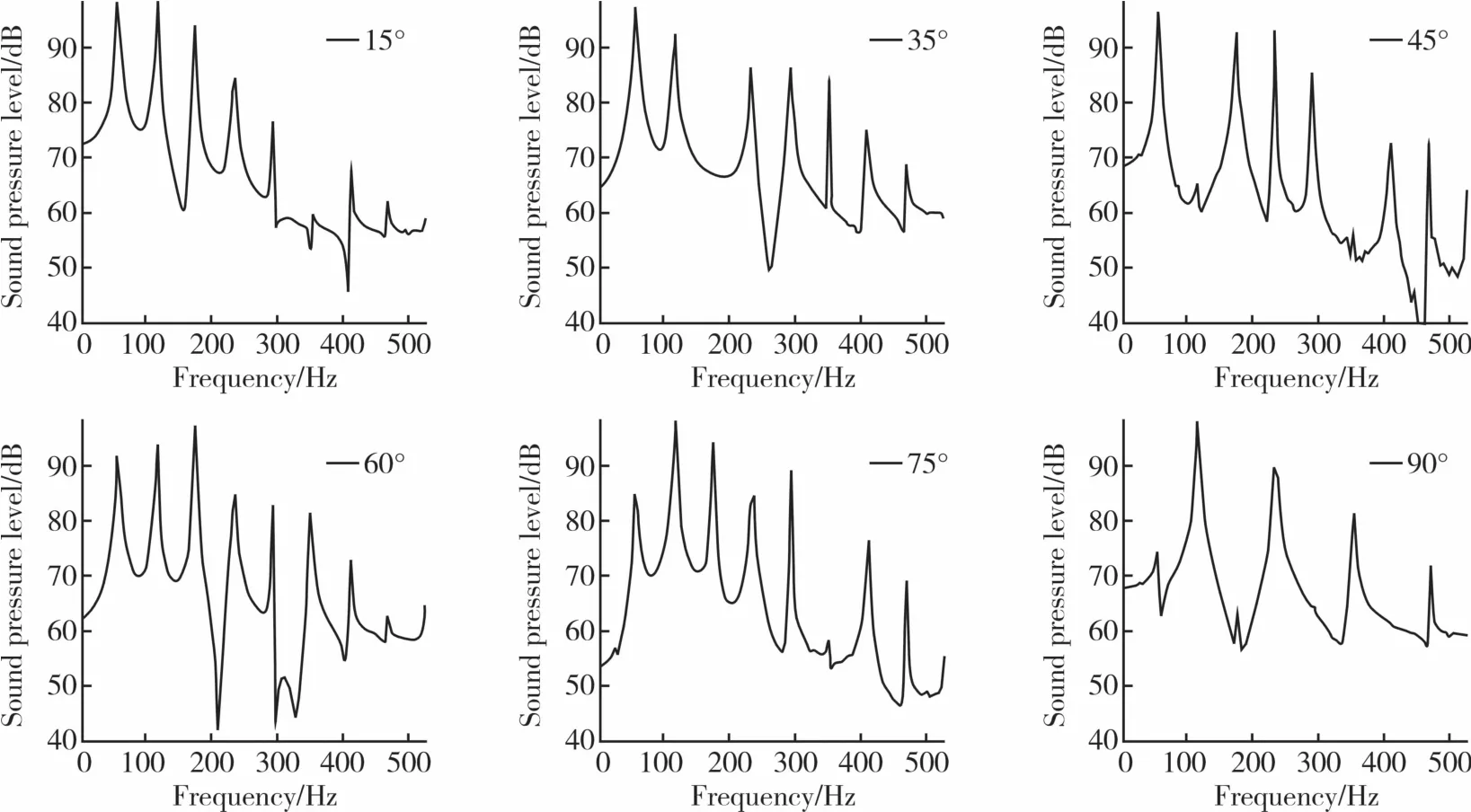
圖15 間距為0.1R的各角度下的噪聲－頻率圖Fig.15 Sound pressure level－frequency diagram at various angles with a spacing of 0.1R

圖16 給出了兩種間距時不同交疊角尾槳的5個監測點的氣動噪聲聲壓級數據。可以看出：當單獨考慮交疊角變化對氣動噪聲的影響時，剪刀型尾槳的氣動噪聲在15°～60°的范圍內都是隨著交疊角的增加而減小，變化趨勢較劇烈；當交疊角在60°～90°的范圍內時，氣動噪聲聲壓級的大小隨著交疊角變化的趨勢較平穩；軸向間距對噪聲聲壓級的影響不明顯。這樣的結果顯示的趨勢與前述的氣動力的變化趨勢有相似之處，說明尾槳上下槳葉的槳－渦干擾對噪聲有很大的影響。

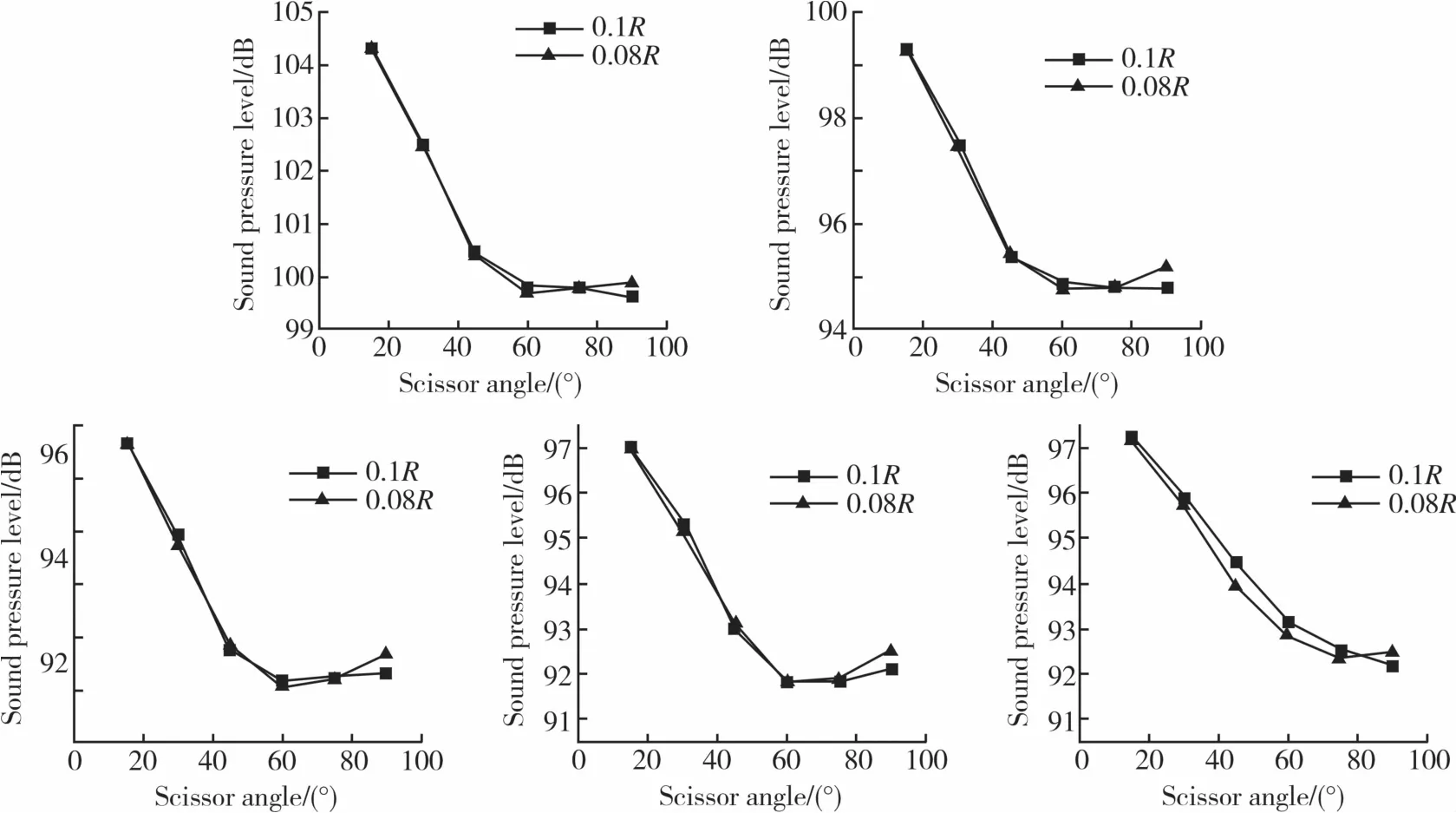
圖16 0.1R間距與0.08R間距時的氣動噪聲對比圖Fig.16 Comparison diagram of aerodynamic noise at vertical space of 0.1R and 0.08R

4 結論

本文對剪刀型尾槳的流場進行了計算，分析了其氣動力特性，在尾槳流場數據的基礎上，進行了尾槳氣動噪聲計算，得出以下主要結論：（1）尾槳氣動力計算結果表明，尾槳的拉力隨著交疊角的增大呈現先上升后下降的趨勢，45°時的尾槳拉力最大，但45°之后的尾槳拉力整體上大于45°之前的尾槳拉力，說明45°之前的槳－渦干擾要大于45°之后的情況。相比尾槳交疊角對尾槳氣動力的影響而言，軸向間距的影響較小，但是依舊可以看出軸向間距變小，導致60°之前尾槳的氣動力變小，而在60°之后，尾槳氣動力隨著間距的變小而變大。（2）尾槳氣動噪聲分析表明，剪刀型尾槳的氣動噪聲隨著交疊角的增大而減小，在60°之前的減小趨勢比60°之后的減小趨勢要大，其原因是：在60°之前尾槳的槳渦干擾是尾槳L－2的槳尖渦對L－1的干擾，其對氣動力的影響更大，對噪聲的影響也較大；60°之后，尾槳L－1的槳尖渦對尾槳L－2的干擾更嚴重，其對噪聲的影響比前者的影響小，變化趨勢較為平緩。尾槳軸向間距減小使得在側風情況下的噪聲變小，其原因是：由于間距減小，雖然槳葉的距離更近，但槳葉L－1的槳尖渦對L－2的干擾變小，使得小間距尾槳整體噪聲變小。