基于彈性理論的煤幫極限平衡區寬度確定方法探討

于遠祥，柯 達，王京濱，王賦宇，陳寶平

(西安科技大學 建筑與土木工程學院，陜西 西安 710054)

隨著淺部煤炭資源的逐步枯竭，對深部煤炭資源的開采利用成為解決能源問題的重要途徑。大量深埋回采巷道開挖后圍巖發生劇烈的冒頂、片幫及底臌等變形破壞，嚴重影響了煤礦的安全高效生產。由于巷道兩幫的煤體強度通常較頂底板巖層低，變形量顯著而成為巷道圍巖控制的重點和難點。長期以來，大量專家學者和現場技術人員對兩幫煤體的變形破壞范圍進行了深入研究。侯朝炯等[1]基于松散介質應力平衡理論研究了巷道煤幫與頂板界面上的應力分布規律及其極限平衡區寬度;鄭桂榮等[2]根據煤巷兩幫煤體的受力特點，通過簡化煤幫應力分布曲線，建立了煤幫破裂區厚度的理論計算公式;李樹清等[3]應用彈塑性極限平衡理論分析了錨注聯合支護條件下的煤幫塑性區寬度;于遠祥等[4]基于煤幫支承壓力的雙曲函數分布模型，提出了煤幫極限平衡區和破碎區的計算公式，并分析了煤幫極限平衡區寬度的主要影響因素;單仁亮等[5]指出巷道幫部的破壞主要由幫部薄弱體壓剪破壞與交界面滑移破壞共同作用導致;劉德峰等[6]考慮工程擾動和巖體地質強度對煤幫巖體在變形過程中的影響，建立了非線性摩爾庫倫準則，確定了煤幫滑移面正應力及其極限平衡區寬度;李延軍[7]討論了大跨度開切眼煤幫極限平衡區深入圍巖的最大深度;黃慶享等[8]基于巷道底板極限平衡深度計算模型，得到了巷幫極限平衡區寬度與巷道底板破壞深度成線性增長關系的規律。

上述專家學者從不同角度對巷道幫部巖體的變形破壞規律進行了系統深入的分析，所得研究成果對確定合理的巷道開挖及支護方案具有重要參考價值。工程實際中，由于巷道幫部巖體的變形破壞與其應力應變狀態密切相關，但從現有關于巷道幫部變形的研究中可以看出，基于巖體自身的應力應變極限條件來反演分析巷道幫部極限平衡區寬度的研究成果還較少。因此，筆者通過建立巷道煤幫在支撐壓力作用下的力學分析模型，運用彈性理論，從分析煤幫巖體的應力應變入手，結合煤幫巖體的變形特征來反演分析煤幫的極限平衡區寬度，并基于工程實例對所得結論進行驗證，為研究回采巷道兩幫穩定性及其控制措施提供新的思路。

1 巷道幫部煤體受力變形分析

1.1 煤幫力學分析模型的建立

巷道開挖后，圍巖應力發生重新分布并在其幫部形成支承壓力。在無支護情況下，在垂直支承壓力作用下幫部巖體將會依次出現破碎區、塑性區及彈性區3個區域，如圖1所示[9]。

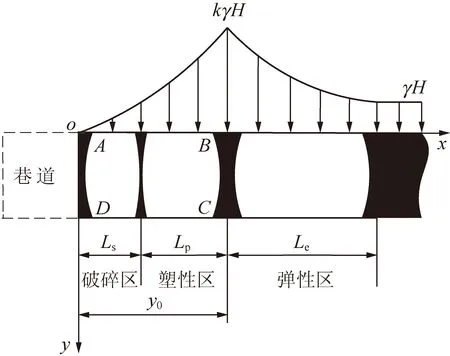
圖1 巷道煤幫支承壓力分布模型

為方便討論，將巷道煤幫上方支承壓力簡化為直線分布形式，如圖2所示。

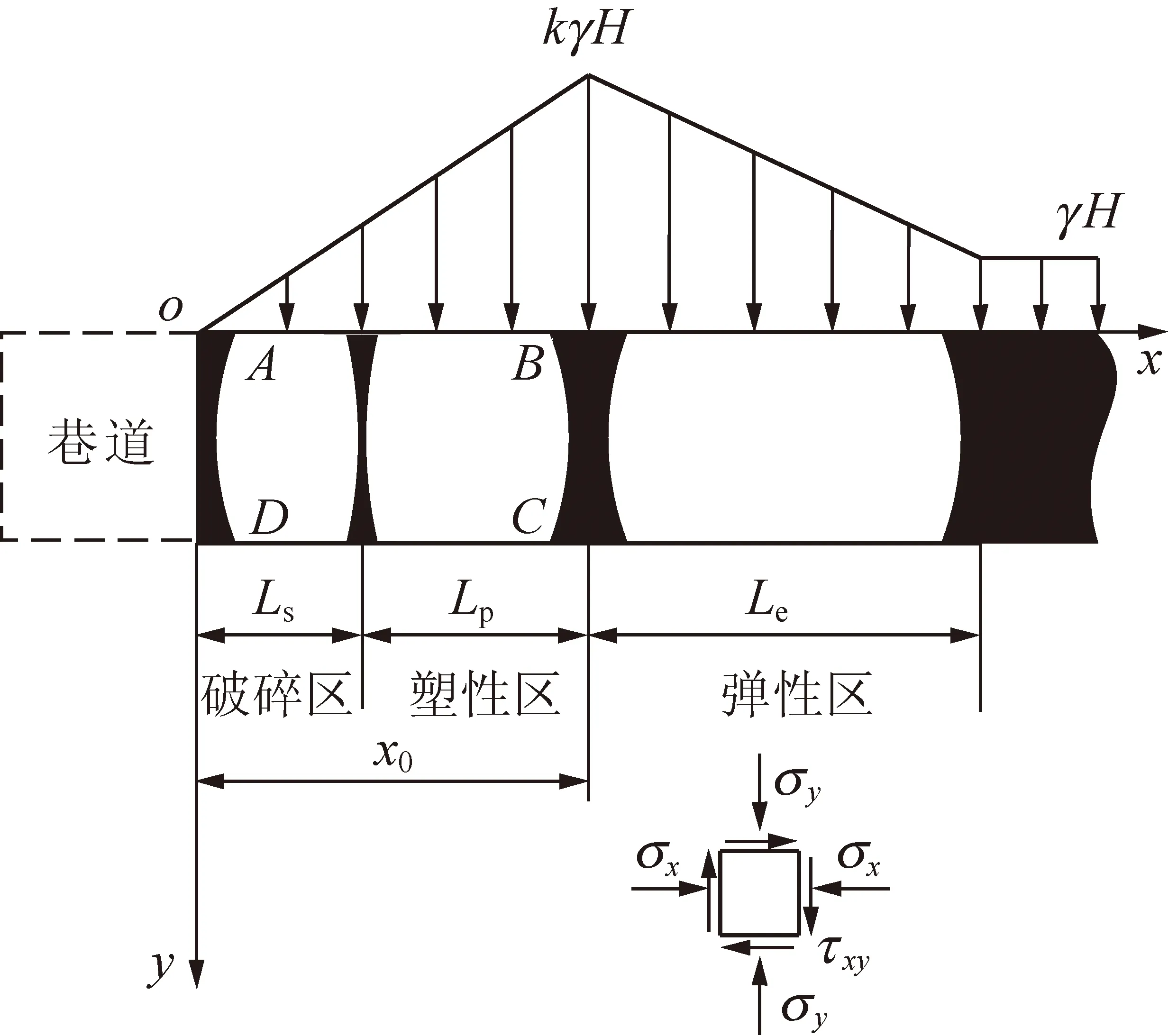
圖2 巷道煤幫支承壓力簡化模型

1.2 煤幫巖體變形計算原理

盡管巷道幫部巖體具有非連續、非均質且各向異性的物理力學特性，但由于開挖卸載所引起的巷道幫部巖體變形范圍通常較小，且直線分布形式能基本反映煤幫上方支承壓力的客觀分布規律，不妨設巷道幫部巖體連續、均質且各向同性，支承壓力按均勻荷載和線性荷載兩種工況進行疊加。在煤幫一定范圍內任取一單元體作為研究對象，根據半無限體在法向荷載作用下各應力分量的分析原理，分別計算各部分荷載作用下該單元體產生的各應力分量σx，σy及τxy，然后將各應力分量進行疊加即可求得煤幫內任一點的應力分量[10-11]。建立均勻分布荷載和線性分布荷載作用下巷道煤幫內任一點的受力模型如圖3所示和圖4所示。由彈性理論可知均勻分布荷載下煤幫巖體中任一點的應力分量分別為

(1)

(2)

(3)

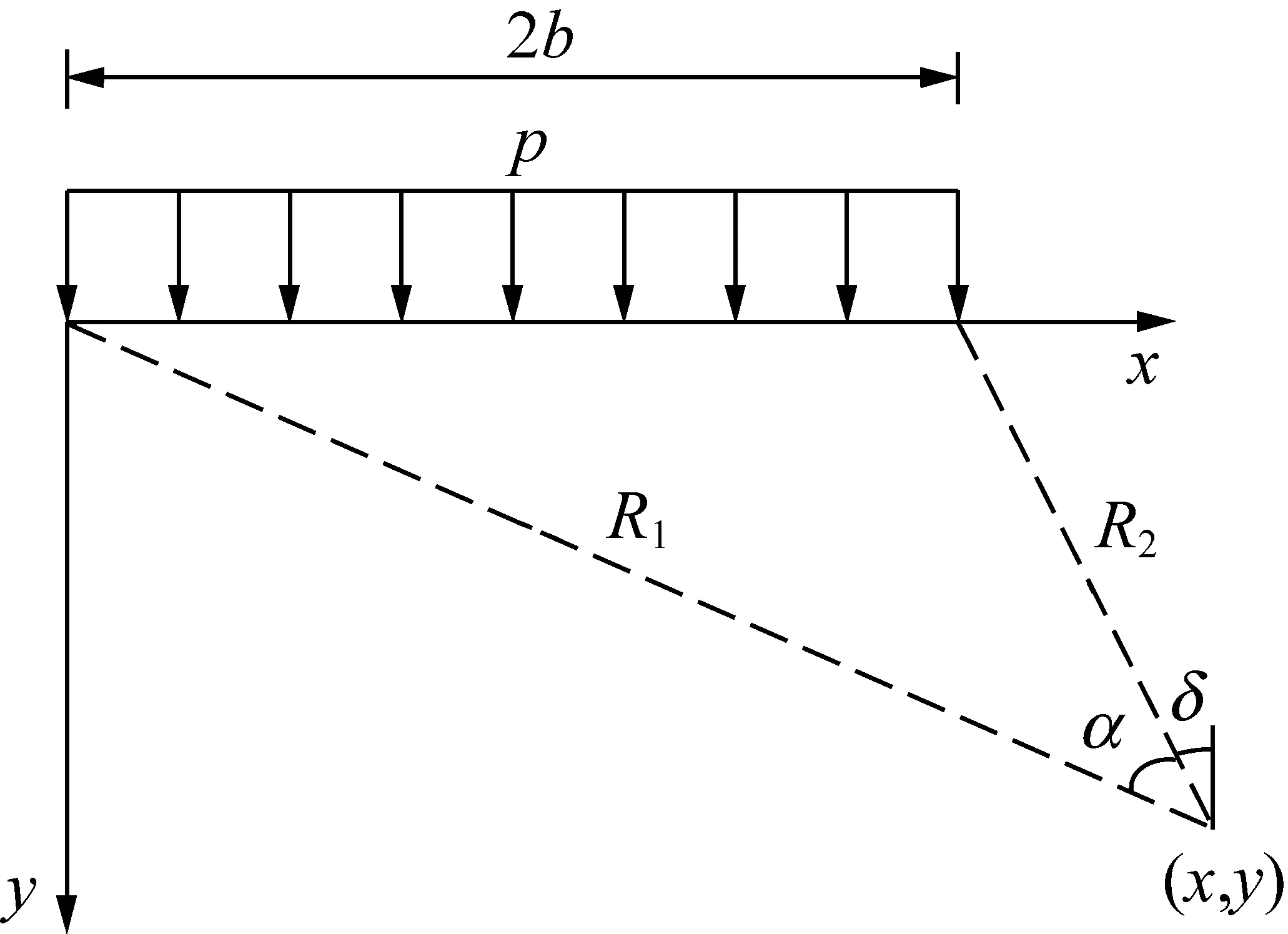
圖3 均勻分布荷載

同理，線性分布荷載下煤幫巖體中任一點的應力分量分別為

(4)

(5)

(6)

圖4 線性分布荷載

1.3 煤幫巖體應力分量的確定

將式(1)～(6)中的所有變量采用直角坐標值x和y表示。令峰值應力P1=kγH，P0=γH，按荷載分布形式，將圖2所示巷道煤幫支承壓力簡化模型劃分為3個部分，各部分應力分量計算如下:

(1)極限平衡區線性荷載

煤幫極限平衡區線性荷載計算模型如圖5所示。由式(4)～(6)可得該區內任一點的應力分量為

(7)

(8)

(9)

(2)彈性區均布荷載

煤幫彈性區均布荷載計算模型如圖6所示。由式(1)～(3)可得該區內任一點的應力分量為

(10)

(11)

(12)

圖5 極限平衡區線性荷載計算模型

圖6 彈性區均布荷載計算模型

(3)彈性區線性荷載

煤幫彈性區線性荷載計算模型如圖7所示。由式(4)～(6)可得該區內任一點的應力分量為

(13)

(14)

(15)

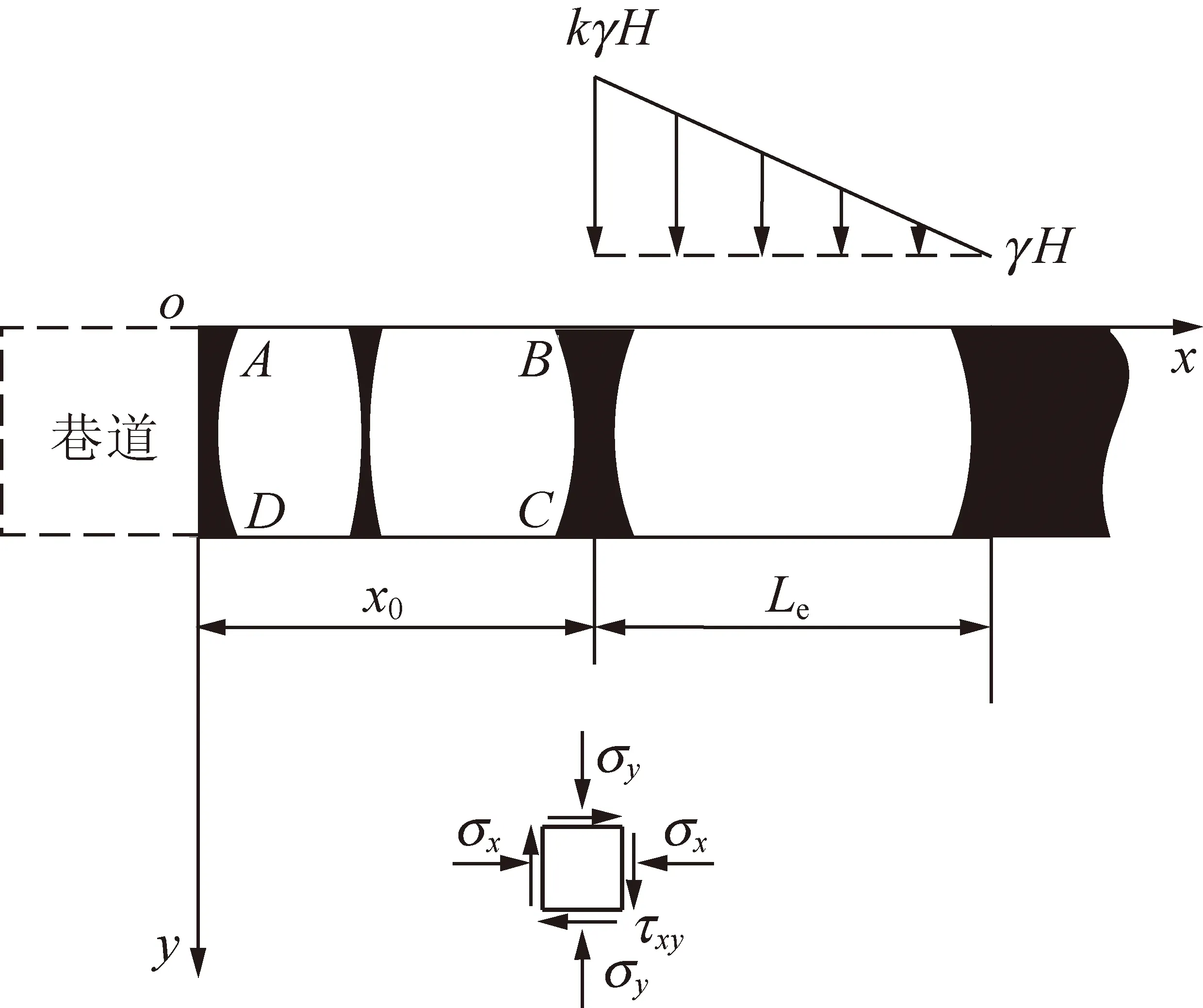
圖7 彈性區線性荷載計算模型

1.4 煤幫巖體應力應變分析

通過確定煤幫巖體內任一點在各部分支承壓力作用下的應力分量，由彈性力學理論可得該點的應力分量大小為

(16)

將巷道煤幫巖體簡化為均質連續的彈性體，根據虎克定律可得煤幫巖體內任一點的應變分量為

(17)

式中,E,μ分別為煤幫巖體的綜合彈性模量和泊松比。

2 巷道煤幫極限平衡區寬度分析

2.1 支承壓力下煤幫巖體柱條模型的建立

工程實際中，巷道開挖后，煤幫巖體在較大的豎向支承壓力作用下向巷道內產生膨脹變形，進而導致煤幫巖體出現朝向巷道內的徑向拉應變，該應變值隨支承壓力的增加而不斷增大。對某一具體界面上的煤幫巖體而言，其在支承壓力下的變形破壞具有明顯的“壓縮柱條”撓曲特征，如圖8所示。

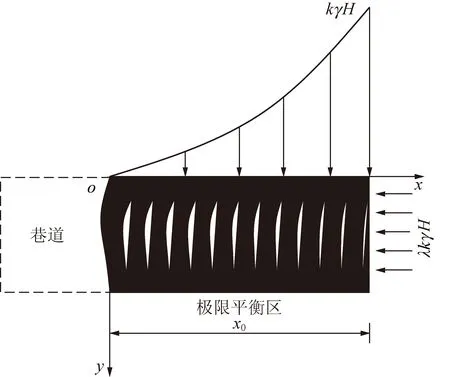
圖8 煤幫巖體“壓縮柱條”分析模型

當煤幫彈塑性界面上的巖體在其上方支承壓力作用下產生的徑向拉應變達到其極限拉應變時，該界面上“壓縮柱條”巖體將均處于撓曲斷裂的臨界狀態。由于煤幫上方支承壓力的連續分布，在由彈塑性界面至煤幫表面的不同界面上，“壓縮柱條”巖體所發生的撓曲變形量逐漸增大，多個并列“壓縮柱條”巖體的徑向撓曲變形連續疊加并在煤幫表面產生“幫臌”，最終在煤幫一定深度范圍內形成一個連續的極限平衡區[12-14]。

2.2 煤幫巖體撓曲斷裂力學分析

以煤幫彈塑性界面巖體為研究對象，忽略該界面巖體自重及其在垂直方向上的壓縮變形，建立支承壓力下彈塑性界面巖體的的“壓縮柱條”模型如圖9所示。

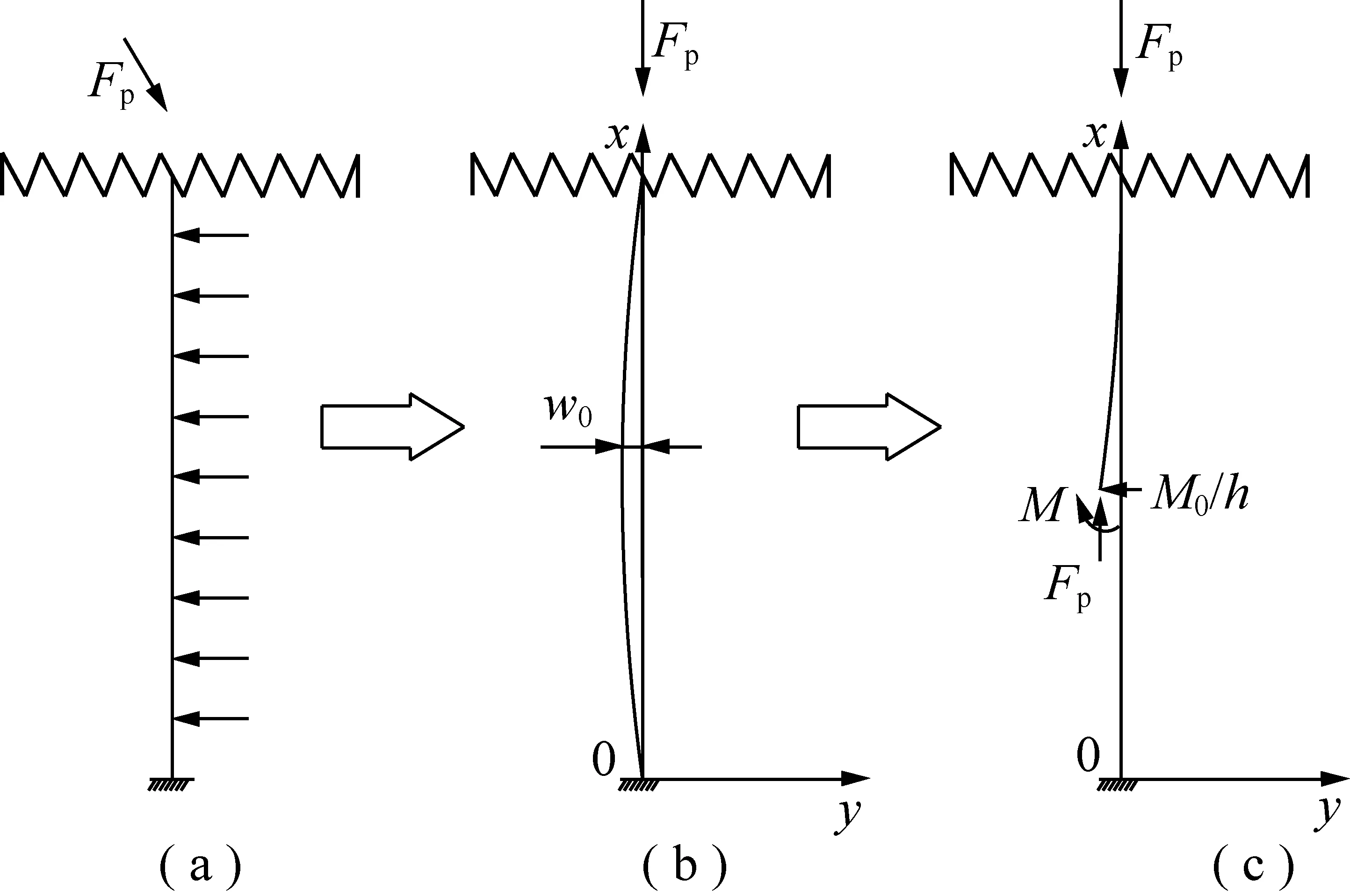
圖9 煤幫彈塑性界面巖體“壓縮柱條”模型

如圖9(c)所示，取x截面以下部分為分離體，以x截面的形心為中心建立力矩平衡方程得:

(18)

式中，M為x截面形心的彎矩;Fp為煤壁所受垂直方向壓力;w為煤壁撓度;M0為煤壁固定端力矩;h為巷道設計高度。

由材料力學理論[15]可知

M=-EIw″

(19)

式中，EI為煤壁的彎矩剛度。

由式(18)和(19)可得

(20)

令

(21)

則由式(20)和(21)可得

(22)

微分方程(22)的通解為

(23)

式中，c1和c2均為微分方程的通解系數。

由圖9可知壓縮柱條變形的邊界條件為

(24)

由式(23)和(24)可得

(25)

將式(23)代入式(21)得:

(26)

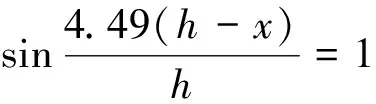
(27)

式中，k∈Z。

解之得:

x=(-1.39k+0.65)h

(28)

考慮x≥0的實際情況，當k=0時，有

x=0.65h

(29)

式(29)表明，煤幫彈塑性界面上的“壓縮柱條”巖體在支承壓力作用下的水平撓曲變形曲線為正弦半波，其水平撓曲位移的最大值位于距離底板0.65h處。當該點巖體發生的水平拉應變達到其極限拉應變時，“壓縮柱條”巖體將進入撓曲斷裂臨界狀態，這與文獻[8，16-17]的研究結果相吻合。

2.3 煤幫極限平衡區寬度計算

由上述分析可以看出，在煤幫彈塑性界面上發生最大水平撓曲位移的單元體位于(x0,0.35h)，將其坐標(x0,0.35h)代入式(7),(8),(10),(11),(13)及(14)得該單元在各部分支承壓力作用下的應力分量分別為

(30)

(31)

(32)

將式(30)～(32)代入式(16)得煤幫彈塑性界面上具有最大水平位移的單元巖體的應力分量為

(33)

(34)

對于峰值支承壓力下的煤幫彈塑性界面而言，發生最大水平應變的單元煤體的水平拉應變將達到其極限拉應變，由式(17),(33)及(34)得

(35)

由式(35)可以看出，巷道煤幫極限平衡區寬度是一個關于煤幫巖體極限拉應變的隱函數，其大小不僅取決于煤體的極限拉應變、泊松比及彈性模量，而且與原巖應力大小及巷道開挖后發生重分布的峰值應力水平及煤幫彈性區寬度密切相關。

2.4 煤幫極限平衡區寬度影響因素分析

(1)極限平衡區寬度與巖體彈性模量的關系

參考文獻[1]及[18-20]所述圍巖物理力學參數，設某回采巷道埋深H=600 m，其上覆巖層容重γ=25 kN/m3，煤幫巖體的平均泊松比μ=0.3，極限拉應變εtmax=0.35×10-3，煤幫彈塑性界面上應力集中系數K=1.5，將上述參數代入式(35)可得

arctan(0.715x0)+0.585]×109

(36)

由式(36)可得煤幫極限平衡區寬度與巖體綜合彈性模量的關系如圖10所示。

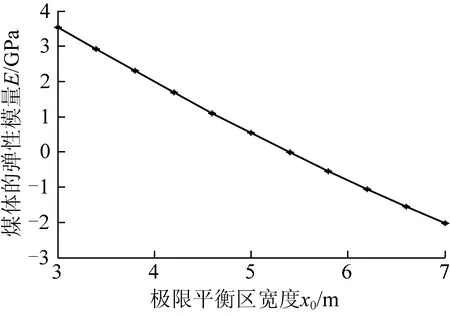
圖10 煤幫極限平衡區與巖體彈性模量的關系

(2)極限平衡區寬度與巖體極限拉應變的關系

當巷道煤幫相關參數分別為:H=600 m，γ=25 kN/m3，μ=0.3，K=1.5，E=3.4 GPa，由式(35)可得

11arctan(0.715x0)+0.6}×10-4

(37)

由式(37)可得煤幫極限平衡區寬度與巖體極限拉應變的關系如圖11所示。

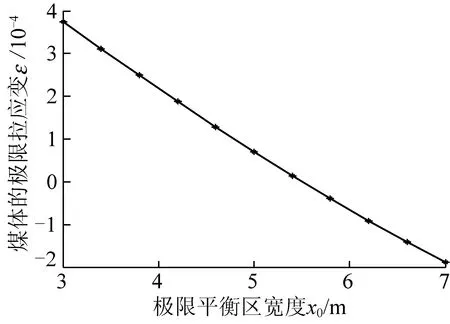
圖11 煤幫極限平衡區與巖體極限拉應變的關系

(3)極限平衡區寬度與巷道埋深的關系

同理，當巷道煤幫相關參數分別為:H=600 m，γ=25 kN/m3，εtmax=0.35×10-3，μ=0.3，K=1.5，E=3.4 GPa，由式(35)可得

13.7arctan(0.715x0)-0.75]

(38)

由式(38)可得煤幫極限平衡區寬度與巷道埋深的關系如圖12所示。

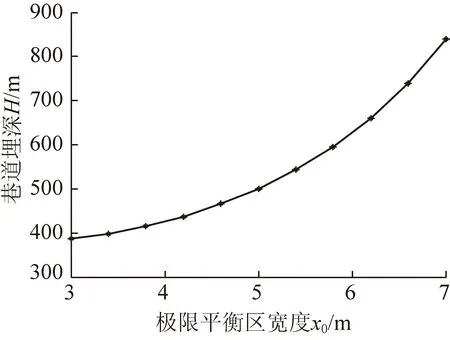
圖12 煤幫極限平衡區與巷道埋深的關系

3 巷道煤幫破裂區寬度計算

由文獻[4]可知，回采巷道開挖后，煤幫處于二向受壓狀態，承載能力大幅度降低。與此同時，由于應力集中，煤幫受力急劇增加，當煤幫表面巖體所受壓應力超過其極限強度時，表面巖體將由塑性狀態進入破裂狀態，形成如圖1所示的破裂區，其寬度為

(39)

式中，系數β和B分別由下式確定:

(40)

式中，c0,φ0及Ks分別為巷道煤幫與頂底板界面的黏聚力、內摩擦角及剪切剛度系數;N為煤幫彈塑性界面上所受的水平推力，其大小為

N=λkγHh

(41)

式中，λ為煤幫彈塑性界面上的側壓力系數。

此時，巷道煤幫塑性區寬度為

Lp=x0-Ls

(42)

4 算例分析

4.1 工程概況

陜西澄合百良煤礦4號主采煤層14501工作面運輸巷設計為4 000 mm×4 600 mm的矩形斷面，平均埋深為600 m，在運輸巷350～450 m里程處，由于幫部煤體整體強度較低，盡管開挖初期對巷道圍巖采取了高強度的錨桿(索)支護(圖13)，但仍然出現了嚴重幫臌和頂板下沉變形，兩幫收斂速率高達40～45 mm/d，嚴重影響了后期回采工作的正常開展。

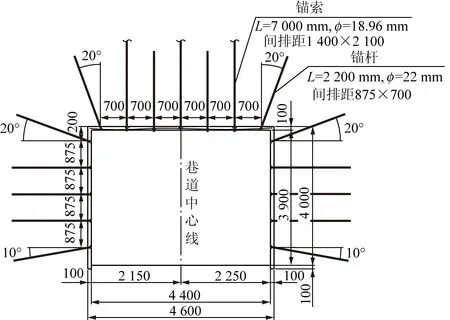
圖13 14501工作面運輸巷原支護方案

本文將根據上述理論公式確定14501工作面運輸巷煤幫的極限平衡區及其破裂區，進而對巷道圍巖的原支護參數進行優化。

4.2 14501工作面運輸巷煤幫變形分析

(1)煤幫極限平衡區寬度分析

經現場測試和工程類比，百良礦巷道煤幫巖體各參數的取值見表1。

表1 煤幫各計算參數取值

Table 1 Value of calculating parameters of coal wall

參數γ/(kN·m-3)Ks/(GPa·m-1)c0/MPaφ0/(°)λkE/GPaμεtmax/10-3取值250.143.0270.751.53.40.150.35

在14501工作面運輸巷350～450 m段開挖前后，煤幫上方原巖應力和支撐壓力峰值大小分別為

P0=γH=25×103×600=1.5×107Pa

(43)

P1=1.5×25×103×600=2.25×107Pa

(44)

設煤幫彈性區寬度為巷道設計高度，將式(43)和(44)代入式(33)和(34)得

(45)

(46)

將表1中相關參數、式(45)及(46)代入式(35)并化簡得

1.1arctan(0.715x0)+0.32

(47)

由式(47)即可解得14501運輸巷350～450 m段煤幫的極限平衡區寬度為x0=3.2 m。

(2)煤幫破裂區寬度分析

將表1中相關參數代入式(40)和(41)可得

(48)

N=0.75×1.5×25×103×600×4=

6.75×107N

(49)

103×600tan 27°)=1.03

(50)

將式(50)代入式(39)得煤幫破裂區寬度為

(51)

上述計算表明，14501工作面運輸巷350～450 m段巷道幫部錨桿未錨入塑性區，導致幫部巖體嚴重變形。在將幫部錨桿長度由2.2 m調整到2.8 m后，現場監測結果表明，巷道幫部巖體的收斂速率大大降低，頂底板穩定狀態得以顯著改善。

5 結 論

(1)本文以彈性理論為基礎，將巷道幫部巖體簡化為均質、連續的介質，通過建立支承壓力下回采巷道煤幫的受力模型，推導了煤幫巖體的應力應變解析解公式，為客觀反映煤幫巖體的變形破壞規律提供了理論依據。

(2)基于煤幫彈塑性界面巖體在支承壓力下的壓縮柱條模型，根據材料力學理論，建立了該界面巖體所產生的徑向極限拉應變與煤幫極限平衡區寬度的理論公式，結果表明:極限平衡區寬度與煤幫巖體的彈性模量及其極限拉應變呈反相關，與巷道埋深呈正相關關系。

(3)工程實例分析表明，本文提出的相關理論公式具有一定的科學合理性，能夠較好地闡述巷道幫部變形的力學原理，對深埋礦山巷道甚至其他地下硐室施工具有一定的參考價值。