高性能二元收斂噴管型面設計方法

李 娜，吉洪湖

（1.南京工業大學能源科學與工程學院，南京211800；2.南京航空航天大學能源與動力學院，南京210016）

0 引言

在滿足航空發動機推力性能設計要求的同時，噴管設計還希望獲得高效率，以提高發動機的單位推力，降低耗油率。二元收斂噴管取代傳統軸對稱收斂噴管能夠獲得相對更好的紅外隱身效果[1-3]，但卻犧牲了氣動效率[4-7]。為此，需開展高性能參數二元收斂噴管型面設計方法研究。二元收斂噴管型面設計是指在噴管進、出口截面幾何參數（進、出口截面面積和出口寬高比等）和噴管長度給定的情況下，根據噴管型面可以采用的描述方式，構造1個從發動機渦輪出口圓形截面光順過渡到噴管出口矩形截面的高性能二元收斂噴管型面。采用縱向型線的描述方法難以得到合理控制和設計，而采用垂直于噴管軸線的橫截面來描述[8-13]，各橫截面形狀連續變化，可以形成光滑過渡的二元收斂噴管型面。20世紀80年代，文獻[14]利用超橢圓方程可同時描述圓形至矩形等不同形狀截面的特點，用于設計二元噴管的圓形到矩形轉換段；文獻[15]介紹了1種采用圓角矩形（4個直角采用圓弧過渡的矩形）設計超聲速風洞圓形到矩形收斂段的方法。當選取不同的幾何參數值時，圓角矩形也可以以統一方式描述從圓形到矩形連續變化的不同橫截面形狀，也可以用于設計二元收斂噴管型面。

本文借鑒超橢圓和圓角矩形的上述優點以及前人設計經驗，發展和完善了基于超橢圓和圓角矩形截面的二元收斂噴管型面設計方法，并對橫截面控制參數與沿程變化規律之間的幾何約束關系進行探討分析。

1 基于橫截面的二元收斂噴管型面設計方法

1.1 基于超橢圓的二元收斂噴管橫截面設計

1.1.1 超橢圓截面描述方法

圓轉矩形的不同形狀橫截面如圖1所示。若采用超橢圓方程描述圖1中二元收斂噴管軸向任意x處的橫截面，在y-z平面內，超橢圓方程為

圖1 圓形轉矩形的不同形狀橫截面

式中：a、b分別為超橢圓截面的長、短軸半徑；η為超橢圓截面的可變指數。

當a=b，η→+∞時，式（1）描述的截面為圓截面；當η→+∞時，式（1）描述的截面形狀逐漸趨近于方形或矩形。理論上，η趨于無窮大，超橢圓方程才能描述嚴格的直角矩形截面。但實際應用時，采用超橢圓截面設計二元收斂噴管時，出口截面不宜設計為嚴格的直角矩形，可以取η為較大的數（如50）來設計噴口矩形截面。

1.1.2 超橢圓截面控制參數

對任意超橢圓截面，當給定a、b、η時，超橢圓截面形狀和面積完全確定，面積A為

式中：Г（·）為伽馬函數

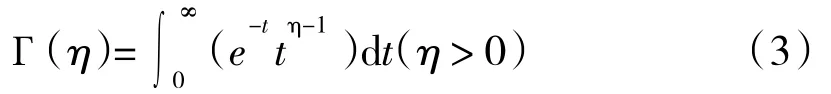
1.1.3 二元收斂噴管進、出口截面的超橢圓參數

在給定噴管進、出口截面幾何參數（進、出口截面面積和出口寬高比等）和噴管長度的情況下，采用超橢圓截面設計二元收斂噴管型面，首先需要計算進、出口截面的超橢圓參數值。

假設二元收斂噴管進口圓截面面積為A7，進口圓截面直徑D7=2，那么進口圓截面的超橢圓參數為

假設噴管出口截面面積（喉道面積）為A8、出口寬高比為AR（AR=a/b），同時假設出口截面為指數為ηe（取較大的數，如取ηe=50）的超橢圓截面，那么出口截面的其他超橢圓參數為

1.2 基于圓角矩形的二元收斂噴管橫截面設計

1.2.1 圓角矩形截面描述方法

若采用圓角矩形描述二元收斂噴管軸向任意x處的橫截面，在y-z平面內，圓角矩形可采用幾何形狀和參數來統一描述，如圖2所示。從圖中可見，圓角矩形4個直角均采用1/4圓弧過渡，a為圓角矩形的半寬，b為圓角矩形的半高，r為頂角圓弧半徑。顯然，當a=b=r時，圓角矩形變為圓，當r=0時，變為直角矩形。

圖2 圓角矩形截面形狀及參數

若采用數學方程來描述圖2中的圓角矩形，那么在y-z平面第I象限內，圓角矩形方程可分段表示為

1.2.2 圓角矩形截面控制參數

對任意圓角矩形截面，當給定a、b和r時，圓角矩形的形狀和面積完全確定，面積A為

若給定a、b和A，頂角圓弧半徑r可由式（13）惟一確定

1.2.3 二元收斂噴管進、出口截面圓角矩形參數

采用圓角矩形截面設計二元收斂噴管時，進口圓截面的圓角矩形參數為

當出口截面為嚴格直角矩形時，出口截面的圓角矩形參數為

當出口截面采用頂角圓弧半徑為re（＞0）的圓角矩形時，出口截面的其他圓角矩形參數為

1.3 二元收斂噴管橫截面控制參數沿程變化規律設計

為了使采用超橢圓或圓角矩形橫截面設計的二元收斂噴管具有高的氣動性能，需要對噴管截面控制參數沿程變化規律進行設計和控制。

假設噴管截面控制參數為p，p沿噴管軸向（x軸）的分布規律用函數p（x）表示，那么在進、出口截面控制參數值均已知的情況下（假設進口截面控制參數值為Pin，出口截面控制參數值為Pe），參數p的沿程變化規律p（x）可表示為插值函數形式

式中：x0為進口截面位置；L為噴管長度；φp（x）為截面相對位置x=（x-x0）/L的函數，且滿足條件：φp（0）=0，φp（1）=1。

因此，在噴管進、出口截面參數已知的情況下，噴管截面控制參數沿程變化規律p（x）的設計可轉變為截面位置函數φp（x）的構造和設計。

在給定噴管進、出口截面幾何參數（進、出口截面面積和出口寬高比等）和噴管長度的情況下，無論采用超橢圓還是圓角矩形來描述二元收斂噴管的橫截面形狀，進、出口截面參數均是已知的。因此，φ（p0）=0和 φ（p1）=1是函數 φ（px）需要滿足的基本約束條件。但要獲得高的噴管氣動性能，函數φ（px）還需要滿足如下條件：

在函數 φp（x）需要滿足的約束條件中，φ（p0）=0和 φ（p1）=1可稱為零階約束條件，（0）=0 和（1）=0可稱為1階約束條件。在滿足上述零階約束條件和1階約束條件的同時，x從0變化至1時，（x）先從0逐漸增大，然后又減小至0，即在x∈（0，1）區間內，φ（′x）只存在1個極大值（當然也可能存在多于1個極大值的情況，但本文不考慮這種情況）。因此，函數 φ（px）還需滿足如下2階約束條件：在x∈（0，1）區間內，方程）=0 只有 1 個根。

應該說，滿足上述要求的連續函數φp（x）的形式有無數種。選擇如下多項式函數來構造函數φp（x）

式中：c0、c1、c2、c3、……為待定系數。

根據0階和1階約束條件，可得到

根據式（26）、（28）可知，要同時滿足 0階和 1階約束條件，多項式函數的階次不能低于2次。將c0=c1=0 代入式（27）、（29），可進一步得到

由上面2式可知，2次多項式函數不能同時滿足式（30）、（31）。因此，同時滿足0階和1階約束條件的多項式函數階次不能低于3次。

根據式（30）、（31），結合 2階約束條件，得到同時滿足上述要求的3次和4次多項式函數。

3次多項式函數

4次多項式函數

式中：c4∈ -3,3[ ]且 c4≠0。若 c4=0，式（33）就變為如式（32）所示的3次多項式。

可以通過減少或增加約束條件構造出滿足不同二元收斂噴管設計要求的更多其他函數關系，構造方法與上述過程類似，詳細公式內容見文獻[15]。而本文所構造設計的上述多項式函數已具有較好的代表性和典型性，為進一步研究高性能二元收斂噴管橫截面控制參數沿程變化規律的選取打下基礎。

上面構造的典型3次和4次多項式函數曲線如圖3所示。

根據圖中曲線的變化規律特點，可以將上述多項式函數分為典型的3類：第1類是進、出口函數值變化緩急程度一致的函數關系（圖3中“Ⅲ型函數”），如：3 次函數，見式（32）；第 2 類是進口函數值變化較為劇烈、出口函數值變化較為緩慢的函數關系（圖3中“IV-2型函數”），如：4次函數φp（x）=6x2-8x3+3x4；第3類是進口函數值變化較為緩慢、出口函數值變化較為劇烈的函數關系（圖3中“IV-1型函數”），如：4次函數φp（x）=4x3-3x4。

在噴管進、出口截面面積和出口寬高比、噴管長度給定的前提下，構造二元收斂噴管型面的關鍵步驟是選擇橫截面控制參數及各參數的沿程變化規律，由進、出口截面參數值計算噴管沿程中間截面參數值，從而形成各中間截面。多種噴管方案詳細列表見文獻[15]。

圖3 4種典型多項式函數曲線

2 二元收斂噴管構型方案的數值計算分析

2.1 物理模型

以某混合排氣渦扇發動機為基準發動機，基于其工作過程參數和設計點推力性能要求，開展混合排氣二元收斂噴管設計研究。該發動機的原始噴管為固定式軸對稱收斂噴管，由于采用混合排氣方案，尾噴管同時起到混合室的作用，如圖4所示。噴管喉道面積（以面積比A8/A7表示）為A8/A7=0.477，噴管長度（以長徑比L/D7表示）為L/D7=0.465。對于混合排氣噴管，噴管進口截面位置也是1個關鍵幾何參數，本文以噴管進口截面到內涵出口截面之間的無量綱軸向距離N/D7表示，其中N為噴管進口截面至內涵出口截面之間的實際軸向距離。基準軸對稱收斂噴管的該進口截面位置參數N/D7=0.129。

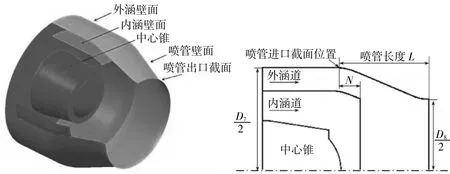
圖4 基準軸對稱收斂噴管幾何模型

基于基準軸對稱收斂噴管幾何尺寸設計AR=4（出口矩形的寬高比為4）二元收斂噴管的幾何模型。二元收斂噴管的喉道面積、噴管長度以及噴管進口截面位置均與基準軸對稱收斂噴管完全相同。將軸對稱收斂噴管修改設計為二元收斂噴管時，內涵通道和中心錐的幾何形狀和尺寸均保持原始設計不變。

圖5 二元收斂噴管構型方案

為對比不同噴管的氣動性能參數，分別對軸對稱收斂外涵噴管、縱向型線二元收斂外涵噴管以及超橢圓和圓角矩形二元收斂外涵噴管進行分析，如圖5所示。所有噴管均具有相同的進、出口截面面積和噴管長度（噴管進、出口截面面積比A8/A7=0.477，噴管長徑比L/D7=1.0），所有二元收斂噴管的出口寬高比均相同（AR=4）。其中，超橢圓二元收斂噴管方案AⅢaⅢbⅢ是指選擇長軸半徑a、短軸半徑b和面積A作為超橢圓截面的獨立控制參數，同時，控制參數的沿程變化選擇依據圖3中的3次多項式函數。圓角矩形二元收斂噴管方案AⅣ-2bⅣ-2rⅣ-2是指選擇矩形半高b、頂角圓弧半徑r和面積A作為圓角矩形截面的獨立控制參數，控制參數的沿程變化選擇依據圖3中的進口函數值變化較為劇烈、出口函數值變化較為緩慢的IV_2型函數。

2.2 數值計算結果

噴管流場計算模型分為內、外流場計算域，設噴管出口截面當量直徑為D8，外流域圓柱體直徑為10D8，長度為30D8。噴管進口總壓均設為1.5×105Pa，進口總溫設為500 K。外流場邊界設置為壓力出口，出口靜壓設為1.01325×105Pa，總溫為300 K。采用結構化網格對計算域進行空間離散，計算網格總數約180萬。

基準軸對稱收斂噴管和AR=4超橢圓二元收斂噴管的內、外流場流線分布如圖6、7所示。從圖中可見，基準軸對稱噴管的內涵氣流基本是由外涵氣流包圍著沿噴管軸向流出，2股氣流之間的摻混相對較弱。而二元收斂噴管的內涵氣流基本占據了噴管射流的中心區域，外涵氣流則被“擠”向靠近噴管出口“窄邊”的兩側，內、外涵氣流排出噴管后呈散射狀，摻混程度相對比較強烈。

圖6 基準軸對稱收斂噴管的內、外涵氣流流線

圖7 AR=4的二元收斂噴管內、外涵氣流流線計算結果

圖8 二元收斂噴管寬、窄邊對稱面

二元收斂噴管的寬邊對稱面和窄邊對稱面如圖8所示。在這2個對稱面上，基準軸對稱收斂噴管和AR=4超橢圓二元收斂噴管的射流速度分布特征如圖9所示。從圖中可見，軸對稱收斂噴管的射流具有軸對稱特征，在2個對稱面上的速度分布完全相同，而二元收斂噴管在2個對稱面上的速度分布存在顯著差別，在寬邊對稱面上的速度分布呈現出“多峰”形貌。

圖9 軸對稱和AR=4二元收斂噴管在寬、窄邊對稱面上的x方向速度分量等值線分布

軸對稱噴管、縱向型線二元噴管、超橢圓橫截面二元噴管以及圓角矩形橫截面二元噴管的流量系數和推力系數計算結果見表1。流量/推力的數值均是以基準軸對稱收斂噴管的流量/推力為單位進行無量綱化的結果，噴管的總推力Fg為

式中：m˙8為噴管出口質量流量；U為噴管出口軸向速度；p8和pa分別為噴管出口靜壓和出口環境壓力。

表1 不同噴管性能參數比較

從表中可見，縱向型線二元噴管的流量系數和推力系數明顯低于軸對稱噴管。超橢圓二元噴管AIV-2aIV-2bIV-2和圓角矩形二元噴管AIV-2aIV-2bIV-2均具有光順過渡的幾何外形，特別是采用了型面控制參數值在噴管出口附近平緩過渡的設計，使得噴管內流平穩，流動損失和非軸向射流動量損失明顯降低，因此，該2種二元噴管的流量系數和推力系數均已比較接近軸對稱噴管。

3 二元收斂噴管構型方案的試驗分析

混合排氣系統模擬試驗臺主要包括內涵燃氣發生系統、供油點火系統、外涵氣流系統和混合排氣系統4大部分。內涵燃氣發生系統主要由內涵風機和燃燒室組成，設計質量流量為1 kg/s。外涵氣流系統主要由外涵風機和穩壓腔組成，設計質量流量為1.2 kg/s。內、外涵氣流質量流量均在一定范圍內可調。供油點火系統主要由油箱、油泵、燃油控制臺及高能點火器等組成，為燃燒室提供燃油和點火控制。混合排氣系統主要由渦輪模擬件、中心錐、支板以及噴管等部件組成，較真實地模擬了某種渦扇發動機混合排氣系統。混合排氣系統可以換裝不同類型噴管。內涵氣流經燃燒室燃燒加熱后，可以使渦輪模擬件出口截面的氣流總溫達到800 K以上，與所模擬的真實發動機實際渦輪出口氣流總溫比較接近。內涵高溫燃氣氣流與外涵氣流在混合排氣噴管內混合并排入大氣。

對原軸對稱噴管和基于上述方法設計改型的出口寬高比分別為AR=2和AR=6的2種超橢圓截面二元收斂試驗噴管進行試驗研究。3種噴管總推力的數值計算和試驗結果對比見表2。二者之間存在一定差別，但由數值方法和試驗方法所得到的AR=2和AR=6的二元噴管的總推力與基準軸對稱噴管的相對差別均在3%以內。考慮到試驗件加工和試驗測量誤差，上述結果基本說明所設計的2種改型超橢圓截面二元噴管的總推力較接近于基準軸對稱噴管的，同時也驗證了數值計算方法的可靠性。

表2 3種噴管的總推力數值計算與試驗結果對比

4 結論

本文主要開展了高性能二元收斂噴管型面設計方法研究。對比分析表明：采用縱向型線簡單設計的二元噴管性能參數明顯低于軸對稱噴管的。而（超橢圓或圓角矩形）橫截面構型的二元噴管具有光順過渡的幾何外形，特別是采用型面控制參數值在噴管出口附近平緩過渡（選用“IV_2型函數”）的設計，使得噴管內流平穩，流動損失和非軸向射流動量損失明顯降低，其流量系數和推力系數均已較接近軸對稱噴管的。由此可見，基于超橢圓或圓角矩形橫截面構型二元噴管設計方法，通過選取合適的截面控制參數和沿程變化規律，均可設計出性能較高的二元收斂噴管。