科技創新驅動柳州制造業轉型升級的實證研究

張光明 魏鋒

[摘 要] 基于2003-2017年柳州市專利授權數和工業增加值數據，運用ADF檢驗、VAR模型脈沖響應函數分析、協整檢驗與誤差修正模型等方法對科技創新驅動柳州制造業轉型升級之間的關系進行了實證研究。結果表明，柳州市科技創新與制造業發展之間的長期穩定關系顯著，而科技創新對柳州制造業發展的短期影響關系不顯著，但長期影響持續有效，科技創新與柳州制造業發展之間的短期波動偏離二者長期關系的程度并不高。柳州市應發揮科技創新在制造業轉型發展中的引領和驅動作用，持續加大科技創新投入，加快科技創新成果轉化，積極引導各種創新要素聚集到企業，促進企業成為創新決策和創新成果轉化的主體，全面提升企業的自主創新能力，最終實現制造業的全面轉型升級。

[關鍵詞] 科技創新;制造業轉型升級;協整

[中圖分類號] F204[文獻標識碼] A[文章編號] 1009-6043（2019）11-0054-02

科技創新與制造業轉型升級之間的關系一直是眾多學者的研究熱點。李勝文等（2016）利用1998-2010年制造業企業經驗數據進行實證分析，發現科技創新對產業升級具有顯著貢獻[1]。楊智峰等（2014）通過建立投入產出模型分析各產業部門產出增長發現，科技進步推動了2002-2007年的產業結構優化升級[2]。王維（2012）認為中國工業轉型升級的制約因素之一就在于科技創新效益不高[3]。李杰（2009）在研究產業結構演進的一般規律后發現，技術密集化和信息化將是制造業發展的方向及其結構演進的核心動力[4]。以上研究大多基于國民經濟產業角度，而且主要針對發達地區，缺乏對區域經濟特別是欠發達地區科技創新與制造業發展關系的深入研究。本文以中國西部工業城市——廣西柳州市為研究對象，對其科技創新與制造業發展關系進行了實證研究，以期能為該地區科技創新驅動制造業的轉型升級提供理論參考和政策建議。

一、指標選擇與數據處理

（一）指標選擇

現代制造業科技創新成果的主要表現形式為專利，考慮數據的可得性，因此選用專利授權數（文中記為ZL）作為科技創新水平的衡量指標。由于制造業屬于工業的主要產業門類，考慮數據的可得性，因此選用工業增加值（文中記為GY）作為制造業發展水平的衡量指標。

（二）數據來源和處理

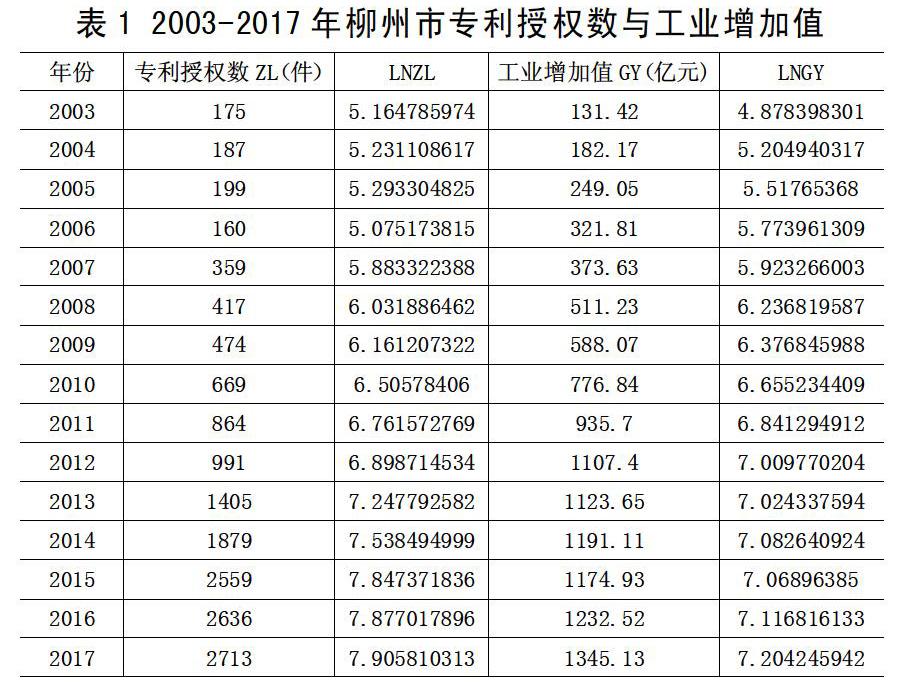
本文選擇2003-2017年柳州市專利授權數與工業增加值數據（原始數據均來源于各年度《柳州市國民經濟與社會發展統計公報》），為消除原始數據序列可能存在的異方差性，同時不改變兩個指標之間的長期關系，本文對專利授權數ZL與工業增加值GY兩個指標原始數據均作了自然對數變換處理，處理后的數據序列分別記為LNZL與LNGY，所有數據見表1。

二、科技創新驅動柳州制造業發展關系的實證分析

（一）變量的平穩性檢驗

經典回歸分析理論要求所使用的時間序列數據滿足平穩性特征，否則對不平穩時間序列數據直接使用回歸分析會產生“偽回歸”的不合理現象，計量經濟學中解決該問題的辦法是對數據進行平穩性檢驗，ADF檢驗就是一種常用的數據平穩性檢驗方法，本文使用Eviews7.0對LNZL與LNGY分別進行了ADF檢驗，檢驗結果見表2。

由表2可知，LNZL與LNGY的ADF統計量絕對值小于其5%臨界值的絕對值，同時相伴概率p也均大于5%，說明兩個數據序列在顯著性水平為5%時均不平穩，但是兩個差分數據序列D（LNZL）與D（LNGY）在顯著性水平為5%時均為平穩序列，由此證明LNZL與LNGY兩個均屬于一階單整數據序列，二者之間可能會存在協整關系。

（二）VAR模型及脈沖響應函數分析

1.VAR模型

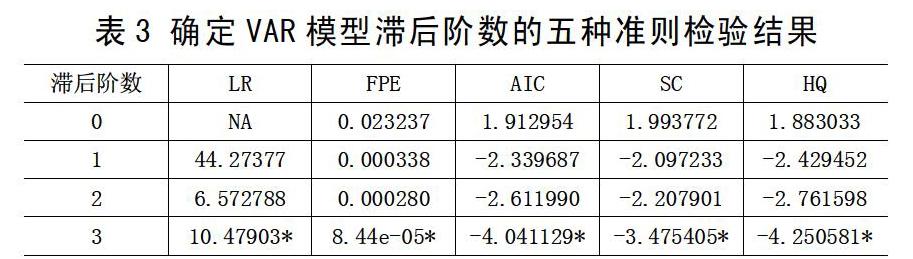
VAR是一種常用的計量經濟模型，它是用模型中的當期變量對所有變量的若干滯后變量進行回歸，一般用來估計多個內生變量間的動態關系。VAR建模無需任何關于變量的約束條件，但需確定變量的滯后階數，一般通過LR、FPE、AIC、SC與HQ五種檢驗準則進行比較來選擇最優滯后階數，本文使用Eviews7.0分別得到五種準則的檢驗結果，并在各準則最優滯后階數對應的檢驗值右上角標注星號，所得結果如表3所示，顯然五種準則確定的最優滯后階數均為3，因此本文可得一個VAR（3）模型，同時可由VAR估計結果知該模型所有特征根均落在單位圓內，表明該VAR模型結構是穩定的，可以進行脈沖響應函數分析。

2.脈沖響應函數分析

脈沖響應函數描述了VAR模型中每個內生變量的一個標準差沖擊對自身及其他內生變量所造成的影響。在VAR模型中第i個內生變量的一個沖擊不僅直接影響其本身，而且通過VAR的動態結構傳遞給其他的內生變量，脈沖響應函數刻畫的就是這種影響的軌跡，從而顯示任意一個變量的擾動是如何通過模型影響所有其他變量，最終又反饋到本身的過程[5]。本文使用Eviews7.0得到了LNGY的脈沖響應表（見表4）。

（三）協整檢驗

協整檢驗是常用來處理非平穩變量數據之間是否存在長期均衡關系的計量分析方法，關于兩變量之間的協整檢驗常用方法是EG兩步法，具體如下[6]：

第一步，根據兩個變量數據進行OLS回歸，本文以LNZL為解釋變量，以LNGY為被解釋變量，運用Eviews7.0進行了回歸分析，結果見表5。由表5可知，回歸方程擬合優度較高（可決系數R2=0.870416），自變量LNZL對應回歸系數（0.689125）的相伴概率接近0說明該回歸系數很顯著，回歸方程的F值（87.32090）很高同時相伴概率接近0說明整個回歸方程效果顯著[6]。

第二步，對所得回歸方程的殘差序列進行平穩性檢驗，如果殘差序列屬于平穩序列，第一步所建立的回歸方程是有效的，表明變量間的協整關系成立。本文運用Eviews7.0對該殘差序列進行了ADF檢驗，結果見表6。由表6可知，殘差序列的ADF檢驗統計量值小于5%顯著性水平下的臨界值，表明在5%顯著性水平下殘差序列是平穩序列，這說明LNZL和LNGY之間存在協整關系[6]，即科技創新對柳州制造業轉型發展的影響關系是長期穩定的，這與前文脈沖響應函數分析得出的結論是一致的。

（四）誤差修正模型

協整回歸方程反映的是變量之間的長期均衡關系，這種長期關系實際上是在短期關系的不斷累計中形成的。根據Granger表述定理，如果兩個變量之間是協整的，則它們之間的短期非均衡關系一定可以通過一個誤差修正模型（ECM）來描述[7]。本文借助Eviews7.0建立了LNGY與LNZL的以下誤差修正模型：

Δ（LNGYt）=0.177815-0.053051Δ（LNZLt）-0.11177ecmt-1

其中誤差修正項ecmt-1=LNGYt-1-0.689125LNZLt-1

-1.918557，它反映了變量在短期波動中偏離其長期均衡關系的程度。誤差修正模型反映了前文中協整方程因變量LNGYt的短期波動Δ（LNGYt）受兩個因素影響：一是自變量LNZLt的短期波動Δ（LNZLt）帶來的影響，二是誤差修正項ecmt-1的影響。誤差修正項ecmt-1的系數-0.11177為負，這種負向修正機制可以這樣去解釋：當LNGYt-1大于其長期均衡值時ecmt-1為正，則Δ（LNGYt）減小，使得LNGY對其長期均衡值的偏離減弱;當LNGYt-1小于其長期均衡值時ecmt-1為負，則Δ（LNGYt）增大，使得LNGY對其長期均衡值的偏離增強，無論出現哪種情況LNGY與LNZL之間的長期均衡關系均得以維持。誤差修正系數-0.11177反映了LNGY與LNZL之間的短期波動中有大約11%會在下一年獲得修正[7]，這說明科技創新與柳州制造業轉型發展之間的短期波動偏離二者長期均衡關系的程度并不高，此結論與前文脈沖響應函數分析不謀而合。

三、結論與建議

本文運用ADF檢驗、VAR模型脈沖響應函數分析、協整檢驗與誤差修正模型等方法對科技創新驅動柳州制造業轉型升級之間的關系進行了實證研究。其中，ADF檢驗發現柳州市專利授權數和工業增加值均為不平穩序列，但二者的一階差分序列均為平穩序列;VAR模型脈沖響應函數分析表明科技創新對柳州制造業轉型發展的短期影響不穩定，但長期影響是持續有效的;協整檢驗進一步證明柳州市科技創新與制造業發展之間存在顯著的長期均衡關系，科技創新對柳州制造業轉型發展的促進作用是長期穩定的;誤差修正模型顯示科技創新與柳州制造業轉型發展之間的短期波動偏離二者長期均衡關系的程度并不高。因此，柳州市應始終堅持科技創新在制造業轉型發展中的引領和驅動作用，持續加大科技創新投入，加快科技創新成果轉化力度，積極引導各種創新要素聚集到企業，促進企業成為創新決策和創新成果轉化的主體，全面提升企業的自主創新能力，最終實現制造業的全面轉型升級。

[參考文獻]

[1]李勝文，楊學儒，檀宏斌.技術創新、技術創業和產業升級——基于技術創新和技術創業交互效應的視角[J].經濟問題探索，2016（1）：111-117.

[2]楊智峰，陳霜華，汪偉.中國產業結構變化的動因分析——基于投入產出模型的實證研究[J].財經研究，2014（9）：38-49.

[3]王維.全球視角下的中國工業轉型升級制約因素分析[J].亞太經濟，2012（4）：66-70.

[4]李杰.產業結構演進的一般規律及國際經驗比較[J].經濟問題，2009（6）：31-34.

[5]張光明.廣西物流業與制造業聯動關系的實證研究[J].物流技術，2014（5）：201-220.

[6]張光明.廣西區域物流與區域經濟互動關系的實證分析[J].物流技術，2014（6）：121-140.

[7]張光明，廖志高.廣西港口物流與對外貿易關系的實證研究[J].物流技術，2015（6）：93-95.

[8]高鐵梅.計量經濟分析方法與建模[M].北京：清華大學出版社，2009.

[責任編輯：史樸]