基于Bezier曲線的特殊螺紋密封面參數化設計*

張 穎，練章華

(1.四川輕化工大學 過程裝備與控制工程四川省高校重點實驗室，四川 自貢 643000；2.西南石油大學 油氣藏地質及開發工程國家重點實驗室，四川 成都 610500)

0 引言

隨著我國對天然氣資源需求量的不斷增加，天然氣勘探開發逐漸向深層、超深層發展，井下環境日趨復雜。以塔里木油田為例[1]，近5 a油管失效123井次，其中管端接箍開裂、油管斷裂占比達43%，造成重大經濟損失。管端螺紋的密封性能對井筒完整性和安全性的要求越來越高，常規的API系列螺紋接頭已不能滿足要求，而特殊螺紋接頭在深井、超深氣井取得了廣泛的關注和應用。

Murtagian等[2]通過物模試驗和數值模擬方法研究特殊螺紋密封性能的影響因素，得出特殊螺紋泄漏預測的數學模型和螺紋密封評價準則；Xie等[3-4]建立特殊螺紋金屬對金屬密封結構的試驗模型，研究了密封面長度、油管尺寸、表面粗糙度、螺紋密封脂等因素對密封性能的影響；高連新等[5-6]利用有限元技術和全尺寸試驗相結合的方法，研究特殊螺紋接頭密封設計的方法，指出密封結構形式的選擇與密封面過盈量的確定是特殊螺紋密封設計的關鍵因素；王建東等[7]采用有限元方法，針對錐面/錐面和球面/錐面2種不同密封結構形式，計算分析了不同載荷工況下螺紋密封面上的接觸應力，得出不同密封結構組合下密封能力隨載荷的變化規律；張永強等[8]基于圓螺紋設計并加工了1種氣密封螺紋結構，接箍中間增加了彈性密封圈，依靠彈性密封圈與套管螺紋的過盈配合實現密封，該氣密封螺紋可在鄂爾多斯盆地低壓氣井、CO2埋存與驅油項目中使用，并能大幅度節約套管成本；張穎等[9-10]建立了特殊螺紋密封面接觸應力松弛力學數學模型，以及在微觀尺度下建立氣體通過金屬密封間隙泄漏速率的理論模型，詳細分析討論特殊螺紋的泄漏機制及影響規律；許紅林等[11-13]針對特殊螺紋球面對錐面密封結構，建立了考慮密封面作用扭矩的氣密封壓力計算理論模型，研究了球面半徑、錐面錐度等參數對螺紋氣密封性能的影響規律。

綜上所述，本文提出油套管特殊螺紋密封結構應具有以下特征：曲面對錐面密封，密封接觸壓力主要源自徑向楔緊力，密封接觸壓力應基本上不受端面軸向扭矩臺階壓緊力影響。Bezier曲線具有良好的形狀控制能力，在幾何造型設計方面有強大的優勢，特別是在汽車、航天航空等領域得到了廣泛的運用[14-15]。本文在Bezier曲線理論的基礎上，提出1套特殊螺紋扣球面對錐面密封結構參數設計的方法，并基于此方法對特殊螺紋密封接頭進行優化設計。

1 特殊螺紋密封面結構設計

1.1 Bezier曲線基本理論

1971年法國Renault公司的工程師Bezier提出1種獨創的曲線曲面造型方法[16]，即由控制多邊形來設計曲線。

Bezier曲線的表達式如下：

(1)

式中：Bi,n(t)為 Bernstein基函數；Pi為Bezier曲線的控制頂點。

式(1)為n階Bezier曲線，將Pi(i=0,1,…,n)順序首尾連接，從Po到Pn所形成的折線稱為控制多邊形或者Bezier多邊形[17]。其中控制點P0和Pn是Bezier曲線的起始點和終點，其余的控制點通常不在Bezier曲線上。

式(1)中，當n=1時，則表示線性Bezier曲線方程為：

B1(t)=P0+(P1-P0)t=(1-t)P0+tP1,t∈[0,1]

(2)

式(2)等同于線性插值，如圖1所示。

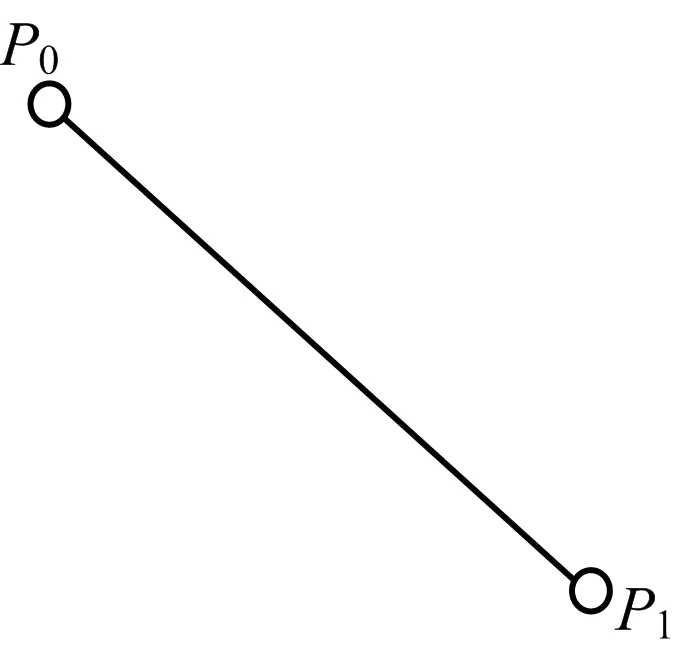
圖1 線性Bezier曲線Fig.1 Linear Bezier curve

當n=2時，二階Bezier曲線的表達式如下，

B2(t)=(1-t)2P0+2t(1-t)P1+t2P2,t∈[0,1]

(3)

二階Bezier曲線由3點構成，其原理是是曲線去逼近控制點P0，P1，P2所構成的三角形，這種曲線能夠表達具有一定弧度的形狀，如圖2所示。

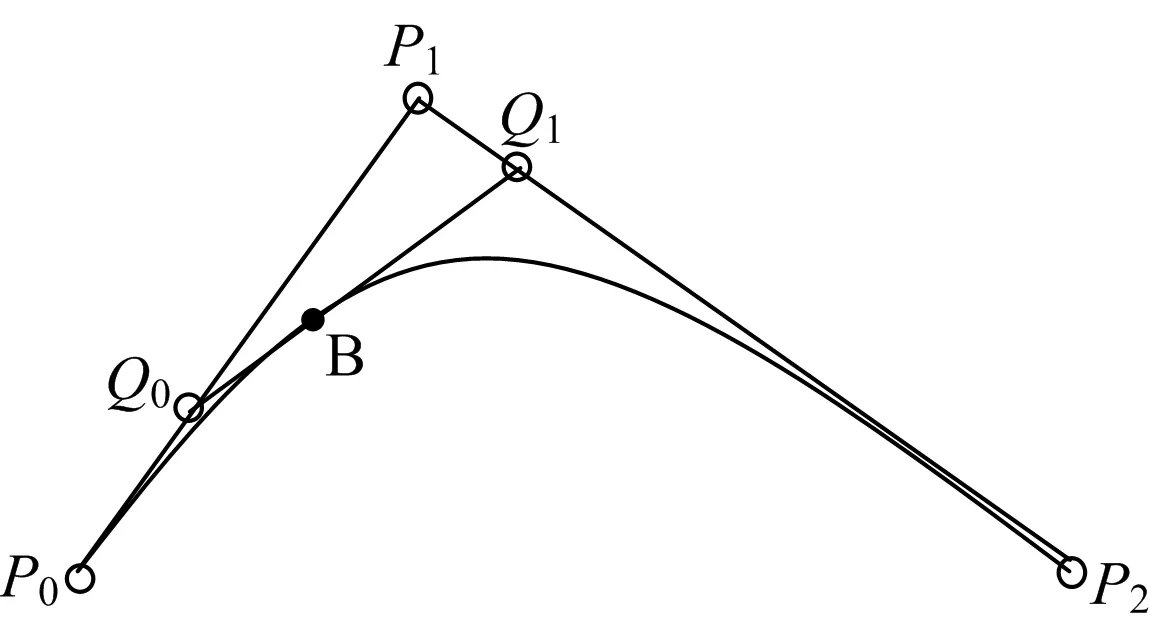
圖2 二階Bezier曲線Fig.2 Second-order Bezier curve

圖2中，P0，P1，P2分別是二階Bezier曲線的控制頂點。Q0在直線段P0P1上變化，從P0移動至P1，Q0的軌跡線描述了一階線性Bezier曲線；Q1在直線段P1P2上變化，從P1移動至P2，同樣，Q1的軌跡線描述了一階線性Bezier曲線；B點是線段Q0Q1的線性插值點，隨Q0和Q1點位置的變化而不斷變化，最終形成的路徑如圖2中曲線所示，該曲線就是二階Bezier曲線。其中，線段P0P1和P1P2與二階Bezier曲線保持相切。

當n=3時，三階Bezier曲線的表達式如下：

(4)

三階Bezier曲線方程表示了P0，P1，P2和P44個點在平面或在三維空間中定義了三階Bezier曲線。如圖3所示。圖3中Q0，Q1和Q2分別在線段P0P1，P1P2和P2P3上移動，其各自的運動軌跡描述了一階線性Bezier曲線。R0和R1分別為線段Q0Q1和Q1Q2的線性插值點，其各自的運動軌跡線描述了二階Bezier曲線。B點是線段R0R1所形成線性插值點，其運動軌跡則為三階Bezier曲線，如圖3中曲線所示。其中，線段P0P1和P2P3與三階Bezier曲線保持相切。

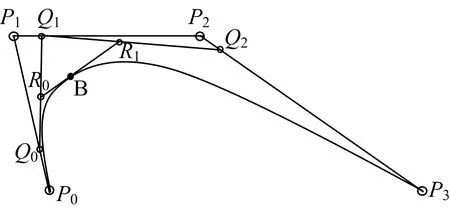
圖3 三階Bezier曲線Fig.3 Third-order Bezier curve

1.2 特殊螺紋密封面結構設計

在工程實踐中，常用2次或3次Bezier曲線來滿足曲率的連續。針對特殊螺紋扣曲面對錐面密封結構，為了增大特殊螺紋扣密封面接觸應力，提高密封接觸能，并減小密封接頭的塑形變形區域面積，提出采用三階Bezier曲線作為公接頭密封面的曲面方程。基于Bezier曲線公接頭密封面結構設計如圖4所示。

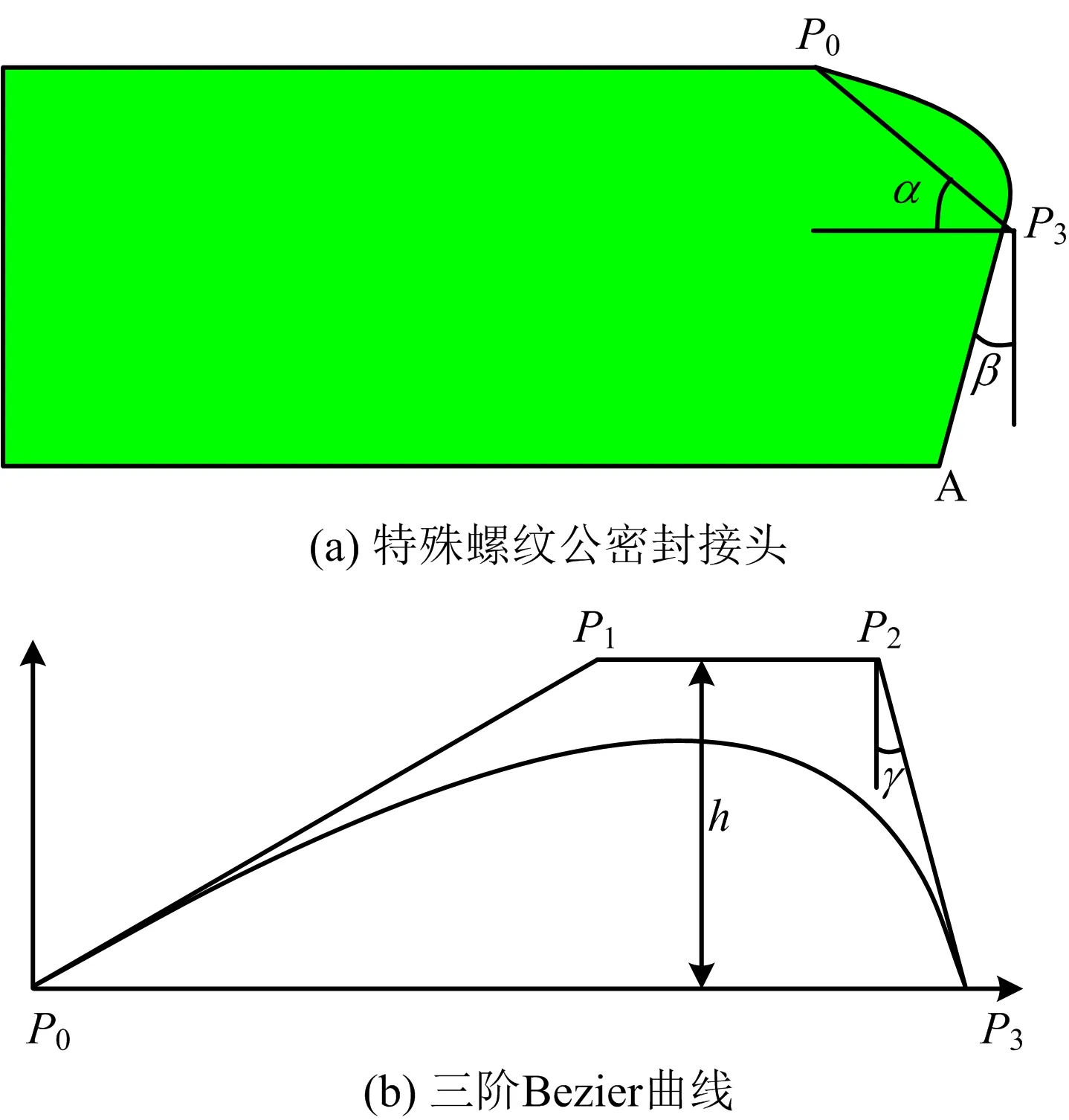
圖4 基于Bezier曲線公接頭密封面結構設計Fig.4 Structural design of sealing surface for pin joint based on Bezier curve

根據三階Bezier曲線方程，首先需要確定4個控制點P0，P1，P2和P3的坐標參數，如圖4(b)。結合Bezier曲線起點和終點特性，可以確定圖中P0為Bezier曲線的起始坐標點位置，P3為Bezier曲線的終點坐標位置。且規定線段P0P3的水平方向夾角α與母接頭密封面內錐角相同。AP3為公接頭鼻端止推臺肩面，線段AP3與垂直方向夾角為β。

圖4(b)為公接頭密封面Bezier曲線設計圖。根據Bezier理論，控制點P1和P2為自由設計點，由于特殊螺扣止推臺肩幾何角度和母密封接頭幾何關系的約束，設計過程中，要求Bezier曲線與公接頭止推臺階面AP3相切，即線段P3P2為線段AP3的延長線。且線段P1P2長度為線段P0P3長度的0.3倍。根據平面幾何知識，圖4(b)中，控制點P2的夾角γ的表達式為：

γ=α-β

(5)

假設控制點P0位置坐標為(0，0)，線段P0P3長為l，控制點P1，P2到線段P0P3的高度為h。則得出4個控制點P0，P1，P2和P3的位置坐標分別為(x0，y0)，(x1，y1)，(x2，y2)和(x3，y3)。

根據圖4(b)三階Bezier曲線控制點幾何關系，由解析幾何可得：

將式(3)三階Bezier曲線參數方程展開，可得：

(6)

將控制點P0，P1，P2和P3的坐標帶入式(6)即可得到公接頭Bezier曲線密封面方程。

Bezier曲線密封面與相同尺寸參數下橢圓曲線密封面的對比如圖5所示。其中，Bezier曲線控制參數，l=5 mm，h=1 mm，α=40°，β=15°。從圖5中可以看出，Bezier曲線相較與橢圓曲線曲面，在密封接觸位置，其曲線凸出更為尖銳，而在非密封接觸區域，曲線較為平緩。

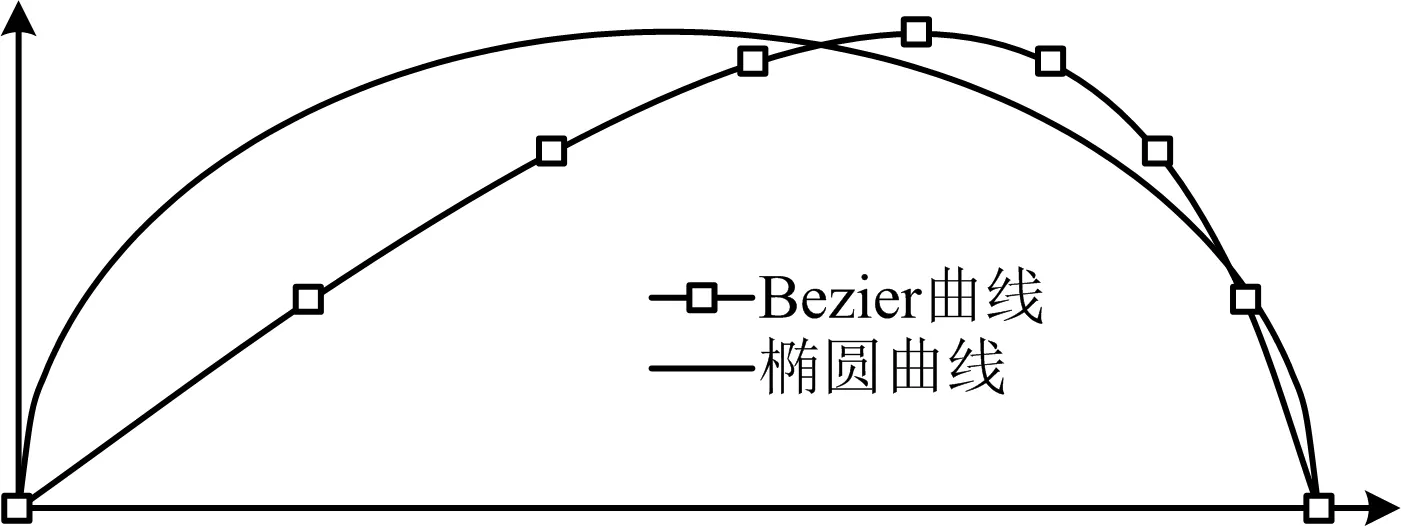
圖5 Bezier曲線密封面與橢圓曲線密封面Fig.5 Sealing surfaces of Bezier curve and elliptic curve

2 密封面結構數值仿真研究

2.1 數值仿真模擬

根據Bezier曲線密封面結構設計參數，建立了特殊螺紋扣密封接頭的有限元力學模型，如圖6所示。由圖6可知，公接頭密封面采用Bezier曲線密封面，母接頭密封面采用錐形密封面，其密封形式屬于球面對錐面密封。螺紋接頭所用材料為P110T鋼級，系各向同性材料，彈性模量為2.10×105MPa，泊松比為0.29，材料的屈服強度為805 MPa。采用127 mm油管，密封接頭尺寸基本參數見表1。

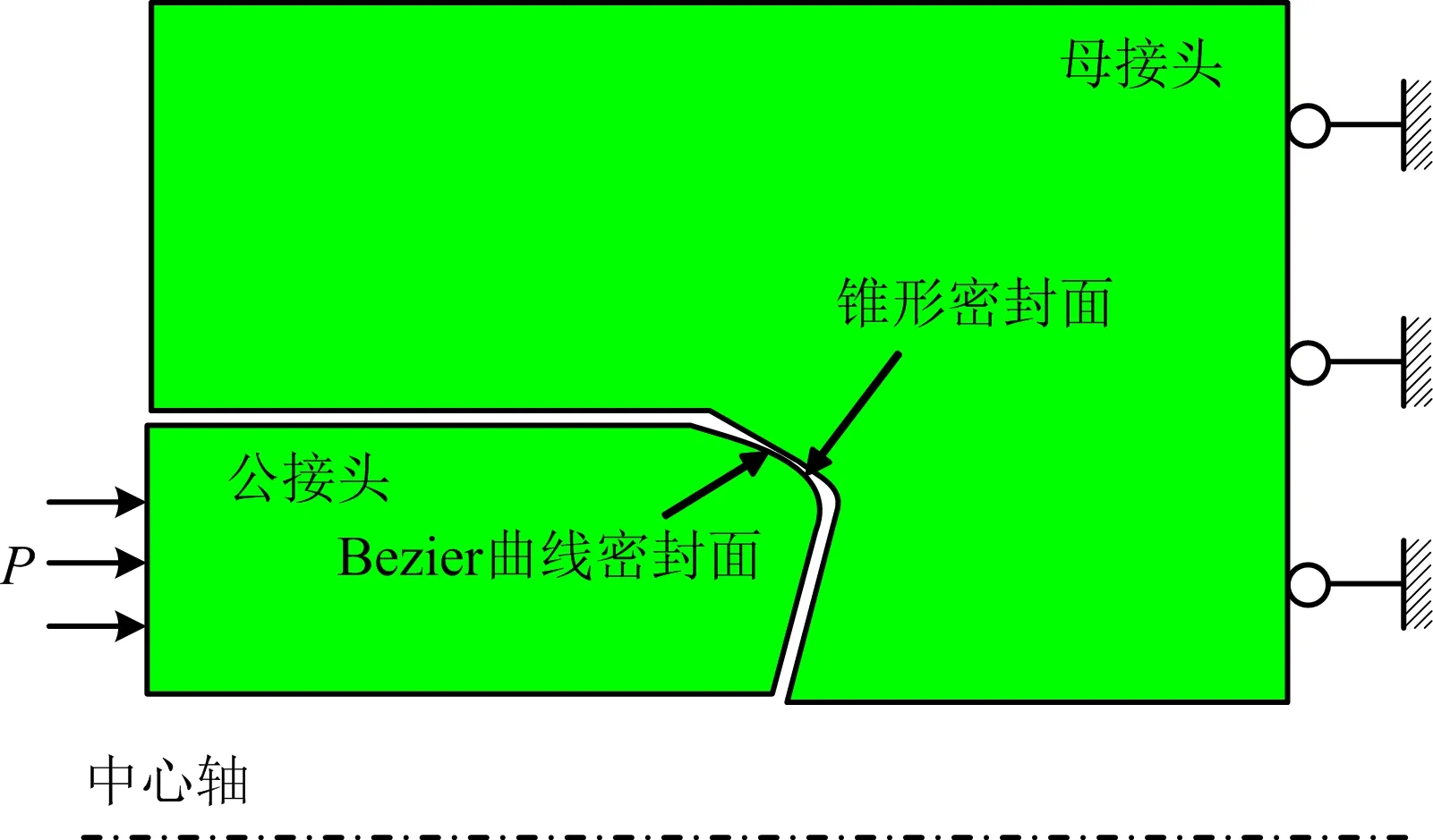
圖6 基于Bezier曲線設計的特殊螺紋扣密封接頭有限元力學模型Fig.6 Finite element mechanical model for sealing joint of premium connection based on Bezier curve design

表1 基于Bezier曲線設計的特殊螺紋扣密封接頭基本參數Table 1 Basic parameters for sealing joint of premium connection based on Bezier curve design mm

基于Bezier曲線設計的特殊螺紋扣密封接頭Von-Mises應力的分布云圖如圖7所示，由圖7可知，密封接頭整體處于彈性變形狀態，而在密封面附近出現了塑形變形，其最大Von-Mises應力達到827.4 MPa，說明該密封面已經進入塑形屈服階段。

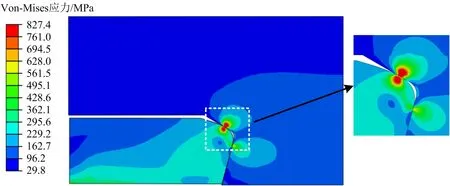
圖7 基于Bezier曲線設計的特殊螺紋扣密封接頭Von-Mises應力分布Fig.7 Distribution of Von-Mises stress in sealing joint of premium connection based on Bezier curve design

基于Bezier曲線設計的特殊螺紋扣密封接頭密封面上接觸應力分布見圖8所示。由圖8可知，經過優化設計的特殊螺紋接頭密封面最大接觸壓力達2 060 MPa，密封接觸長度為0.6 mm。該密封結構符合金屬對金屬密封塑形填充要求，在較小的密封接觸范圍內，產生較大的接觸壓力。同時，根據金屬密封接觸能理論，阻止氣體通過金屬對金屬密封結構的流動阻力可由密封接觸強度fs表征，它定義為密封接觸應力在有效密封長度上的積分值[11]。

(7)

式中：fs為密封接觸強度，MPa·mm；L為有效密封接觸長度，mm。PsN為密封面上接觸應力，MPa。

通過式(7)可以計算出基于Bezier曲線設計的特殊螺紋扣密封接頭的密封接觸能為821 MPa·mm。

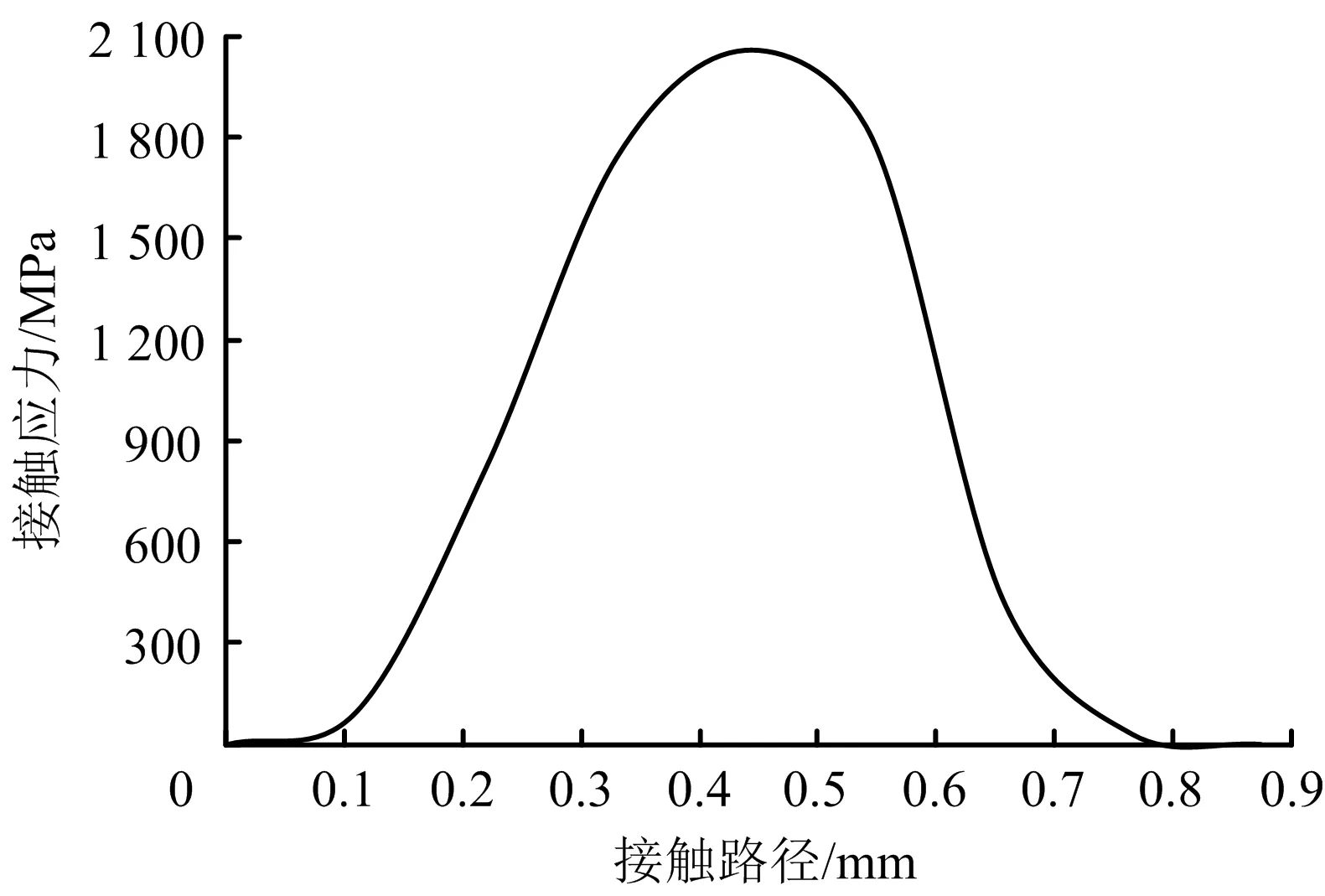
圖8 基于Bezier曲線設計的特殊螺紋扣密封接頭密封面應力分布Fig.8 Stress distribution on sealing surface for sealing joint of premium connection based on Bezier curve design

2.2 對比分析

將相同尺寸結構的橢圓密封面特殊螺紋扣密封接頭與基于Bezier曲線設計的特殊螺紋扣密封接頭進行對比分析。其接觸面上的Von-Mises應力分布云圖以及接觸面上的接觸應力分布曲線分別如圖9～10所示。由圖9可知，基于Bezier曲線方程設計的特殊螺紋接頭，密封面周圍進入塑形區域面積明顯減小。塑形區域的減小，可以減小油管接頭出現的疲勞破壞，管體裂紋擴展發生的概率。由圖10可知，雖然Bezier曲線密封面的密封接觸能821 MPa·mm比橢圓曲線密封面的密封接觸能905 MPa·mm降低10%，但其密封面的最大接觸應力提高了30%，密封接頭塑形區域面積減小了40%。因此，該新型密封結構有利于提高特殊螺紋接頭的抗疲勞性能，預防特殊螺紋接頭應力腐蝕斷裂。

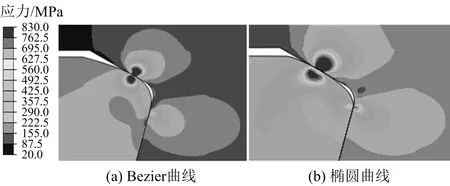
圖9 密封接觸面Von-Mises應力分布Fig.9 Nephogram of Von-Mises stress on sealing contact surface

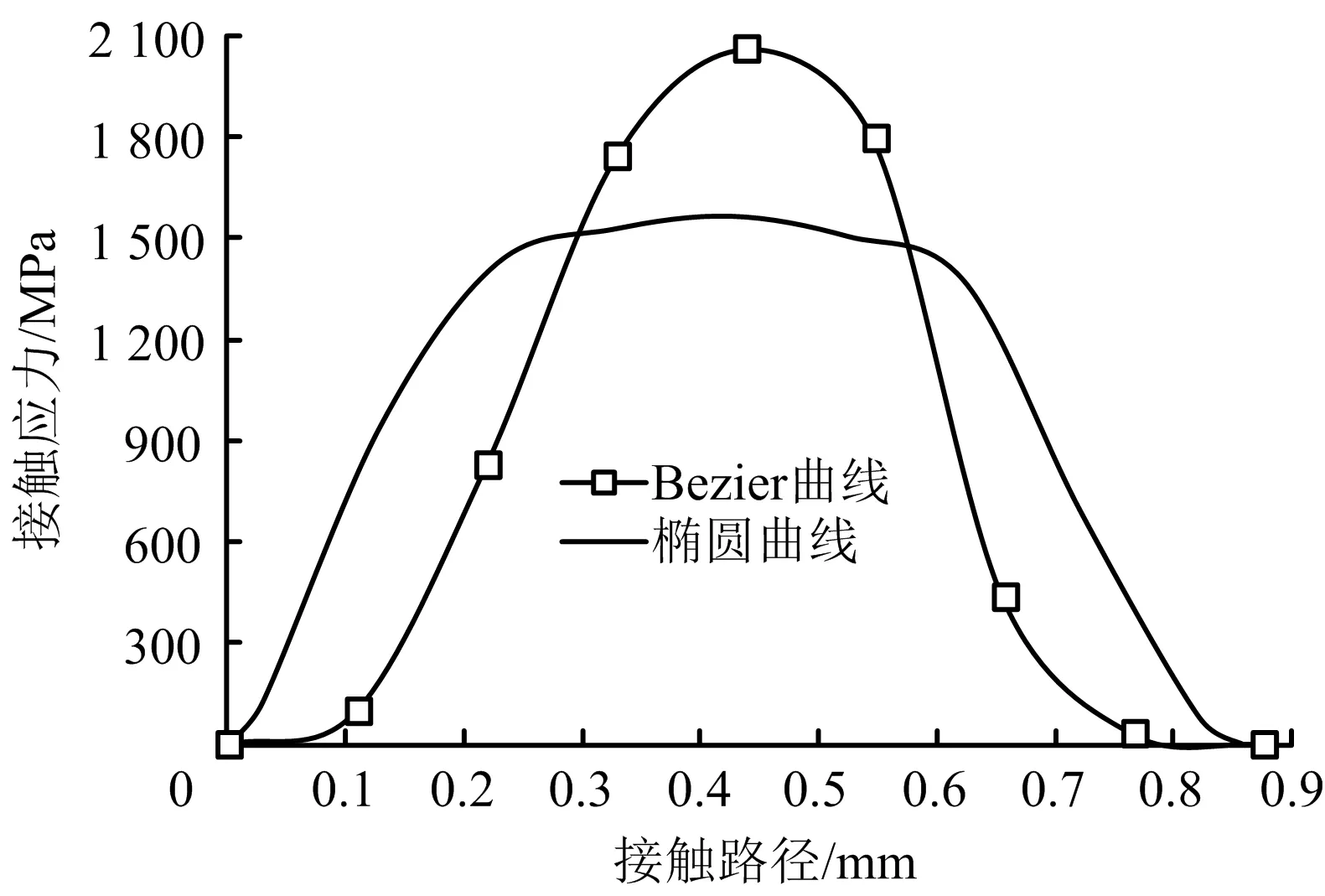
圖10 特殊螺紋扣密封接頭密封面接觸應力分布對比Fig.10 Comparison of contact stress distribution on sealing surface for sealing joint of premium connection

3 結論

1)基于三階Bezier曲線理論，建立了特殊螺紋密封面球面對錐面密封結構參數化設計模型，通過數值模擬手段，對特殊螺紋密封性能進行系統研究。針對特殊螺紋球面對錐面密封結構，利用Bezier曲線在幾何造型的巨大優勢，可為特殊螺紋密封面球面設計提供依據。

2)基于Bezier曲線設計的新型特殊螺紋接頭密封結構，該螺紋接頭提高了密封面接觸壓力，改善了螺紋接頭密封面塑形區域面積，該新型密封結構有利于提高特殊螺紋接頭的抗疲勞性能，預防特殊螺紋接頭應力腐蝕斷裂。

(3)基于Bezier曲線設計的特殊螺紋扣密封接頭密封面具有良好的力學性能，可以為深井、超深井油管柱螺紋接頭的密封設計提供理論依據。