剖分-點聯圖和剖分-邊聯圖的Kirchhoff指標

馬婷妍，王維忠

(蘭州交通大學 數理學院， 甘肅 蘭州 730030)

1993年，Klein等[1]提出了圖的電阻距離的概念。將圖G的每條邊用一個固定電阻代替，則對應得到電網絡N，圖G的頂點i和j之間的電阻距離rij等于電網絡N中節點i和j之間的有效電阻，其求解過程遵循基爾霍夫法則和歐姆定律。Kirchhoff指標Kf(G)定義為圖G的所有頂點對之間的電阻距離之和。1996年，Gutman[2]和Zhu[3]等分別證明了圖的Kirchhoff指標與其拉普拉斯特征值之間的如下關系：

Kirchhoff指標是分子結構描述符，是一個重要的拓撲指標，關于它的研究已有很多成果[4-13]，其中文獻[13]研究了R-點聯和R-邊聯圖的Kirchhoff指標。受此啟發，本文考慮剖分-點聯和剖分-邊聯圖的Kirchhoff指標。

本文僅考慮簡單的無向圖。設圖G=(V,E)的頂點集和邊集分別為V={1,2,…,n}和E={e1,e2,…,em}，并設DG=diag(d1,d2,…,dn)是圖G的度對角矩陣，其中di(1≤i≤n)為頂點i的度。圖G的鄰接矩陣AG=(aij)n×n定義如下：若頂點i和j相鄰，則aij=1；否則aij=0。圖G的Laplacian矩陣LG=DG-AG，其特征值為μ1≥μ2≥…≥μn=0(LG特征值的多重集就稱作圖G的Laplacian譜)。設BG=(bij)n×m是圖G的點-邊關聯矩陣，若頂點i與邊ej關聯，則bij=1；否則bij=0。

1 預備知識

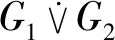
為了方便，設Jn×n表示元素均為1的n階矩陣，1表示元素均為1的列向量。

圖1 G1=G2=P2時的剖分圖、剖分-點聯圖及剖分-邊聯圖

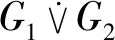
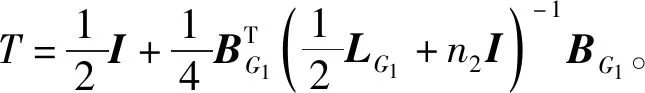
引理2[14]設G1為n1個頂點m1條邊的d-正則圖，G2為n2階圖，則G1和G2的剖分-邊聯圖G1G2的Laplacian矩陣的{1}-可逆矩陣為

其中l(G1)為G1的線圖。

引理3[15]設G為n階連通圖，則Kf(G)=ntr(L(1)(G))-1TL(1)(G)1。

2 主要結果

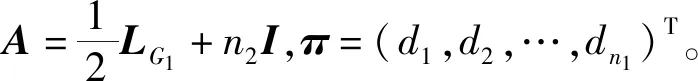
證明由引理1可得

(1)

tr(A-1DG1)+tr(A-1AG1)，

(2)

(3)

同理可得

(4)

將式(2)—(4)帶入式(1)可得

(5)

由引理1同時可得

(6)

由于BG11=π，所以

(7)

又因為

(8)

(9)

(10)

同樣地，(LG2+n1I)-11=n11表明

(11)

將式(7)—(11)代入式(6)可得

(12)

結合式(5)和式(12)，由引理3可得定理2.1。

在定理2.1中，若G1為正則圖，則可得推論2.2。

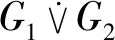
其次，當G1為正則圖時，得到如下關于剖分-邊聯圖G1G2的Kirchhoff指標計算公式。……