概率統計經典題突破

編者的話：“經典題突破方法”欄目里的例、習題選自名校模擬題或三年高考真題，推出本欄目的主要目的是讓同學們更好地領悟數學解題思想方法，通過多解多變培養同學們多思多想的好習慣。學會解題反思，無疑是同學們學習的一條捷徑，愿同學們不斷地在反思中進步，在反思中收獲！本期特約河南省項城市第一高級中學的張慧敏、韓維崢兩位老師為同學們解讀相關知識。愿同學們通過閱讀，能從中感悟知識的結構與拓展，把握第19題、第20題的命題特點與趨勢。

高中數學內容中的概率統計是大學統計學的基礎，起著承上啟下的作用。高考對概率統計內容的考查主要是古典概型、幾何概型、統計的基礎知識與方法。大題偏向于對統計知識、數據分析處理能力的考查。

一、經典題突破

例1 為了監控某種零件的一條生產線的生產過程，檢驗員每天從該生產線上隨機抽取16個零件，并測量其尺寸（單位：cm）。根據長期生產經驗，可以認為這條生產線正常狀態下生產的零件的尺寸服從正態分布N（μ，σ2）。

（1）假設生產狀態正常，記X表示一天內抽取的16個零件中其尺寸在（μ-3σ，μ+3σ）之外的零件數，求P（X≥1）及X的數學期望。

（2）-天內抽檢的零件中.如果出現了尺寸在（μ- 3σ，μ+3σ）之外的零件，就認為這條生產線在這一天的生產過程可能出現了異常情況，需對當天的生產過程進行檢查。

①試說明上述監控生產過程的方法的合理性。

②下面是檢驗員在一天內抽取的16個零件的尺寸：

9.95 10.1 9.96 9.96 10.0 9.92 9.98 10.010.2 9.91 10.13 10.0 9.22 10.0 10.0 9.95

2.考點定位與考查意圖。

本題考查了統計學在生產實踐中的應用，根據抽樣統計，進行樣本數據分析，反映了利用科學的方法搜集、整理、分析和提供關于社會經濟現象、某些特定事物發展規律的數學思想，著重考查數據處理能力和運算求解能力，以及應用所學知識分析問題、解決問題的能力。考查正態分布、獨立重復試驗、對立事件、隨機變量的概率與數學期望。概率統計重視實際應用是考查的重點，學生可以從解題過程中認識到統計與概率知識在生產與生活中所起的作用。通過對問題的解決，給學生展示了問題的提出、模型的建立、數據的整理與分析、統計與概率知識的應用，從而形成應用數學知識指導社會實踐的意識，提高學生的綜合實踐能力。

3.錯誤原因。

概率統計中基本概念較多，理解不到位，文字閱讀量偏大，數據的信息點多，計算量偏大，對于學生的運算能力要求較高，概率統計解答題的實際背景新穎，對閱讀理解、推理分析、數據運算的要求較高，因此難度較大。

4.復習建議。

重視考綱考點的變化，高考全國卷中的概率統計解答題一直都比較重視數學應用，側重于統計思想、數據分析與處理、結合生活實際的決策性問題，突出應用意識。

重視基本概念的梳理，概率與統計中的基本概念眾多，在復習備考過程中引導學生回歸教材，對教材中的基本概念進行梳理。

重視基本原理的研究，高考全國卷中的概率統計解答題重點考查統計與概率的基礎知識、基本原理和基本方法，所以我們要加強對概率論與數理統計內容的學習與研究。

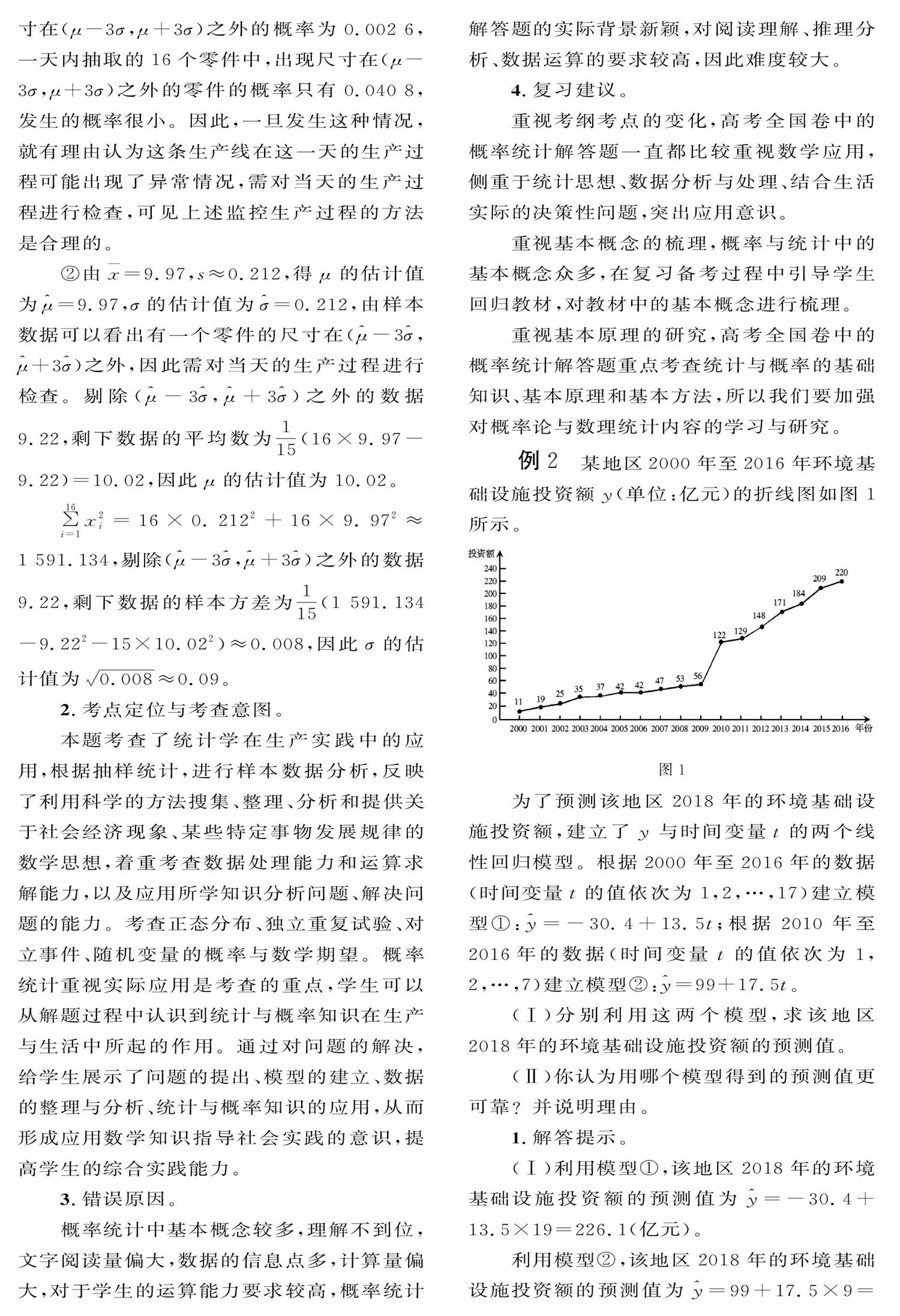
例2某地區2000年至2016年環境基礎設施投資額y（單位：億元）的折線圖如圖1所示。

為了預測該地區2018年的環境基礎設施投資額，建立了y與時間變量t的兩個線性回歸模型。根據2000年至2016年的數據（時間變量t的值依次為1，2，…，17）建立模型①：y=-30.4+13. 5t;根據2010年至2016年的數據（時間變量t的值依次為1，2，…，7）建立模型②：y=99+17. 5t。

（I）分別利用這兩個模型，求該地區2018年的環境基礎設施投資額的預測值。

（Ⅱ）你認為用哪個模型得到的預測值更可靠？并說明理由。

1.解答提示。

（工）利用模型①，該地區2018年的環境基礎設施投資額的預測值為y=一 30.4+13.5×19=226.1（億元）。

利用模型②，該地區2018年的環境基礎設施投資額的預測值為y=一99+17.5×9=256.5（億元）。

（Ⅱ）利用模型②得到的預測值更可靠。

理由如下：

（1）從折線圖可以看出，2000年至2016年的數據對應的點沒有隨機散布在直線v-- 30.4十13.5t的上方和下方。這說明利用2000年至2016年的數據建立的線性模型①不能很好地描述環境基礎設施投資額的變化趨勢。2010年相對2009年的環境基礎設施投資額有明顯增加，2010年至2016年的數據對應的點位于一條直線的附近，這說明從2010年開始環境基礎設施投資額的變化規律呈線性增長趨勢，利用2010年至2016年的數據建立的線性模型y=99+17.5t可以較好地描述2010年以后的環境基礎設施投資額的變化趨勢，因此，利用模型②得到的預測值更可靠。

（2）從計算結果看，相對于2016年的環境基礎設施投資額220億元，由模型①得到的預測值226.1億元的增幅明顯偏低，而利用模型②得到的預測值的增幅比較合理。說明利用模型②得到的預測值更可靠。

2.考點定位與考查意圖。

通過建立數學模型，解決實際問題是高考考試要求的重要內容。特別是伴隨著大數據時代的到來，人們常常需要對網絡、文本、聲音、圖像等大量信息進行數字化處理，使數學模型的研究領域與應用領域得到極大拓展，特別是隨著統計與概率知識在中學數學內容的增加，為學生的數學建模提供了知識儲備和解題工具。在對其考查時，可以從模型建立、檢驗模型等方面設置問題。在對數學建模考查時，更為注重根據題干中的精確數據構建數學模型，強調用數學知識、思想方法解決數學問題的能力，淡化對數據的分析和處理，試題以環境投資為背景，首先給出了環境基礎設施投資額的折線圖，旨在考查學生通過折線圖進行數據分析的能力。該題重點考查數學模型建立的選擇，試題的設計有利于培養學生的數學應用意識，學生領會到統計與概率的思想方法在現實生活中有著廣泛的應用，形成自覺應用數學知識指導社會實踐的意識，提高學生的綜合實踐能力。數學模型是應用數學知識解決實際問題的一種有效的工具。

3.錯誤原因。

不重視數學原理和數學應用，數學應用意識比較淡漠，不注重與實際的結合，難以對現實問題中的有用數據進行處理與模型構建。沒有計算的耐心和準確度。

4.復習建議。

教材是學習數學基礎知識、形成基本技能的“藍本”，是高考試題的重要知識載體。縱觀新課程卷中的概率統計試題，大多數試題源于教材，特別是客觀題都是從課本上的練習題或習題改編的，即使是綜合題.也是由教材例、習題的組合、加工和拓展而成，充分表現出教材的基礎作用。復習階段必須按《教學大綱》和《考試說明》對本部分內容的要求，以課本的例、習題為素材，深入淺出、舉一反三地加以類比、延伸和拓展，在“變式”上下功夫，力求對教材內容融會貫通。

重視數學思想方法的滲透，數學思想方法作為數學的精髓，歷來是高考數學考查的重中之重。它蘊含在數學知識發生、發展和應用的過程中。在概率統計的內容中蘊含著豐富的數學思想方法，概率統計為人們處理現實數據信息，分析、把握隨機事件，提供了強有力的工具（計算隨機事件發生的概率、求隨機變量的數學期望與方差），也更加豐富、完善了中學數學思想方法，進一步拓寬了知識的應用空間。

重視概率統計的應用功能，由于新課程強調數學教育的基礎性、現實性、大眾性，重視素質教育與高考的兼容性，概率統計在社會現實中具有很高的應用價值。在復習中要關注生活背景、社會現實、經濟建設、科技發展等各個方面，并從中提煉出具有社會價值的數學應用背景。應注意培養學生善于從普通語言中捕捉信息，將普通語言轉化為數學語言的能力，使學生能以數學語言為工具進行數學思維與數學交流。

二、跟蹤練習

例3 某城市為了解游客人數的變化規律，提高旅游服務質量，收集并整理了2014年1月至2016年12月期間月接待游客量（單位：萬人）的數據，繪制了圖2所示的折線圖。根據該折線圖，下列結論錯誤的是（ ）。

A.月接待游客逐月增加

B.年接待游客量逐年增加

C.各年的月接待游客量高峰期大致在7、8月

D.各年1月至6月的月接待游客量相對于7月至12月，波動性更小，變化比較平穩

解析：由折線圖可知，8月份以后的月接待游客量減少，A錯誤;年接待游客量逐年增加，B正確;各年的月接待游客量高峰期大致在7、8月份，C正確;各年1月至6月的月接待游客量波動性小，變化比較平穩，D正確。故選A。

例5某工廠的某種產品成箱包裝，每箱200件，每一箱產品在交付用戶之前要對產品進行檢驗，如檢驗出不合格品，則更換為合格品。檢驗時，先從這箱產品中任取20件進行檢驗，再根據檢驗結果決定是否對余下的所有產品進行檢驗。設每件產品為不合格品的概率都為p（O

（1）記20件產品中恰有2件不合格品的概率為f（p），求f（p）的最大值點P0。

（2）現對一箱產品檢驗了20件，結果恰有2件不合格品，以（1）中確定的p。作為p的值。已知每件產品的檢驗費用為2元，若有不合格品進入用戶手中，則工廠要對每件不合格品支付25元的賠償費用。

①若不對該箱余下的產品進行檢驗，這一箱產品的檢驗費用與賠償費用的和記為X，求E（X）;

②以檢驗費用與賠償費用和的期望值為決策依據，是否該對這箱余下的所有產品進行檢驗？

分析：本題以企業在銷售過程中的成本控制問題為背景，著眼于“最小化成本”的決策問題，綜合考查了概率統計知識。