船舶管理中基于負載平衡的并行 FP-growth算法研究

尚 弘，徐平平，姚 湘

(1.無錫太湖學院 江蘇省物聯網應用技術重點建設實驗室，江蘇 無錫 214064；2.東南大學 信息科學與工程學院，江蘇 南京 210096)

0 引 言

近年來，物聯網技術發展迅猛，各行業的數據都呈現井噴趨勢，大數據已經成為規模龐大的船舶運營管理中不可或缺的一部分。將數據技術應用到船舶管理領域，不僅限于將采集的數據信息化、可視化，更重要的是通過深度挖掘技術，將數據中所蘊含的信息應用于智能化船舶安全管理、船舶資源管理、物流貿易等領域，發揮大數據和人工智能技術在促進經濟發展、提高航運貿易量及船舶運能中的積極作用，從而推動整個行業快速前行。

1993年，R.Agrawal等提出了關聯規則的概念及其模型，目前最經典的是1994年R.Agrawal等提出的Apriori算法和2000年Han等提出的FP-growth算法[1]。胡曉軒將改進型Apriori算法應用于船舶安全管理中，通過對生產中的考核指標進行挖掘分析，發現指標間的高度關聯關系，分析和事故的相關性，并將其作為預警因子，提前預防安全事故的發生[2]。孫斌采用改進的多維Apriori算法，挖掘人為失誤導致船舶碰撞事故的頻繁因素組合，并對該人為失誤致因進行分析[3]，以此來提高船舶航行的安全系數。顧洵瑜等提出利用FP-growth算法，采用分治方式，不產生候選項集[4]，直接挖掘船舶滯留原因間的潛在關聯，分析滯留原因，進行針對性檢查，提高安全檢查效率。

相對Apriori算法而言，FP-growth算法的效率明顯提升，但當數據量快速增長時，該算法構建的頻繁模式樹（Frequent Pattern tree，FP-tree）在橫向和縱向的維度上會越來越大，不僅容易造成FP-tree構建過程中出錯，而且也會導致在頻繁項集的遞歸挖掘過程中花費更多時間，造成挖掘效率低下。由于Spark采用了彈性分布式架構的編程接口，ZHANG Feng等提出了基于Spark框架的分布式頻繁項集挖掘方法[5]，該方法能很好地適用于大數據挖掘。章志剛等提出并行挖掘算法FPPM，該算法首先在各分計算節點上挖掘頻繁項集，然后將各頻繁項集進行合并得到全部的頻繁項集，最后對不滿足最小支持度要求的頻繁項集再次計算支持度[6]。

為了進一步提高船舶管理中數據挖掘效率，本文提出基于負載平衡的并行FP-growth數據挖掘算法，將原來在一個分區節點對整個FP樹的挖掘轉換為在多個分區節點上對分組FP樹的挖掘，不僅簡化了頻繁項集的挖掘過程，減少了計算量，而且通過負載均衡技術，使多分區節點并行運算，壓縮了挖掘時間。實驗表明，該算法能夠較好地提高船舶管理中數據挖掘的效率，并具有較好的可擴展性。

1 FP-growth算法描述

FP-growth算法將數據映射到FP-tree上，通過遞歸的方法，挖掘出全部頻繁項集。FP-growth算法的基本過程分為2個步驟[7]：

步驟1構建FP樹

1）遍歷數據集，統計各元素出現的次數，創建頭指針表；

2）將小于最小支持度的項從頭指針表中剔除；

3）再次對數據集遍歷，過濾和重排序每個元素項，并創建根節點為NULL的樹fp_t。

步驟2挖掘頻繁項集

1）從頭指針表中最下面的頻繁元素項開始，根據相同類型元素鏈表的指針，向上遍歷fp_t，得到其相應的條件模式基α；

2）基于步驟1的數據，構建FP樹，并將小于最小支持度的元素項剔除掉，從而挖掘出頻繁項集；

3）迭代重復步驟1和步驟2，挖掘獲取所有的頻繁項集β。

2 基于負載平衡的并行FP-growth算法研究

2.1 關聯規則相關概念

關聯規則是用于表示元素項之間關聯關系的一種形式，對于2個互斥的元素項X和Y，可以用X?Y來表示X出現將導致Y出現。可用支持度和置信度來實現對關聯規則的度量。

設I為m個互斥元素項組成的集合。

定義1對于關聯規則R：X?Y，其中X?I，Y?I。規則R的的支持度（Support）是數據集中X和Y同時出現的記錄數與所有記錄數之比，即

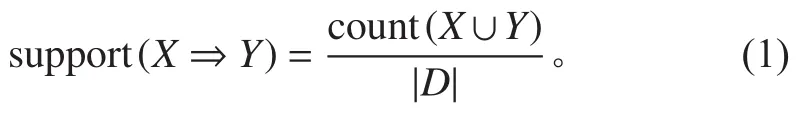
定義2對于關聯規則R：X?Y，其中X?I，Y?I。規則R的置信度（Confidence）是數據集中X和Y同時出現的記錄數與只有X出現的記錄數之比，即

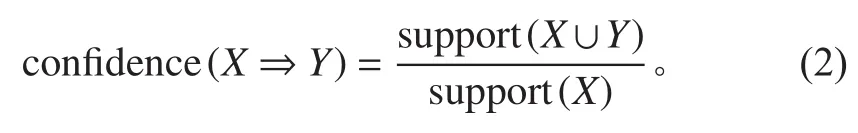
定義3最小支持度和最小置信度，最小支持度（Minimum Support，minsup）從統計分析的角度表示元素項的最低重要性；最小置信度（Minimum Confidence，minconf）從統計分析的角度表示關聯規則的最低可靠性。

關聯規則的挖掘實際上就是從所有滿足最小支持度的項集中挖掘滿足最小置信度的規則的過程，也就是挖掘強關聯規則的過程[8]。

2.2 算法基本思想

本文提出的基于負載平衡的并行FP-growth數據挖掘算法基于以下結論：

1）頻繁項集的子集是頻繁的。

2）設元素i?I，support（i）≥ minsup，k-FItemS（i）為所有包含元素i的k項頻繁項集，則k-FItemS（i）的并集為項目集I的頻繁項集。

2.3 算法項目樹構建

在對海量的船舶管理數據進行關聯挖掘時，構建的FP-Tree在橫向和縱向維度上會變的非常龐大，挖掘效率也會隨之而降低。為解決此問題，本文提出一種基于時間片段和TID的項目樹構建方法。對任意滿足i?I的元素，系統按照一定的規則和順序分配一個唯一的TID，對任意T?I，首先，按照TID（i）對T中的元素進行排序，將T存入數據庫的同時，按照系統事先設置的時間片段值，構建項目樹，為壓縮樹存儲空間，相同前綴的路徑可以共用，通過鏈接，相同元素被連接成為一個鏈表。在構建項目樹的同時，為項目樹構建頭表節點，頭表中元素按照TID的升序排列，數據結構為ItemName：TID：count：Node-Links，其中，Node-Links指向項目樹中與它同名的節點，如圖1所示。

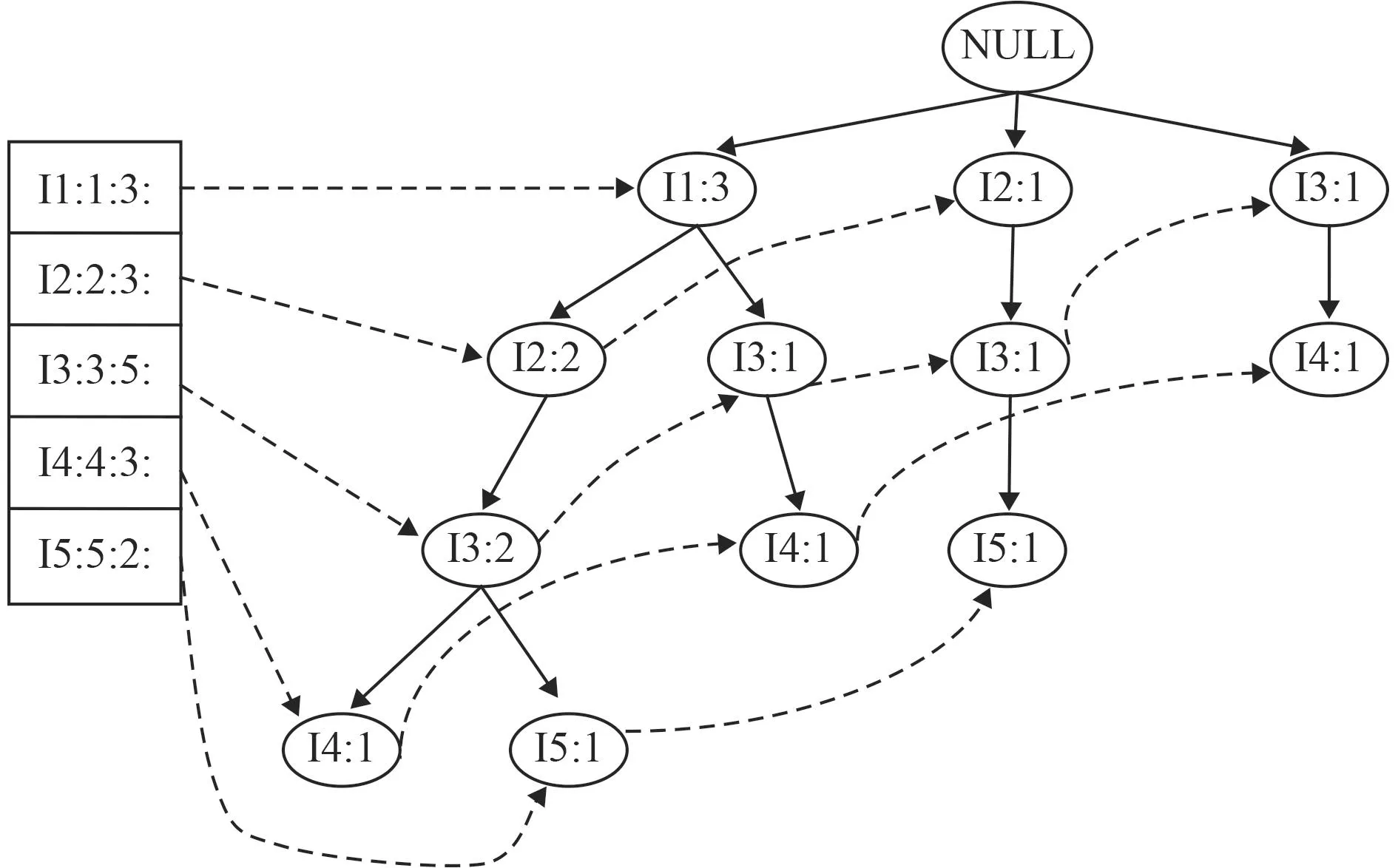
圖1 項目樹Fig.1 Project tree

2.4 算法實現

BPFP-growth算法主要分為4個核心部分：

1）計算數據庫項目集中的1-項頻繁項集。

為了挖掘1-項頻繁項集，首先根據項目樹集的頭表htab值建立矩陣模型，通過式（3）計算1-項集支持度：

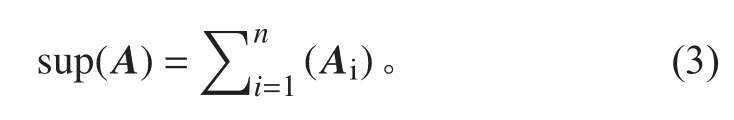
遍歷過濾掉小于最小支持度閾值的元素項，挖掘獲取所有的1-項頻繁項集α。

2）掃描項目樹，產生并行分組子項，結果存儲在單獨的數據庫文件中。

并行分組是該算法中最核心的一環，根據算法的基本思想，對上述挖掘獲取的1-項頻繁項集α中的元素項集{a1，a2，···，an}，循環掃描項目樹 ptree，通過對數據項進行過濾、剪枝，構建頭結點為ai的分組子項集pns_t。

3）計算負載因子，根據負載因子完成并行分組，結果存儲在分布式文件中。

并行挖掘中的分組是非常重要的環節，因為在并行挖掘中，各分區節點中最后一個完成挖掘任務節點的結束時間決定了整個系統最終的結束時間，因此，如何分配任務，使各分區節點的任務相對平衡，分組策略就顯得非常關鍵。

在構建分組子項樹時，從根節點到葉子節點的支持度逐步降低，搜索路徑逐步減少，且分組中節點數量也不盡相同。本文綜合考慮節點數量和路徑長度，賦予不同的權重wi。若同一層搜索路徑內的節點數量為bi，可通過下式計算分組子項的負載因子：

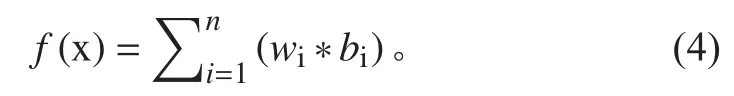
循環遍歷分組子項集pns_t，構建生成對應的FP樹分組子項集fp_pns_t，通過式（4）計算分組子項集fp_pns_t中每個分組子項的負載因子，根據負載因子完成負載平衡分組gr_fp_t。

4）挖掘頻繁項集。

在每個計算節點上，并行讀取分布式文件，循環遍歷挖掘負載平衡分組gr_fp_t中的各子項集，生成分組頻繁項集，匯總各計算節點挖掘結果求得全局頻繁項集β。

3 實驗與結果分析

為了驗證本文提出的BPFP-growth算法在船舶管理數據挖掘中的有效性和可擴展性，構建3個節點組成的并行計算平臺。隨機抽取10 000條數據作為實驗數據集，實驗測試結果如下：

1）BPFP-growth算法與FP-growth算法性能比較

在最小支持度為10的情況下，分別選取1 000條、2 000 條、3 000 條、······、10 000 條的數據集，將 BPFP-growth算法在2個并行分區計算節點和3個并行分區計算節點上的運算性能與傳統的FP-growth算法進行對比測試，實驗結果如圖2所示。

從圖2可以看出，不論采用何種挖掘算法，當數據集增大時，挖掘的數據量增大，頻繁項集增多，遞歸挖掘所需要的資源和運算次數增多，導致挖掘的復雜度增大，最終使整個系統的挖掘時間延長。

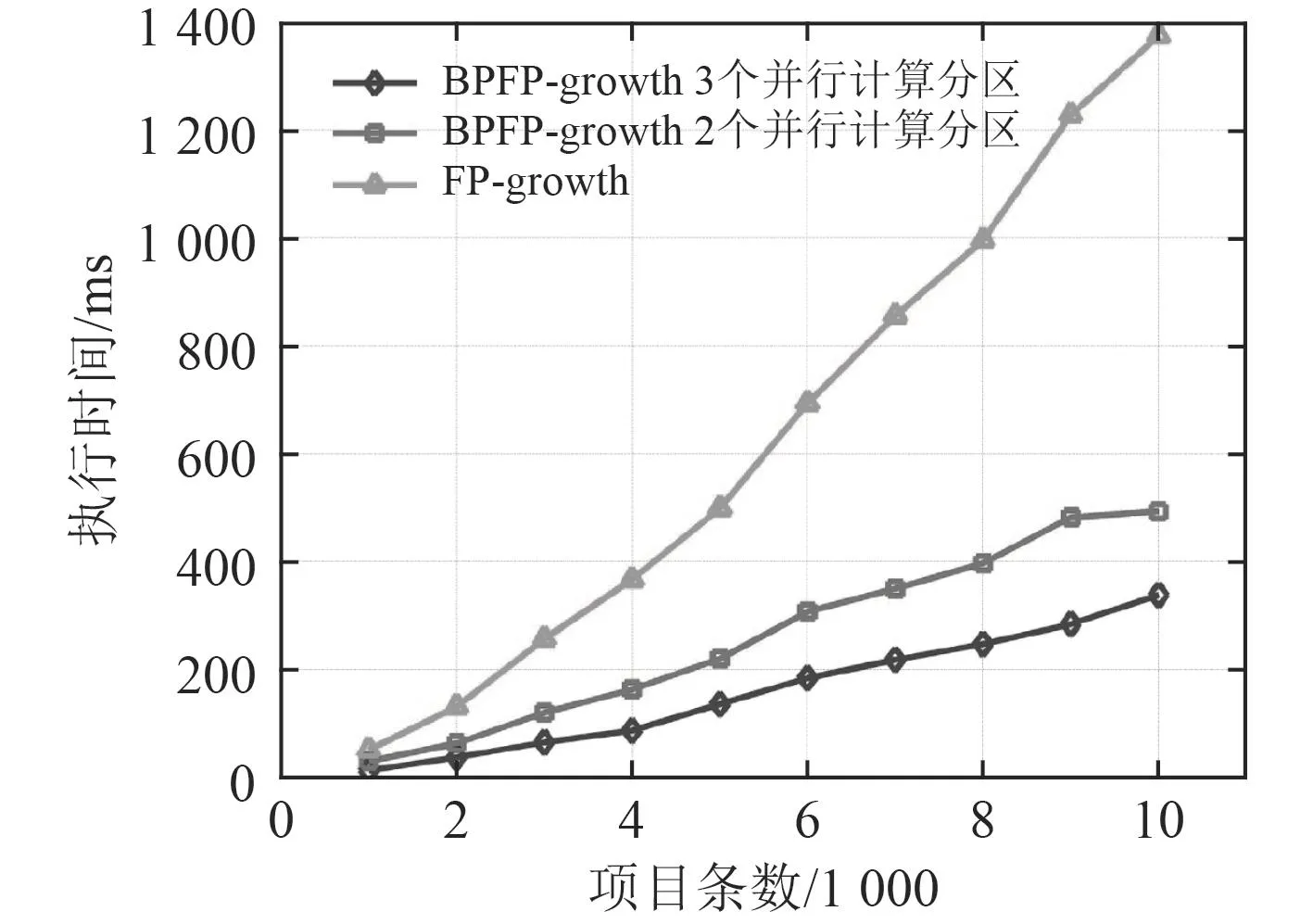
圖2 BPFP-growth算法與FP-growth算法性能比較Fig.2 Performance comparison between BPFP-growth algorithm and FP-growth algorithm

另外，從圖2還可以看出，當并行分區計算節點增多時，數據被平衡分布到更多的計算節點，所以，對于單個計算節點而言，所要處理的數據量減少，相應所花費的挖掘時間也縮短，呈現線性下降趨勢。因此該算法具有較好的可擴展性。

2）BPFP-growth算法自身性能分析

當最小支持度為5，10，20的情況下，分別選取1 000 條、2 000 條、3 000 條、······、10 000 條的數據集在3個并行分區計算節點上進行對比測試，實驗結果如圖3所示。

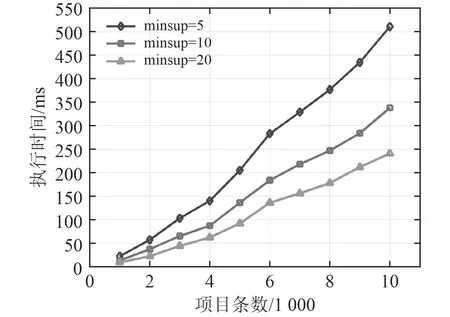
圖3 BPFP-growth算法自身性能分析Fig.3 Performance analysis of BPFP-growth algorithms

可以看出，當選定的最小支持度增大時，被剔除掉的項目數將增多，這時剩余項目數減少，挖掘的數據集規模降低，使得遞歸挖掘所需要的資源和運算的次數減少，計算復雜度降低，縮短了整個數據挖掘的時間。

4 結 語

本文提出的BPFP-growth算法基于鏡像重構技術對數據集進行切割，然后通過負載因子完成切割數據的并行分組與挖掘。實驗結果表明，該算法在面向船舶管理大數據的頻繁項集挖掘時，具有較好的可并行性和可伸縮性，可以有效挖掘出高度相關的頻繁項集，從而能夠利用該頻繁項集完成船舶運營中的安全管理、事故原因分析等，大大降低事故發生率，提高資源的配置效率。