有航速縱向連接多聯浮體頻域特性分析

魏 梟，陳徐均，苗玉基,2，黃 恒

(1.陸軍工程大學 野戰工程學院，江蘇 南京 210007；2.中國船舶科學研究中心，江蘇 無錫 214082)

0 引 言

海上浮式棧橋橋節（橋段）在從深水到淺水浮運過程中會遭遇不同方向的來浪，為提高拖航效率可能會把幾個浮體單元縱向串聯在一起拖航，串聯在一起的多個浮體在多大的航速可以安全通行就顯得尤為重要。對不同水深、不同浪向以及不同航速下縱向連接多聯浮體的水動力特性研究是上述安全性分析的基礎，是一種特殊連接方式的多浮體水動力分析，國內外相關研究包括多體動力學分析、多浮體水動力分析和航行浮體的水動力特性分析等。多體動力學分析方面，Michel G.和Daniel J.R.[1]提出了一種將彈性體變形的自由度公式與線性振動的脈沖基描述相結合的柔性多體動力學方法；Marcel E.和Jurnan S.[2]提出了一種新的柔性多體系統動力學方程；Lee H.W.等[3]提出了基于有限元的適用于多體系統的系泊線模型。多浮體水動力分析方面，Zhao H.等[4]采用隨機波頻域法對兩模塊浮式平臺進行了動力分析；Yang S.H.等[5]提出了一種浮動多體的波能轉換器，求解浮式多體系統的幅頻響應；韋斯俊等[6]對浮體間相互作用對水動力性能的影響進行了研究；張周康和洪亮[7]對浮體系統進行了不同海況的預測和設計優化。航行浮體的水動力特性方面，苗玉基等[8]分析了帶航速三體渡駁在波浪中航行時的水動力特性，以及航速和環境因素對其幅值響應算子的影響；陳振緯等[9]應用三維勢流理論的水動力軟件AQWA分析了一種新型工程船舶在波浪中的運動響應；李鴻等[10]利用AQWA軟件對不同海洋環境下的系泊多浮體耦合系統進行了全耦合時域分析,得到浮體的運動響應和纜繩受力情況。

本文基于三維勢流理論，利用水動力商業軟件Ansys-Aqwa對有航速縱向連接多聯浮體的水動力特性進行數值計算，主要對縱向連接多聯浮體在不同水深條件、不同浪向角和不同航速下的運動幅值響應算子RAOs（Response amplitude operators, RAOs）隨波浪頻率的關系進行分析。本研究可為浮體的拖航、運輸提供一定的借鑒和指導，并為后續的時域分析奠定基礎。

1 計算原理及方法

假定有航速的縱向連接多聯浮體所處的流場為無黏無旋不可壓縮的理想流體。因此，流場的運動可以采用三維勢流理論來描述。流場的邊界由物面邊界，流體自由表面，海底邊界面和無窮遠處柱面構成，有航速的多聯浮式結構周圍流場的速度勢由定常速度勢和非定常速度勢組成，可表示為[11]：

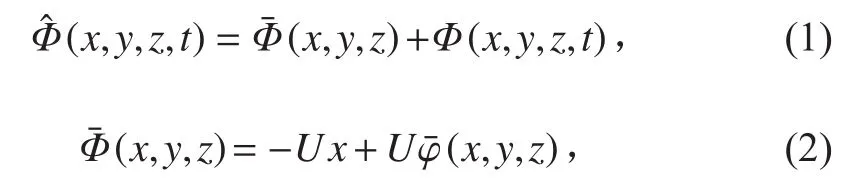
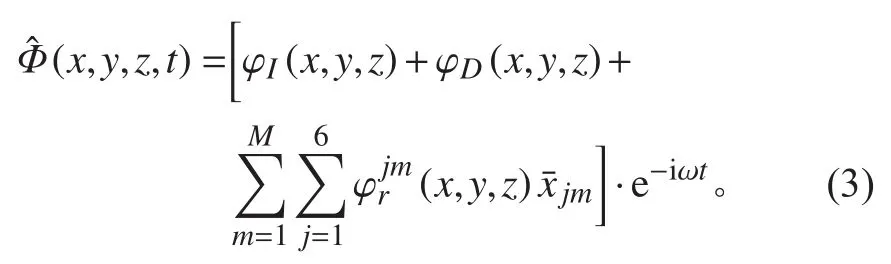
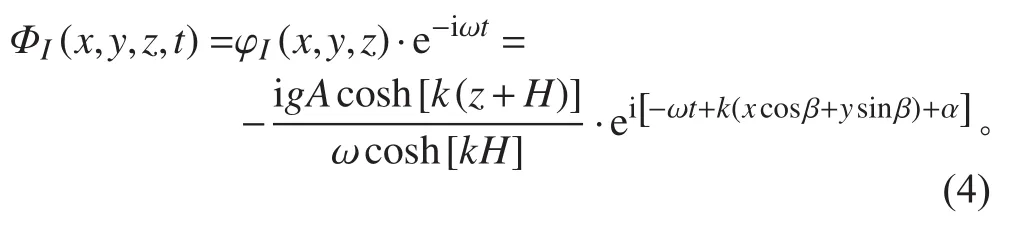
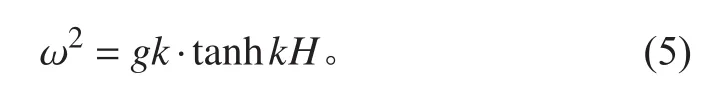
繞射勢與輻射勢均滿足拉普拉斯方程可在相應的邊界條件下采用格林函數法[12]求解。

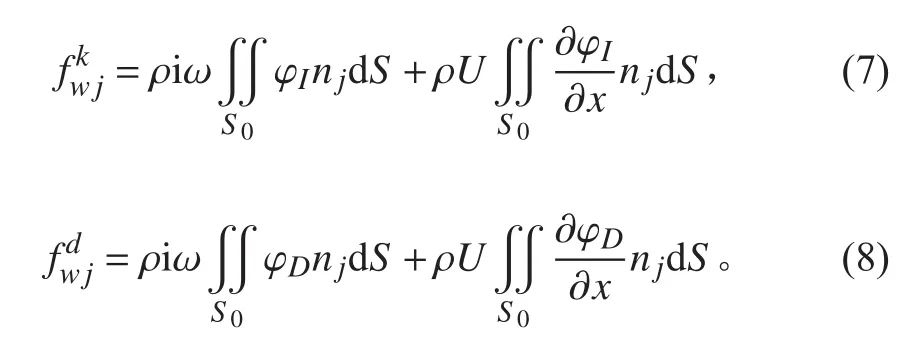
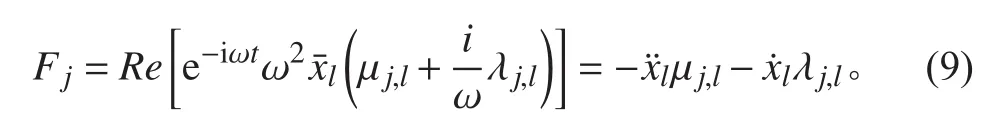
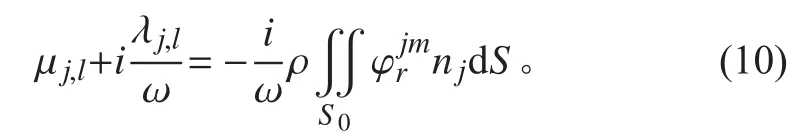
浮體的頻域運動方程為[11]：

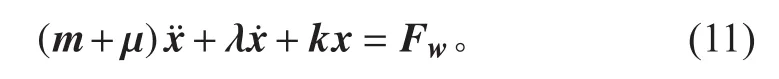
利用式（10）求得縱向連接多聯浮體結構的附加質量和附加阻尼，與波浪激勵力一起代入運動方程（11），即可求出縱向連接多聯浮體結構的運動響應。

2 數值模型

本文研究的縱向連接多聯浮體結構是由2個浮運高架結構單元通過鉸接接頭連接而成的，分別將2個浮體命名為S1與S2，其計算模型及坐標系定義如圖1所示。通過改變不同的水深、浪向角與航速分別對浮體結構進行水動力計算。設水深分別為10 m，8 m，5 m，3 m 和 2 m，浪向角分別為 0°，30°，45°，60°，90°和 180°，航速分別為 0 m/s，1.0 m/s，2.0 m/s，2.5 m/s和3.0 m/s時，對多聯浮體結構進行頻域特性分析。

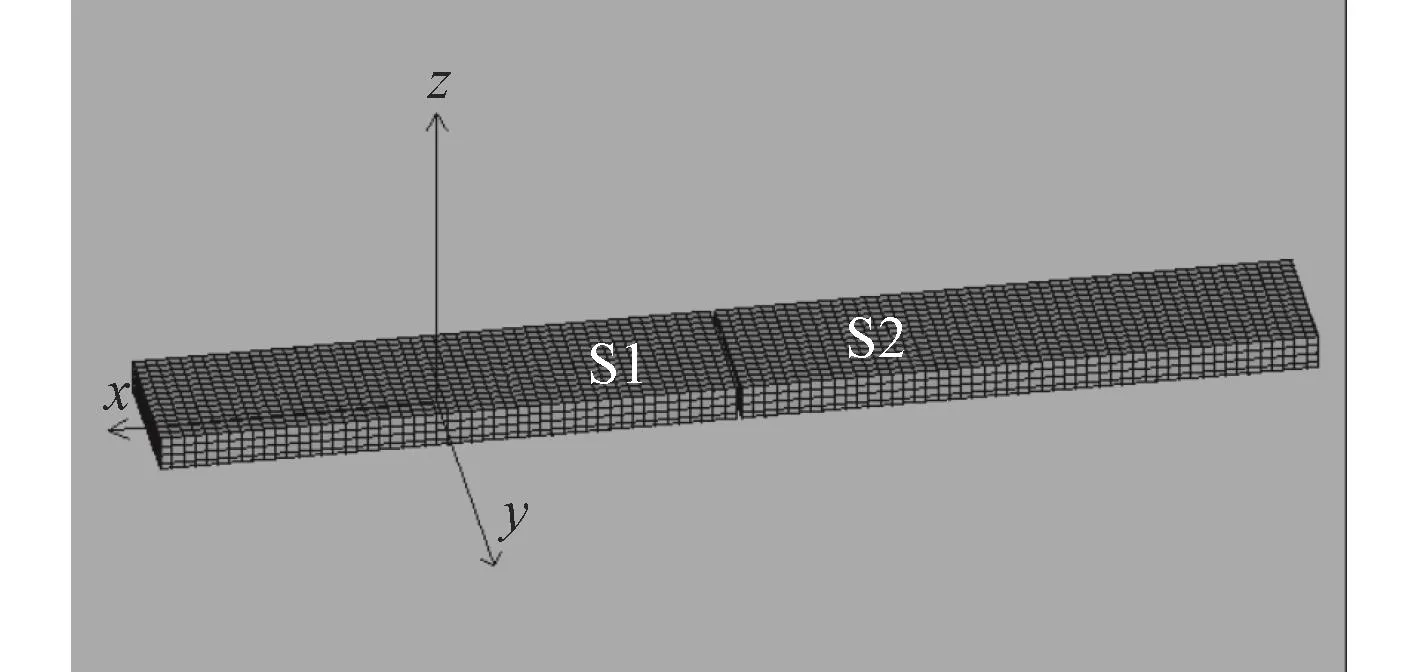
圖1 浮式結構網格劃分Fig.1 Floating structure meshing

表1 浮式結構幾何參數與力學參數Tab.1 Geometric and mechanical parameters of floating structures

3 計算結果與討論

垂蕩、縱蕩與首搖對縱向連接多聯浮體航行的影響較大，因此本文僅對此3個自由度進行討論。

3.1 水深對RAOs的影響

在研究水深對RAOs的影響中，本節設定2.5 m/s航速，0°和30°浪向，分別對2 m，3 m，5 m，8 m，10 m和無限水深的情況下進行數值模擬計算。由于0°浪向時對首搖RAOs不會產生影響，因此在本節0°浪向只對垂蕩與縱搖進行討論。

圖2和圖3分別為0°與30°浪向下浮體S1在不同水深時RAOs隨波浪圓頻率變化曲線。各浪向的垂蕩RAOs在頻率趨于0 rad/s時均趨于1，總體上垂蕩RAOs隨著水深的增加而增大，峰值周期也隨之增大。縱搖RAOs在低頻段隨著水深的增加而減小，在中頻段隨著水深的增加而增大。30°浪向的首搖RAOs在中低頻段隨著水深的減小而增大，在高頻段趨于穩定。在頻率小于0.3 rad/s時會引起較大的首搖RAOs，特別是水深小于5 m時會引起30°～40°的首搖RAOs，應引起重視。

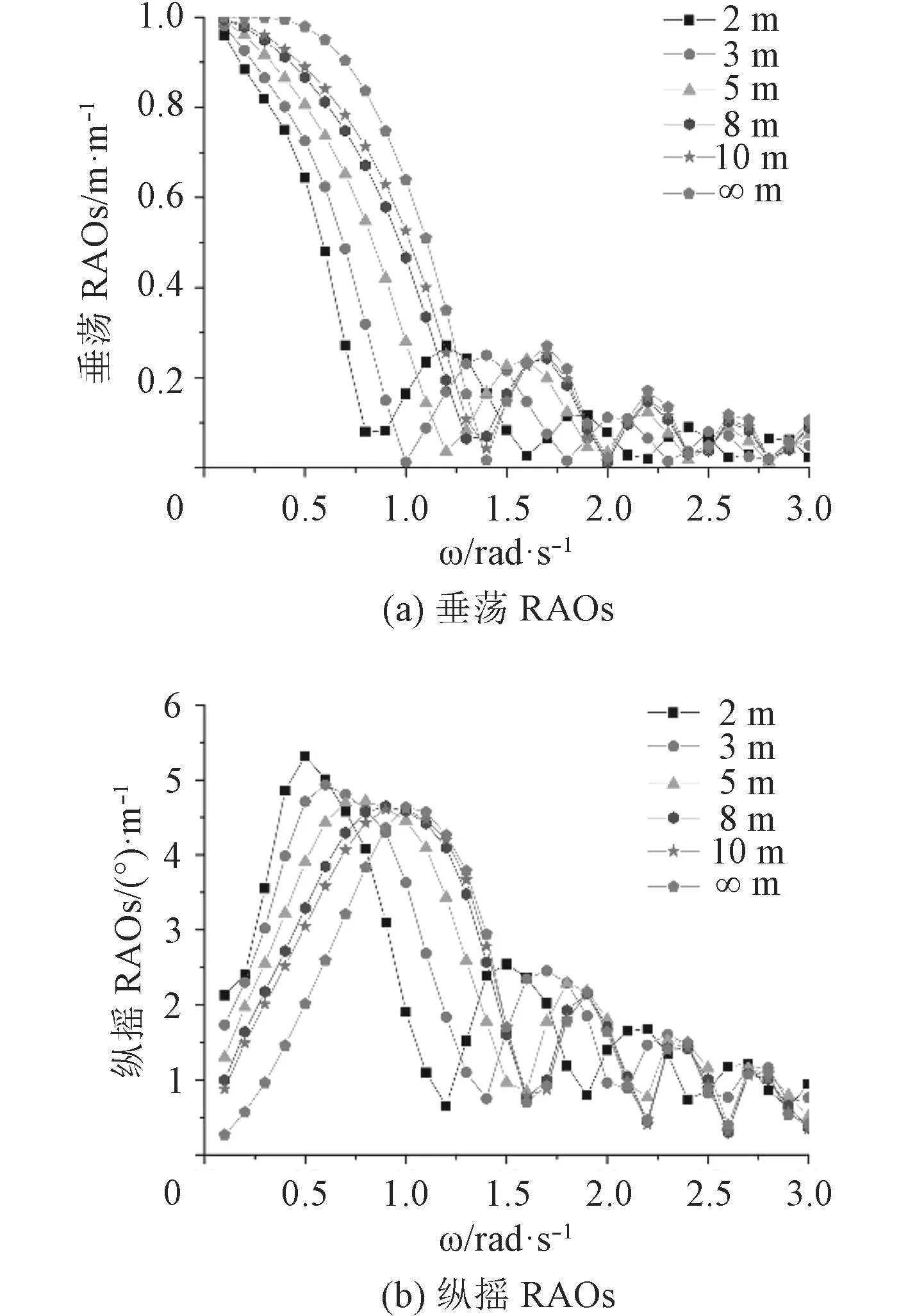
圖2 不同水深下垂蕩和縱搖RAOs隨頻率變化曲線（0°浪向，航速u=2.5 m/s）Fig.2 RAOs curves of Heave and Pitch with frequency at different water depths(0 degree wave direction,speed u = 2.5 m/s)

由圖2和圖3可以發現在8 m水深處各自由度RAOs值與無限水深時相比差別不大，因此對于本文研究的縱向連接多聯浮體，8 m以上水深可以看作無限水深進行分析和計算。由于淺水效應的存在，在5 m水深內會導致浮體縱搖RAOs與首搖RAOs偏高，因此在5 m水深內航行時應注意多聯浮體的運動響應。

3.2 浪向對RAOs的影響

在研究浪向對RAOs的影響中，本文設定2.5 m/s航速，5 m 水深，對 0°，30°，45°，60°，90°和 180°浪向進行數值模擬計算。圖4為浮體S1在不同浪向時RAOs隨波浪圓頻率變化曲線。

由圖4（a）可見，垂蕩RAOs各浪向在頻率趨于0 rad/s時均趨于1，并在90°浪向范圍內隨著浪向角的增加而增加。

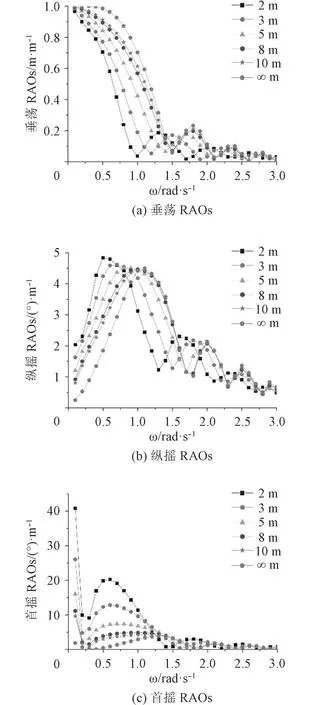
圖3 不同水深下垂蕩、縱搖和首搖RAOs隨頻率變化曲線（30°浪向，航速 u=2.5 m/s）Fig.3 RAOs curves of Heave, Pitch and Yaw with frequency at different water depths (30 degree wave direction,speed u = 2.5m/s)

由圖4（b）可見，縱搖RAOs在低頻段存在一個最大值，此最大值在90°浪向范圍內隨浪向角的減小而增大。

由圖4（c）可見，首搖RAOs主要在斜浪向條件下會產生較大的響應，尤其是在頻率小于0.3 rad/s時會產生20°左右的首搖應引起重視，在0.3～2.0 rad/s頻率段，斜浪向的最大首搖角也可達6°～8°，首搖響應在頻率變大時趨于穩定。

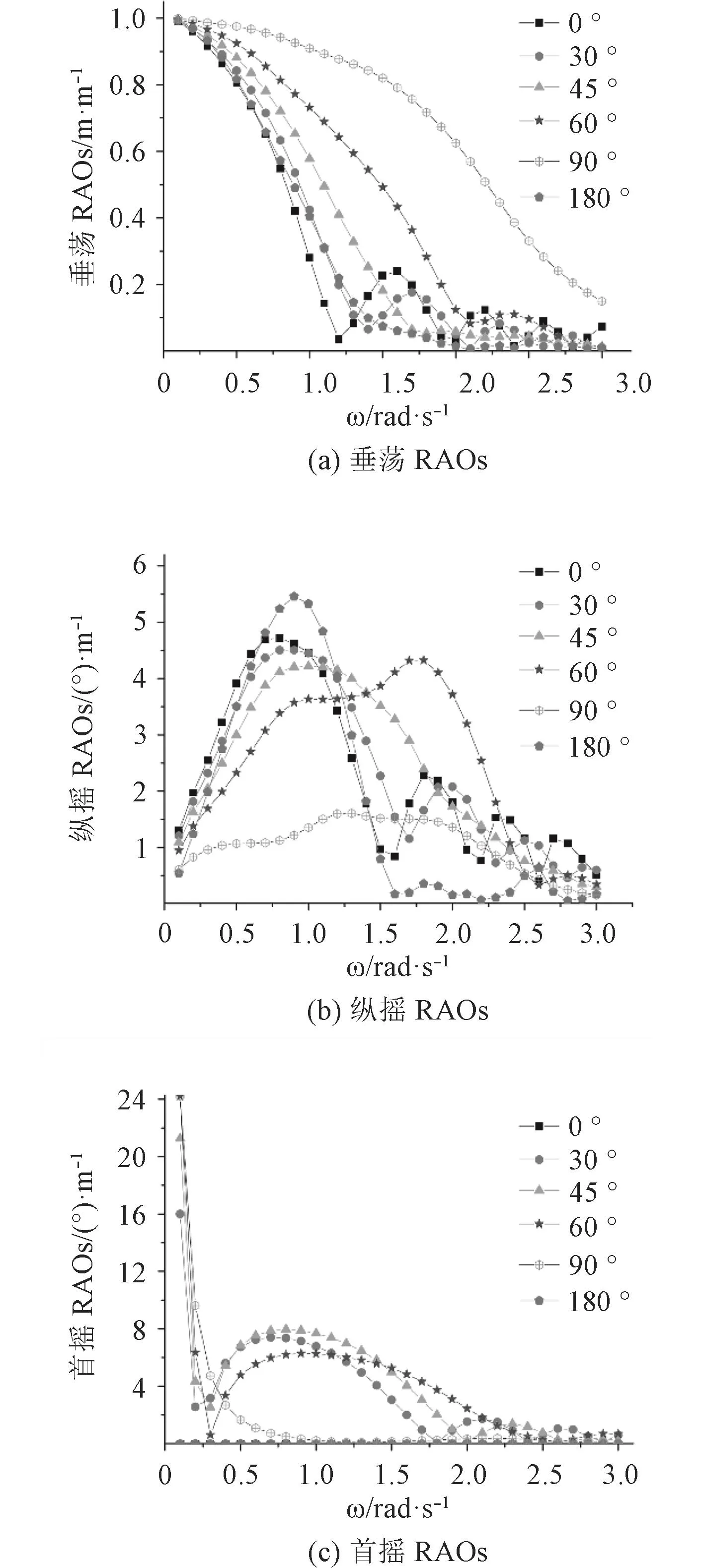
圖4 不同浪向下垂蕩、縱搖和首搖RAOs隨頻率變化曲線（水深5 m，航速u=2.5 m/s）Fig.4 RAOs curves of Heave , Pitch and Yaw with frequency in different wave direction (depth 5 m, speed u = 2.5 m/s)

綜合圖4及相關分析得出如下結論：垂直浪向（即90°浪向）航行時應多注意多聯浮體的垂蕩；在迎浪（0°浪向）與頂浪（180°浪向）航行時應多注意多聯浮體的縱搖，在以其他浪向航行時，應多注意多聯浮體的首搖。不同航向對應不同的波向角，因此，在縱向連接多聯浮體拖航過程中，可通過適當改變航向來減小某個自由度過大的響應。

3.3 航速對RAOs的影響

在研究航速對RAOs的影響中，本文設定30°浪向，5 m水深，分別對0 m/s，1.0 m/s，2.0 m/s，2.5 m/s和3.0 m/s航速進行數值模擬計算。圖5為浮體S1在不同航速時RAOs隨波浪圓頻率變化曲線。可見，垂蕩和縱搖RAOs受航速的影響較小，首搖RAOs隨航速的增加而增加，因此應盡量避免高航速拖航。

4 結 語

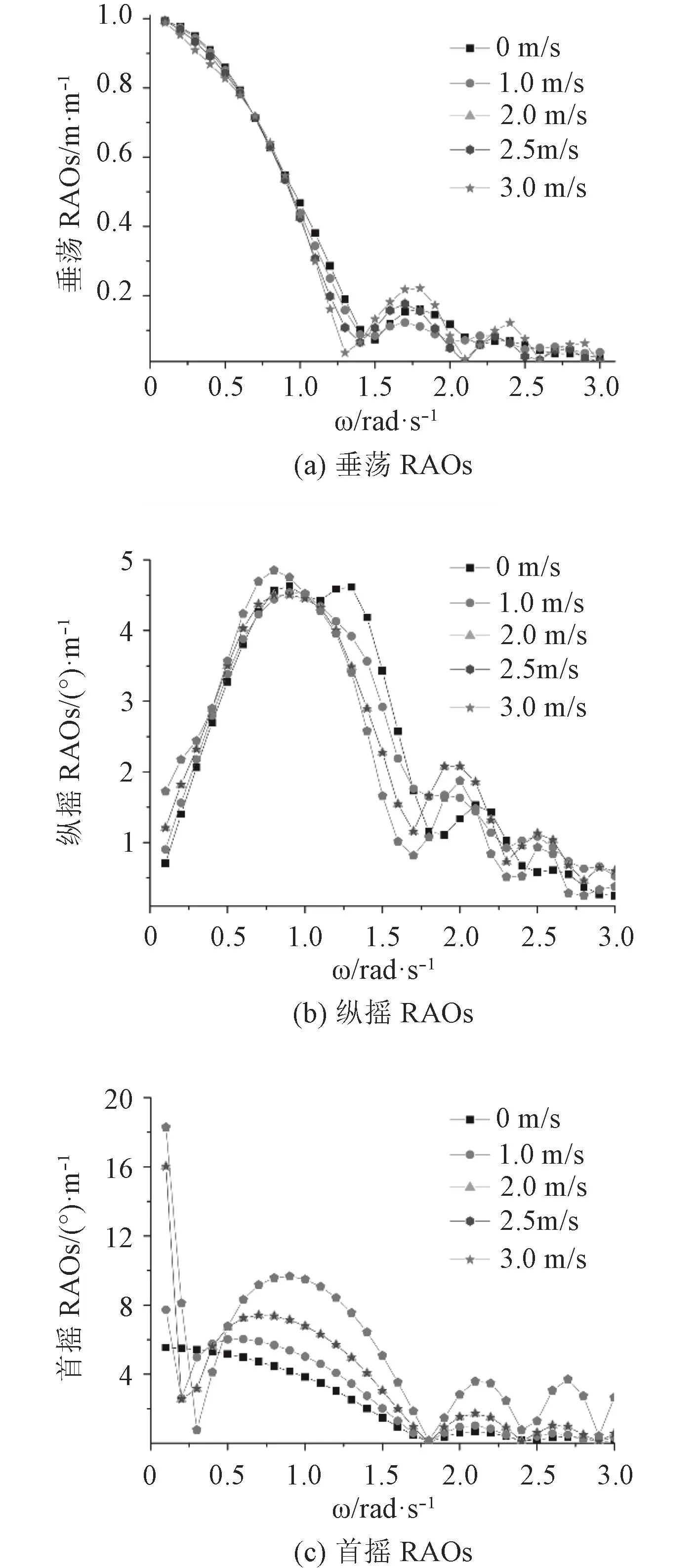
圖5 30°浪向、5 m水深不同航速下各自由度RAOs變化曲線Fig.5 RAOs curves of degree of freedom under different velocities of 30 degree wave direction and 5 m water depth

本文研究了有航速縱向連接多聯浮體的水動力特性，對比分析了水深、浪向及不同航速對浮體運動幅值響應算子的影響。通過對計算結果的分析得到以下結論：

1）水深對有航速縱向連接多聯浮體的運動響應影響較大，水深越淺，浮體的垂蕩RAOs越小，但在一定的頻率下會導致浮體縱搖與首搖產生較大的RAOs值。總體上，若在淺水中頻浪中航行，縱搖會隨著水深的減小而減小，而首搖不會產生過的RAOs值，是比較有利的。

2）垂直浪向（即90°浪向）航行時應多注意多聯浮體的垂蕩；在迎浪（0°浪向）與頂浪（180°浪向）航行時應多注意多聯浮體的縱搖，在以其他浪向航行時，應多注意多聯浮體的首搖。在縱向連接多聯浮體拖航過程中，可通過適當改變航向來減小某個自由度過大的響應。

3）航速對縱向連接多聯浮體垂蕩和縱搖RAOs影響較小，但對首搖RAOs的影響較為明顯。總體上航速越低，運動響應越小，所以拖航時的航速不宜過高。考慮到高頻段運動響應明顯小于中頻段，在波頻較高，即波長不大時可適當提高航速。