空間幾何測(cè)試題A

田煌英

一、選擇題

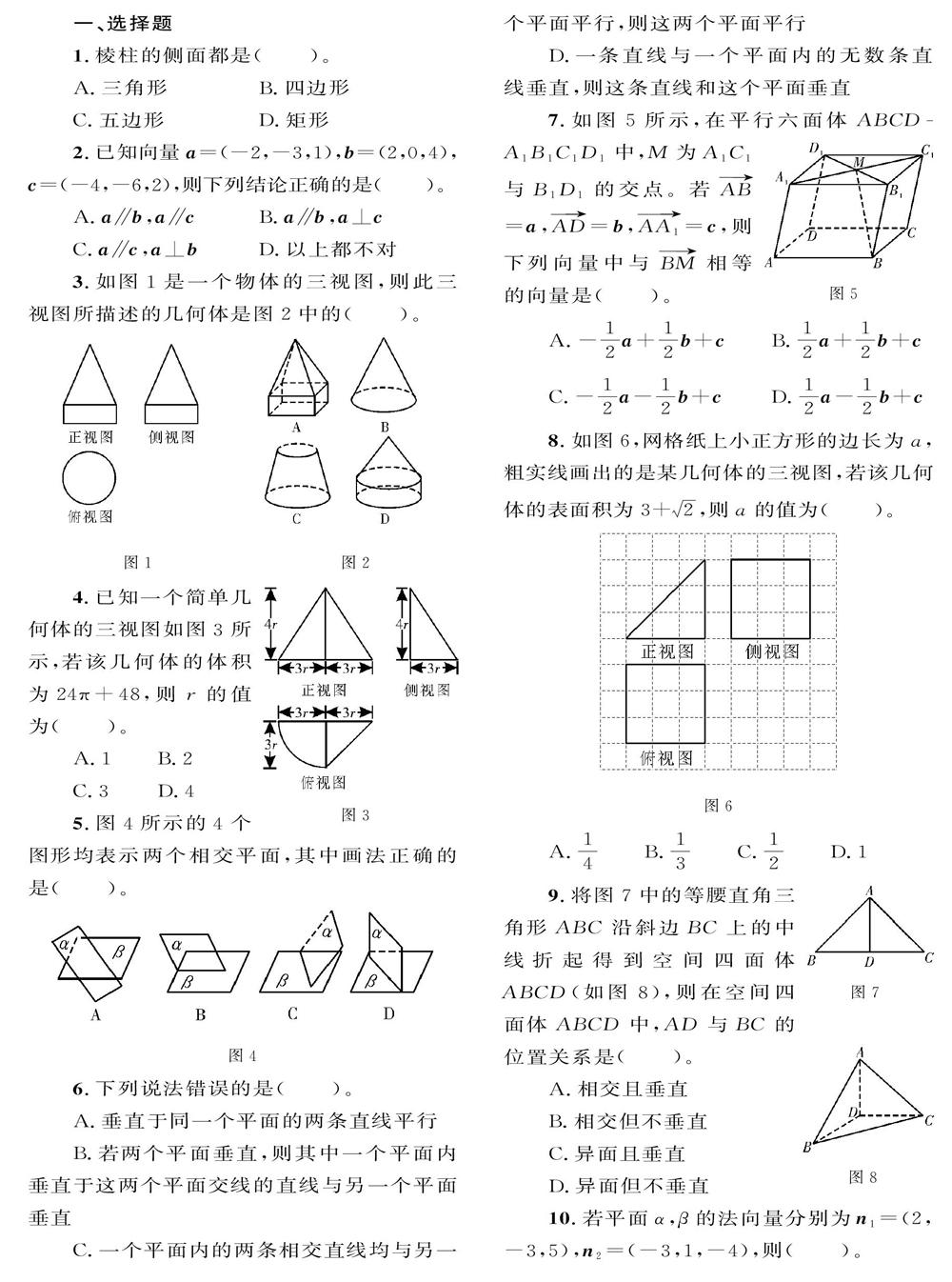
1.棱柱的側(cè)面都是（ ）。

A.三角形

B.四邊形

C.五邊形

D.矩形

2.已知向量a=（-2，-3，1），b=（2，0，4），c=（-4，-6，2），則下列結(jié)論正確的是（ ）。

A.a //b，a//c

B.a//b ，a⊥c

C.a∥c，n⊥b

D.以上都不對(duì)

3.如圖l是一個(gè)物體的三視圖，則此三視圖所描述的幾何體是圖2中的（ ）。

4.已知一個(gè)簡(jiǎn)單幾何體的三視圖如圖3所示，若該幾何體的體積為24π+48，則r的值為（ ）。

A.1

B.2

C.3

D.4

5.圖4所示的4個(gè)圖形均表示兩個(gè)相交平面，其中畫(huà)法正確的是（ ）。

6.下列說(shuō)法錯(cuò)誤的是（ ）。

A.垂直于同一個(gè)平面的兩條直線平行

B.若兩個(gè)平面垂直，則其中一個(gè)平面內(nèi)垂直于這兩個(gè)平面交線的直線與另一個(gè)平面垂直

C.-個(gè)平面內(nèi)的兩條相交直線均與另一個(gè)平面平行，則這兩個(gè)平面平行

D.-條直線與一個(gè)平面內(nèi)的無(wú)數(shù)條直線垂直，則這條直線和這個(gè)平面垂直

7.如圖5所示，在平行六面體ABCDAlBIC1D1中，M為A1C1與B1Dl的交點(diǎn)。若AB

=a，AD=b，AA1=c，則下列向量中與BM相等的向量是（ ）。

A. -1/2a+1/2b+c B.1/2a+1/2b+c

C. -1/2a- 1/2b+c

D.1/2a-1/2b+c

8.如圖6，網(wǎng)格紙上小正方形的邊長(zhǎng)為“，粗實(shí)線畫(huà)出的是某幾何體的三視圖，若該幾何體的表面積為3+√2，則a的值為（ ）。

A.1/4

B.1/3

C.1/2

D.1

9.將圖7中的等腰直角三角形ABC沿斜邊BC上的中線折起得到空間四面體ABCD（如圖8），則在空間四面體ABCD中，AD與BC的位置關(guān)系是（ ）。

A.相交且垂直

B.相交但不垂直

C.異面且垂直

D.異面但不垂直

10.若平面α，β的法向量分別為n1=（2，-3，5），n2=（-3，l，-4），則（ ）。

A.a//p

B.a⊥β

C.a，β相交但不垂直

D.以上均不正確

11.如圖9所示，體積為8的正方體ABCD -AlB1Cl Dl中，分別過(guò)點(diǎn)Al，C1，B作A1M，C1N，BP垂直于平面ACD1，垂足分別為M，N，P，則六邊形D.MAPCN的面積為（ ）。

A.4√3 B.4√6 C.12 D.12√2

12.如圖10，在三棱錐D-ABC中，AC-BD，且AC⊥BD，F(xiàn)，F(xiàn)分別是棱DC，AB的中點(diǎn)，則 FF和AC所成的角等于（ ）。

A. 30°

B. 45°

C. 60°

D. 90°

二、填空題

13.某網(wǎng)錐體的側(cè)面展開(kāi)圖是網(wǎng)心角為2π/3的扇形，當(dāng)側(cè)面積是27π時(shí)，則該圓錐體的體積是____ 。

14.已知正四棱錐PABCD的底面邊長(zhǎng)為2，表面積為12，則它的體積為_(kāi)__ 。

15.如圖ll所示，在正方體ABCD-A1BlClD1中，截面C1D1AB與底面ABC.D所成二面角C1 -AB-C的大小為_(kāi)__ 。

16.“網(wǎng)材埋壁”是我國(guó)古代數(shù)學(xué)著作《九章算術(shù)》中的一個(gè)問(wèn)題：“今有網(wǎng)材，埋在壁中，不知大小。以鋸鋸之，深一寸，鋸道長(zhǎng)一尺。問(wèn)徑幾何。”用現(xiàn)在的數(shù)學(xué)語(yǔ)言表述是：“如圖12所示，一網(wǎng)柱形埋在墻壁中，AB=1尺，D為AB的中點(diǎn)，AB⊥CD，CD=1寸，則網(wǎng)柱底面的直徑長(zhǎng)是__寸。”（注：1尺=lO寸）

三、解答題

17.已知某幾何體的俯視圖是如圖13所示的矩形，正視圖是一個(gè)底邊長(zhǎng)為8，高為4的等腰三角形，側(cè)視圖（或稱左視圖）是一個(gè)底邊長(zhǎng)為6，高為4的等腰三角形。

（l）求該幾何體的體積V;

（2）求該幾何體的側(cè)面積S。

18.如圖14所示，在直三棱柱ABC-A1BlC1，中，AB⊥AC，AC=AA1，D是棱AB的中點(diǎn)。求證：

（1）BC1∥平面A1CD;

（2）BC1⊥A1C1。

19.如圖15所示，在三棱錐P-ABC中，PA⊥平面ABC，∠BAC=60°，PA=AB=AC=2，E是PC的中點(diǎn)。

（1）求證：AE與PB是異面直線;

（2）求異面直線AE和PB所成角的余弦值;

（3）求三棱錐A-EBC的體積。

20.如圖16所示，在四棱錐P-ABCD中，已知PA上平面ABCD，△ABC為等邊三角形，PA=2AB=2，AC⊥CD，PD與平面PAC所成角的正切值為√15/3。

（1）證明：BC∥平面PAD;

（2）若M為PB上一點(diǎn)，且V=三棱M-PCD=√13/8，試判斷點(diǎn)M的位置。

21.如圖1 7，在△ABC中，AB=BC=2，∠ABC=90°，E，F(xiàn)分別為AB，AC邊的中點(diǎn)，以EF為折痕把△AEF折起，使點(diǎn)A到達(dá)點(diǎn)P的位置，且PB—BE，如圖18所示。

（1）證明：EF⊥平面PBF;

（2）設(shè)N為線段PF上的動(dòng)點(diǎn)，求直線BN與平面PCF

所成角的正弦值的最大值。

（責(zé)任編輯 王福華）