2019年高考數學模擬試卷（四)

本刊編輯部試題研究中心

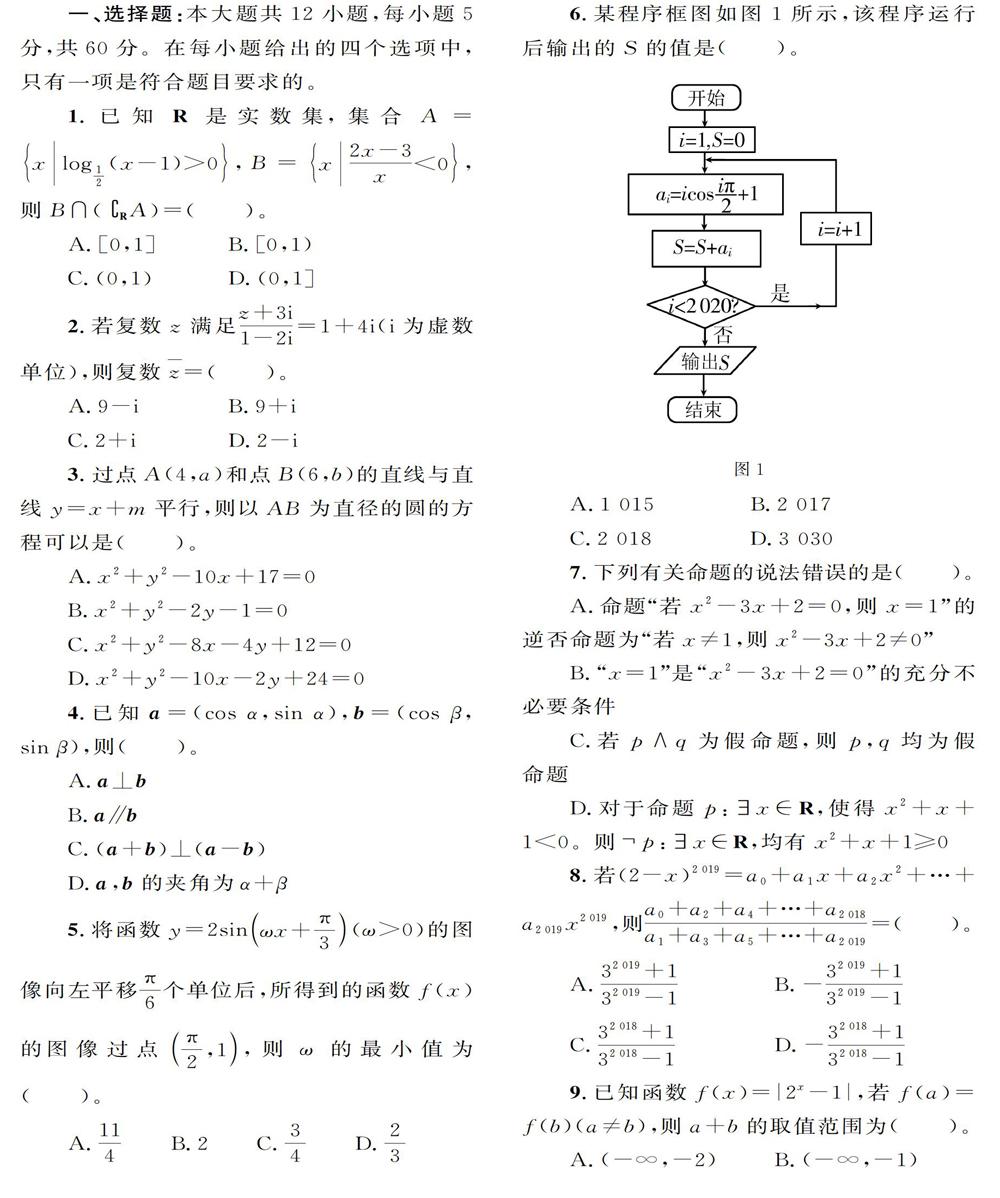
一、選擇題：本大題共12小題，每小題5分，共60分。在每小題給出的四個選項中，只有一項是符合題目要求的。

18.（本小題滿分12分）

某社區為了豐富居民節日活動，組織了“迎新春”象棋大賽，已知由1，2，3號三位男性選手和4，5號兩位女性選手組成混合組參賽。已知象棋大賽共有三輪，設三位男性選手在一至三輪勝出的概率依次是5/6，3/5，2/3;兩位女性選手在一至三輪勝出的概率依次是3/4、2/3、1/2。

（1）若該組五名選手與另一組選手進行小組淘汰賽，每名選手只比賽一局，共五局比賽，求該組兩名女性選手的比賽次序恰好不相鄰的概率;

（2）若一位男性選手因身體不適退出比賽，剩余四人參加個人比賽，比賽結果相互不影響，設X表示該組選手在四輪中勝出的人數，求隨機變量X的分布列和數學期望。

19.（本小題滿分12分）

如圖3，半圓o的直徑AB長為4，C是半圓O上除A，B外的一個動點，DC垂直于半圓O所在的平面，DC∥EB，DC=EB，

分析：（1）先化簡再利用正弦函數的單淵性得出減區間。

（2）先直接根據平移和伸縮變換得到g（x）的提示式，再根據正弦函數的值域求得結論。

（責任編輯 王福華）