汽輪機熱力性能指標公式推導及驗證

呂海禎, 丁立新

(國網山東省電力公司電力科學研究院， 濟南 250003)

為了從熱力學的角度，對再熱回熱汽輪機性能進行具體的理論分析，比照簡單朗肯循環的熱力學分析，需要知道理想比內功率、相對內效率、理想循環效率、理想循環的平均吸熱溫度和平均放熱溫度等熱力性能指標。通過這些指標，把熱力學和熱力工程兩個領域聯系起來，更有利于從理論與實踐相結合上實現兩個專業的全面協作；因此，有必要確定再熱回熱汽輪機的這些熱力性能指標。筆者以典型的一次再熱八級回熱凝汽式汽輪機為例，對這些熱力性能指標進行公式推導、驗證和分析討論。

1 熱力性能指標公式推導

1.1 理想比內功率

一次再熱八級回熱凝汽式汽輪機的絕對內效率可表示為：

(1)

式中：ηi為汽輪機絕對內效率；αj、αrh、αc分別為汽輪機進汽1 kg時1～8級抽汽、中壓缸進汽、低壓缸排汽份額；h0、hfw分別為汽輪機自動主汽門前實測的進汽焓、鍋爐省煤器入口實測的給水焓，kJ/kg；qrh為再熱蒸汽吸熱量，kJ/kg；Δhj為抽汽在汽輪機中的實際焓降，kJ/kg，再熱前Δhj=h0-hj，再熱后Δhj=h0+qrh-hj，hj為汽輪機1～8級抽汽焓，kJ/kg；Δhc為凝汽在汽輪機中的實際焓降，kJ/kg，Δhc=h0+qrh-hc，hc為低壓缸排汽與凝汽器喉部結合面排汽焓，kJ/kg。

該汽輪機高壓缸有2級抽汽，第2級抽汽為高壓缸排汽；中、低壓缸各3級，第5級抽汽為中壓缸排汽；機組共有8級抽汽。

式(1)分子第一項可寫為：

(2)

式中：Δhsj為抽汽對應的等熵焓降，kJ/kg；ηj為抽汽點的級段效率；ΔhsH為自動主汽門前至高壓缸排汽對應的等熵焓降，kJ/kg，ΔhsH=h0-hsH，hsH為高壓缸排汽的等熵焓，kJ/kg；ηH為高壓缸效率；ΔhsI為中聯門至中低壓連通管中點對應的等熵焓降，kJ/kg，ΔhsI=hrh,out-hsI，hrh,out為中壓缸中聯門前實測蒸汽焓，kJ/kg，hsI為中低壓連通管中點的等熵焓，kJ/kg；ηI為中壓缸效率。

在高壓缸中， 自動主汽門前至第1級抽汽點對應等熵焓降及級段效率為Δhs1=h0-hs1及η1，hs1為第1級抽汽點等熵焓，kJ/kg；自動主汽門前至第2級抽汽點對應等熵焓降及級段效率為Δhs2=h0-hs2及η2，hs2為第2級抽汽點等熵焓，kJ/kg。

顯然，Δhs2=ΔhsH，hs2=hsH，η2=ηH。

在中壓缸中，中聯門至第3級抽汽點對應等熵焓降及級段效率為Δhs3=hrh,out-hs3及η3，hs3為第3級抽汽點等熵焓，kJ/kg；中聯門至第4級抽汽點對應等熵焓降及級段效率為Δhs4=hrh,out-hs4及η4，hs4為第4級抽汽點等熵焓，kJ/kg；中聯門至第5級抽汽點對應等熵焓降及級段效率為Δhs5=hrh,out-hs5及η5，hs5為第5級抽汽點等熵焓，kJ/kg。

顯然，Δhs5=ΔhsI,hs5=hsI，η5=ηI。

在低壓缸中，中低壓連通管中點至第6級抽汽點對應等熵焓降及級段效率為Δhs6=hL,in-hs6及η6，hL,in為中低壓連通管中點實測蒸汽焓，kJ/kg，其值等于第5級抽汽點蒸汽焓h5，hs6為第6級抽汽點等熵焓，kJ/kg；中低壓連通管中點至第7級抽汽點對應等熵焓降及級段效率為Δhs7=hL,in-hs7及η7，hs7為第7級抽汽點等熵焓，kJ/kg；中低壓連通管中點至第8級抽汽點對應等熵焓降及級段效率為Δhs8=hL,in-hs8及η8，hs8為第8級抽汽點等熵焓，kJ/kg；中低壓連通管中點至低壓缸排汽點對應等熵焓降及低壓缸效率為ΔhsL=hL,in-hsL及ηL，hsL為低壓缸排汽與凝汽器喉部結合面對應的等熵焓，kJ/kg。

式(1)分子第二項可寫為：

αcΔhc=αc(ΔhsHηH+ΔhsIηI+ΔhsLηL)

(3)

實際比內功等于式(2)+式(3)，即

αLΔhsLηI+αcΔhsLηL

(4)

式中：wi為汽輪機實際比內功，kJ/kg；αL為低壓缸進汽份額。

當損失為零時，實際比內功wa等于理想比內功：

(5)

1.2 理想循環效率

把規定的抽汽等熵焓降、高中低壓缸等熵焓降代入式(5)并整理得：

wa=(h0+αrhhrh,out+αLhL,in)-

(6)

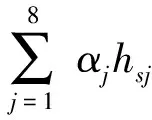
(7)

式中：ηt為理想循環效率；q0為比循環凈吸熱量，kJ/kg。

1.3 理想循環平均吸熱溫度、放熱溫度

理想比內功等于實際比內功時，蒸汽在汽輪機中絕熱等熵膨脹，損失為零，過程熵增為零：

Δswa=0

(8)

比循環凈吸熱量熵增：

Δsq0=s0-sfw+αrh(srh-sH)

(9)

式中：Δsq0為工質在循環吸熱過程中的熵增，kJ/(kg·K)；s0為自動主汽門前蒸汽熵，kJ/(kg·K)；sfw為省煤器入口給水熵，kJ/(kg·K)；srh為中聯門前蒸汽熵，kJ/(kg·K)；sH為高壓缸排汽熵，kJ/(kg·K)。

(10)

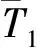
1.4 汽輪機相對內效率

把規定的抽汽實際焓降、高中低壓缸實際焓降代入式(4)并整理得：

(11)

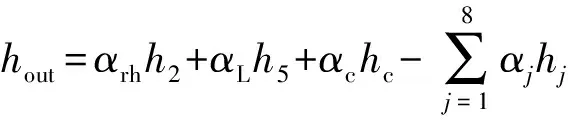
(12)

1.5 汽輪機熱耗率

對于再熱回熱循環的凝汽式汽輪機，應采用熱耗率HR作為性能評價指標。

ηriηtηmηgHR=3 600

(13)

式中：ηm為機械效率；ηg為發電機效率；HR為熱耗率，kJ/(kW·h)。

對式(13)取對數求微分整理得：

(14)

對式(14)求積分并整理得：

(15)

式中：HR,X為汽輪機結構改進后熱耗率，kJ/(kW·h)；ηri,X為汽輪機結構改進后的相對內效率；ηt,X為改進后理想循環效率；ηm,X為汽輪機結構改進后機械效率；ηg,X為汽輪機結構改進后發電機效率；C為常數。

2 熱力性能指標驗證及討論

2.1 機組熱力系統概況

為進一步驗證以上推導的性能指標，假定上述已知汽輪機容量為660 MW，高中壓合缸，三缸四排汽，三高加一除氧四低加，疏水逐級自流。熱力系統見圖1。

HP—高壓缸；YP—壓汽機；IP—中壓缸；2LP—雙低壓缸；G—發電機；HD—除氧器
圖1 超超臨界660 MW三缸四排汽凝汽式汽輪機的熱力系統圖

2.2 熱力性能指標驗證

設計3組原則性熱力系統，計算結果見表1。

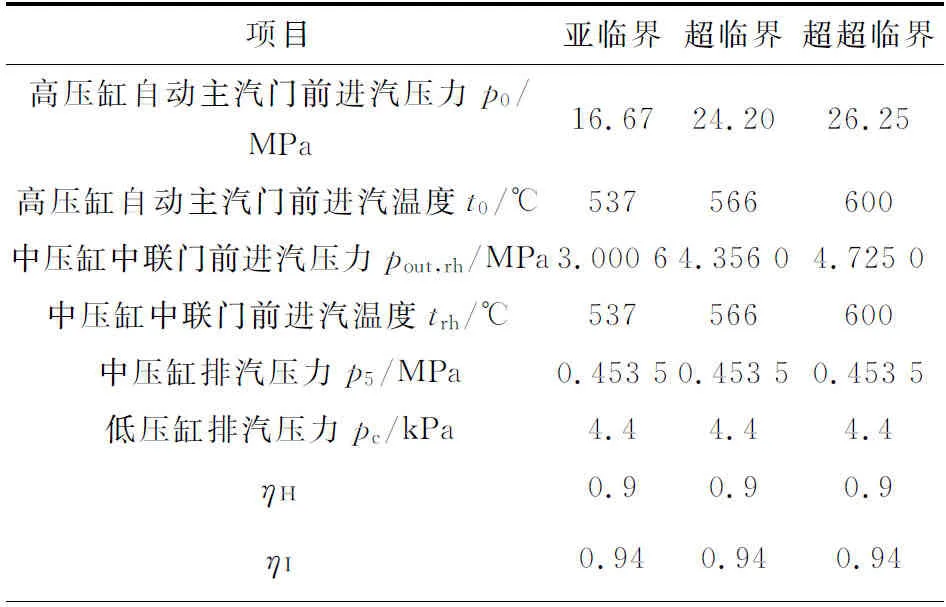
表1 660 MW原則性熱力系統主要設計結果

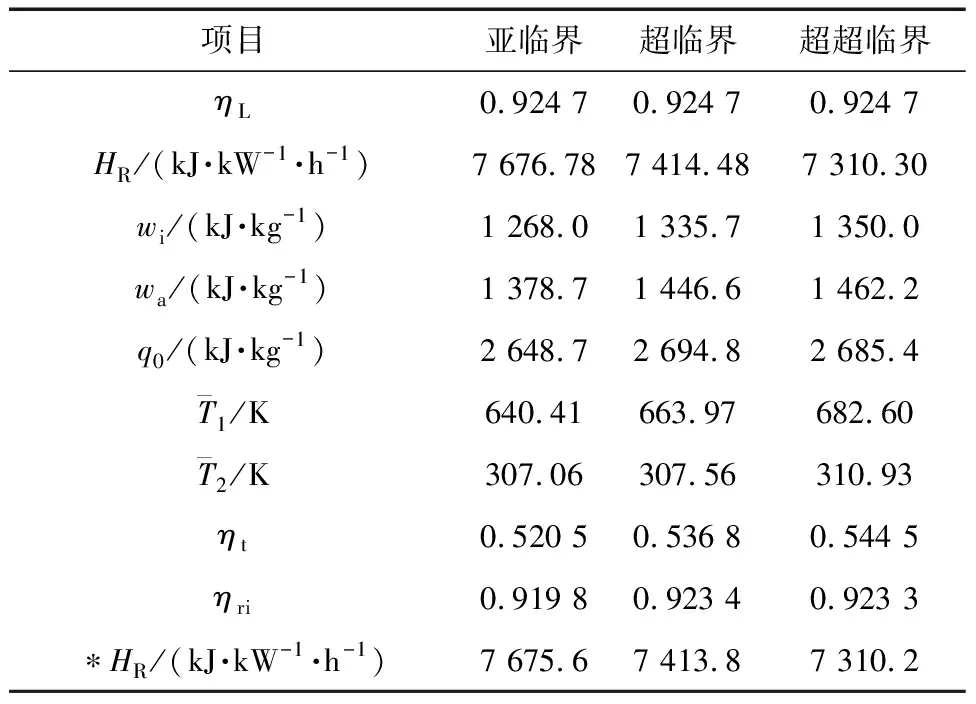
表1(續)

表1中HR是根據原則性熱力系統能量與流量平衡原則設計計算的[1]，*HR是根據公式(13)計算的，公式(13)中理想循環效率根據公式(7)、汽輪機內效率根據公式(12)計算，HR與*HR的一致性，進一步驗證了推導的公式正確。

對表1中亞臨界和超臨界的進汽參數進行比較。理想循環平均吸熱溫度提高23.56 K；理想循環平均放熱溫度分別為307.063 K、307.56 K，理想循環效率提高1.63百分點。汽輪機相對內效率分別為91.98%、92.34%。汽輪發電機組熱耗率降低261.8 kJ/(kW·h)。

表1中超超臨界壓力進一步提高，進汽溫度也提高到600 ℃。理想循環平均吸熱溫度提高18.63 K；理想循環平均放熱溫度提高3.37 K，理想循環效率提高0.77百分點。汽輪機相對內效率分別為92.34%、92.33%。汽輪發電機組熱耗率降低103.6 kJ/(kW·h)。

根據式(15)計算，超臨界時C=4.57 kJ/(kW·h)，超超臨界時C=0.73 kJ/(kW·h)。假定另一超超臨界機組的機械效率、發電機效率與表1相同，機械效率0.99，發電機效率0.989 5，汽輪機理想循環效率由54.45%提高到56.4%，相對內效率由92.33%提高到94.33%，根據式(15)計算效率提高后的熱耗率約為6 897.695 kJ/(kW·h)。

式(14)推導的假定前提是汽輪機內效率與理想循環效率是相互獨立的，但從表1來看：在高、中、低壓缸內效率不變的情況下，隨著理想循環效率的增大，汽輪機內效率也略有變化，這說明兩個效率是相關的。這樣在根據式(15)計算時，假定一個效率不變，提高另一個效率計算熱耗率的變化量，就會產生不確定度。

2.3 高壓缸改進措施

高壓缸效率0.9，結構方面的主要改進措施是：汽輪機配汽機構由傳統型的噴嘴調節改為旁通調節，去除了調節級。調節級的焓降由重新設計的2～3級內效率比較高的速度級承擔。調節級承擔的焓降大，做功能力強，效率特別低。一般超高壓機組加裝一級調節級后變成了亞臨界機組，亞臨界機組加裝一級調節級后變成了超臨界機組，使用調節級的好處是減少了耐高溫優質合金鋼材的應用，減少了制造成本，在汽輪機價格一定的情況下，對制造廠有利。由于調節級余速不能被下一級利用、存在斥汽損失和鼓風損失并且漏汽損失特別大，因此相比其后的壓力級，整級效率特別低，又加上它承擔的焓降占整個高壓缸焓降份額特別大，導致高壓缸效率特別低，不利于電廠節能減排。

2.4 中壓缸改進措施

中壓缸效率0.94，采取的主要措施是：變反動度設計的全三維-彎扭的葉片成型技術，減少了靜葉和動葉損失；采用了窄葉片，增加了通流級數，減少了余速損失[2]。

2.5 低壓缸改進措施

低壓缸效率0.924 7，采取的主要措施是：(1)按增大的排汽體積流量選取合適的排汽喉部面積的長葉片，每個特定的葉片有一個最佳的排汽體積流量，使余速損失最小[2]；(2)低壓末級彎扭靜葉，高效的帶前傾的J形馬刀型靜葉片，使靜葉損失最小[3]；(3)去濕技術，即加大動靜軸向間距、表面有抽吸槽的空心靜葉、減薄靜葉出汽邊、動葉進汽邊激光硬化技術，使濕汽損失最小[4]。

2.6 壓汽機改進措施

高中壓內缸也為合缸，高中壓轉子的前汽封之間去掉平衡軸向推力的高壓平衡活塞，由壓汽機替代。壓汽機進口通過內缸上的圓孔與內外缸夾層連通，夾層與高壓缸排汽連通；壓汽機出口與高壓缸前汽封連通。工作時，壓汽機把高壓缸排汽升壓后作為高壓缸前汽封的密封汽，密封、冷卻高壓前汽封。中壓缸前汽封與壓汽機進口連通，高壓缸排汽作為密封汽，阻止中壓缸前汽封漏汽。通過中壓缸上的內外缸夾層密封止口，保證高壓排汽不會流到中壓缸排汽口。高壓前汽封漏汽量為零，機組經濟性提高[3]。結構示意圖見圖2。

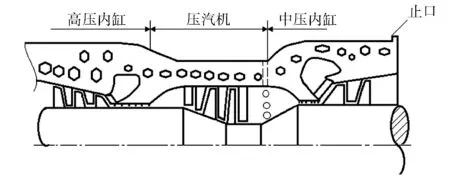
圖2 高中壓內缸合缸中間加裝壓汽機結構示意圖

3 結語

已有文獻中，簡單朗肯循環的理想循環效率、汽輪機內效率、循環平均吸熱溫度和循環平均放熱溫度熱力性能指標有計算公式[6]，但實際再熱回熱的復雜循環，無對應性能指標公式，只能是根據溫熵圖或焓熵圖進行定性分析。筆者確定了實際再熱回熱循環的性能指標計算公式，解決了實際再熱回熱循環性能指標無法計算的難題。