優化K 均值聚類在冗余特征剔除中的應用研究?

李麗敏 溫宗周 宋玉琴

（西安工程大學電子信息學院 西安 710048）

1 引言

隨著信號處理技術在機械故障診斷領域的應用越來越頻繁，許多隱藏在振動信號中的特征被挖掘出來，為精確地診斷某種機械故障提供了研究基礎［1～2］。近年來，由信號處理技術提取的特征包括時域特征、頻域特征和時-頻域特征。時域特征如偏度、峭度和根均值方差等，可以反映信號在整個周期內的變化情況［3］；頻域特征如傅里葉變換和快速傅里葉變換，能夠獲得振幅譜和功率譜的分析結果［4］；時頻域特征如小波包能量和希爾伯特邊緣譜能夠在時域和頻域共同交叉的方面分析信號［5］。上述特征可以通過組合為高維特征集合共同決策當前的故障類型，能夠提高診斷精度，但由此帶來的嚴重問題是隨著特征的增多，計算復雜度越來越大，訓練分類器的難度增加，而且訓練出來的分類器魯棒性變差。因此目前，怎么樣平衡計算復雜度和診斷精度之間的矛盾成為研究熱點。

為了減少計算復雜度，傳統的方法是直接減少特征的維數，相關的方法包括局部線性嵌入（LLE）［6］、局部保留投影（LPP）［7］和主成分分析（PCA）［8］。這些方法通過空間映射降低特征的維數，但在本源特征集合中，有些特征本身就對診斷起到相反的作用，對于得到診斷結果是不利的，這也會降低診斷精度，特別是當使用支持向量機方法（SVM）［9］用于機械故障診斷的分類器時，對特征的依賴性很強，因此特征集合的優劣影響SVM分類器的性能。

為了解決上述問題，本文從特征集合本身出發，采用基于K 均值聚類［10］的冗余特征剔除方法，將對診斷作用不大或者相反的特征剔除掉，保留最有利于診斷的那些特征，剔除冗余特征后的特征集合再用于訓練分類器時，即能保持原多個特征用于診斷時對精度的提高，同時能夠降低時間復雜度，有效地平衡時間和精度之間的矛盾。

2 基于特征權值優化的K均值聚類

K 均值聚類能夠將包含n 個數據的數據集合X={X1，X2，…，Xn}分 割為k 類，其中Xi=(xi，1，xi，2，…，xi，m)表示每個數據被提取了m維特征［11～14］。

K均值聚類的目標函數如下：

式（1）中，U（n*k 維）是由優化上述目標函數計算出的分割矩陣，U 中的元素ui，l=1 表明第i 個數據屬于l 類。 Z={Z1，Z2，…，Zk}是由K 均值聚類計算出的聚類中心，d(xi，j，zl，j)是第i 個數據和第j 個數據之間的距離，可由式（2）計算得出。

式（1）的約束條件為式（3）。

式（3）的約束條件指數據集X 中的每個數據只能歸屬于1 類。優化式（1）的目的是通過最小化目標函數P求解出U和Z。

為了計算出每個特征的權值，本文中，在K 均值聚類的目標函數P 中加入了這個權值W，因此獲得了一個新的K均值目標函數：

其中β 為ωj的系數。

通過式（4），可以計算出K 均值聚類出的每個特征的權重。

3 基于K 均值聚類的冗余特征剔除在SVM 多分類的機械故障診斷中的應用

通過K 均值聚類方法獲取到所有特征的權值后，剔除冗余特征的步驟如下：

1）設置權值閾值η；

2）將求出的每個權值wi(1 ≤i ≤m)與設置的閾值η 比較；

3）如果wi≤η，則剔除該特征；

4）如果wi＞η，保留該特征；

5）將數據集合按照保留下來的特征重新組合。

SVM 的基本思想是通過非線性變化將數據從原始空間映射到高維特征空間，從而找到最優的分割超平面，該超平面擁有最大的邊界從而將數據集合進行分類。一般的SVM 分類器主要用于1 對1或者1 對多的分類情況，但現實情況是，同一條件下可能有各種故障都需要分類出來，因此本文針對該種情況，選擇1 對多的分類器。具體操作步驟如下：

1）采集機械設備的振動信號，提取特征，按照序列排序；

2）從上述信號中取部分信號xi(xi∈RD，i=1，2，…，l)作為訓練樣本，同時為這些樣本設置訓練標簽；將xi和yi輸入給SVM 的目標函數，如式（5）所示。

通過解式（5），可以獲得權值ω ∈Rn，b ∈R，松弛變量ξi和懲罰因子C。

上述函數的約束函數如式（6）所示。

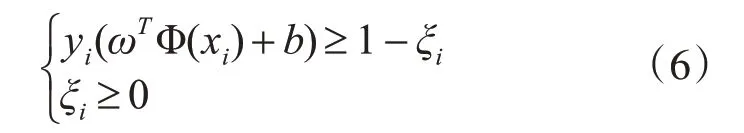
由此，xi被映射到高維的特征空間，在這個特征空間中，找到優化的分類超平面，決策函數如式（7）所示。

3）該函數設置的初衷是用于二分類的，因此當用于K 分類時，具體做法是將K 個二分分類器組合起來。

4 實驗驗證與分析

為驗證本文方法的有效性，利用凱斯西儲大學軸承實驗室的實驗數據作為測試數據［15］。選擇軸承的型號為6203-2RS JEM SKF，選取其中的正常狀態、內圈故障和外圈故障的振動加速度數據，這些數據采集于電機運行于1797r/s 的速度下，內圈故障和外圈故障的損失程度為0.1778mm，采樣頻率為12kHz，如圖1所示，為本文選取的三組測試數據原始采樣值的曲線，橫坐標（Sample point）表示采樣點，縱坐標（Amplitude）表示每個采樣點的振動幅值。

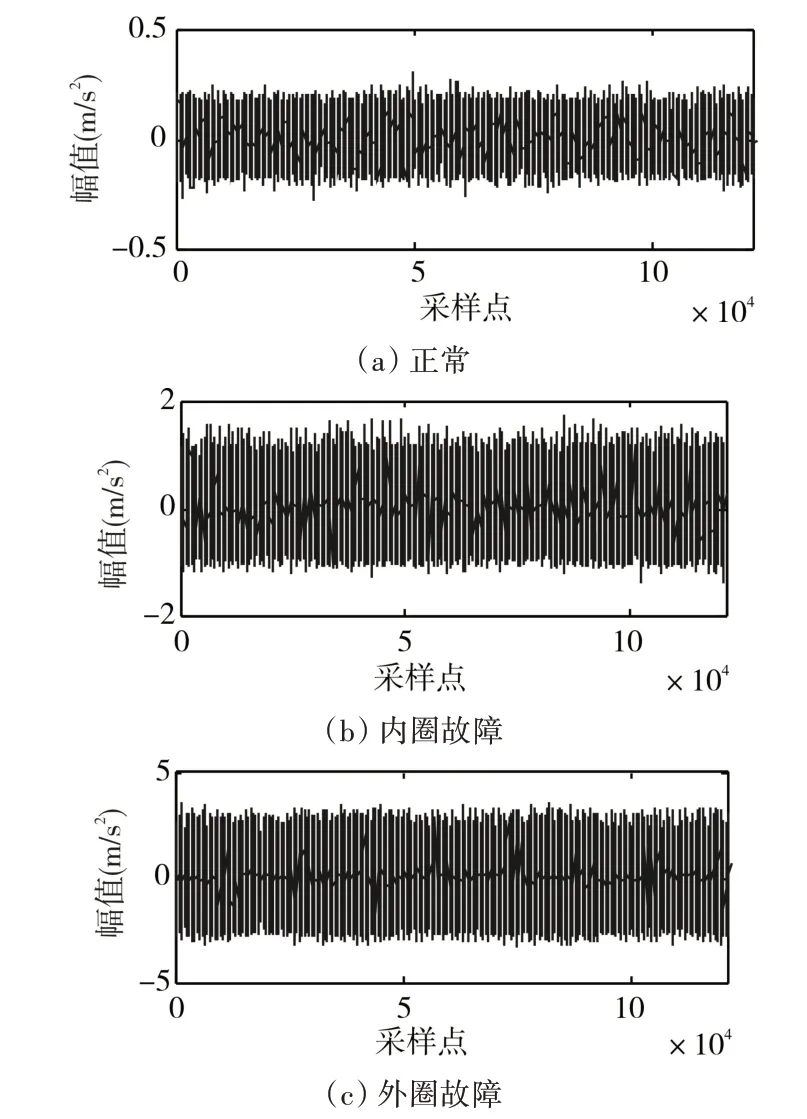
圖1 三組用于測試的振動加速度原始信號曲線

對三種原始振動信號分別提取了32 種特征，這些特征既包含時域特征、頻域特征，還包含時頻域混合特征，利用第2 節中所述方法，計算出每種特征用于3分類時的權值，即貢獻率，結果如下：

根據上述計算出的權值，當分別將閾值設置為 η(1)=4.9386e-06 ，η(2)=5.6806e-05 ，η(3)=0.0002，和η(4)=0.0034 時，會分別剔除掉2 個、7個、12個和22個冗余特征，則剩余有用特征分別為30 維、25 維、20 維和10 維。為比較本文方法與一般的LLE、LPP 和PCA 方法的性能，對相同的振動數據的32 維特征，利用上述三種方法也分別選擇出30維、25維、20維和10維特征。

利用SVM 多分類器對每種故障的100 個多維故障數據樣本進行訓練，得到多分類器；將三種類型數據的50 個樣本點混合后輸入給訓練好的SVM多分類器中，觀察診斷誤差和診斷所需時間。如圖2所示為本文方法剔除冗余特征后，剩余25維特征時，與利用LLE、LPP和PCA提取25維特征后，進行多分類的結果，從圖中可以直觀看出，本文方法在對正常、軸承內圈故障和軸承外圈故障進行分類時，分錯的數據點僅有1 個，說明本文方法優于其他三種方法。

圖2 本文方法與LLE、LPP和PCA方法在降維后利用同一多分類器進行故障診斷的性能比較

為全面驗證，其他相關實驗開展了對30 維、20維和10 維特征下故障診斷性能的比較，比較結果如表1所示。

表1 本文方法與LLE、LPP和PCA方法在分類準確率性能方面的比較

表1 所示，本文方法在4 種維度下，采用SVM多分類器診斷的結果表明，本文方法的診斷準確率均高于其他三種方法，甚至在利用本文方法將特征維數降低到10 維后，其診斷準確率仍高于其他三種方法，從而驗證了本文所提方法的有效性。為驗證本文方法在解決時間復雜度和診斷準確率之間的矛盾所做工作的有效性，冗余特征剔除后，進行SVM 多分類時，記錄了其運行時間。前提條件為，采用計算機主機頻率為2.5GHz。比較結果如表2所示，很明顯維度越低，時間耗費越小，32 維和10維之間時間消耗相差約4倍。

表2 時間復雜度性能比較

綜合分析表1和表2的結果，可以總結出，基于K 均值聚類方法的冗余特征剔除方法，當采用SVM多分類器進行故障診斷時，診斷準確率優于PCA、LPP和PCA 方法，同時冗余特征剔除帶來的最直觀的性能提升是時間復雜度大大降低，但沒有影響診斷準確率，因此本文達到了平衡時間復雜度和診斷準確率之間的矛盾的目的。

5 結語

本文提出了一種基于優化K 均值聚類的冗余故障特征剔除方法，針對旋轉機械的軸承故障診斷，有效地解決了多維特征造成的時間復雜度高的問題，同時通過與其他常用三種方法比較發現，本文方法并沒有降低診斷準確率。通過對凱斯西儲大學軸承實驗室的測試數據進行實驗驗證，結果表明本文方法有效地改善了多維特征用于診斷時，時間復雜度和診斷準確率之間的矛盾，為信號處理技術更好的服務于機械故障診斷領域提供重要參考。