雙曲線中的六類易錯題型
■河南科技大學附屬高級中學 曲少寧
雙曲線是圓錐曲線的重要內容之一,也是高考必考內容。從近幾年高考情況來看,雙曲線的定義、標準方程、幾何性質一直是高考的熱點,但由于學生對概念或公式理解模糊,以及一些細節把握不準確,從而導致出現不同類型的錯誤。所以同學們在解題時,要密切注意一些易錯點,下面就同學們解題中易錯的類型進行簡要總結分析。
易錯點一:對定義理解不透徹,忽視雙曲線定義中的限制條件
例1已知兩圓C1:(x+5)2+y2=9,C2:(x-5)2+y2=9,動圓C與圓C1外切,且與圓C2內切,求動圓圓心C的軌跡方程。
錯解:設圓C的半徑為r,則由題意知|CC1|=r+3,|CC2|=r-3,|CC1|-|CC2|=6,故圓心C的軌跡是以C1,C2為左右焦點的雙曲線。
2a=6,a=3,c=5,b2=c2-a2=16,所以圓心C的軌跡方程是
錯解分析:忽視雙曲線定義中是差的絕對值,誤以為所求的軌跡是整個雙曲線。
正解:設圓C的半徑為r,則由題意知|CC1|=r+3,|CC2|=r-3,|CC1|-|CC2|=6,故圓心C的軌跡是以C1,C2為左右焦點的雙曲線的右支。 2a=6,a=3,c=5,b2=c2-a2=16,所以圓心C的軌跡方程是=1(x≥3)。
變式已知A(-3,0),B(3,0)。
(1)若|PA|-|PB|=6,則P點的軌跡_____;
(2)若|PA|-|PB|=8,則P點的軌跡_____;
(3)若|PA|-|PB|=4,則P點的軌跡____。
解析:(1)|PA|-|PB|=|AB|,由平面幾何知識可知,P點的軌跡是以B為端點的一條射線,點P的軌跡方程為y=0(x≥3)。
(2)|PA|-|PB|>|AB|,與三角形兩邊之差小于第三邊相矛盾,故軌跡不存在。
(3)因為|PA|-|PB|<|AB|,所以P點的軌跡是雙曲線的右支,其中A、B為左、右焦點, 2a=4,a=2,c=3,故P點軌跡方程為=1(x≥2)。
例2已知P是雙曲線=1 上一點,F1、F2是雙曲線的左、右焦點,且|PF1|=17,求|PF2|的值。
錯解:由雙曲線的定義可知,||PF1|-|PF2||=2a=16。因為|PF1|=17,所以|PF2|=1或|PF2|=33。
錯解分析:忽視了雙曲線上點的隱含條件。由|PF1|=17,可以確定點P在左支上,解得|PF2|=33。
正解:由雙曲線的定義可知, 若P在右支上,則|PF1|≥a+c=18。而已知|PF1|=17,故P在左支上。則|PF2|-|PF1|=2a=16,|PF2|=33。
易錯點二:忽視焦點的位置
例3求與雙曲線有公共漸近線,且過點M(2,-2)的雙曲線方程。
錯解:雙曲線的漸近線方程為y=,故所求雙曲線的漸近線方程也為y=。設所求雙曲線方程為=1(a>0,b>0),又,且M(2,-2)在雙曲線上,則=1,b2=-2,故不存在這樣的雙曲線。
錯解分析:雙曲線的焦點位置不確定,焦點可能在x軸上,也可能在y軸上。
正解:(解法一)雙曲線的漸近線方程為,故所求雙曲線的漸近線方程也為。若所求雙曲線的焦點在x軸,設所求雙曲線方程為1(a>0,b>0),又,且M(2,-2)在雙曲線上,則=1,b2=-2,焦點在x軸上不成立。若所求雙曲線的焦點在y軸上,設方程為=1(a>0,b>0),則。且過M(2,-2),解得a2=2,b2=4。所求雙曲線方程為
小結:與有公共漸近線的雙曲線系可以設為。
例4若方程表示雙曲線,求m的取值范圍。
錯解:因為=1表示雙曲線,所以3+2m>0且2+2m>0,解得m>-1。
錯解分析:焦點位置需討論。
正解:(解法一)若方程=1,若表示焦點在x軸的雙曲線,則3+2m>0且2+2m>0,解得m>-1;若表示焦點在y軸的雙曲線,則3+2m<0且2+2m<0得
所以m>-1或
易錯點三:在直線與雙曲線位置關系中,忽視了判別式這一前提條件
例5已知雙曲線,問過點P(1,1)能否作直線l,使l與雙曲線交于M,N兩點,且P為線段MN的中點。若存在,求出l的方程;若不存在,說明理由。
錯解:(解法一)設存在這樣的直線l,直線的斜率k存在,設M(x1,y1),N(x2,y2),雙曲線方程可化為2x2-y2=2,則= 2。兩個式子相減得2(x1-x2)·(x1+x2)-(y1-y2)(y1+y2)=0。P為線段MN的中點,則x1+x2=2,y1+y2=2,4(x1-x2)-2(y1-y2)=0,得k=2。所求直線方程為y-1=2(x-1),即2x-y-1=0。
(解法二)假設存在這樣的直線,顯然直線的斜率存在,假設直線的方程為y-1=k(x-1),即y=kx+1-k。代入雙曲線方程2x2-y2=2,化簡整理得(2-k2)x2-2k(1-k)x-(1-k)2-2=0。設M(x1,y1),N(x2,y2),則2-k2≠0且x1+x2=2。又x1+x2=,解得k=2。
所求直線方程為2x-y-1=0。
錯解分析:解法一,解法二都沒有驗證直線是否與曲線有兩個交點,而把所求直線與雙曲線聯立時發現得到的一元二次方程的判別式小于零,答案錯誤。
正解:(解法一)過程同錯解,得到2x-y-1=0,將y=2x-1 代 入2x2-y2=2 中,得到2x2-4x+3=0,Δ=b2-4ac=-8<0,所以不存在這樣的直線。
(解法二)過程同錯解,化簡整理得,
(2-k2)x2-2k(1-k)x-(1-k)2-2=0。
設M(x1,y1),N(x2,y2),因l與雙曲線交于M,N兩點,且P為線段MN的中點,故2-k2≠0,Δ>0,x1+x2=2。經計算k無解,故不存在這樣的直線。
小結:解決直線與雙曲線位置關系問題時,必須判斷直線與雙曲線的交點個數,一種方案是將計算結果代入,驗證判別式是否大于零,另外一種方案是聯立后先解Δ>0,從而找到限制條件。
易錯點四:焦點弦的弦長問題
例6過雙曲線x2-y2=1 的右焦點作直線交雙曲線于M,N兩點。
(1)若|MN|=2,則這樣的直線可作____條。
(2)若|MN|=3,則這樣的直線可作_____條。
錯解:(1)因為直線過右焦點,而通徑=2=|MN|,所以只有一條滿足題意。
錯解分析:在雙曲線中過焦點的所有弦中,誤以為通徑最短。實際上,過焦點且交于同一支的所有弦中通徑最短,而過焦點且交于兩支所有弦中最短的弦為實軸。
正解:(1)若直線與右支有兩個交點,由題意知通徑=2=|MN|,此時只有一條直線滿足條件;若直線與左右兩支各有一個交點,|MN|=2=2a,而2a為兩頂點間距離,故此時只有一條直線滿足條件。
所以當|MN|=2時,這樣的直線共有兩條。
所以當|MN|=3時,這樣的直線共有四條。
易錯點五:忽視二次項系數
例7直線l:y=k(x-1),雙曲線x2-y2=4,試討論實數k的取值范圍:
(1)直線l與雙曲線有兩個公共點;
(2)直線l與雙曲線有且只有一個公共點。
錯解:y=k(x-1)代入x2-y2=4得:
(1-k2)x2+2k2x-k2-4=0。
(1)直線l與雙曲線有兩個公共點,則:
(2)直線l與雙曲線有且只有一個公共點,則Δ=0,解得
錯解分析:聯立后的(1-k2)x2+2k2xk2-4=0式子中,二次項系數為1-k2可能為正,可能為負,也可能為零。
正解:y=k(x-1)代入x2-y2=4得:
(1-k2)x2+2k2x-k2-4=0。
(1)直線l與雙曲線有兩個公共點,則:
1-k2≠0,且Δ>0。
(2)直線l與雙曲線有且只有一個公共點,則①1-k2=0;②1-k2≠0且Δ=0。
解得k=±1或k=
易錯點六:忽視直線斜率不存在
例8已知雙曲線方程=1(a>0,b>0)的兩條漸近線方程分別為l1:y=2x,l2:y=-2x。
(1)求雙曲線方程E的離心率。
(2)O為坐標原點,動直線l分別交l1,l2于A,B兩點(A,B分別在第一、四象限),△ABO的面積恒為8,試探究是否存在總與直線l有且只有一個公共點的雙曲線E。若存在,求出雙曲線方程E的方程;若不存在,說明理由。
解析:(1)兩條漸近線方程分別為l1:y=2x,l2:y=-2x,所以。
設直線l方程為y=kx+m,依題意得k<-2或k>2。
聯立y=kx+m與y=2x,得y1=
由S=|OC|·|y1-y2|得=8,整理得m2=4|4-k2|=4(k2-4)。①
將y=kx+m代入=1中,得:
(4-k2)x2-2kmx-m2-4a2=0。
因雙曲線E與直線l有且只有一個公共點,且4-k2<0,故Δ=0。
(-2km)2-4(4-k2)(-m2-4a2)=0。
展開合并化簡得m2+4a2-a2k2=0。將①代入得,4k2-16+4a2-a2k2=0。
整理得(4-k2)(a2-4)=0,所以a2=4。
錯解分析:直線的斜率不一定存在,所以不能直接設直線方程y=kx+m,應該分為斜率存在與不存在這兩種情況討論。
正解:由(1)知雙曲線的方程為=1,設直線l與x軸交于C點。
當l⊥x軸,雙曲線E與直線l有且只有一個公共點,直線l過雙曲線的右頂點,此時l的方程為x=a, 則|OC|=a,|AB|=4a。因△ABO的面積恒為8,所以|OC|·|AB|=8,解得a=2。
當l不與x垂直,同錯解部分。
綜上所述,總存在與直線l有且只有一個公共點的雙曲線E,且雙曲線E方程為=1。
練習題:
1.在△ABC中已知|AB|=4,2sinA-2sinB=sinC,建立適當的坐標系,求頂點C的軌跡方程。
解析:以AB所在直線為x軸,AB中垂線為y軸,建立直角坐標系。因為|CB|-|CA|=,所以點C的軌跡為雙曲線的右支。則A(-2,0),B(2,0),設C(x,y)(x>1)。
由2sinA-2sinB=sinC得,|CB|-|CA|=,所以C的軌跡方程為x2-=1(x>1)。
2.已知雙曲線的一條漸近線方程為2x-3y=0,且焦距為,求雙曲線的標準方程。
解析:一條漸近線方程為y=,若焦點在x軸上,設所求雙曲線方程為1,且。又c= 13,解得=1。若焦點在y軸上,設所求雙曲線方程為=1,且。又c= 13,解得=1。
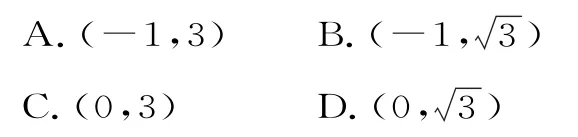
解析:若表示焦點在x軸上的雙曲線,則a2=m2+n,b2=3m2-n。又c=2,a2+b2=c2,解得m2=1。又由m2+n>0且3m2-n>0,可得-1<n<3。
若表示焦點在y軸上的雙曲線,則= 1,化為=1。則a2=n-3m2,b2=-m2-n。又由c=2,a2+b2=c2,解得m2=-1(舍去)。
故選A。

