淬火動力學中的拓撲不變量*

楊超 陳澍

1) (中國科學院物理研究所,北京凝聚態物理國家研究中心,北京 100190)

2) (中國科學院大學,物理科學學院,北京 100049)

3) (長三角物理研究中心,溧陽 213300)

本文主要介紹了近期關于一維拓撲能帶系統中淬火動力學的研究.從兩能帶模型入手介紹了動力學陳數,并給出它與初末態拓撲不變量之間的關系.進而通過將一維含時波函數看作為1+1維母哈密頓量的基態,給出了Altland-Zirnbauer分類對應的動力學拓撲分類,并簡要介紹了動力學的體邊對應以及空間無序和能帶色散對糾纏譜交叉的影響.最后還介紹了利用超導量子比特模擬觀測到動力學陳數.

1 引 言

1980年整數量子霍爾效應的發現開啟了拓撲量子物態研究的大門[1,2].不同于傳統的量子物態,拓撲物態不存在局域的序參量,而是由波函數的幾何或拓撲性質決定,且可以用拓撲不變量來描述.在有能隙的系統中,人們對于拓撲能帶系統的分類和性質的研究已經有了系統的方法和深刻的認識[3,4,5].然而目前關于拓撲物態的研究大都集中在研究系統基態波函數的性質,對于遠離平衡態過程的拓撲性質的認識還非常不足.近年來,由于冷原子技術的迅速發展,已經能夠模擬許多重要的拓撲模型,如一維Su-Schrieffer-Heeger(SSH)模型[6-11],這為進一步探索它們的非平衡性質提供了有力的工具.

一類典型的遠離平衡態的過程就是淬火動力學.在 t ≤ 0 時 系統的波函數 | Ψi〉 處 于哈密頓量Hi的基態,在 t=0 時刻突然改變哈密頓量的某些參數,即淬火,這樣初態波函數按照新哈密頓量 Hf做幺正演化.這里有兩點需要特別指出: 首先,淬火過程分為局域的淬火和全局的淬火,對局域的淬火,系統參數的改變局限在有限的尺度內,而對全局的淬火,哈密頓量的參數在整個系統內都發生了改變,本文中僅研究全局淬火;其次,淬火前后哈密頓量的性質原則上沒有任何約束,作為一種最簡單的特例,我們要求初末態哈密頓量具有相同的對稱性.在這些限制下,我們關心在波函數 | Ψ (t)〉 中是否有拓撲性質的體現.

對波函數 | Ψ (t)〉 拓撲性質的研究仍然有三種不同的方法.第一種直觀的思路是研究在每一個固定時刻t波函數本身的拓撲性質.這也是到目前為止最常用的方法.例如,在陳絕緣體中,系統的陳數在淬火后會保持不變,這也被稱為NO-GO定理[12,13].從一個平庸的態出發,可以制備出的量子態能多接近于拓撲非平庸的態[14,15].最近Cooper等還證明了在淬火動力學過程中只有幺正對稱性會被保持,反幺正的對稱性會在含時演化中被破壞,這被稱作動力學誘導的對稱性破缺[16].進一步,當只考慮幺正對稱性時,我們可以研究系統在每個時刻t的拓撲性質并可以給出拓撲分類[16,17].第二種方法是將時間和空間放在一起研究 (D+1) 維波函數的拓撲性質.在研究二維陳絕緣體中的淬火動力學時,翟薈研究組首先注意到這個動力學過程可以看作(kx,ky,t)到Bloch球上的映射,它可以由Hopf不變量或連環數描述,并且若初態為拓撲平庸態,Hopf不變量就等于演化哈密頓量 Hf的陳數[18,19],緊接著Weitenberg等通過在實驗中觀測到了動力學渦旋與靜態渦旋的連環數[20].我們研究組系統地研究了一維拓撲系統的淬火動力學,定義了動力學陳數,并指出動力學陳數與初末態哈密頓量拓撲不變量之間的關系[21],隨后同實驗組合作在超導量子比特模擬實驗中觀測到了動力學陳數和動力學量子相變的特征[22].另外,Ueda研究組利用K理論也給出了 (1+1) 維系統的拓撲分類和動力學實現.并且指出當初態為拓撲平庸態時,這個動力學拓撲不變量意味著糾纏譜的演化在某些時刻會有交叉,這可以看作動力學的體邊對應[23].第三種方法是研究布里淵區中的能帶反轉面(BIS),通常它為 (D-1) 維,劉雄軍研究組注意到初態為拓撲平庸態時,演化哈密頓量 Hf的拓撲性質由在能帶反轉面上定義的纏繞數得到[24-26],并在冷原子實驗中被觀測到[27].

這三種方法從不同的角度給出了初態波函數|Ψi〉在含時演化時的性質,盡管它們之間存在一些關聯,但它們并不等價.另外需要指出,在研究系統拓撲性質時需要要求哈密頓量是局域的,但在時間演化過程中,系統的關聯不斷傳播,等效哈密頓量將不再局域,因此我們要求時間尺度小于 L/vLR,其中 vLR是 Lieb-Robinson 速度[28,29].在這篇綜述中,我們主要利用第二種方法討論 (1+1) 維系統的拓撲性質.

本文首先從兩能帶模型入手,介紹淬火動力學過程中動量時間流形的結構,定義了動力學陳數,并指出動力學陳數與初末態拓撲數之間的關系.接著給出更普遍情況下(1+1)維系統的動力學拓撲分類和體邊對應,即糾纏譜演化過程中出現的交叉,接著簡要分析糾纏譜交叉受空間無序和能帶色散的影響.最后介紹利用單量子比特模擬淬火動力過程,直觀看到動力學陳數的幾何意義.

2 一維二能帶系統中的動力學拓撲不變量

我們首先以一維二能帶系統為例,討論它的動力學拓撲不變量.動量空間中的哈密頓量可寫為

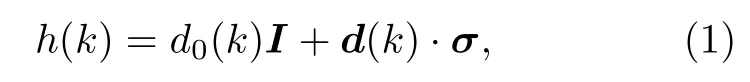
其中泡利矩陣 σ 作用在 (贗) 自旋 1/2 的空間,其本征值為 E±(k)=d0(k)±|d(k)|,對應的本征態記為|ψ±(k)〉,因此密度矩陣可表示為

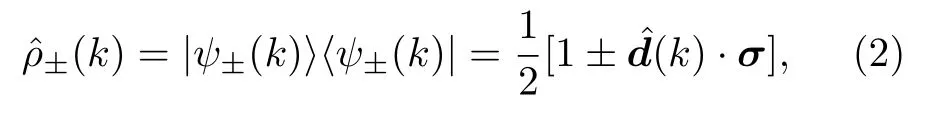
如果將t時刻的密度矩陣寫為

對于平帶化的哈密頓量,不同的動量模式具有相同的周期 π/|df|,動量時間流形為 T2=S1×S1,如圖1(a)所示.更進一步,如果動量空間中存在一些不動點滿足di(kc)和df(kc)共線,對于這些kc,Bloch矢量除了一個整體的相位將不會演化,因此將這些kc稱為不動點.如圖1(b)所示的k1和k2.在這些不動點上,時間軸可以連續的收縮為一點,將動量時間流形約化為了一系列的球面 S2.如果布里淵區內有N個不動點,則動量時間流形將約化為N個球面.在每一個球面上,密度矩陣可以看作從動量空間子流形 S2到Bloch球的映射,因此我們可以定義動力學陳數

圖1 (a) 每個截面對應固定動量,截面內的極角對應于時間.橘黃色的環代表 k=0 和 2π,它們粘合起來組成了T2;(b) 如果動量空間中存在一些不動點 k1,k2,截面的時間可連續收縮為一個點,動量時間流形約化成一系列球面[21]Fig.1.(a) For any fixed momentum k,the cross section can be viewed as a circle S1 where the azimuthal angle represents the time t.After gluing k=0 and k=2π (saffron circles),the topology of the momentum-time manifold becomes T2 ;(b) if there are two fixed points k=k1 and k2,the corresponding circle contracts to a point,then the momentum-time manifold reduces to a series of spheres S2[21].

其中 km表 示第m個不動點而 m=1,2,···,N,直接計算得到

根據Altland-Zirnbauer分類,一維二能帶系統拓撲非平庸類有 BDI,AIII和 D.其中 BDI和AIII類具有手征對稱性,對于 BDI和 AIII類,不動點的個數存在下限 2 |ni-nf|,相應的非平庸陳數的個數 M也存在下限 2 |ni-nf|,其中 ni和nf分別是初末態哈密頓量 hi和hf的纏繞數,由于靜態哈密頓量的拓撲分類為 Z,因此由 2 |ni-nf| 決定的動力學拓撲分類也是 Z.而D類的具有粒子空穴對稱性系統的不動點為 k=0 和k=π[33],因此對稱性保

護的不動點個數為 2 |ni-nf|,此時 ni,nf∈{0,1} 是系統的 Z2不變量,因此由 2 |ni-nf| 決定的動力學拓撲分類也是 Z2.特別的,由于系統所有動力學陳數之和為 0,我們僅需考慮子流形(k,t)∈(0,π)× (0,π/|df|)對 應的動力學陳數則可以證明若 hi和hf位 于同一個相,動力學陳數若位 于不同 的相,動力學陳數綜上所述,對 BDI、AIII和 D 類,非平庸動力學陳數的個數均只依賴于初末態哈密頓量拓撲數之差.

現在,我們以兩個例子展示動力學陳數.首先我們考慮SSH模型[34],dx=(1+δ)+(1- δ)cosk,dy=(1-δ)sink,其中 δ ＜0 時系統的基態是拓撲非平庸的,而 δ ＞0 時基態是拓撲平庸的.哈密頓量具有時間反演對稱性 K h(k)K=h(-k) 和手征對稱性 σzh(k)σ=-h(k),屬于 BDI類.容易看出對于任意的初末態 δi和δf,系統只有兩個不動點k=0和k=π.布里淵區被分為 k ∈ (0,π) 和k ∈ (π,2π).若 δi和δf同號,Bloch矢量滿足和跟據 (7)式有動力學 Chern數為非平庸的 Chern數個數為0=2|ni-nf|.另一方面,若 δi和δf異號,Bloch 矢量滿足動力學 Chern 數為非平庸Chern數的個數為2=2|ni-nf|.我們在考慮推廣的p波超導模型[33,35],dx=Δ2sinφsin2k,dy=Δ1sink+Δ2cosφsin2k,dz=-t1cosk-t2cos2k+μ,此處 t1(t2)和Δ1(Δ2eiφ)分別是最(次)近鄰格點的躍遷強度和p波配對強度,μ 是化學勢,次近鄰躍遷帶有的相位破壞了系統的時間反演對稱性.為了方便我們取 Δ1=t1=0.5,Δ2=t2≡ Δ,φ=π/2以及μ=1.此時若0.5＜Δ＜1.5 時,基態是拓撲超導態;若 Δ ＜0.5 或Δ＞1.5時,基態是普通超導態.容易看出Bloch矢量在不動點滿足和利用 (7)式容易驗證當初末態在同一個相時而初末態處在不同相時

3 (1+1)維系統的動力學拓撲分類

在第2節中我們直觀的討論了一維二能帶系統的動力學拓撲不變量,這一節中,我們用更一般的方法計算 (1+1) 維系統的動力學拓撲分類.我們記初末態平帶化的哈密頓量為滿足hi2(k)=hf2(k)=1,于是可以定義母哈密頓量

系統的波函數 | ψ (k,t)〉 是母哈密頓量的瞬時本征態,化學勢位于 μ=0.由矩陣指數公式直接計算得到[23]可以看出平帶化的母哈密頓量滿足特別的,對二能帶系統,母哈密頓量為即 (5) 式.

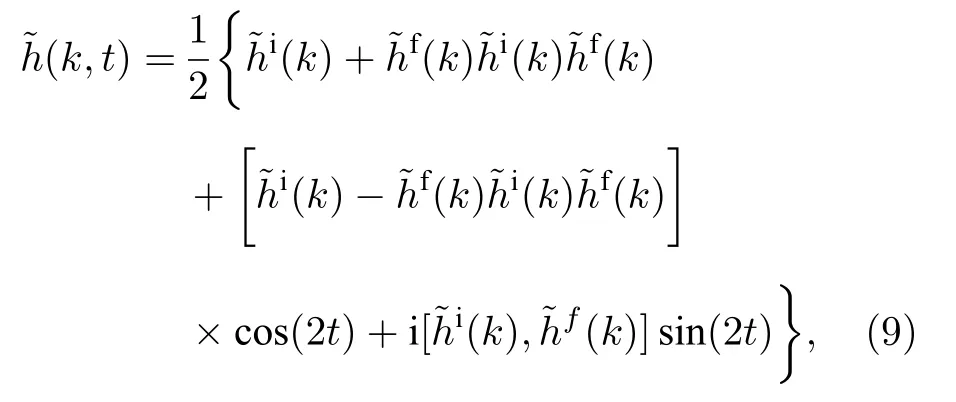
進一步利用(9)式,我們從平衡態哈密頓量的對稱性得到 (1+1) 維母哈密頓量的對稱性

這里我們直接將對稱性算符記號T,C和Γ 用在了母哈密頓量中,而將時間看作額外維度的準動量,然而它們并不是真正的時間反演對稱性,粒子空穴對稱性和手征對稱性的.根據文獻[16]中可知只有粒子空穴對稱性在含時演化中會保持,時間反演對稱性和手征對稱性都將被破壞.根據文獻[36,37,23]中的方法,母哈密頓量的拓撲分類可利用K群得到,如表1所示.可以看出 A、AI和AII類中母哈密頓量的對稱性與AZ分類相同,具有相同的拓撲不變量.

盡管我們得到了母哈密頓量的拓撲分類,但對于淬火動力學過程,只有部分拓撲等價類能夠實現.對于 A類,系統的拓撲不變量為陳數,利用(9)式可得系統的陳數為 0,因此動力學分類為Z→0.對于 AIII類,系統在高對稱點 ts=0,π 滿足因此可以定義纏繞數 n=根據文獻 [38],系統的拓撲不變量分別為陳數和高對稱點處纏繞數之差,因此動力學分類為利用(9)式可得

其中 ni和nf是初末態哈密頓量的纏繞數.特別的,若系統只有兩個能帶,這里的兩個獨立的拓撲數分別分別對應上一節中的動力學陳數之和與非平庸動力學陳數個數的下限.類似的,對于BDI和CII類,時間反演對稱性保證系統陳數為0[23],動力學分類即K群 Z →Z,系統的拓撲不變量為高對稱點處纏繞數之差,即 (11)式.對于 AII類,系統拓撲不變量為 Fu-Kane不 變量[39],Moore和Balents提出它等價于三部分陳數之和是半布里淵區上的陳數,而 CL和CR分 別是將的兩個邊界收縮為一點時補上的陳數.利用(9)式可直接求得系統總的動力學陳數是拓撲平庸的,即動力學分類為 Z2→0.類似地,對于D類可以得到總的陳數

表1 母哈密頓量 的拓撲分類.TRS、PHS、CS 分別是時間反演對稱性,粒子空穴對稱性和手征對稱性.s,t,d,d,額外對稱性P參見文獻[37];original class是沒有額外對稱性時系統的拓撲分類.是系統的K群.//Dynamical realization表示在淬火動力學中存在的拓撲分類.Stable against dispersion指能帶存在色散時糾纏譜交叉能夠穩定存在的拓撲分類Table 1.Topological classification of parent Hamiltonian.TRS,PHS and CS represent the time reversal symmetry,particle hole symmetry and chorial symmetry,respectively.The definition of s,t,d,d//and additional symmetry P can be found in Ref.[37].Original class represents the topological classification without additional symmetry. is the K group.Dynamical realization means the topological classes which can be realized in quench dynamics.Stable against dispersion means entanglement spectrum crossing which is stable against band dispersion.

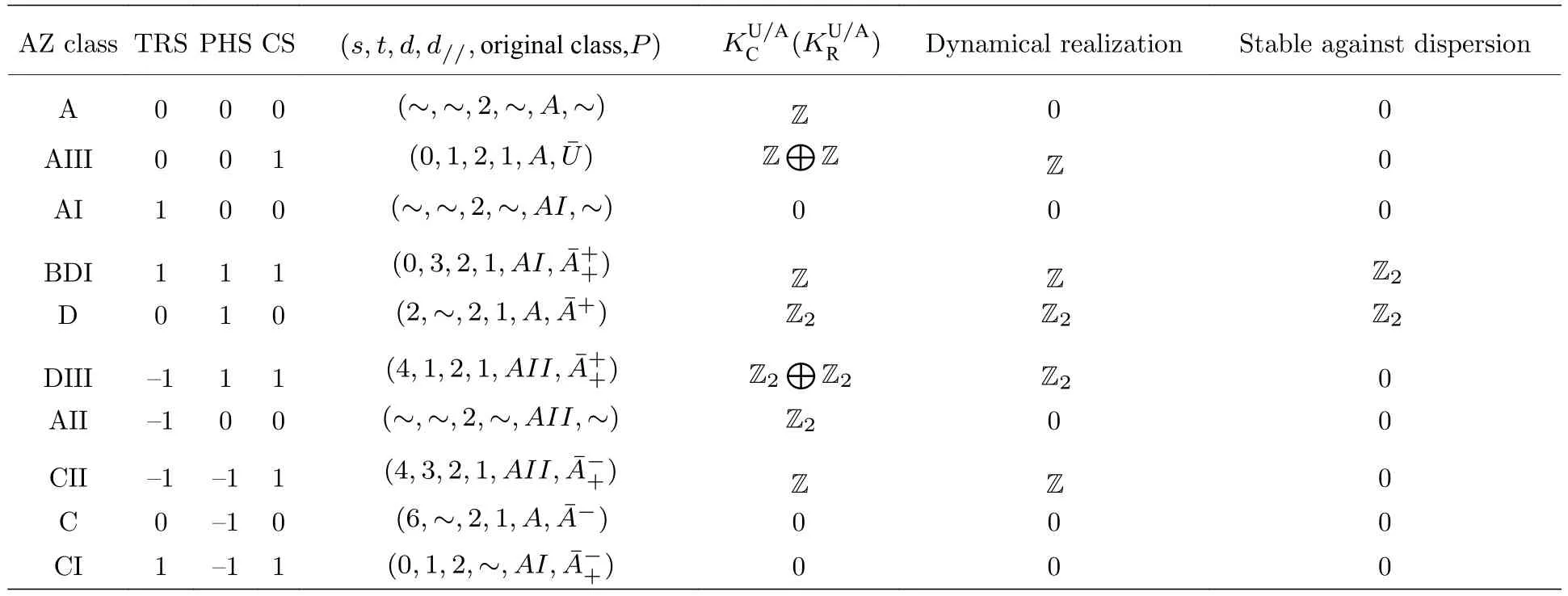
表1 母哈密頓量 的拓撲分類.TRS、PHS、CS 分別是時間反演對稱性,粒子空穴對稱性和手征對稱性.s,t,d,d,額外對稱性P參見文獻[37];original class是沒有額外對稱性時系統的拓撲分類.是系統的K群.//Dynamical realization表示在淬火動力學中存在的拓撲分類.Stable against dispersion指能帶存在色散時糾纏譜交叉能夠穩定存在的拓撲分類Table 1.Topological classification of parent Hamiltonian.TRS,PHS and CS represent the time reversal symmetry,particle hole symmetry and chorial symmetry,respectively.The definition of s,t,d,d//and additional symmetry P can be found in Ref.[37].Original class represents the topological classification without additional symmetry. is the K group.Dynamical realization means the topological classes which can be realized in quench dynamics.Stable against dispersion means entanglement spectrum crossing which is stable against band dispersion.

AZ classTRSPHSCS (s,t,d,d//,originalclass,P)Dynamical realization Stable against dispersion A 0 0 0 (～,～,2,～,A,～)KU/A C (KU/AR )Z⊕Z Z 0 0 AIII001(0,1,2,1,A,ˉU)Z 0 AI 1 0 0 (～,～,2,～,AI,～)000 BDI111(0,3,2,1,AI,ˉA++)Z2 D010(2,～,2,1,A,ˉA+)Z Z Z2Z2Z2 DIII—111(4,1,2,1,AII,ˉA++)Z2⊕Z2Z20 AII —1 0 0 (～,～,2,～,AII,～)Z200 CII—1—11(4,3,2,1,AII,ˉA-+)Z Z 0 C0—10(6,～,2,1,A,ˉA-)000 CI1—11(0,1,2,～,AI,ˉA-+)000

4 動力學體邊對應與無序

平衡態哈密頓量存在體邊對應,體態的拓撲性質在開邊界下等于邊界態的個數[41].對于平帶化的哈密頓量,開邊界下系統的能譜也是基態的單粒子糾纏譜[42],因此我們通過系統糾纏譜的演化來研究動力學體邊對應.對于費米子二次型 H=其中 i,j 是格點指標,系統的基態記為我們將系統分為子系統A和環境B,則子系統的約化密度矩陣為其中糾纏哈密頓量 HA仍為費米子二次型,它的本征值記作 εn.此外我們將子系統關聯矩陣的 本征值 ξn定義為單粒子糾纏譜,則有

在淬火動力學演化的過程中,系統波函數仍然是高斯態,因此瞬時波函數的單粒子糾纏譜可以寫為:

其中糾纏譜ξn(t)是瞬時關聯矩陣Cij(t)=的本征值,εn(t)是瞬時糾纏哈密頓量的本征值.容易看出糾纏哈密頓量若存在零模εn(t)=0,則糾纏譜存在模ξn(t)=1/2.有了單粒子糾纏譜進而可以得到多體糾纏譜為[42]

從此式可以看出糾纏哈密頓量的零模意味著多體糾纏譜的簡并.

下面我們以SSH模型為例,初態 δi=1 為拓撲平庸的,δf取不同值時糾纏譜的演化見圖2(a).從圖中看出,若末態也是拓撲平庸的,糾纏譜在含時演化過程中能隙始終打開,然而若末態哈密頓量是拓撲非平庸的,則糾纏譜會在某時刻發生交叉,此時在系統虛擬的邊界會存在糾纏哈密頓量的邊界態.對于拓撲超導系統,糾纏譜的交叉意味著子系統宇稱發生了改變,整個周期內有奇數個電子從子系統流向外部[45,46].為了確定系統的動力學拓撲分類,我們可以考慮多條鏈的耦合.我們用平帶化的末態哈密頓量進行時間演化,對于 Z 類系統,糾纏譜交叉時刻的簡并度正比于鏈數,而對于 Z2類系統,糾纏譜是否會出現交叉僅僅依賴與鏈數目的奇偶性[23].

我們知道對于平衡態拓撲系統,若在實空間中加入弱的無序時,只要不破壞系統的對稱性則其邊緣模依舊存在.在淬火動力學中,無序既可以出現在實空間,也可以出現在頻率空間,末態哈密頓量的色散即可看成一種頻率空間的無序[23].特別地,如果系統的能帶具有色散,對稱性關系(10)式不再成立,根據文獻[16],只有反幺正對稱性才能在含時演化中繼續存在,幺正對稱性在含時演化中將被破壞,這也被稱作動力學誘導的對稱性破缺,因此只有粒子空穴對稱性在含時演化中能夠保持.進一步由于我們考慮的是糾纏的邊界態,能帶色散使得時間反演對稱性和手征對稱性在邊界處無法保持對稱性,系統的動力學對稱性被破壞.這類似于空間群對稱性保護的拓撲態中體邊對應的破缺[5,47,48].于是AIII類和CII類的動力學拓撲性質不能在能帶有色散時穩定存在;D類的拓撲性質不受能帶色散影響;對于BDI類,能譜的色散使得高對稱線t=0 和t=π 變得動量依賴,兩條高對稱線可以連續形變,這使得高對稱線上纏繞數之差允許模2改變,從而系統穩定的動力學分類為 Z →Z2;最后DIII類通過數值驗證能帶色散會導致糾纏譜能隙打開,穩定的動力學分類為 Z2→0.最后我們以AIII類為例展示了能帶色散對糾纏譜能隙的影響.我們將SSH模型加上次次近鄰躍遷[46],哈密頓量 為 dx=(t0+δ)+(t0- δ)cosk+Jcos(2k+φ),dy=(t0- δ)sink+Jsin(2k+φ).為了方便我們固定 t0=0.75,J=0.2 和φ=0.5π,初態取為δi=0.25,基態是拓撲平庸的,末態取 δf=-0.25,基態是拓撲非平庸的.糾纏譜的演化如圖2(b)所示,可以看出能帶的色散打開了糾纏譜的能隙,動力學拓撲性質不再存在.

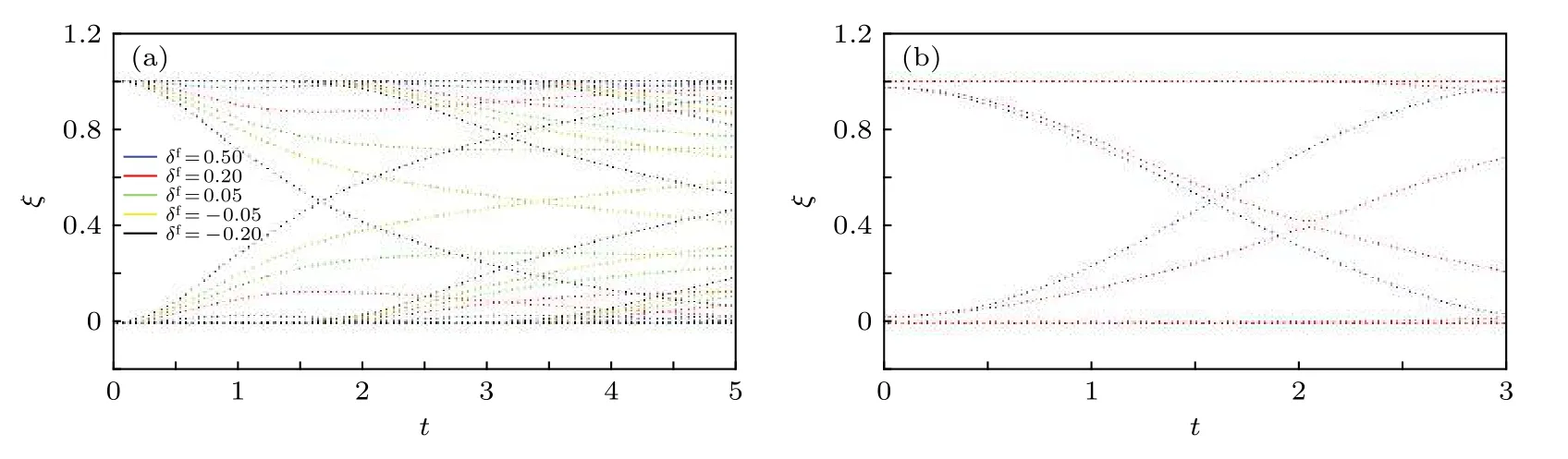
圖2 (a) SSH 模型,初態 δi=1 為 拓撲平庸的,末態 δf 取不同的值.僅當末態為拓撲非平庸時,糾纏譜在 1/2 處有交叉;(b) 擴展的SSH模型,次次次近鄰躍遷具有相位,系統屬于AIII類.藍色的線代表用平帶化的哈密頓量進行動力學演化,紅色的線代表由真實末態哈密頓量進行演化.可以看出能帶的色散打開了糾纏譜的能隙Fig.2.(a) In SSH model,the initial state of δi=1 is topologically trivial,evolution of entanglement spectrum for different postquenched δfs are shown with different colors.If and only if the post-quenched Hamiltonian is topologically nontrivial,the entanglement spectrum can cross at 1/2 ;(b) in Extended SSH model,the third-nearest-neighbor hopping carries a phase factor,and the Hamiltonian belongs to class AIII.The blue curve shows the dynamics of entanglement spectrum evolved by flattened Hamiltonian,and the red curve shows the dynamics evolved by entanglement spectrum of real Hamiltonian.It can be seen that the band dispersion opens the gap of entanglement spectrum.

5 實驗測量

超導Xmon量子比特是研究量子模擬和量子計算的一個非常有前景的實驗平臺[49-51],這一小節簡要介紹由單量子比特模擬淬火動力學的過程[22].對于每個固定的動量k,通過外加脈沖制備出初態哈密頓量的基態,在時間t改變外加脈沖實現淬火過程,如圖3(a)所示,通過態層析測量可以得到Bloch矢量的演化[52].實驗中布里淵區取了 30 個點,相當于系統尺寸 L=30,一個時間周期內有70離散的步長,每個步長為 15 ns,因此整個周期的演化時間為 1 .05 μs,每一次態層析測量是 5 000 次測量的平均.系統能量的弛豫時間為 T1=8.3 μs,失相時間為 T2?=6.8 μs,spin echo 的失相時間為T2se=11.7μs.

圖3 (a) 實驗過程序列示意圖.對每一個動量 k,初始時刻通過脈沖 A0cos(ωt+φ0) 制備初態,而后通過改變外加的脈沖的 A k和φk 實現淬火動力學.(b),(c) 不同動量 k 對應的Bloch矢量的演化.紅色的星為實驗的數據,黃色的環為數值計算的數據.(b)初 態 hi=0.2,末 態 hf=1.5.(c)初態 hi=0.2,末態 hf=0.5[22]Fig.3.The scheme of experiment control sequence.The initial state is prepared at the state-initialization period by control quantity A0cos(ωt+φ0) for a fixed momentum k.Then for a quantum quench,by controlling A k and φk,we adjust the direction of the rotation axis.(b),(c) the evolution of Bloch vectors for different momenta.The red points and yellow rings are experimental and numerical datas.(b)pre-quenched parameter hi=0.2,post-quench parameter hf=1.5.(c) pre-quenched parameter hi=0.2,postquench parameter hf=0.5.

實驗模擬的為橫場伊辛模型,通過Jordan-Wigner變換后它等效于Kitaev提出的p波超導鏈,哈密頓量為 dx=0,dy=sink,dz=Jz-cosk[53],其中若 Jz＜1 基態為鐵磁相或拓撲超導相,若Jz＞1基態為順磁相或普通超導相.通過Jordan-Wigner變換,我們將伊辛模型映射為一系列二能級系統,而對于每個由動量k標記的二能級系統我們可以利用單量子比特模擬其動力學演化.容易看出系統的不動點為 k=0 和k=π.我們始終取初態圖3(b)和圖3(c)分別展示了在半布里淵區中Bloch矢量的演化.可以看出當初末態哈密頓量在同一個相時,Bloch球被完整覆蓋,動力學陳數而初末態哈密頓量在同一個相時,Bloch球上的軌跡互相抵消,動力學陳數

6 總結與展望

本文主要介紹了一維對稱性保護的拓撲態的淬火動力學.首先以兩帶系統為例,從直觀上定義了動力學陳數,并給出了動力學陳數與初末態哈密頓量拓撲數之間的關系.然后通過分析 (1+1)-維母哈密頓量的拓撲性質給出了一般情況下系統的動力學拓撲分類和拓撲不變量.此外利用糾纏譜的動力學演化介紹了動力學的體邊對應,并分析了實空間和頻率空間無序對糾纏譜交叉的影響.最后介紹了利用了單量子比特模擬系統的動力學演化,通過測量Bloch矢量的演化直觀的展示了平庸和非平庸的動力學陳數.

此外,除了在一維系統,淬火動力學中的拓撲不變量在二維和高維系統[18,19,54,55],非厄米系統[56-58]等也有許多研究,但尚沒有完整成熟的理論.并且,如何在相互作用系統中定義動力學的拓撲不變量也尚未可知.在相互作用系統中單粒子關聯矩陣和糾纏哈密頓量并沒有這簡單的關系,只能直接求解系統的多體糾纏譜的演化.得益于冷原子,原子模擬,超導量子比特模擬等技術的迅速發展,淬火動力學的研究有了更好的實驗平臺,使得我們能更加深刻的理解拓撲系統的動力學性質.