憶容器多諧振蕩器及其實驗*

顧梅園 劉敬彪 王光義 梁燕 李付鵬

1) (杭州電子科技大學電子信息學院,杭州 310018)

2) (杭州電子科技大學機械工程學院,杭州 310018)

憶容器是一種具有記憶性的非線性電容,為研究憶容器的電路特性,提出了一種壓控型憶容器的二次曲線模型,利用電流反饋型運放等器件構建了能夠動態模擬憶容器q-v特性的仿真器.通過仿真和實驗觀測到憶容器的滯回曲線,以及隨外加激勵頻率增加而收縮的特性.分析了周期性激勵信號的參數對憶容值取值范圍的影響,并對憶容器的非易失性和平衡點的穩定性進行了研究.基于該憶容仿真器設計了一種多諧振蕩器,分析了振蕩器的工作原理,對振蕩器的輸出電壓、憶容器的端電壓、憶容器的磁通和電荷,以及憶容器的滯回曲線進行了測試.通過實驗中觀測到的各種振蕩波形,分析了振蕩器的頻率、占空比以及憶容器的非線性特性隨電路參數變化的規律.

1 引 言

2009年,Di Ventra 等[1]將憶阻系統的概念推廣到憶容系統,提出了憶容器的概念.憶容器是一種具有記憶性的非線性電容器,其本構關系滿足q—v平面上的緊致滯回曲線,憶容器在構造混沌電路、制備非易失性存儲器、低功耗計算、振蕩器和濾波器等領域具有潛在的應用價值[2-5].文獻[6]中介紹了由憶阻器和傳統的金屬-絕緣體-金屬電容器所構成的固態憶容器的實現方法.文獻[7]中報道了Pt-Fe2O3核殼納米粒子在P+-Si襯底上具有模擬憶容開關的特性.這些已報道的具有憶容效應的電子器件,由于成本和技術等方面的原因尚未被市場化.不少文獻在無法獲取實際憶容器的情況下,建立了憶容器的數學模型和電路模型,并進行了理論和應用研究.

文獻[8]中提出了一種憶容器的光滑曲線模型,并針對該模型設計了等效電路,但是該電路只體現憶容器狀態變量之間的數學關系,不能將憶容器作為一個二端元件進行電路的連接和測試.文獻[9]中針對在文獻[10]中提出的帶窗函數的荷控憶容器模型,研究了兩個憶容器的串并聯特性,并推導了瞬時等效記憶電容的解析表達式.Biolek等[11]利用端口變量的線性變換關系,提出了將憶阻器轉換為憶容器和憶感器的思路,并利用受控源分別設計和實現了荷控和磁控兩種憶阻器模型下的憶容仿真器.文獻[12]中利用模擬器件設計了憶阻仿真器,再利用AD844芯片將其轉換為憶容仿真器.該仿真器內部電路的輸出端由于不能短路接地,故工作條件受到浮地限制.文獻[13]中提出了一種憶阻器、憶容器和憶感器的通用緊湊型轉換器,并通過理論分析和電路實驗驗證了這些記憶元件的電氣特性.

隨著憶容器建模及特性分析的進展,更多的研究著眼于實際應用.文獻[5]中設計了一種包含憶阻器和憶容器的低通濾波電路,推導了該電路的傳遞函數,并測試了其頻率特性.文獻[8]中將憶容器模型應用到混沌振蕩電路中,發現該系統具有共存和對稱分叉的性質,并對其平衡點集、李雅普諾夫指數和吸引盆等非線性動力學特性進行了仿真和分析.文獻[14]中利用兩個憶容器的磁通耦合關系實現了一種振蕩頻率和占空比均可控的多諧振蕩器,但是該電路結構較復雜,且耦合效應對占空比調節的作用范圍較窄.文獻[15]中提出了一種通用的記憶器件模擬器,并將該模擬器分別替代RLC電路中的動態元件,對電路發生串聯諧振時動態元件的電壓波形和諧振曲線進行了仿真和測試.

已報道的文獻大多致力于憶容器模型的建立和仿真器的設計,對憶容器的應用研究尤其是將憶容器應用于多諧振蕩器的研究報道相對較少.本文提出了一種憶容器的二次曲線模型,并利用電流反饋型運放和乘法器等器件設計了憶容仿真器.仿真了憶容器在不同頻率的周期信號激勵下的滯回曲線,以及在周期信號激勵下憶容值Cm和磁通量φ的時域波形.研究了滯回曲線對頻率的依賴性,分析了激勵信號的參數對憶容值變化范圍的影響.通過繪制憶容器的dφ/dt-φ的動態路徑圖,研究了憶容器的非易失性和平衡點的穩定性[16,17],以及憶容器在不同記憶狀態間的切換方法和規律[18].將憶容仿真器應用到多諧振蕩器中,推導了振蕩器的狀態方程,并對振蕩器的工作原理進行了分析.最后通過實驗測試了憶容多諧振蕩器中各節點電壓的波形和憶容器的滯回曲線,研究并分析了三組電路參數對振蕩周期T、振蕩頻率f、占空比D,以及憶容器的非線性特性所產生的影響,提出了拓寬占空比調節范圍的解決方案.

本文設計的多諧振蕩器電路結構簡單,占空比和振蕩頻率調節范圍較寬,能夠提供多樣化穩定的矩形波信號,可應用于信號測試或設備驅動.

2 憶容器的數學建模

一個n階壓控型憶容器可以描述為[1]:

其中,q (t)是憶容器的電荷,vC(t) 是憶容器兩端的電壓,x 是憶容器的狀態變量,C (x,vC,t)為t時刻的憶容值,該值依賴于憶容器的內部狀態變量x和電壓 vC.類似地,一個n階荷控型憶容器可以描述為:

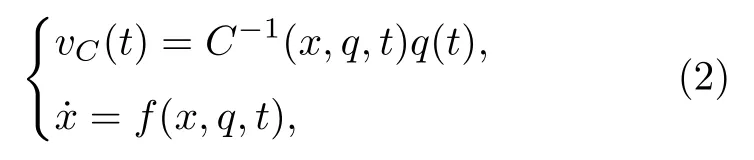
其中,C-1(x,q,t) 為 t時刻憶容值的倒數,該值依賴于憶容器的內部狀態變量x和電荷q.

本文提出了一種壓控型憶容器的二次曲線模型,其本構關系和狀態方程為

其中,憶容值 Cm(φ)=αφ2+β,φ 是憶容器的磁通量,α和β均為實常數,其典型參數 α=5.60×10-5,β=1.58×10-7.在壓控型憶容器兩端施加振幅為2 V,頻率為 f的正弦信號,繪制憶容器隨頻率變化的q-v特性曲線.如圖1所示,其q-v 特性曲線是一個在零點自交叉且奇對稱的緊致滯回曲線,它的滯回環面積隨外加正弦激勵頻率的增大而減小.當頻率增大到一定程度時,憶容器的 q-v特性曲線將退化為線性關系,憶容器近似為線性電容.

圖1 憶容器的 q-v 特性曲線Fig.1.q-v pinched hysteresis loops of memcapacitor.

假設憶容器的外加激勵為 vC(t)=Vmsin(2πft),因故可轉換為

由(4)式可知,在正弦交流電 vC(t) 的激勵下,憶容值Cm(t)的取值范圍為在 α 、β固定時,通過增大 Vm或減小f均可以拓寬憶容值Cm(t)的變化范圍,從而提高憶容器的非線性程度.假設憶容器的激勵 vC(t) 是振幅為 2 V、頻率為10 Hz 的正弦電 壓,憶容值 Cm(t)和磁通量φ (t) 的時域波形如圖2 所示.Cm(t) 是一個頻率為 20 Hz、的 正弦函數.當外加電壓vC(t)的瞬時值達到峰值時,Cm(t) 為最小值 158 nF.當外加電壓 vC(t) 的 瞬時值為零時,Cm(t) 為最大值214.8 nF.

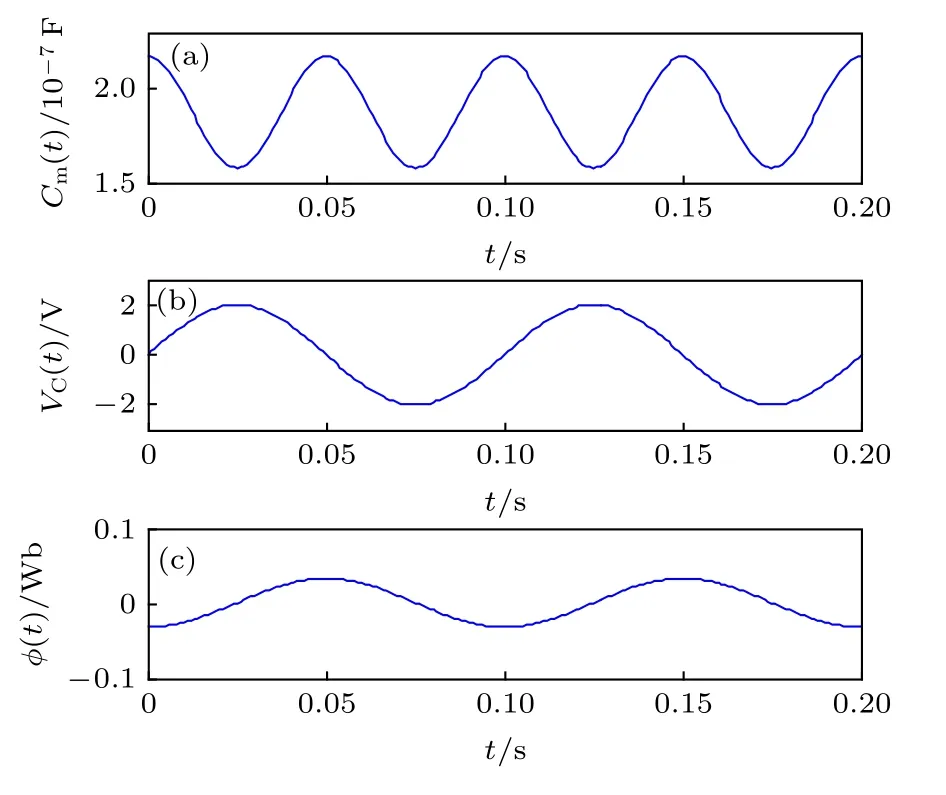
圖2 正弦交流電激勵下憶容器 Cm 、 vC和φ 的時域波形(a) Cm ;(b) vC ;(c)φFig.2.Time domain waveforms of Cm,vC and flux under periodic excitation signal: (a) Cm ;(b) v C ;(c) φ.

從磁通量 φ (t) 的 時域波形來看,在t∈ [0.025,0.05]s區間內,vC(t) 與 橫坐標圍成的面積即 φ(t)為正,且隨時間 t的增大而增大,故 Cm(t) 在該區間內呈增大趨勢.當 t=0.05s 時,φ (t) 達到最大,此時 Cm(t) 也 達到最大值.在 t ∈[0.05,0.075]s 區間內,vC(t) 與橫坐標圍成的面積為負,由于正負面積抵消,φ (t) 將 隨 t的增大而減小.當 t=0.075s 時,φ(t)=0,此時 Cm(t) 為最小值.

3 憶容器的非易失性

文獻[1]中定義了憶容器的本構關系,其中憶容值C或憶容值的倒數 C-1分別是狀態變量x和控制變量 vC(或q)的函數,且狀態變量與控制變量之間滿足積分關系,該關系體現了憶容器的記憶特性.觀察憶容器的狀態變量從非穩態到穩態的演變過程,判斷憶容器平衡點的穩定性,研究憶容器狀態保持或切換的規律和方法,利用憶容器穩定的憶容值,來表示二進制狀態或多值狀態,并應用于非易失性存儲器或數字邏輯運算等領域,是未來憶容器研究的重要方向.

Chua[16]提出了非易失性憶阻器理論.該理論表明: 一個具有標量狀態變量x的憶阻器是非易失性的,如果它的 Power-Off Plot (POP 斷電圖) 與x軸的交點有兩個或兩個以上是負斜率的.其中POP斷電圖是指: 憶阻器的狀態方程在外加激勵 v 或 i等于零,即 d x/dt=g(x,v)|v=0或 dx/dt=f(x,i)|i=0時,d x/dt 相對于x的動態路徑圖.

本文對該理論進行擴展,得出憶容器的非易失性理論: 若憶容器的POP斷電圖與狀態變量x (標量)所在軸的交點有2個或2個以上的點是穩定的平衡點,那么該憶容器是非易失性的.

由圖3可知,設置外加激勵 vS=0,則 (3)式中 φ =0,繪制憶容器的POP斷電圖如圖3中的藍色曲線所示.該曲線與坐標軸 φ 軸完全重合,故曲線上任意一點Q點均為憶容器的平衡點.由于所有平衡點處磁通量的變化率均為零,故憶容器可以穩定在任一平衡點上,即POP斷電圖與 φ 軸的交點有無窮多個穩定的平衡點.

假設憶容器穩定在如圖3所示的平衡點Q1(—0.6,0)處,在憶容器兩端外加幅度為 1 V 的直流電壓,其動態路徑如圖3中紅色曲線所示.此時憶容器的工作點從藍色曲線的Q1點跳變到紅色曲線 Q2(—0.6,1)點,并沿 φ 增大的方向運動.若經過 Δ t1時間后,工作點運動到 Q3(0.4,1)點,且同時撤銷激勵,即 vS=0,工作點將由Q3點跳變到藍色曲線的 Q4(0.4,0)點,并穩定在 Q4點的 φ 值上.若在憶容器的兩端外加幅度為—0.5 V的直流電壓,其動態路徑如圖3中綠色曲線所示.此時憶容器的工作點從藍色曲線的Q4點跳變到綠色曲線的 Q5(0.4,—0.5)點,并沿 φ 減小的方向運動.若經過 Δ t2時間后,工作點運動到 Q6(—0.2,—0.5)點,且同時撤銷激勵,即 vS=0,工作點將由Q6點跳變到藍色曲線的 Q7(—0.2,0),并穩定在 Q7點的 φ 值上.由以上分析可知,外加脈沖信號,可以使憶容器在多個穩定的平衡點之間進行轉換,或保持斷電前的狀態.脈沖信號幅度的正負決定了工作點運動的方向(即 φ 增大或減小的方向),脈沖信號寬度反映了脈沖作用的時間長短(決定了 | Δ φ| 值的大小).

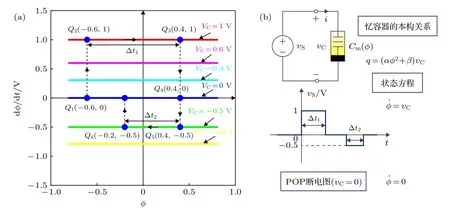
圖3 憶容器的動態路徑圖 (d φ/dt-φ ) (a)動態路徑圖;(b)憶容器電路和 Vs 波形Fig.3.Dynamic path map of memcapacitor (d φ/dt-φ ): (a)Dynamic path map ;(b) Memcapacitor circuit and Vs waveform.

4 憶容器仿真器設計

基于(3)式的憶容器數學模型,在文獻[14,19,20]的基礎上,利用電流反饋型運放、乘法器等器件構建了一個二次曲線模型的壓控型憶容器仿真器,如圖4所示.

圖4中U1、U5、U3和U4為電流反饋型運放AD844,U2 和 U6 為乘法器 AD633,U7 是電壓型運放 uA741.由 AD844 的數據手冊可知: x端和y端分別是反相和同相輸入端,且滿足 vx=vy.P和z均為輸出端,滿足 vz=vp.由于z端驅動負載的能力較弱,通常由P端外接負載.x端和z端流入 (或流出)的電流大小相等,滿足 ix=iz,y 端電流 iy=0.根據AD844芯片的端口特性可推得:vAB=i1R1,故

其中 U5、 R1和C1構成了積分電路,故

由 AD633芯片的數據手冊可知:vU3=(vx1-vx2)(vy1-vy2)/10+vz,且外圍電路設計滿足 vz=vU3R9/(R8+R9) 關系,設置 U6芯片vx2=vy1=0,R8=10kΩ,R9=22kΩ可實現關系,將 (6)式代入關系式中,可得

圖4 壓控型憶容器仿真器Fig.4.A voltage-controlled memcapacitor emulator.

由比例運放U7的性質可知:

將(7)式代入(8)式可得

設置 R6=10kΩ,R7=90kΩ,由 U2、 R6和R7組成的乘法器電路滿足關系式 vw=vU1·vU4,將(9)式代入關系式中,可得

因電容 C2的電壓 vw和 電流 iCM為關聯參考方向,故

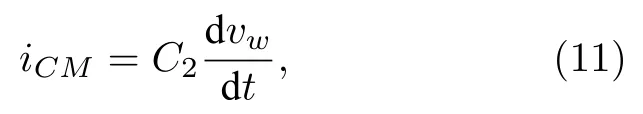
將(11)式等號兩邊積分可得:

將(10)式和(12)式代入到憶容器的本構關系中,可得

將(13)式化簡為

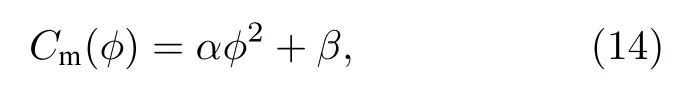
其中.

設置憶容器仿真器的電路參數為: R1=95kΩ 、R2=30kΩ 、 R3=30kΩ、R4=60kΩ 、 R5=30kΩ 、C1=C2=200nF 和VS=-15V.為了提高積分效果,減小失調和相移的影響,在電路仿真和實驗的過程中,在C1兩端并聯了820 kΩ的電阻.由(12) 式可知,電壓 vw和憶容器的電荷 qCM成正比,故 vw-vAB曲 線和憶容器的 q-v 特性曲線變化規律是一致的.在圖4所示的憶容器仿真器AB兩端外加振幅為 2 V,頻率分別為 3 Hz,5 Hz 和 10 Hz 的正弦交流電.通過電路仿真和硬件實驗電路的測試,分別獲得如圖5(a)和(b)所示的憶容器仿真器的 q-v 特性曲線.

由圖5(a)和(b)可知,仿真電路和硬件實驗電路的測試結果相同,且該曲線隨頻率增大而收縮的特性也完全一致.

圖5 憶容器仿真器的 q-v 曲 線(橫坐標和縱坐標分別對應于 v AB和vw ) (a)仿真電路的測試結果圖,縱坐標顯示范圍[—10,10]V,橫坐標顯示范圍 [—5,5]V;(b) 硬件實驗電路的測試結果,橫坐標和縱坐標顯示分別為 1 V/格和 2 V/格Fig.5.q-v pinched hysteresis loops of the memcapacitor simulator: the abscissa and ordinate correspond to v AB and v w,respectively: (a) Results of circuit simulation.The display range of ordinates is [—10,10]V,and the display range of abscissa is [—5,5]V;(b) result of hardware experiment circuit;the abscissa and ordinates are shown as 1 V/lattice and 2 V/lattice,respectively.

5 憶容器多諧振蕩器的設計與仿真

圖4所示的憶容器仿真器可以浮地也可以接地使用,本文將其應用在多諧振蕩器中,電路設計如圖6所示.U是型號為uA741的集成運放,其反相輸入端和輸出端之間接電阻R10,反相輸入端和地之間接如圖4所示的憶容仿真器.集成運放的同相輸入端和輸出端之間通過電阻 R12相連,同相輸入端和地之間接電阻 R11.集成運放由 ± 15 V 電源供電,ZD1和ZD2是型號為 1N4728 的穩壓管.設置振蕩電路中各參數的值分別為: R11=10kΩ 、R12=25kΩ 、 R10=300kΩ 和R13=125 Ω.

由基爾霍夫電壓定律可得:

由憶容器的本構關系及集成運放的“虛斷”可知,憶容器電壓 vC可表示為

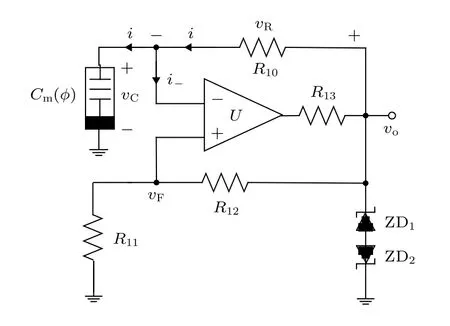
圖6 基于憶容器的多諧振蕩器Fig.6.Multivibrator based on memcapacitor.

其中,qC是憶容器的電荷,i是流過憶容器的電流.由(16)式整理可得

將(17)式代入(15)式可得

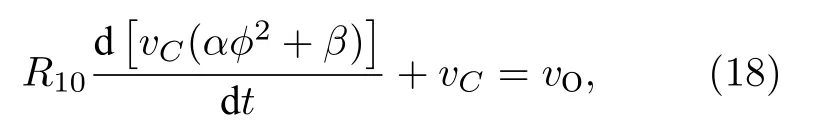
(18)式經化簡可推得

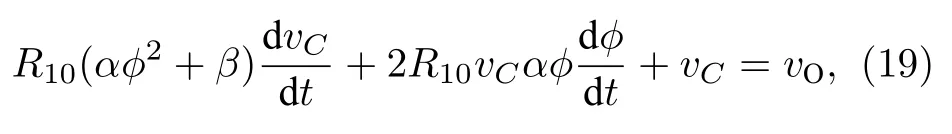
令 y1=φ,y2=vC,將 (19)式化簡為兩個聯立的一階微分方程,分別為

由于集成運放U滿足“虛斷”,故 R10Cm回路可視為串聯結構.由于(20)式的非線性程度較高,通過假設 vO無 法獲得 vC的解析解,只能通過數值解模擬外加方波信號 vO時 R10Cm回路中各變量的時域波形.假設 vO是幅值為 2 V,頻率為 5 Hz,占空比為0.5的方波信號,觀察憶容器的磁通 φ、憶容器電壓 vC和 電阻 R10電壓vR的時域波形,如圖7所示.

當 vO為高電平時,vO通過R10Cm回路對 Cm進行正向充電,此時 vC按非線性規律增大,vR將減小,直到 vO跳變為低電平.在 vO跳 變的同時,vR也將同時發生跳變,由于跳變瞬間憶容器電壓 vC的值不能躍變,故vR的反向峰值電壓的絕對值將高于 vO低電平的絕對值.之后,vO對 Cm進行反向充電,直到 vO再 次跳變為高電平.vO跳 變的同時,vR也將同時發生跳變,跳變瞬間由于憶容器電壓vC的值不能躍變,故 vR的正向峰值電壓的絕對值將高于 vO高電平的絕對值.圖5中憶容器磁通 φ 的波形是一個近似的拋物波,由 vC積分得到的.

圖7 R10Cm 回 路中憶容器的磁通、電壓和v R 的 時域波形 (a) φ ;(b) vC;(c) vO;(d) vR Fig.7.In R10Cm circuit,the time-domain waveforms of flux and voltage of the memcapacitor and voltage vR: (a) φ ;(b) vC;(c) vO;(d) vR.

對圖6中的憶容器多諧振蕩器進行電路仿真,得到如圖8所示的振蕩波形.其中 vO為振蕩器的輸出波形、 vC為 憶容器的端電壓波形、 vw為憶容器仿真器中U2芯片的輸出電壓波形(它反映了憶容器電荷q的變化規律),vU3為憶容器仿真器中U6芯片的輸出電壓波形(它反映了磁通-φ2的變化規律).設置電路參數R12/R11=2.5、R10=300kΩ和C2=200nF,在該電路參數下,測得憶容器多諧振蕩器的性能參數分別為:門限電壓|vT|=1.285V、振蕩周期T=0.182s、振蕩頻率f=5.454Hz和占空比D=0.516.

由于憶容器的憶容值Cm(φ)是非線性變化的,故其充放電過程比線性電容復雜得多.從圖8的仿真結果來看,憶容器多諧振蕩器有兩個輸出狀態vOH和vOL,其值取決于雙向穩壓管的穩壓值.若振蕩器上電瞬間vO=vOH,此時vOH通過R10Cm回路對Cm進行充電.當vC≥vF=vTH時,輸出電壓vO由vOH跳變為vOL,vTH是令輸出發生跳變所需的門限電壓,且vTH=R11vOH/(R11+R12).當vO跳變為vOL時,令輸出再次發生跳變所需的門限電壓變為vTL,且vTL=R11vOL/(R11+R12).此時vOL通過R10Cm回路對Cm進行反向充電,vC按照非線性規律衰減.當vC≤vF=vTL時,輸出電壓vO再次跳變為 vOH.

6 憶容器多諧振蕩器的硬件電路測試及性能分析

將本文設計的憶容器仿真器連接到如圖6所示的振蕩電路中,為了便于起振,在憶容器兩端并接一個8 nF的電容.考慮到限流電阻的功耗以及穩壓管的工作電流范圍,將R13設計為兩個250 Ω的并聯電阻,硬件電路測得振蕩波形如圖9所示.測得振蕩周期T=0.182s,振蕩頻率f=5.494Hz,占空比D=0.516.可見,實驗結果和仿真結果一致.

分別調整R12/R11、R10和C2的參數值,觀察振蕩周期T、振蕩頻率f以及占空比D隨參數變化的規律.在實驗的過程中,將其中的兩組參數固定,改變第3組參數,通過測試振蕩器的性能參數T、f和D,繪制性能參數隨電路參數變化的曲線,如圖10、圖11和圖12所示.

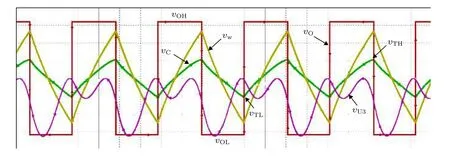
圖8 憶容器多諧振蕩器仿真電路波形(vO、vw和vC縱坐標的顯示范圍均為[-5.0,5.0]V,vU3縱坐標的顯示范圍是[-2.0,2.0]V)Fig.8.Simulation waveforms of memcapacitor multivibrator: The display range of vertical coordinates vO 、 vw and vC are all[-5.0,5.0]V,but the display range of vertical coordinates of vU3 is [ - 2.0,2.0]V.

圖9 硬件電路實測振蕩波形 (vo 、 vC和vw 幅 值均為 2 V/格,vU3 為 500 mV/格,時間軸均為 100 ms/格)Fig.9.Measurement of oscillating waveforms in hardware circuit: (The vertical axes of vo,vC and vw are both 2 V/lattice,the vertical axes of vU3 is 500 mV/lattice,The horizontal axes of all voltages are 100 ms/lattice).

設置電路參數R10=300kΩ 和C2=200nF,調整電路參數R12/R11的取值范圍,使其在[2.427,8.333]區間內變化,得到如圖10所示的實驗曲線.由于增大R12/R11會使門限電壓|vT|減小,故憶容器充放電到門限電壓所需的時間減小,導致振蕩周期T和振蕩頻率f,分別隨電路參數的增大單調遞減和單調遞增,其測量結果的范圍分別是T∈[64.67,181.6]ms和f∈[4.028,15.46]Hz.當振蕩頻率f隨參數的變化增大時,憶容器的非線性特性將退化,使充放電回路的時間常數相近,占空比D在理論上將趨于0.5(仿真結果),但是實際測量的過程中,由于R12/R11的取值范圍受限于[2.427,8.333],故實測的占空比范圍為[0.550,0.520].

當電路參數設置為R12/R11=5 和R12/R11=2.427時,分別測得如圖13(a)和圖13(b)所示的硬件電路實驗振蕩波形.其中振蕩器的輸出波形 vO、憶容器的端電壓波形 vC和反映憶容器電荷q變化規律的電壓波形 vw是同頻率的,測得兩種電路參數下振蕩頻率的大小分別為9.899 Hz (圖13(a))和4.028 Hz(圖13(b)).對圖6所示電路分析可知,R12/R11↓→|vT|↑→ T ↑→ f ↓,這與圖11所示的實驗結果完全吻合.由圖13(a)和圖13(b)的振蕩波形可知,電路的振蕩頻率f越小,憶容器的非線性程度越高,vw和vC瞬時值的差異越大,所反映的 q-v 滯 回特性越明顯.由 (7) 式可知,vU3與 vAB積分的平方成正比,故電路的振蕩頻率f越小,經積分平方之后的電壓幅值越大.從 vU3的振蕩波形來看,當振蕩頻率低至某一數值時,乘法器的輸出端將產生輸出飽和現象,導致憶容器仿真器中各級電路的電壓運算過程出錯.

圖10 R12/R11 作為參變量時,振蕩器性能參數隨電路參數變化的曲線 (a) T;(b) f;(c) DFig.10.Curve of Oscillator Performance Parameters with Circuit parameter changes (R12/R11 as a parameter variable): (a) T;(b) f;(c) D.

圖11 R10 作為參變量時,振蕩器性能參數隨電路參數變化的曲線 (a) T;(b) f;(c) DFig.11.Curve of oscillator performance parameters with circuit parameter changes (R10 as a parameter variable):(a) T;(b) f;(c) D.

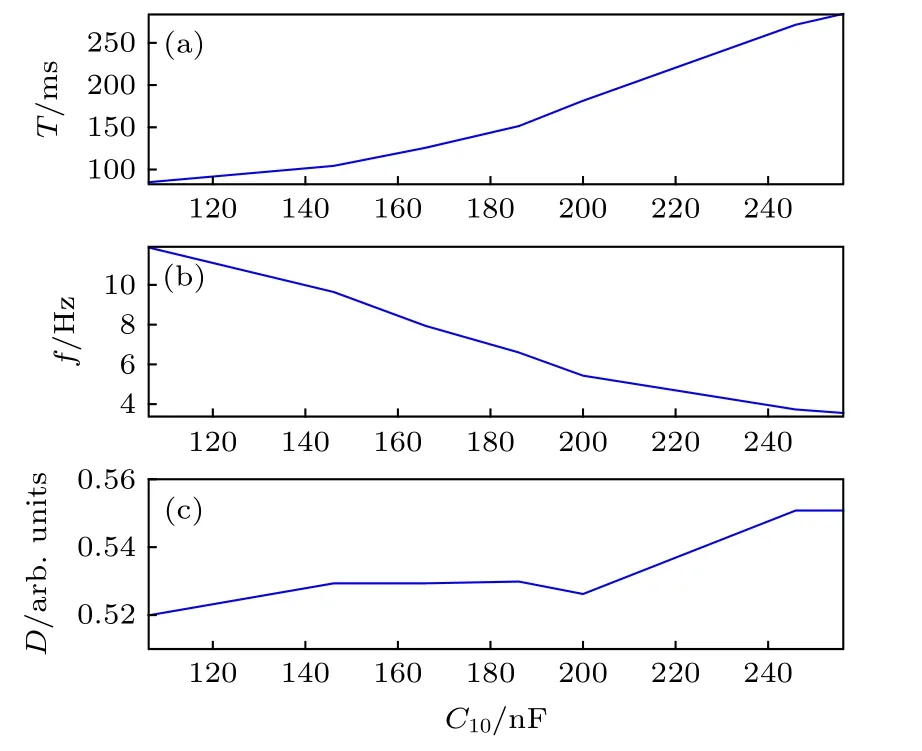
圖12 C2 作為參變量時,振蕩器性能參數隨電路參數變化的曲線 (a) T;(b) f;(c) DFig.12.Curve of Oscillator Performance Parameters with Circuit parameter changes (C2 as a parameter variable):(a) T;(b) f;(c) D.

設置電路參數C2=200nF 和R12/R11=2.5,調整參數 R10的 取值范圍,使其在 [ 1 60,324]kΩ 區間內變化,得到如圖11所示的曲線.由于 R10的值越大,R10Cm回路充放電的時間常數越大,憶容器充放電到門限電壓 | vT| 所需的時間越長,導致振蕩周期T和振蕩頻率f分別隨參數的增大單調遞增和單調遞減,其測量結果的范圍分別是 T ∈ [94.5,263.69]ms和f ∈[3.7929,10.606]Hz.由 圖11可知,因振蕩頻率f減小導致憶容器的非線性特性增強,使振蕩電路充放電回路的時間常數平均值差異變大,占空比D變大.

圖13 憶容器振蕩器硬件電路實驗振蕩波形 (圖 (a)和 (b)中 vO 、 vC和vw 的 縱軸均為 2 V/格) (a) R12/R11=5,其中 vU3 縱軸為 100 mV/格,時間軸為 50 ms/格;(b) R12/R11=2.427,其中 vU3 縱軸為 5 V/格,時間軸為 100 ms/格Fig.13.Experimental oscillation waveforms of memcapacitor multivibrator: (a) R12/R11=5 ;(b) R12/R11=2.427.The vertical axes of vO 、 vC and vw in Fig(a) and Fig (b) are both 2 V/lattice.The vertical and horizontal axes of vU3 in Fig(a) are 100 mV/lattice and 50 ms/lattice,respectively.The vertical and horizontal axes of vU3 in Fig(b) are 5 V/lattice and 100 ms/lattice,respectively.

當電路參數設置為 R10=202kΩ 和R10=324kΩ時,分別測得如圖14(a)和圖14(b)所示的硬件電路實驗振蕩波形.測得兩種電路參數下 vO、 vC和vw振蕩頻率的大小分別為 8.348 Hz (圖14(a))和3.793 Hz ((圖14(b)).對圖6 所示電路分析可知,R10↑→τ↑→T ↑→ f↓,這與圖14所示的實驗結果完全吻合.與圖13分析結果類似,電路的振蕩頻率 f越小,憶容器的非線性程度越高,vw和vC瞬時值的差異越大,所反映的q-v滯回特性越明顯.在電路參數 R10調節的過程中,要注意振蕩頻率較低時,避免乘法器輸出端出現飽和現象.

設置電路參數 R10=300kΩ和R12/R11=2.5,調整參數 C2的取值范圍,使其在[106,256]nF 區間內變化,得到如圖12所示的曲線.由(13)式憶容值的表達式可知,C2的值越大,在周期信號激勵下的憶容瞬時值 Cm(φAB) 越大,充放電回路時間常數的瞬時值越大,憶容器充放電到門限電壓 | vT| 所需要的時間越長,導致振蕩周期T和振蕩頻率f分別隨參數的增大單調遞增和單調遞減,其測量結果的范圍分別是T ∈[84.49,285.99]ms 和f ∈ [3.498,11.822]Hz.由圖12可知,在測量區間內占空比D隨 C2的 增大而單調遞增,說明 C2的增大會導致憶容器充放電回路的時間常數的平均值差異變大.

當電路參數設置為 C2=146nF 和C2=256nF時,分別測得如圖15(a)和(b)所示的硬件電路實驗振蕩波形.測得兩種電路參數下 vO、 vC和vw的振蕩頻率的大小分別為 9.649 Hz (圖15(a))和3.498 Hz (圖15(b)).對圖6 所示電路分析可知,C2↑→Cm↑→ τ↑→T ↑→ f↓,這與圖13所示的實驗結果完全吻合.電路的振蕩頻率f與憶容器的非線性程度之間的關系,以及電路中的輸出飽和問題與圖13和圖14中的分析結果類似,此處不再贅述.

從三組參數對振蕩頻率調節的范圍來看,參數R12/R11對憶容器多諧振蕩器振蕩頻率調節的范圍最寬.同時也發現,利用憶容器的非線性特性只能小范圍地改變振蕩器的占空比大小.

圖14 憶容振蕩器硬件電路實驗振蕩波形(圖中vO 、 v C和v w縱軸均為2 V/格,圖 (a)中 v U3 縱軸為 500 mV/格,時間 軸為50 ms/格,圖 (b)中 vU3 縱 軸為 5 V/格,時間軸為 100 ms/格) (a) R10=202kΩ ;(b)R10=324kΩFig.14.Experimental oscillation waveforms of memcapacitor multivibrator: (a) R10=202kΩ ;(b) R10=324kΩ.The vertical axis of vO 、 v C and v w in Fig.(a) and Fig.(b) are both 2 V/lattice.The vertical and horizontal axes of v U3 in Fig.(a) are 500 mV/lattice and 50 ms/lattice,respectively.The vertical and horizontal axes of v U3 in Fig.(b) are 5 V/lattice and 100 ms/lattice,respectively.

圖16(a)和 圖16(b)分別為 R10=202kΩ 和R10=324kΩ時在硬件電路實驗中所測得的憶容器q-v曲線,它是一個緊致滯回曲線.曲線上各點的斜率體現了憶容器仿真器容值 Cm的變化規律.由圖16可知,在振蕩頻率較低時,圖16(b)中的滯回曲線是不關于原點對稱的,且振蕩頻率越低,對稱性越差.當振蕩頻率增大后,圖16(a)中滯回曲線的磁滯旁瓣面積相比圖16(b)有所減小,但關于原點的對稱性比圖16(b)更好.

圖15 憶容振蕩器硬件電路實驗振蕩波形 (圖中 vO 、 v C和v w縱軸均為 2 V/格,圖 (a)中 v U3 縱軸 為 500 mV/格,時間軸為50 ms/格,圖 (b)中 v U3 縱軸為 2 V/格,時間軸為 100 ms/格) (a) C2=146 nF;(b) C2=256 nFFig.15.Experimental oscillation waveforms of memcapacitor multivibrator: (a) C2=146 nF;(b) C2=256 nF.The vertical axes of vO 、 v C and v w in Fig.(a) and Fig.(b) are both 2 V/lattice.The vertical and horizontal axes of v U3 in Fig.(a) are 500 mV/lattice and 50 ms/lattice,respectively.The vertical and horizontal axes of v U3 in Fig.(b) are 2 V/lattice and 100 ms/lattice,respectively.

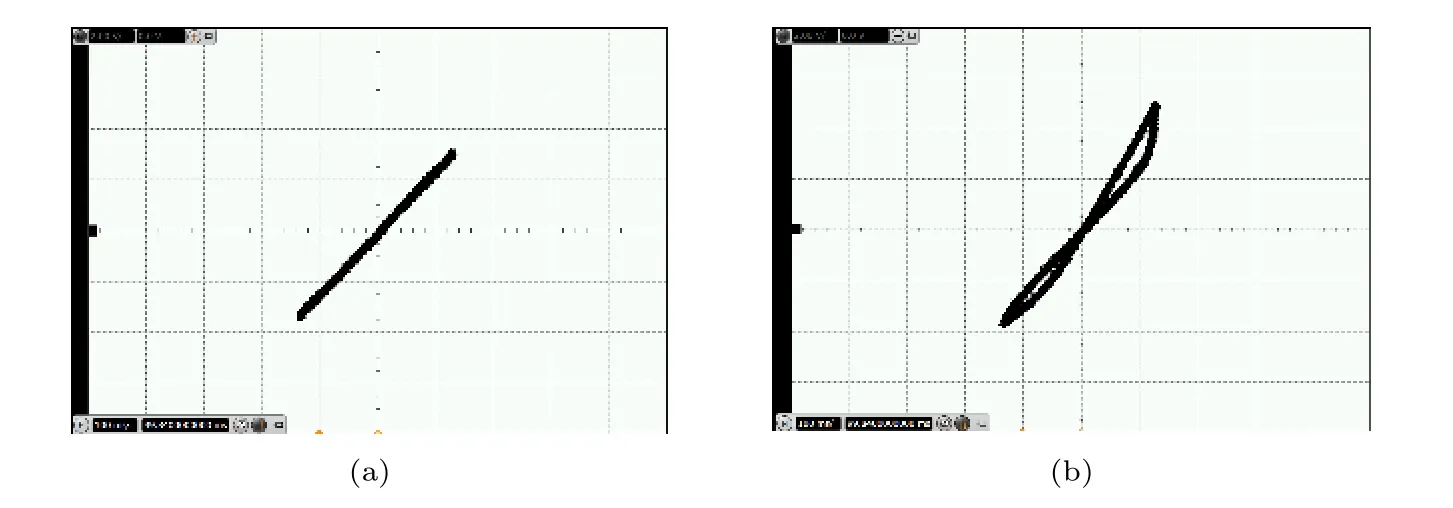
圖16 R10為不同值時振蕩電路中憶容器的滯回曲線(橫坐標和縱坐標分別對應于vAB和vw ) (a) R10=202kΩ ;(b)R10=324kΩFig.16.The pinched hysteresis loops of memcapacitor with different values of R10 in oscillating circuit: (a) R10=202kΩ ;(b)R10=324kΩ.The horizontal and vertical axes correspond to vAB and vw,respectively.

7 結 論

本文提出了一種壓控型憶容器的二次曲線模型,并利用模擬器件構建了憶容器仿真器.該仿真器不需要通過憶阻器或憶感器轉換得到,可以浮地也可以接地使用,并能動態模擬憶容器的伏庫特性曲線,便于研究和測試憶容器在不同頻率周期信號激勵下的滯回曲線.分析了憶容值的取值范圍隨激勵參數變化的規律,著重分析了憶容器的非易失性和平衡點的穩定性,總結了憶容器在幾種不同記憶狀態間的切換規律.將憶容器應用到多諧振蕩器中,通過理論分析推導了該電路的狀態方程,對振蕩器的工作原理進行了解釋,并對電路的振蕩波形進行了仿真和測試.該憶容器多諧振蕩器結構簡單,起振較快且波形的穩定性較好.從實驗結果來看,對電路參數R12/R11、R10或C2進行調整,均可以改變多諧振蕩器的振蕩周期T、振蕩頻率f和占空比D.振蕩電路性能參數的改變主要是由于充放電回路時間常數的平均值的大小及差值發生的變化所致.由于各級運放和乘法器存在輸出飽和現象,仿真器電路的參數調節范圍受限,依靠憶容器的非線性特性大幅改變占空比是很難做到的.如需實現占空比的大幅調節,可以將負反饋網絡中的電阻 R10,用一個并聯網絡來替換.并聯網絡中兩條并聯支路均由二極管和電阻串聯而成,且兩個二極管為反向接入方式.當兩條支路中的電阻阻值不同時,可以大幅改變充放電回路的時間常數,從而引起占空比的大幅改變.