類巖石材料的彈性損傷-滲流耦合模型研究

王 慶，姚 俊，譚文祿

(中電建生態環境集團有限公司，廣東 深圳 518102)

在邊坡[1-2]、壩基[3]、隧洞[4]等巖石工程中，經常會遇到地下水與巖石(體)之間的耦合問題，其作用機理是：一方面，當巖石(體)變形時會引起孔隙率、節理厚度等變化，從而引起滲流場的變化；另一方面滲流場變化會引起孔隙水壓力和有效應力的變化，從而引起巖石(體)應力應變場的變化。對應力滲流耦合最早的研究是Biot的三維固結理論[5]，但該理論中滲透系數在變形過程中為常數。有關學者的研究表明[6-9]，滲透系數在巖石的變形破壞過程中，會發生較大的變化，可能會影響工程的安全性，法國Malpasset拱壩失事正是沒有考慮到滲透系數變化而導致的[10]，因此有必要研究巖石變形過程中滲透系數的變化規律。

目前應力滲流耦合的研究方法主要分為宏觀唯象和細觀2類方法。宏觀唯象方法又可以分為直接法和間接法。直接法是指通過室內室外實驗對實驗數據進行擬合得到經驗公式的方法[11-12]，這些公式只能反映巖石變形過程中滲透系數的變化的某一階段，不能體現應力峰值后的變化規律。為了克服經驗公式的這一缺點，學者們開始研究全應力-應變過程中的滲透系數變化規律[13-16]，但由于公式的參數太多，形式受巖石性質、實驗條件等影響太大，而且不能解釋滲透系數變化的物理力學機理，因此不利于在工程中應用。間接法則是通過引入中間變量，間接建立應力(應變)與滲透系數之間的關系，最常用的中間變量是孔隙率[17]。間接法雖然能減少模型參數數量，但巖石應力應變全過程不同階段的滲透系數變化的機理不同，如峰前滲透系數急劇增大的主要原因是微裂紋擴展，而不是孔隙率變化，因此用一個中間變量很難描述全過程的滲透系數變化規律。細觀方法是通過描述巖石在變形過程中細觀結構(孔隙、微裂紋等)的變化，從而引起滲透系數變化的方法[18-20]。細觀方法可以解釋巖石變形過程中的滲透系數變化機理，但計算過程中需要記錄每一個微裂紋的傾向、傾角、開度等參數，因此需要借助計算機程序實現。

為了提出既能解釋滲透系數的變化機理，又方便應用的模型，許多學者開始從等效連續介質的角度將巖石細觀結構的變化等效為損傷演化[21-23]。將損傷作為連接應力(應變)和滲透系數之間的橋梁，建立巖石、混凝土、水泥砂漿等類巖石脆性材料的彈性損傷-滲流耦合模型，這個耦合過程中有2個重要的準則，一個是損傷的演化準則，另一個則是損傷過程中的滲透系數變化準則，本文在傳統的彈性損傷模型和滲透性變化模型基礎上，提出改進的彈性損傷-滲流耦合模型。

1 改進的彈性損傷模型

傳統的巖石彈塑性損傷模型，雖然有可以考慮塑性和可以區分拉壓破壞的優點，但是該本構關系也有一些缺點。首先是輸入參數過多，彈塑性損傷本構關系中拉壓曲線是分開的，而且要輸入塑性強化的應力～應變曲線以及損傷因子隨著開裂應變的變化曲線，這些曲線的參數過多；另外一點是使用彈塑性損傷本構關系計算，結果很難收斂，而且收斂性也不能控制。鑒于這兩個缺點，這里在Mazars模型的基礎上，改進其收斂性和網格依賴性，提出一種改進的彈性損傷模型。Mazars模型是一種描述混凝土損傷的本構關系，在該模型中，應力應變關系如下：

(1)

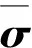
(2)

(3)

(4)

其中，ABS()是取絕對值函數，如果f為正，結果為f；如果為負，結果為0。

在Mazars模型中，等效應變作為內變量來判斷損傷的初始化和演化，但是這里是將有效應力分解為拉壓部分，按照這種思想，將拉壓有效應力的等效應力作為損傷初始化準則，形式如下：

(5)

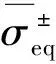
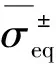
(6)

(7)

(8)

(9)

式中：

(10)

(11)

(12)

(13)

式(6)、(8)是受拉損傷的初始化準則，其形式和最大拉應力準則類似，式(7)、(9)是受壓損傷的初始化準則，由于受壓破壞中含有壓縮和剪切破壞的組合，其形式類似于Drucker-Prager屈服準則，K是Drucker-Prager屈服準則的錐角，R0是雙軸壓縮強度和單軸壓縮強度比，f±是拉伸和壓縮強度。

Mazars模型中的損傷演化準則形式如下：

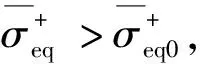
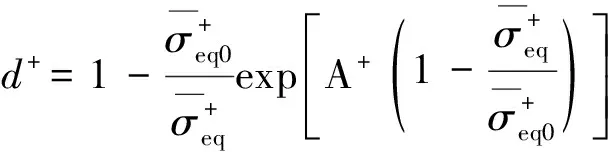
(14)

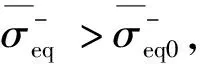
(15)

材料的軟化階段會導致邊值問題的不適定，式(14)、(15)中的損傷演化準則對網格的依賴性很大，為了減小網格依賴性，這里采用斷裂能的手段[25]來修正損傷演化準則。常數A+和B-可以寫成如下斷裂能的形式：

(16)

(17)

(18)

式中G±——拉壓斷裂能；lc——微裂紋的特征長度；Ve——單元體積；E0——初始彈性模量。

考慮拉損傷和壓損傷的總的損傷因子定義如下：

d=1-(1-d+)(1-d-)

(19)

以上的改進策略可以減小網格依賴性，但是材料軟化在隱式分析中，如ABAQUS Standard, 還存在收斂性問題，這里采用正則化準則來處理收斂性問題。正則化準則的主要目的是使軟化材料的切線模量在增量步足夠小的時候保持正定。根據式(1)中的應力-應變關系，可以得到Jacobian矩陣的形式如下:

(20)

為了提高收斂性，ABAQUS子程序UMAT中使用一種損傷因子的黏性正則化準則，此時，不直接使用式(14)、(15)來計算損傷因子，而是使用如下形式的正則化損傷因子：

(21)

(22)

(23)

(24)

從式(23)和式(24)中可以看出：

(25)

因此，使用正則化損傷因子計算得到的Jacobian矩陣形式如下：

(26)

需要注意黏性系數η的選擇，過小的黏性系數導致收斂所需要的增量步很小；過大的黏性系數可能會過度延遲剛度的弱化，導致軟化階段的應力-應變曲線偏離實際過多。

2 損傷過程中滲透系數的變化

巖石的壓縮過程中滲透性試驗中反應出滲透系數的變化通常具有幾個階段。根據Zhang[26]的試驗數據描繪的典型滲透系數變化的幾個階段見圖1。A是應力-應變曲線中損傷開始的點，對應于滲透系數開始快速增大的點，B點是應力-應變曲線中的峰值應力點，對應于滲透系數曲線的轉折點，B點之后滲透系數增長速度有所降低，然后達到滲透系數最大的點C，對應于應力-應變曲線的轉折點，C點之后應力下降速度減緩。OA階段滲透系數變化不大，但是有時候在開始的時候滲透系數有所減小，原因是在壓應力作用下孔隙變化和初始微裂紋的閉合。AC階段滲透系數的增大主要是因為微裂紋數目的增多以及微裂紋的張開，C點之后滲透系數的減小主要是因為試件破壞之后在圍壓的作用下宏觀裂紋閉合造成的。

圖1 脆性巖石的典型應力-應變曲線和滲透系數-應變曲線

目前描述脆性巖石壓縮過程中滲透系數的變化的經驗模型和理論模型只能描述滲透系數變化的某個階段，通常是增大的階段，并不能同時描述滲透系數變化的整個過程。假設巖石在壓縮過程中的滲透系數的變化主要由孔隙閉合引起的滲透系數減小和局部損傷引起的滲透系數增大這2個因素造成的。描述孔隙閉合引起的滲透系數減小現象的理論有Kozeny-Carman模型，形式如下：

(27)

式中Kp——孔隙閉合引起的滲透系數變化；c——一個與細觀結構有關的常數；n——孔隙度。

假設巖石顆粒不可壓縮，Vp是孔隙的體積；Vs是巖石顆粒的體積；e0是初始孔隙比；Δe是孔隙比的變化，則體積應變為：

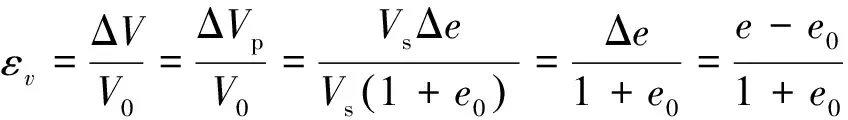
(28)

考慮到孔隙比和孔隙率的關系e=n/(1-n)，代入式(28)可以得到孔隙率和體積應變的關系：

(29)

式中n0——初始孔隙率。

將式(29)代入式(27)中，得到滲透系數隨著體積應變變化關系為：

(30)

(31)

在描述損傷引起的滲透系數增大方面，本文將從局部損傷的角度推導出滲透系數的變化，可以看出在精度要求不高的時候，理論公式和經驗公式的形式類似。在細觀結構中存在著初始裂紋和后來發展的微裂紋，細觀結構中的滲流主要受到這些微裂紋的影響，微裂紋中的滲流滿足平行板定理，其滲透系數為：

(32)

式中u——微裂紋的張開度；ξ——微裂紋的粗糙度。

雖然式(32)比較簡單，但是需要知道微裂紋的幾何產狀，而且本文的計算方法是基于連續介質的，所以按照微裂紋的思想，用損傷帶代替微裂紋來描述滲流通道的改變，見圖2。一個面積為S的截面受到單位水頭梯度的作用，材料沒有損傷部分的滲透系數為K0，材料的局部損傷帶的寬度為λlc，在具體計算過程中可以看作是單元的特征長度。等效的思想是讓損傷帶和微裂紋的流量相等，具體如下：

(33)

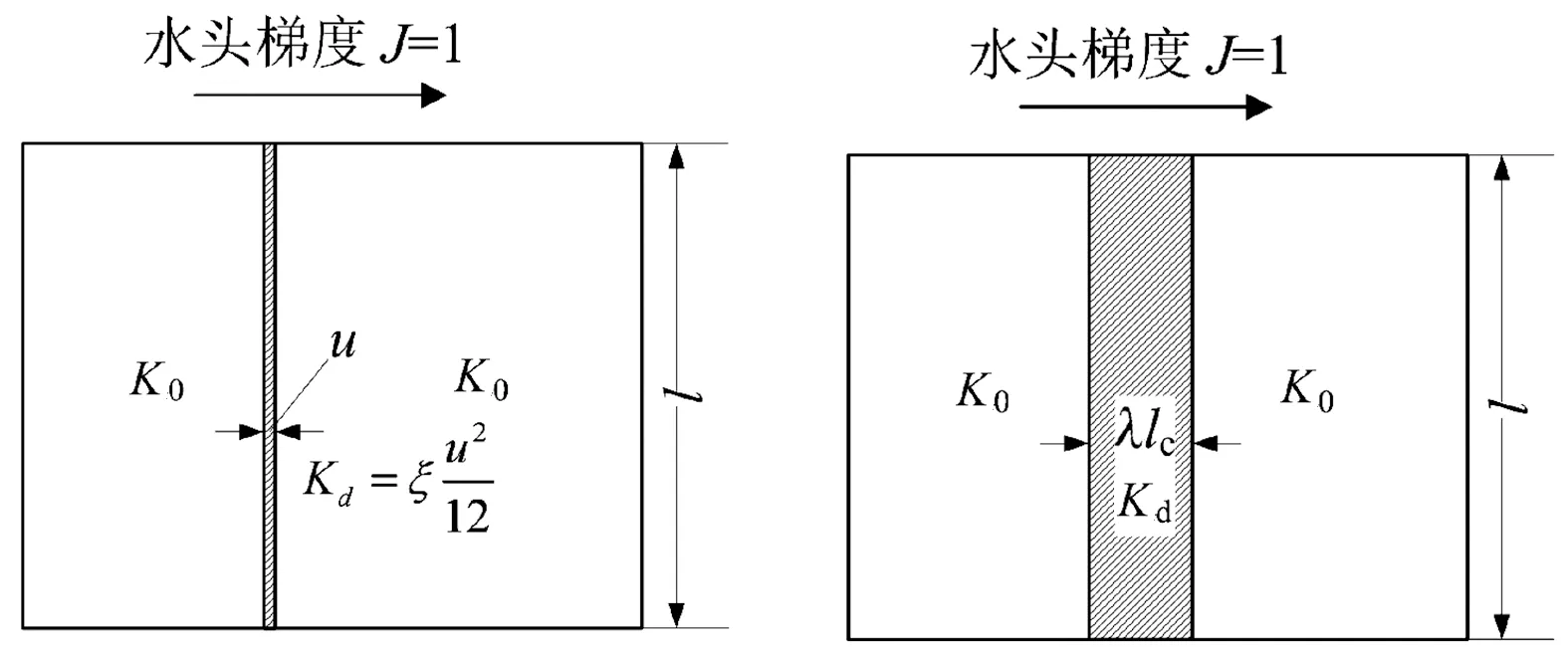
a) 微裂紋 b) 損傷帶

由式(33)可以得到損傷帶的滲透系數為：

(34)

ξ代表了微觀滲流通道的彎曲程度。最重要的是微裂紋開度u的計算，本文通過改進的彈性損傷模型來得到裂紋開度。在擴展有限元中，裂紋的張開是通過位移跳躍來表示的，而在漸進損傷理論中，裂紋的張開是通過損傷帶的法向累積位移表示的，所以這里只考慮拉損傷造成的滲透系數變化，在不考慮卸載造成的裂紋閉合的情況下，裂紋的張開可以表示為：

(35)

假設損傷帶內的應變是均勻的，式(35)的積分結果為:

(36)

要得到裂紋張開度和損傷的關系，需要求得式(14)的反函數的解，這里反函數沒有顯式解，需要通過迭代等數值方法得到，假設反函數的解已經得到，形式如下:

(37)

將式(37)代入到式(36)中得到微裂紋的開度：

(38)

將式(38)代入到式(34)中就可以得到損傷帶的滲透系數，但因為式(37)沒有顯式解，所以需要簡化。之前提到過理論推導的損傷帶滲透系數的公式在計算精度要求不高的時候，和指數型經驗公式有類似的形式，通過這一關系可以將損傷帶滲透系數簡化為指數型公式。將式(14)的指數項展開成泰勒級數，并取一次項，得到反函數的簡化解為：

(39)

至此，由孔隙閉合引起的滲透系數減小和局部損傷引起的滲透系數增大都考慮到了。所以，能同時考慮滲透系數變化不同階段的模型可以通過結合Kozeny-Carman公式和指數型公式得到，形式如下：

K=Kp(1+αdβ)

(40)

式中，α、β是與微裂紋幾何產狀有關的常數。將式(30)代入式(40)中得到損傷過程中滲透系數變化公式為：

(1+αdβ)

(41)

3 數值算例

3.1 模型邊界和參數

選取水泥砂漿材料作為研究對象，具體成分是砂子、水泥和水，其水灰比為0.4，砂子重量占40%，水泥漿和砂子的密度分別為2 000、2 650 kg/m3，在不考慮氣孔的情況下，細觀結構中基質和砂子的體積比分別為67%、33%。砂子采用的粒徑小于0.5 mm的河砂，假設砂子的粒徑滿足在區間[0.3,0.5]之間的均勻分布。有限元模型大小為4×4×4(mm3)，位移邊界條件為在模型下邊界施加固定約束；由于需要研究峰值后的應力應變規律，故采用位移邊界來代替荷載邊界，在模型上邊界勻速施加0.04 mm的位移，對應的最大豎向應變為0.01；滲流邊界為在模型上邊界施加1 kPa恒定不變的孔隙水壓力，下邊界為自由透水邊界，其他邊界為不透水邊界，見圖3。基質和顆粒的力學和滲流參數見表1、2。

圖3 水泥砂漿的細觀模型

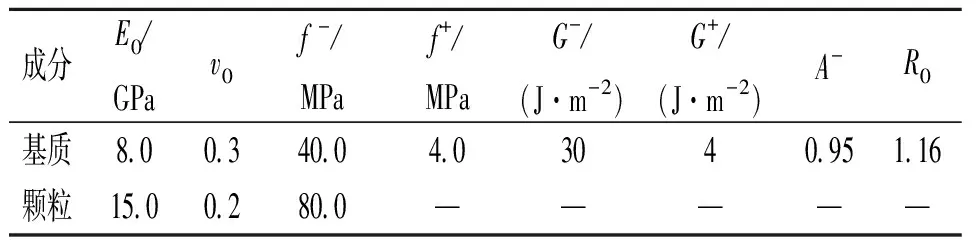
表1 細觀成分的力學參數

表2 細觀成分的滲流參數

3.2 結果分析

由于水泥砂漿材料的細觀模型中含有基質(水泥漿)和顆粒(砂子)2種組分，分析水泥砂漿的應力應變和滲流特性必須綜合基質和顆粒的應力場和滲流場，因此結果分析中將采用等效宏觀應力和等效宏觀滲透系數來表示水泥砂漿的特性。等效宏觀應力是細觀模型應力場的體積平均值：

(42)

等效宏觀滲透系數的處理方式與等效宏觀應力有所不同，首先根據細觀模型的流速場計算等效宏觀流速：

(43)

然后根據達西定律求解等效宏觀滲透系數：

(44)

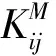
單軸壓縮應力-應變曲線和滲透系數變化曲線見圖4。可以看出宏觀應力-應變曲線和室內實驗數據吻合得很好，室內實驗中的試件由于初始裂紋的存在，導致在彈性階段初有一個壓密階段，峰后階段改進的損傷模型軟化曲線比較平滑。由于滲透實驗數據的缺乏，所以這里不進行滲透系數曲線的對比，但可以看出滲透系數的變化曲線與Zhang[26]的試驗數據一致，可以分為3個階段，但應力峰值后的滲透系數減小階段比Zhang的試驗數據平緩，其原因可能是本文中的模型不考慮卸載后細觀裂紋的閉合效應。相應于應力應變曲線上A和B點的損傷和流速云，見圖5、6。在峰值應力點A，損傷在基質和顆粒接觸的附近區域開始發展。在殘余應力點B，損傷區域逐漸發展到充滿基質。由于顆粒不透水，所以滲流只發生在基質中，顆粒中沒有流速場。

a)應力-應變曲線

b)滲透系數-應變曲線

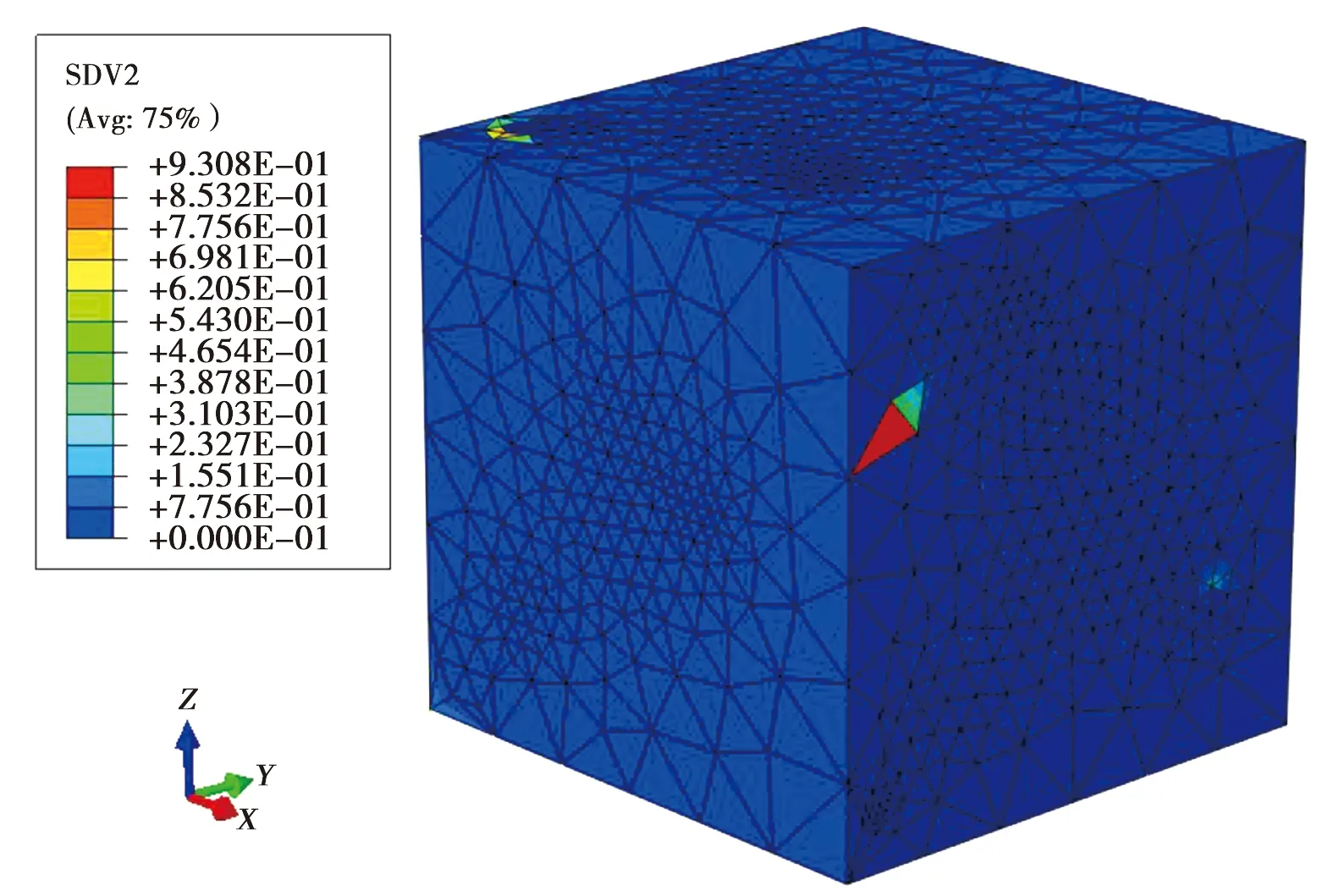
a)A點

b)B點

a)A點

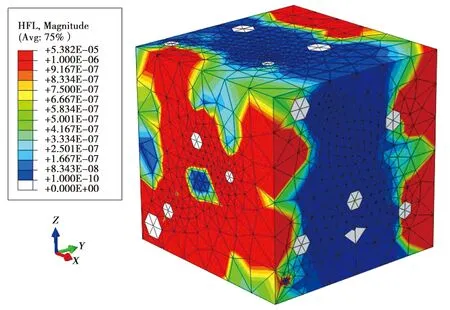
b)B點

4 結論

類巖石材料的應力-損傷-滲流耦合模型需要研究變形過程中的損傷演化和滲透系數隨損傷變化這兩個規律。本文提出一種改進的彈性損傷模型；同時將孔隙壓密階段和裂紋擴展階段的滲透系數變化過程統一起來，提出改進的全應力應變過程中滲透系數-損傷演化模型。最后通過在水泥砂漿材料的細觀模型上實施單軸壓縮數值實驗，得出以下結論。

a) 數值實驗的應力應變曲線和室內實驗結果吻合，表明改進的彈性損傷模型用來模擬類巖石脆性材料的有效性。

b) 數值結果可以明顯識別滲透系數在應力應變全過程中的不同階段，在應力達到峰值前由于孔隙不斷壓密，滲透系數不斷減小；在應力峰值附近，應變為0.004時，滲透系數突然增大，是因為此時開始出現損傷區域；在應力峰值附近，應變為0.007時，滲透系數達到最大值。

c) 由于缺少滲透系數的室內實驗數據，本文的滲透系數-損傷演化模型的參數還需進一步通過實驗確定，但滲透系數曲線趨勢基本能反映出Zhang[24]的試驗數據規律。