高壓高轉速螺旋槽干氣密封浮環變形研究*

丁雪興 王晶晶 張偉政 陸俊杰2 陳金琳

(1.蘭州理工大學石油化工學院 甘肅蘭州 730050;2.浙江大學寧波理工學院 浙江寧波 315010)

隨著制造業和工業化進程的不斷完善，軸端密封的旋轉機械不斷突破設計工況，逐步向極端工況發展，這對密封更是一項巨大的挑戰。在傳統的迷宮密封、刷式密封中，由于氣流的激振、密封件自身的磨損和轉子系統易發生干磨等因素，導致密封泄漏量增大、穩定性極差、壽命極短。因此研究人員提出了一種新型的柱面螺旋槽干氣密封，該密封具有泄漏少、磨損小、壽命長、結構緊湊等特點[1-4]。

對于柱面氣膜密封的研究，ZHANG等[5]在浮環密封上開設了槽形結構并分析了其穩定性和碰磨情況，結果表明開槽要比無槽好。MELNIK[6]研究了柱面密封的性能參數并提出一種具有更高的計算速度和精度的計算思想。KE等[7]研究了不同的密封條件對高速球軸承內流場的影響。XU等[8]提出了一種新型的預測液體環形密封動態特性的瞬態CFD方法，并同時計算了不同長度的液體環形密封件的動態特性。ASHTON[9]測量了高溫和軸表面速度為26 m/s時的混合刷式密封中的泄漏量和壓差，結果優于類似大小的傳統迷宮密封；而且隨著溫度的升高，迷宮密封的泄漏減少，因為其間隙由于部件的熱增長而改變。ZHANG等[10]提出了一種新的徑向環形密封，減小了流體泄漏損失和流體誘導力，且和傳統的迷宮密封相比，其泄漏方向由軸向改為徑向。丁雪興等[11]用PH線性化方法求得了氣體壓力的近似解析解，并用MATLAB軟件得到了氣膜壓力分布。陸俊杰[12]從理論計算和試驗研究兩個方面對單列螺旋槽、單列一字平行槽、雙列人字螺旋槽和雙列一字平行槽的氣膜的潤滑特性進行了研究。潘康毅等[13]運用差分法參考徑向軸承動潤滑理論探究了密封長度-油液黏度和密封間隙對浮環密封性能的影響。馬利軍等[14]研究發現，相比于整體石墨環，高溫鑲裝式浮環密封更有利于調整徑向間隙且過盈量對其間隙影響較小。

對于變形的研究，丁雪興等[15]采用有限元ANSYS軟件，對螺旋槽干氣密封補償環進行了力變形分析。趙芳等人[16]對干氣密封的靜環做了力變形分析研究。扈中平[17]在流固耦合的條件下對低溫干氣密封的動靜環分別進行了熱變形和力變形的研究。黃思等人[18]對IS100-65-200型單級離心泵的葉輪、螺母和軸等轉子系統進行了單向流固耦合分析。程香平等[19]研究了大菱形孔端面密封環的變形，并計算了不同結構及不同操作工況條件下密封環的摩擦扭矩、液膜剛度及泄漏率。湯赫男等[20]采用流固耦合方法分析了齒形角對往復式壓縮機迷宮密封內部流場及密封性能的影響。袁瑋瑋等[21]利用流固耦合方法對螺桿膨脹機轉子的內部流場和力變形進行了分析。

綜上所述：柱面密封的研究多數集中于數值求解的方法，針對端面的變形研究已經獲得了大量成果，但是考慮高壓下柱面浮環的變形卻很少見，因此高壓下浮環變形的研究對柱面氣膜密封的發展具有重大的意義。本文作者采用Solidworks建模軟件建立了流固耦合模型，然后針對柱面螺旋槽氣膜的特殊性，利用精度較高的ICEM結構化網格進行劃分；隨后采用仿真軟件Fluent對氣膜流場進行數值模擬計算；最后通過ANSYS Workbench的靜力學分析軟件Static Structure將流場求得的壓力耦合到浮環固體面上進行力變形求解，并進行浮環參數與工況之間的變化討論。

1 模型的建立

1.1 幾何模型

柱面螺旋槽干氣密封由浮動環、軸、軸套、密封支座、定位銷、壓緊彈簧等組成，其結構如圖1所示。軸與軸承相連，軸套過盈配合在轉軸上，與軸一起轉動。浮環安裝在密封支座腔體內部，與軸套形成微間隙。

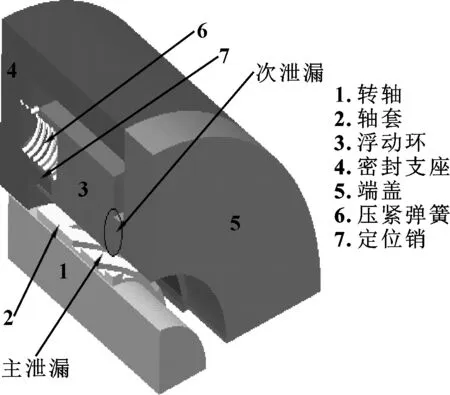
圖1 柱面螺旋槽干氣密封結構Fig 1 Structure of cylinder spiral groove dry gas seal

根據柱面密封的結構和工作原理可知浮環的受力情況，如圖2所示。浮環一端被定位銷固定，另一端受到彈簧力Fs，浮環內側受到氣膜反力F，浮環外側受到介質壓力p。

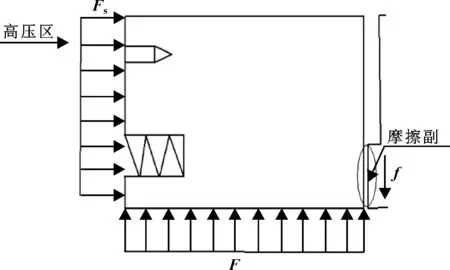
圖2 浮環受力圖Fig 2 Force diagram of floating ring

1.2 氣膜流域

利用建模軟件Solidworks分別對浮環和軸套進行實體模型的創建，然后進行偏心安裝，形成流固耦合計算模型，如圖3所示。模型參數如表1所示。在浮環與軸套之間形成一層極薄氣膜，這層氣膜反映了密封的潤滑性能、摩擦性能等，氣膜體現了密封的整體工作狀態，建議抽取流域進行分析，在流域中反應了槽形、偏心和結構。因此將模型導入ANSYS Workbench的DM軟件中，將浮環軸套模型四周封閉，使用Fill命令中的By Gaps進行氣膜流道抽取，抽取到的微間隙氣膜如圖3所示。

圖3 流固耦合模型及氣膜結構示意圖Fig 3 Fluid-solid coupling model and gas film structure diagram

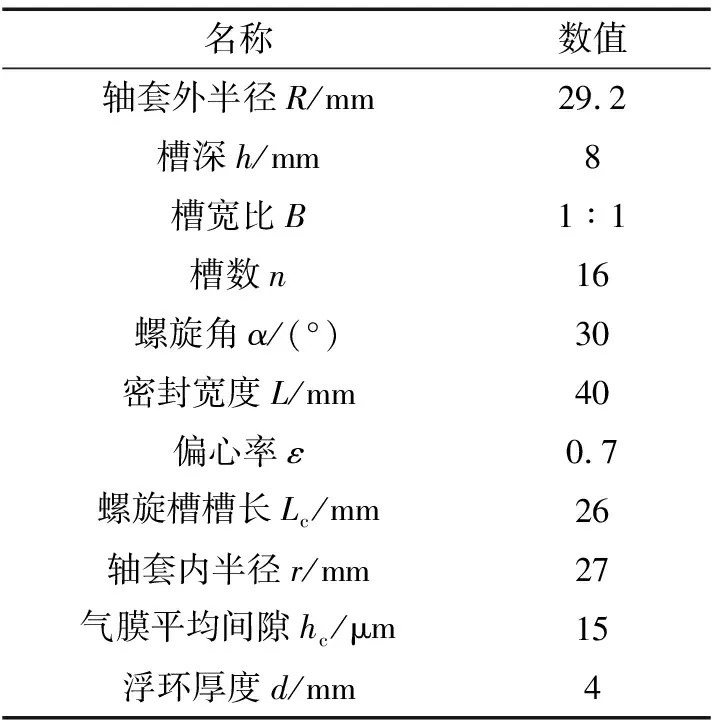
名稱數值軸套外半徑R/mm29.2槽深h/mm8槽寬比B1∶1槽數n16螺旋角α/(°)30密封寬度L/mm40偏心率ε0.7螺旋槽槽長Lc/mm26軸套內半徑r/mm27氣膜平均間隙hc/μm15浮環厚度d/mm4

2 網格的劃分及無關性驗證

2.1 網格劃分

柱面螺旋槽氣膜結構較為復雜，橫縱尺度跨度較大，并有偏心，最薄的區域只有幾微米，因此網格劃分有以下難點：

(1)有偏心,不滿足周期性規律，需整體劃分；

(2)螺旋線扭曲程度較大，為保證網格質量需進行切塊處理；

(3)螺旋槽氣膜極薄，導入ICEM后需要花費大量的時間進行幾何拓撲修補；

(4)由于模型需切224個block提高網絡精度，需要建大量的輔助線來完成Block的映射，因此，需采用ICEM結構化六面體網格方法進行劃分。

采用ICEM結構化六面體網格劃分方法雖然工作量較大，但是解決了計算過程中的不收斂問題，而且大大提高了計算精度。

具體過程如下：

(1)沿一個螺旋槽型在外氣膜上利用面建一個block，將其切成4塊，再把對應的非槽區的block拉伸出去，如圖4(a)所示。

(2)將建立好的5塊block進行旋轉處理，但是由于偏心的影響，旋轉出來的block節點之間無法對應，則需要采取合并節點處理，合并完節點的block模型如圖4(b)所示。

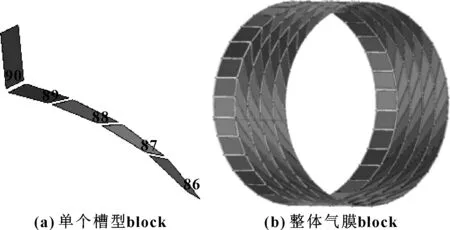
圖4 氣膜block劃分示意圖Fig 4 Block partition diagram of gas film(a)single slot block；(b)integral film block

(3)分別將槽區對應的64塊block拉伸出去與槽區的幾何進行關聯，由于模型切塊的較小，為了更好地提高網格映射質量，需要所有block的每條edge都能映射到幾何體上，因此需要對幾何體進行輔助線的建立，如圖5(a)所示。

(4)最后對block的每條edge設立合適的節點數即可生成氣膜網格，如圖5(b)所示。

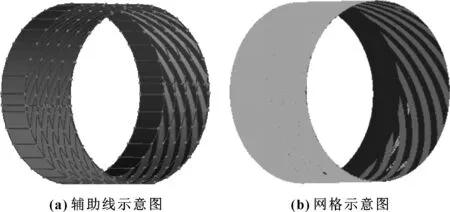
圖5 氣膜網格劃分示意圖Fig 5 Gas film mesh partition diagram (a)auxiliary line diagram；(b)grid diagram

生成的網格通過Pre-mesh Quality進行網格質量評價，結果網格質量在0.5以上且無負體積網格。

固體域浮環則采取ANSYS Workbench自帶網格劃分軟件mesh進行網格劃分。

2.2 網格無關性驗證

為了對流場域和固體域進行網格無關性驗證，現分別劃分不同的網格數，計算流場的最大壓力值和浮環最大變形。各參數對比如表2所示。

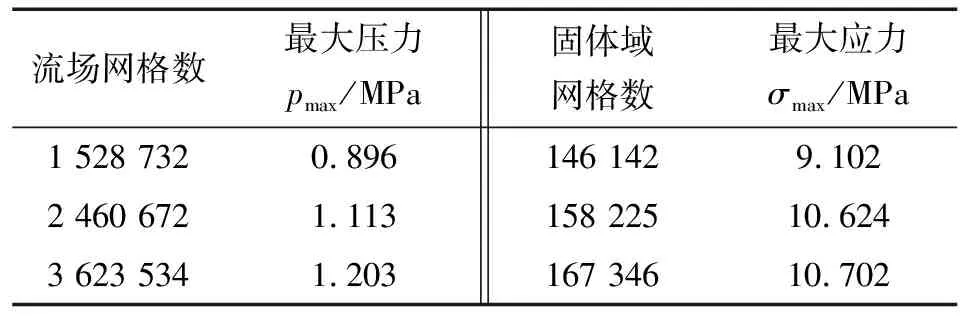
表2 網格無關性驗證計算結果

根據3種不同疏密程度的網格的計算結果，同時考慮該模型復雜性，為了在不改變計算精度的條件下，提高模擬計算的效率，縮短計算時間，文中采用的流體網格數量為2 460 672，固體域網格數量為158 225。

3 邊界條件

邊界條件如圖6所示。入口壓力為1 MPa，出口壓力為0.1 MPa，Moving-wall的轉速為30 000 r/min。采用SIMPLE算法，速度采用無滑移邊界條件。控制方程采用二階迎風離散格式。

圖6 邊界條件示意圖Fig 6 Schematic diagram of boundary conditions

4 結果與討論

4.1 氣膜的壓力和速度分析

壓力和速度矢量分布云圖如圖7和圖8所示。

由圖7可知：只有氣膜最薄區才出現了明顯的壓力上升，而在氣膜較厚的區域沒有明顯的壓力上升；同時，氣膜最薄區，隨著氣流流向槽根徑，壓力逐漸增大，并在槽根徑處壓力最大，最大壓力為1.165 MPa。由于偏心和螺旋槽的共同作用，隨著轉軸的旋轉，密封介質被泵吸到螺旋槽內，加之偏心產生的收斂不均，從而導致在氣膜最薄處產生了動壓效應。另一方面，由于槽區和非槽區存在臺階，產生節流效應，壓力逐漸下降。

由圖8可知：流體沿著逆時針方向在做周向運動；在氣膜最薄處，流速最小，壓力最大，說明能量耗散，產生明顯的壓降，從而導致了壓力在槽底部達到最大。

圖7 氣膜壓力云圖Fig 7 Film pressure clouds

圖8 氣膜速度矢量云圖Fig 8 Film velocity vector clouds

4.2 浮環強度分析

浮環材料采用的是石墨，具體材料物性參數如表3所示。

表3 浮環的材料參數

4.2.1 邊界條件確定

設置浮環邊界條件如圖9所示：浮環在與軸套同側開槽處采用fixed完全固定，FS為彈簧力，約為0.5 MPa，F為氣膜壓力，p為介質壓力。

圖9 浮環邊界條件示意圖Fig 9 Drawing of boundary conditions of floating ring

4.2.2 浮環變形

計算得到的1 MPa介質壓力下浮環變形情況如圖10所示。

圖10 浮環變形Fig 10 Floating ring deformation

可以看出：浮環的變形主要表現為沿徑向的擠壓變形，軸向變形相對來說比較小；沿著氣流流動的方向，變形量逐漸在增大；浮環的最大變形出現在浮環的外邊緣處，主要發生的是擠壓變形，最大變形量約為0.019 mm。這是因為在最大變形處流場壓力最低，流場壓力和介質壓力間較大的壓差導致嚴重的擠壓變形，最大變形量已經超過密封時平均氣膜厚度0.015 mm。可見流場的變化對浮環的變形有一定的影響，進而影響著整個柱面螺旋槽干氣密封系統的密封性能。

由圖11所示的應力分布可以看出：1 MPa介質壓力下在浮環外邊緣處，應力普遍較大，浮環的最大Von-mises應力約為10.6 MPa。浮環的材料石墨為脆性材料，抗壓強度σb=195 MPa，名義屈服強度σs=0.25σb，得σs=47.85 MPa，取安全系數nb=2.5，滿足強度要求。浮環的最大Von-mises應力主要出現了兩處：一處出現在定位銷安裝的地方，主要是因為應力集中的影響，第二處出現在浮環的最大變形處，主要是因為此處存在較大壓差。

圖11 浮環應力分布Fig 11 Stress distribution of floating ring

4.2.3 不同介質壓力下的浮環變形分析

為了研究在不同介質壓力下浮環的變形情況，現取轉速為30 000 r/min、出口壓力為0.1 MPa、彈簧力為0.5 MPa，對介質壓力為1～5 MPa下的變形和應力進行計算分析，得到的結果如圖12所示。圖中還示出了5 MPa時浮環變形情況。

圖12 不同介質壓力下浮環最大變形和應力分布Fig 12 Maximum deformation and stress distribution of floating ring under different media pressure

由圖12可知：隨著介質壓力的不斷增大，浮環的最大變形量和最大應力值呈線性增大，從1 MPa到5 MPa介質壓力每增加1 MPa最大變形量增幅分別為50%、34%、25%、20%。對比圖12和圖10，隨著介質壓力不斷增大，浮環大變形的范圍在逐漸擴大，最大變形由一處變為兩處，且逐漸變為沿整個流體出口的方向都受到大變形擠壓。此時由于浮環的大變形已經超過了密封時最厚氣膜厚度0.025 5 mm，很容易導致旋轉的軸套被卡死再無法進行運轉，同時導致浮環和轉軸之間產生嚴重的磨損，甚至引起浮環碎裂等惡劣影響，因此，浮環的大變形嚴重影響了柱面密封系統的穩定性和密封性能。

4.2.4 不同轉速下的浮環變形分析

為了研究在不同轉速下浮環的變形情況，現取介質壓力為1 MPa、出口壓力為0.1 MPa、彈簧力為0.5 MPa，計算了30 000、50 000、70 000、90 000 r/min 4組轉速下的浮環變形和應力，結果如圖13所示。

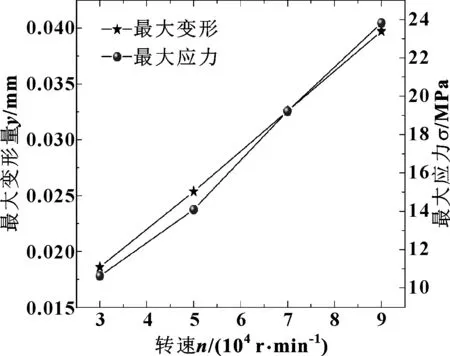
圖13 不同轉速下浮環最大變形和應力分布Fig 13 Maximum deformation and stress distribution of floating ring at different rotational speed

由圖13可知：隨著轉速的不斷增大，浮環的最大變形量和最大應力值不斷增大。從圖12可看出，介質壓力每增加1 MPa，變形量至少約增加0.01 mm，而從圖13可看出轉速每增加20 000 r/min，變形量約增加0.007 mm。可見浮環的變形主要受介質壓力的影響，而轉速的影響相對較小。這是由于，密封的變形主要是力變形，而轉速只能影響氣膜壓力的變化，無法直接改變密封的腔體壓力，因此密封系統的變形主要來自于介質壓力。

5 結論

(1)在氣膜最薄區的動壓效應最為明顯，同時臺階產生的節流效應，導致出口的壓力下降趨勢明顯大于從氣流入口到螺旋槽根徑的壓力上升趨勢。

(2)浮環的變形主要表現為沿徑向的擠壓變形，軸向變形相對來說比較小。最大變形出現在流場壓力最小的地方。

(3)隨著介質壓力、轉速的不斷增加，浮環的最大變形量及應力值也呈線性規律增大，而且最大變形主要受介質壓力的影響。

(4)文中只考慮了力對浮環變形的影響，然而在密封腔內由于氣體攪拌和黏性剪切會產生大量的熱，因此還需考慮熱對變形的影響，這將是下一步研究的方向。