多尺度視角下裝備維修經費序列波動特征與事件影響分析

蔣鐵軍， 張懷強， 周成杰

(海軍工程大學管理工程與裝備經濟系，湖北 武漢 430033)

裝備維修保障工作受到各種內在和外在因素的影響，這些影響的顯性表現形式多種多樣，反映到經濟層面主要是裝備的維修經費，且在不同時期這些因素的影響具體體現為維修經費序列的波動。裝備維修經費序列通常呈現出顯著的非線性、非平穩性和多尺度等特性，尤其是各類事件的影響，如：等級修理、各類演習訓練任務、現代化改裝，以及經濟環境的劇烈波動等，往往還會使經費序列產生結構突變，使傳統經費預測和決策模型的適應性顯著變差，分析難度加大[1]。隨著裝備執行多樣化軍事任務的頻率和強度不斷增加，以及經濟環境的動態變化，各類事件對裝備維修經費的影響將愈加顯著。

通過分析裝備維修經費序列隨時間推進的波動特征，有效地識別經費序列的結構性變化，能夠在一定程度上了解各種因素的影響變化以及事件的影響情況，為開展相關預測和決策分析提供基礎支撐。

裝備維修經費序列是一類典型的經濟時間序列。傳統的時間序列波動特征和事件影響分析方法通常直接針對序列本身展開，由于時間序列影響因素及其構成的復雜性，效果往往不是太好。隨著多尺度分析方法的不斷提出，從多尺度視角辨識時間序列的有效構成，在不同尺度上分析分量序列的發展變化規律是目前采用較多的一種處理辦法[2]。對時間序列進行多尺度分析，關鍵是要對序列進行有效的多尺度分解。傳統的序列分解方法主要有傅立葉譜分析、小波分析等[3-4]，這些方法的優勢在于可以很好地處理非平穩、非線性信號，且直觀、簡單，但也存在一定的不足，如：傅立葉譜分析在時域內不具有分辨率，小波變換不能實現自適應多分辨率分析等[5]。ZHU等[6]提出的經驗模態分解(Empirical Mode Decomposition，EMD)算法可以基于原始時間序列的局部特征，直接提取出一種固有模態函數(Intrinsic Mode Function，IMF)，進而實現序列的自適應分解。相對于傳統分解方法，其具有更強的原始特征和局部特性識別能力，是目前開展時間序列多尺度分析的較好方法之一[7]。

在事件對時間序列的影響分析方面，通常采用檢驗方法識別序列中的結構變點，如：Chow檢驗[8]、Quandt-Chow檢驗[9]、BP檢驗[10]、CUSUM-SQ檢驗[11]等。其中，INCLAN等[12]基于中心化累積平方和方法，改進性提出了迭代累積平方和(Iterative Cumulative Sums of Squares，ICSS)算法，用于尋找序列在不同時點的突變點，該算法能實現序列中多個結構性方差變點的識別，且簡便易行、效果較好，已被廣泛應用于解決各類時間序列的變點識別問題[13-14]。

鑒于EMD算法在序列分解上的優異性能以及ICSS算法在序列結構變點檢驗中的良好表現，筆者集成二者的優勢，提出了多尺度視角下的裝備維修經費序列波動特征與事件影響分析方法。首先采用EMD算法對原始經費序列進行多尺度分解，獲取其基本構成、波動特征和各類因素的影響情況，然后針對每個分量，分別采用ICSS算法進行結構變點識別，從深層次揭示裝備維修經費序列的波動特性，以及事件對經費序列內在結構變化的影響。

1 經費序列分量波動特征分析指標選取

由于裝備維修經費的不同IMF的發展變化趨勢可能存在較大差異，筆者主要通過統計分析方法對不同IMF進行波動特征分析。采用的統計指標主要有IMF的平均周期(平均周期)、IMF的方差及其相對于原始經費序列的方差占比(方差貢獻率)、IMF與原始經費序列的Pearson系數和Kendall系數[14]。各項指標的具體含義如下：

1) 平均周期。周期是時間序列波動的典型特征之一。由于原始經費序列經EMD算法分解后，各IMF的頻率往往會隨時間變化，因此，應采用平均周期描述各IMF的頻率變化情況，即

T=2L/s。

(1)

式中：T為IMF的平均周期；L為IMF的長度；s為波峰和波谷的數量。

2) 方差貢獻率。EMD分解的目的之一是分析不同尺度分量對總體經費序列變化的影響。由于各IMF彼此基本相互獨立，因此，可以利用方差占比描述各IMF對原始經費序列的貢獻度，即

(2)

3) 相關系數。相關系數用于衡量各IMF與原始經費序列之間的相關性。Pearson系數和Kendall系數主要用于衡量數量相關和等級相關[15-16]，其中

Pearson系數的計算公式為

(3)

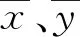
Kendall系數的計算公式為

(4)

式中：ωij=(xj-xi)(yj-yi)。

對于任意給定的數據對(xi,xj)和(yi,yj)，若(xj-xi)(yj-yi)>0，則二者等級一致;否則,不一致。

2 經驗模態分解

EMD認為時間序列是由不同尺度上的基本分量(IMF)構成，通過分解可以實現序列的平穩化，同時可將序列原本的構成特征展示出來。

該算法的基本實現步驟如下[15]：

1) 對任一給定時間序列s(t)，確定其所有極值點；

2) 根據極值點用三次樣條曲線作上下包絡線；

3) 計算包絡線均值m11(t)，得到該序列與均值之差h11(t)=s(t)-m11(t)；

4) 將h11(t)視為s(t)，重復步驟1)-3)，若h1(k-1)與h1k的方差小于某值，則h1k為1個IMF，此時c1=h1k，r1(t)=s(t)-c1；

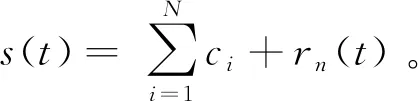
3 迭代累積平方和

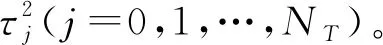
Dk=Ck/CT-k/T，

(5)

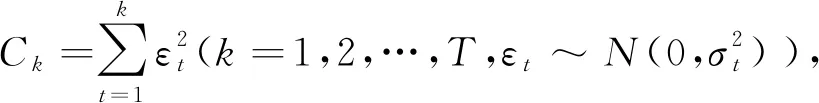
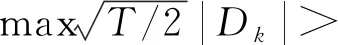
4 經費序列波動特征與事件影響分析框架

多尺度視角下的裝備維修經費序列波動特征與事件影響分析框架如圖1所示。

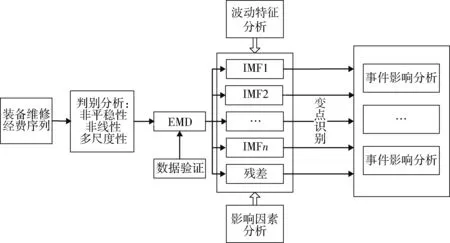
圖1 裝備維修經費序列波動特征與事件影響分析框架

具體分析步驟如下：

1) 原始經費序列判別分析。將統計檢驗和經驗分析相結合判別原始經費序列的基本特性。

2) 原始經費序列多尺度分解。運用EMD算法對原始經費序列進行分解，從多個層面更加細致地研究原始經費序列的發展變化規律。

3) 經費序列分量波動特征及影響因素分析。計算不同IMF的統計指標，分析經費序列的波動特征以及不同因素對不同IMF的影響。

4) 經費序列分量變點識別。通過對變點統計檢驗和現實事件影響的對比分析，確定經費序列結構發生重大變化的時間點。

5) 事件影響分析。比較分析變點前后經費序列分量統計特征的變化，判別事件對經費序列的影響，結合背景知識，分析事件類型及其對經費序列的影響機理。

5 應用分析

5.1 數據獲取

艦船維修器材經費由于受器材故障規律、裝備使用強度、管理模式，以及各種事件(如臨時檢修、人員誤操作、等級修理、現代化改裝)等多重因素的影響，其序列表現出較強的非線性、非平穩和多尺度等特性[16]。

因此，筆者以某型艦船裝備維修器材經費數據為對象開展應用分析。

5.2 原始經費序列判別分析

采用ADF(Augmented Dickey-Fuller)方法判別原始經費序列的非平穩性，計算得到在顯著性水平1%、5%和10%下的臨界值分別為-2.590 7、-1.944 4和-1.614 1，序列的統計量為1.302 7，P值為0.950 5，表明原始經費序列具有非平穩性，該序列可能包含趨勢、季節性或周期性等成分，這一特征比較符合裝備故障的一般規律以及計劃籌措與臨時籌措相結合的常規做法。

采用BDS(Brock,Dechert & Scheinkman)方法判別原始經費序列的非線性[17]，計算標準差分別為0.5、0.75、1、1.25和1.5，嵌入維數從2到10的BDS統計值，具體如表1所示。從表1可以看出：BDS統計值均大于顯著性水平為5%時的臨界值(1.96)，表明原始經費序列具有非線性，這一特征也進一步驗證了經費受到多重因素的影響，且相互之間存在著較為復雜的非線性關系。

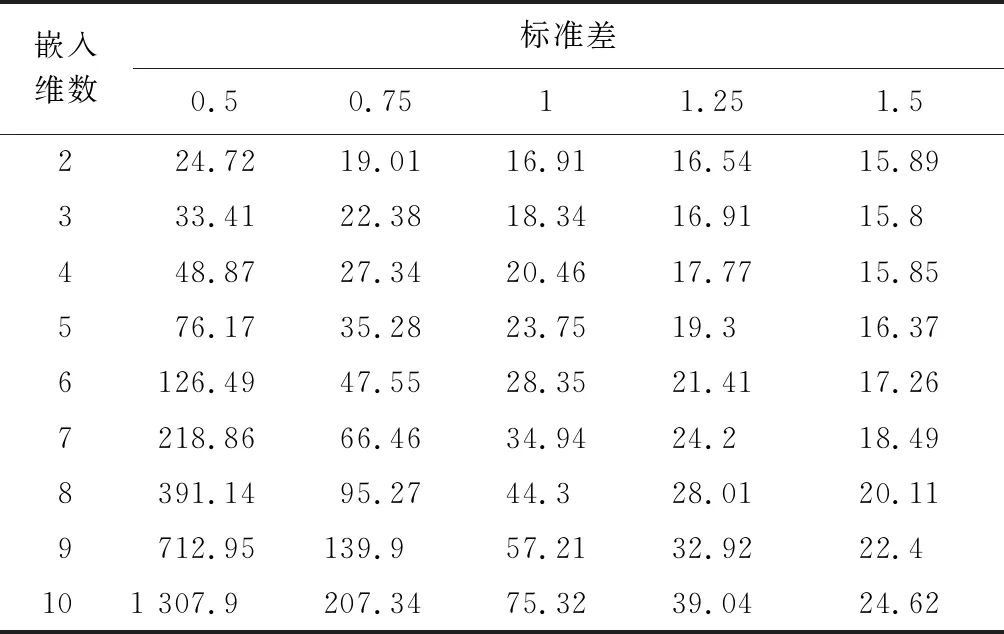
表1 原始經費序列的BDS統計值

對于原始經費序列的多尺度性，根據器材經費受隨機性故障、裝備使用強度、管理模式以及各種事件對經費序列產生影響程度的不同，可初步判定經費序列具有多尺度性。該特性也將結合序列分解進一步得到驗證。

5.3 時間序列分解

EMD算法對原始經費序列分解的具體情況如圖2所示。從圖2可以看出：1)原始經費序列被分解成了4個IMF，不同IMF具有不同的頻率水平；2)IMF的振幅和頻率負相關，即頻率越高，振幅越小；3)IMF4(殘差序列)去除了高頻波動，基本維持了原始經費序列的趨勢水平；4)原始經費序列具有明顯的多尺度性，通過序列分解，能夠更加細致地觀察經費序列的發展變化規律。

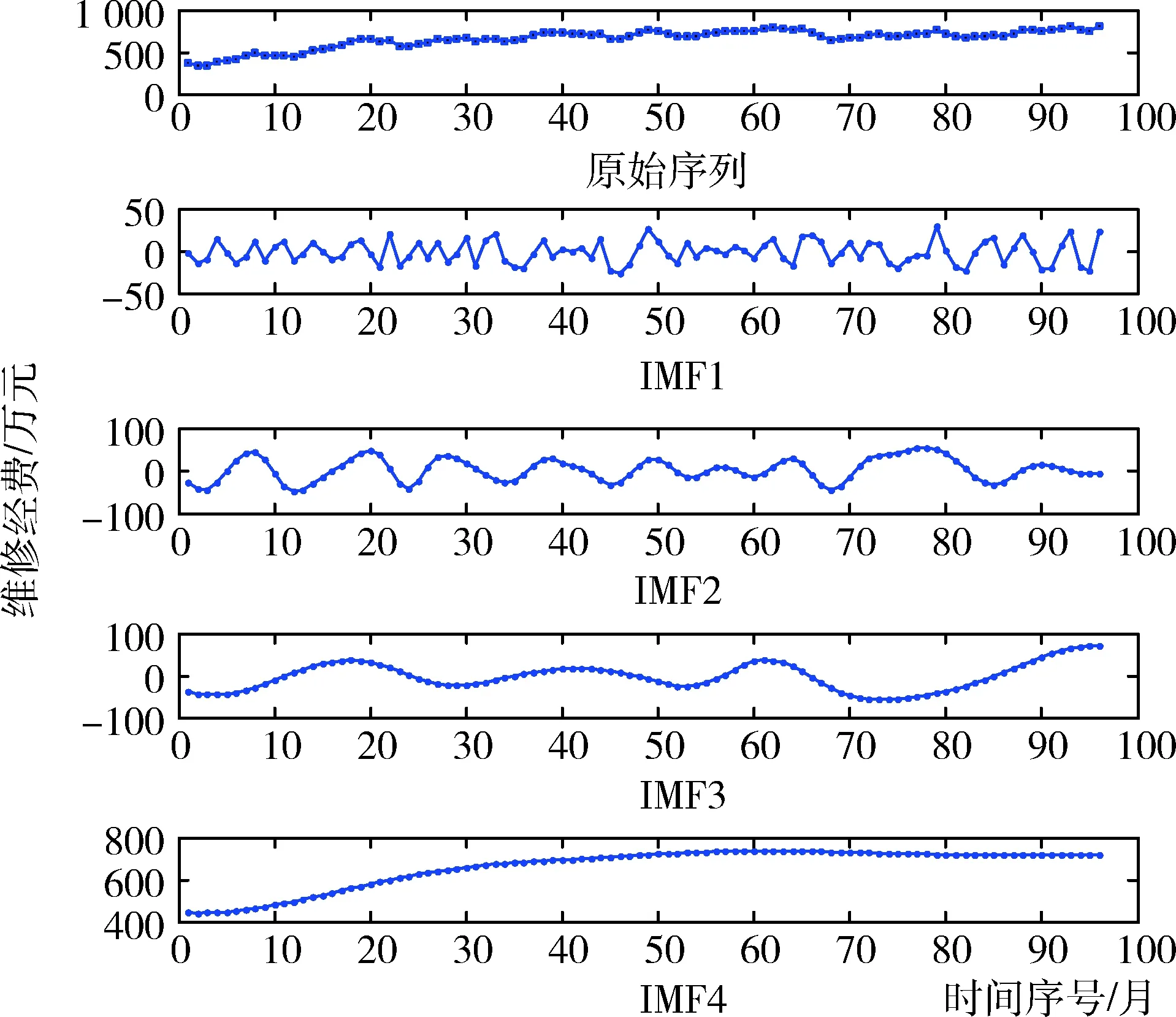
圖2 基于EMD算法的原始經費序列分解

5.4 經費序列分量波動特征與影響因素分析

5.4.1 經費序列分量波動特征分析

通過對不同IMF和原始經費序列的統計計算，可以得到如表2所示的相關統計指標值。

從平均周期看，IMF1、IMF2的平均周期分別為3.6月和10.1月，均在1 a以內，相對較短，是典型的高頻序列，其振幅集中在55以內；IMF3的平均周期較IMF2、IMF1有所加長，約2 a左右，屬低頻序列，振幅也略有增加；殘差序列無明顯周期性，大約自第10月開始，呈先快速上升后逐漸趨于平緩的態勢，與原始經費序列的發展趨勢大體一致。表明經費的周期性變化主要受到裝備戰訓任務、等級修理周期等因素的影響，但長期發展趨勢仍以裝備故障規律的影響為主。

表2 不同IMF的統計指標值

從方差貢獻率看，殘差分量對原始經費序列走勢影響最明顯，達到82.16%。各IMF的貢獻率隨頻率水平的增加而減小，如IMF1的貢獻率僅為1.68%。

從相關系數看，基本規律與方差貢獻率類似。殘差分量與原始經費序列的相關程度最為顯著，Pearson、Kendall系數分別為0.928 5和0.580 1。其他IMF隨著頻率水平的增加，其相關程度逐步降低。表明經費的總體變化主要受到裝備故障規律等低頻分量的影響，隨機性、突發性故障等高頻分量的影響會隨著頻率增加而逐漸減弱。

5.4.2 經費序列分量的影響因素及其影響機理

通過上述統計分析，可以大致看出不同IMF的基本變化規律及其與原始經費序列的相互關系，這些規律是各種因素綜合影響的具體體現。

1) 高頻分量(IMF1、IMF2)。高頻分量的波動幅度不大、頻率高、規律性差，對經費序列的長期趨勢影響不大，如制訂維修器材中長期籌措規劃時，往往可以忽略這一影響；但短期影響則較為顯著，是制訂季度或月度器材籌措計劃需重點考慮的內容。

根據艦船裝備管理工作的具體實際，維修器材經費在短期內主要受到裝備隨機故障及不確定事件的影響。在艦船的日常使用中，往往存在著一些不可預知的事件，如：各類設備的隨機性、突發性故障，人員操作存在偶然的失誤等，這些都使得維修器材需求在短期內發生變化，且具有一定的隨機性和跳躍性。這些事件的特點是發生較為頻繁、持續時間相對較短，其對經費序列的影響主要體現在IMF1、IMF2這樣的高頻分量中。

2) 低頻分量(IMF3)。低頻分量的變化介于趨勢分量和高頻分量之間。低頻分量與原始經費序列的形態具有一定的一致性，尤其是在序列發生劇烈變化的時間點，往往對應著重要的事件。在低頻分量中，序列受事件影響后，其變化趨勢會產生較大波動，雖然短期內有一定緩和，但還是會持續較長時間。IMF3的平均周期約為2 a，說明了在沒有其他重要因素干預的情況下，分量序列在短期內難以自行消除事件的影響。

此外，低頻分量在很多時點的振幅都在原始經費序列的8%左右，平均變化量占原始經費序列的比例為4%，說明事件對原始經費序列的影響程度也是比較大的。從目前的艦船維修保障現狀來看，主要原因在于事件對裝備維修保障系統造成了重要影響，使維修保障系統的內外部環境發生了重要變化，進而對經費變化規律產生了重要影響。

3) 趨勢分量(IMF4)。趨勢分量表現了原始經費序列的長期走勢，與其具有很強的相關性，可以為今后經費預測提供基本參考。從原始經費序列的發展趨勢可以看到：雖然在某個時間點會由于某些因素的影響產生波動，但當影響消退后，還是會回歸到基本趨勢。趨勢分量體現了原始經費序列的基本走向，體現出經費受到內、外多種因素綜合作用的結果，表現為相對固有的發展規律。

趨勢項總體呈上升態勢，這與艦船維修保障的基本規律是一致的。隨著艦船入役時間的不斷延長，系統設備的老化不斷加劇、故障率不斷增加，維修器材的價格也在不斷攀升，這些內在、外在因素基本決定了維修器材經費的上升趨勢。雖然期間可能會對部分系統設備進行更新換代，其故障率在短期內有所緩和，維修經費會出現下降，但是經過一段時間之后，基本的上升趨勢同樣會繼續保持下去。

需要注意的是，某些重大事件可能對經費序列的趨勢項產生根本的結構性影響，如：大規模的改換裝工程，由于裝備配置的根本性改變，系統設備的故障規律會發生本質變化；維修經費的構成內容重新進行了調整，維修經費計算執行了新的規范，維修經費的統計計算結果也將會發生實質性變化。

5.5 經費序列分量的變點檢驗

采用ICSS算法分別對原始經費序列和各分量序列進行變點檢驗，結果如表3所示。

由表3可以看出：1)原始經費序列、IMF1、IMF2均無變點，即事件未對這些序列的結構趨勢產生影響；2)IMF3的結構在第22月和69月發生突變，變點前后序列的趨勢發生了較大變化，但是原始經費序列轉折點與變點并不完全一致，主要是因為事件影響往往是在相對較短的時期內不斷顯現出來，如圖3所示；3)IMF4也無變點，與原始序列一致，表明事件還未強烈到影響經費序列的基本趨勢；4)原始經費序列無變點，但IMF3有變點，進一步表明從多尺度視角研究裝備維修經費序列波動特征和事件影響的必要性。

表3 ICSS算法變點檢驗結果(置信度95%)

5.6 事件對經費序列分量的影響分析

采用對變點前后序列進行統計的方法，分析事件對IMF3產生的影響。

5.6.1 變點1的影響分析

第1個變點前后數據序列的統計結果如表4所示，可以看出：分量序列的方差變小、振幅均值變小，說明經過事件后，序列的波動幅度呈現相對平緩的趨勢。主要原因是裝備經過局部改裝，部分設備換代升級，故障規律相應發生變化，且故障率降低。但由于改裝初期的磨合問題，故障率會短期內小幅波動，隨后一段時間內總體降低且呈現平穩態勢。

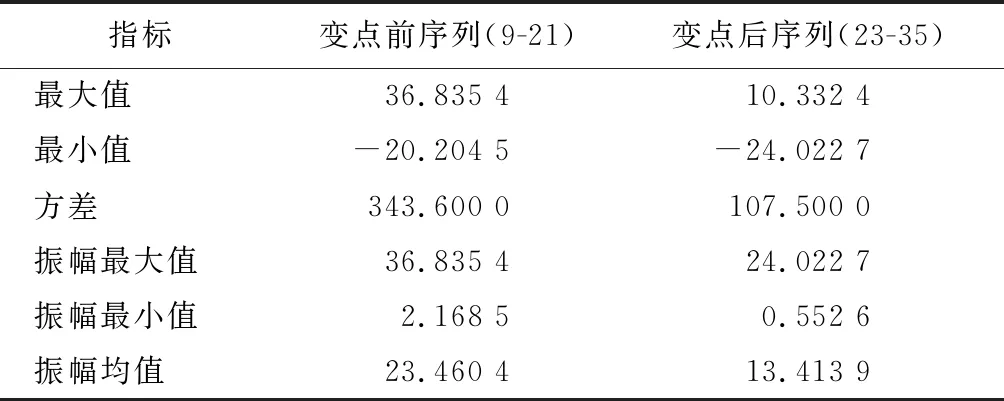
表4 變點1前后數據序列的統計情況

5.6.2 變點2的影響分析

第2個變點前后數據序列的統計結果如表5所示，可以看出：分量序列的最大值變大、最小值變小、方差變大、振幅均值變大，說明經過事件后，分量序列的波動在不斷增大。主要是因為裝備使用強度增加使故障率增大。但事件發生后短期內，器材消耗有所降低，主要是在事件點開展了等級修理，裝備技術狀態得到一定程度的恢復，但隨著使用強度的持續加大，序列隨后出現大幅波動。

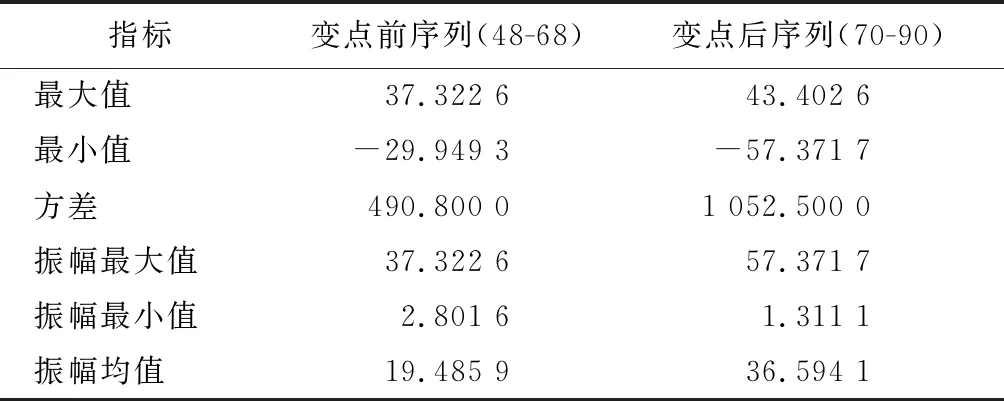
表5 變點2前后數據序列的統計情況

6 結論

筆者主要針對裝備維修經費序列表現出的非線性、非平穩性、多尺度等特性，運用EMD算法對其進行分解，進而從多尺度視角對經費序列開展波動特征和事件影響分析。結果表明：

1) 裝備維修經費序列主要受到自身發展趨勢、各類事件和隨機故障等多重因素的影響，具體體現在分解后的不同尺度序列上；

2) 不同因素對原始經費序列的影響效果不盡相同，自身發展趨勢體現了經費序列的基本內在規律，事件影響著經費序列在較長一段時期的劇烈波動，而隨機故障則使經費序列產生不規則的短期波動；

3) 針對EMD算法分解后的經費序列分量開展變點檢驗，相對于直接針對原始經費序列的檢驗更加有效，表現出更強的辨識能力；

4) 識別出的經費序列分量變點，與現實情況基本一致，進一步驗證了方法的有效性和可靠性；

5) 通過對變點前后數據序列變化情況的統計分析，基本符合對現實事件分析得出的一般規律。