軸向循環加載卸載條件下飽和軟土變形特性試驗研究

王學營， 岳夏冰， 惠 冰

(1.內蒙古自治區交通建設工程質量監督局， 內蒙古 呼和浩特 010020； 2.長安大學 公路學院， 陜西 西安 710064； 3.中交通力建設股份有限公司， 陜西 西安 710075)

1 研究背景

隨著我國經濟的快速發展，城市交通基礎設施建設也相繼迅速發展。高層超高層建筑、高速公路和鐵路工程、橋梁隧道工程、地鐵和越江隧道工程、地下商場、水電站、大型油罐等相繼修建。而這些工程必然要穿越或修建在軟土之上，并且經常承受著變載的作用，因而卸載作用隨之可見。從大量的工程實際和試驗研究表明，軟黏土具有明顯的流變性，軟黏土變形和強度特性與其應力狀態以及加載歷史密切相關，巖土材料在外荷載下所產生的塑性變形是不可逆的。循環加卸載造成的變形將會不停累積并決定最終變形。

受應力歷史影響，每經歷一個加卸載，其再加荷所產生的變形將明顯小于前次。這也是為什么同荷載下超固結土所產生的變形明顯小于正常固結土的原因。

“加荷-卸荷-再加荷”這種加荷方式就是通過荷載的循環模擬土的應力歷史。

與普通的單軸及三軸試驗相比，加卸載試驗更能揭示土的力學特征，因而研究循環加卸載條件下軟黏土的強度和變形特性具有一定的工程實踐價值[1-2]。目前關于循環荷載條件下巖土體變形特性的研究也比較多，但大多數是循環三軸試驗，而在K0狀態下一維固結軸向循環加卸載試驗研究目前還較少[3-4]。

本文依托實體公路工程。由現場取樣，通過利用長安大學自行研制的連續加載K0固結儀，對所取一定深度飽和土開展循環加卸載試驗，分析其在整個試驗過程的變形特征和在整個加卸載過程中土體彈、塑性變形與應力水平的關系，建立了相應的表達式，以便于工程實際應用。最后根據試驗結果建立了循環加卸載本構方程[5-7]，并對塑性滯回能進行計算擬合。

2 循環加卸載試驗

此次飽和軟黏土循環加卸載試驗采用長安大學自行研制的一維側限固結儀。該試驗儀器由三軸加荷裝置進行加荷，由固結儀上的傳感器觀測試驗過程中的軸向應力、側向應力、軸向位移和孔隙水壓力，并通過數據儲存系統記錄試驗數據。

本試驗土樣采用武漢地區軟土，呈灰色，軟塑狀態，有機質含量較多，試樣為圓柱體狀，尺寸為高40 mm、直徑61.8 mm，塑限wp=31，液限wl=59，塑性指數IP=28。該試樣采用真空飽和氣進行飽和，具體飽和過程為：將制備好的試樣放入飽和缸內，封蓋前用凡士林進行密封，確認密封完好后開始抽真空。當真空壓力表值達到0.01，打開連通飽和缸的水管，向其內注水，直至試樣被水覆蓋2～3 cm時，停止注水并繼續保持抽氣機抽氣10～15 min，最后打開空氣閥。靜置24 h后即可。飽和后土樣的飽和度Sr=99%，ρ=1.69 g/cm3，e0=1.44。試樣飽和后進行循環加載卸載試驗。飽和試樣制備完以后將試樣放入固結儀內，試驗首先在完全側限條件下對土樣進行連續加載。先對試樣施加1 kPa的預壓力，并將測試傳感器均歸零。采用0.002 4 mm/min的加荷速率。對試樣施加軸向應力，定時采集數據。當達到第1級應力水平后在同樣速率下進行卸載。當軸向應力水平卸載為0后，再對土樣實施第2級荷載，達到第2級應力水平后再次卸載，直至最后1級荷載。試驗結束，關電源，拆除儀器，取出試樣。試驗共設5級等增量加載、卸載，如表1所示。利用位移傳感器量測土樣達到相應應力水平時的總應變以及軸向荷載卸載為0時土體的殘余應變。

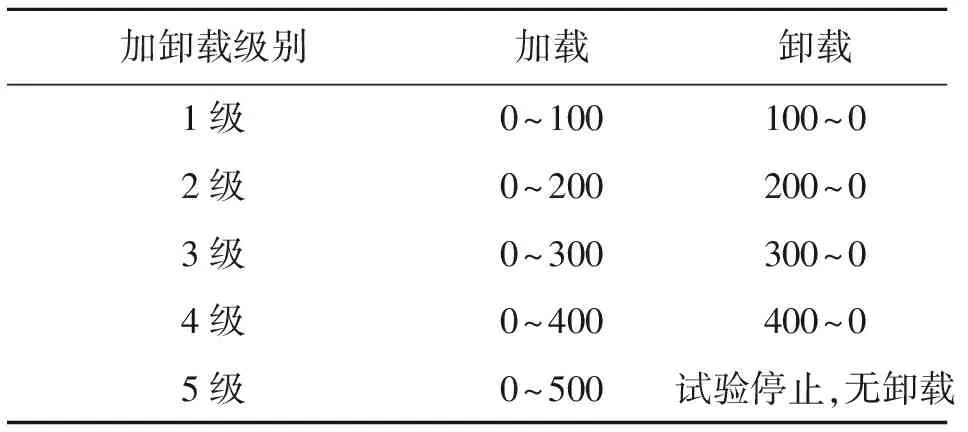
表1 循環加、卸載試驗方案 kPa

3 加卸載試驗數據分析及本構關系

3.1 試驗數據分析

3.1.1 軸向應力與軸向應變關系圖 本文以2級循環加卸載對軸向應力與軸向應變關系進行說明，如圖1所示。圖中L1為初始加載曲線，L2為卸載曲線，L3為再加載曲線，L4為第2級卸載曲線，4個曲線對應的初始變形模量分別為En1、Em1、En2、Em2、；卸載頂點為A(ε1，σ1)和B(ε2，σ2)，εp1、εp2為卸載過程軸向應力為零時所對應的應變，即為試樣的塑性變形；σn1、σn2為加載階段軸向應變趨于無窮大時對應的最大軸向應力；εm1、εm2為卸載曲線軸向應力趨于無窮大時的最大軸向應變。

由圖1可以看出，試驗加載過程體積減小，卸載曲線及加載曲線坡度均與加載曲線的起始坡度相等。在再加載曲線的最后階段，即再加荷載超過前次卸載值后，其對應的曲線將保持原單軸加載曲線同一路徑繼續上升，相關學者定義為巖土材料的變形記憶[4]。在卸載和再加載曲線之間形成了一個封閉的滯回環，土體的應變既有不可恢復的塑性應變又有可以恢復的彈性應變。初始切線模量是由初始加載曲線計算所得，回彈模量則由卸載曲線確定，其均可用于沉降分析與計算。由圖1可見，任一加卸載循環曲線，相等的應力增量所對應產生的應變增量不等，初始加載曲線所對應的應變增量值明顯大于再加荷曲線，這也說明了土體的應力歷史對變形是有影響的[5]。

3.1.2 卸載曲線分析 軟土在K0狀態下各級卸載曲線的軸向應力與軸向應變曲線如圖2所示。

圖2顯示，各級卸載曲線的變化趨勢是相同的，卸載初期曲線的變化趨勢較陡，可近似為直線；而隨著卸載時間不斷增加，卸載為曲線形式。而卸載曲線主要是由曲線段構成的，這也說明了飽和軟土的非線性特性，這是與巖石卸載曲線不同的。通過卸荷曲線可以求得飽和軟土的變形模量以及土體的塑性變形。隧道圍巖長期處于卸載環境中，通過得到K0狀態下的卸載曲線，在建模計算時采用卸載曲線的變形模量更接近于實際工程。

3.1.3 再加載曲線分析 圖3為飽和軟土K0狀態下循環再加載各階段對應的軸向應力與應變曲線。由圖3可見，各階段曲線前期至上級卸載值均近似為衰減形曲線，各階段曲線后段，即超過上級卸載值時，所有再加載曲線均近似為直線形，且均保持初始加載曲線同一路徑上升。對于非飽和土或一般的地基土，其加卸載曲線與初始加載曲線的起始切線斜率大致相等，但本試驗研究的為飽和軟土，其所對應的兩者間曲線斜率相別明顯，此差異的產生是由于加卸載影響了飽和軟土的物理力學特性所致，同時也表明飽和軟土的彈性變形較小。一般用再加載曲線的切線斜率表示各級再加載的變形模量，以各級再加載曲線的變形模量的平均值描述再加載曲線的變形特征[3]。

在施工過程中，地基土處于加載卸載再加載狀態，且當上覆壓力小于地基土的初始應力時，為最大程度接近與實際工程，則在數值計算中，建議選用K0狀態下再加載曲線的變形模量。

3.1.4 彈性應變與塑性應變變化規律分析 在飽和軟土加卸載曲線上可以求得試樣在各級卸載為零時的彈性變形和塑性應變，結合試驗結果與理論分析，分別將彈性應變和塑性應變隨各級卸載載荷的變化規律進行分析，如圖4、5所示。

從圖4、5可以看出，飽和軟土在循環加卸載試驗中試樣的彈性應變與塑性應變都是隨著卸荷等級的增大而增大的，但塑性應變的變化率高于彈性應變變化率，因次飽和軟土具有一定的強度，且兩者都與卸荷應力水平呈良好的線性關系，可用下列回歸方程表示：

(1)

(2)

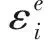
公式(1)、(2)分別表示該試樣在一維K0狀態下循環加卸載試驗得到的彈性變形和塑性變形，對以后工程實際計算土的彈塑性變形時有一定的參考價值。

3.2 加卸載的本構關系

3.2.1 本構方程推導 在軸向循環加卸載應力-應變關系曲線中，通常取曲線上軸向力為0時所對應的切線斜率作為加載或卸載過程中試樣的軸向初始變形模量Eni，用該模量確定雙曲線方程，前一級加載曲線和卸載曲線確定下一級卸載曲線和再加載曲線的初始變形模量[6-9]，從而建立循環加卸載過程的本構方程。

根據試驗結果(圖1～5)可得，加載曲線L1方程用雙曲線方程可表示為：

(3)

公式(3)也可用下式表示：

(4)

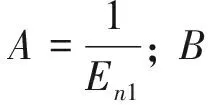
因此公式(3) 可以變為：

(5)

整個加載曲線L1的變形模量可以寫為[6]：

(6)

卸載曲線L2的方程可以寫為：

(7)

由于A點在卸載曲線上，將A點的坐標代入公式(7)可以得到：

(8)

卸載曲線軸向應力為零時對應的變形模量可通過試驗求得：

(9)

卸載曲線上軸向應力趨于無窮大時的軸向應變可表示為：

(10)

將公式(9)、(10)代入公式(7)，可求出C和D：

C=Em1

(11)

(12)

將公式(11)、(12)代入公式(8)中整理后可得到方程式：

(13)

求解方程(13)可得到：

(14)

根據公式(14)可以求得卸載為零時試樣的變形量，即試樣的塑性應變。

將公式(11)、(12)代入公式(7)中，可以得到卸載曲線應力表達式：

(15)

卸載過程的變形模量可表示為：

(16)

根據同樣方法可以求得再加載曲線L3的應力表達式以及變形模量表達式為：

(17)

(18)

根據上述方法可將飽和軟土循環加卸載的應力-應變方程及變形模量表述出來：

初始加載曲線：

(19)

卸載曲線：

(20)

(21)

再加載曲線：

(22)

(23)

式中：i=1,2，…,n。

公式(19)～(23)即為飽和軟土循環加卸載曲線的本構方程及變形模量的表達式，式中的Eni,Emi,εp(i-1),εmi,σni參數均可在常規固結儀中的循環加卸載試驗中得到，通過施加的軸向應力可以算出所對應的某一時刻的軸向應變。

3.2.2 本構方程驗證 上述公式(19)、(20)、(22)為飽和軟土循環加卸載試驗的本構方程，方程中的參數為Eni、Emi、εp(i-1)、εmi、σni，可通過常規循環加卸載試驗得到，將這些參數整理如表2所示。

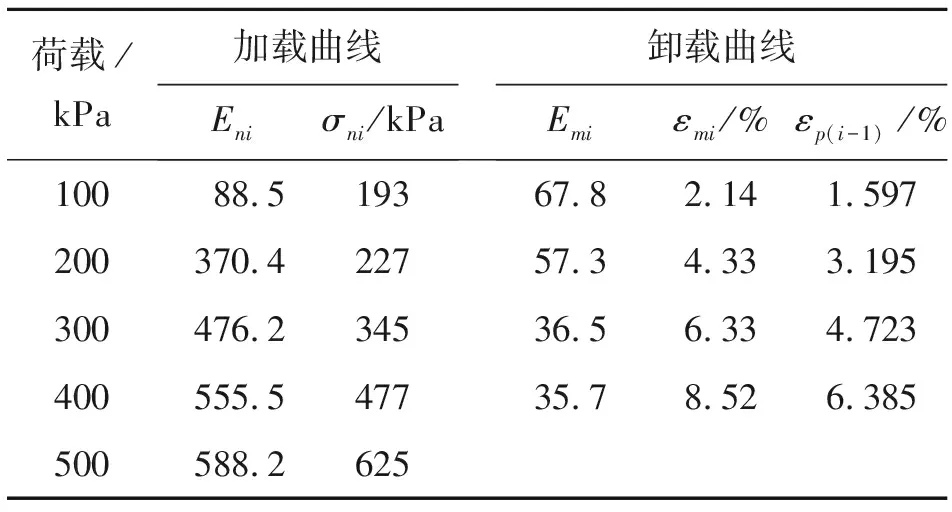
表2 本構方程各參數

將表2中的各參數代入公式(19)、(20)和(22)中，可求出循環加卸載任意軸向應力所對應的軸向應變，將本構方程計算結果與試驗數據進行了對比分析，如圖6所示。

從圖6可以看出，本構方程計算的結果與試驗結果雖然存在一定的差異，但總體的變化趨勢是相同的，說明該本構方程能夠用來描述飽和軟土的循環加卸載特性。

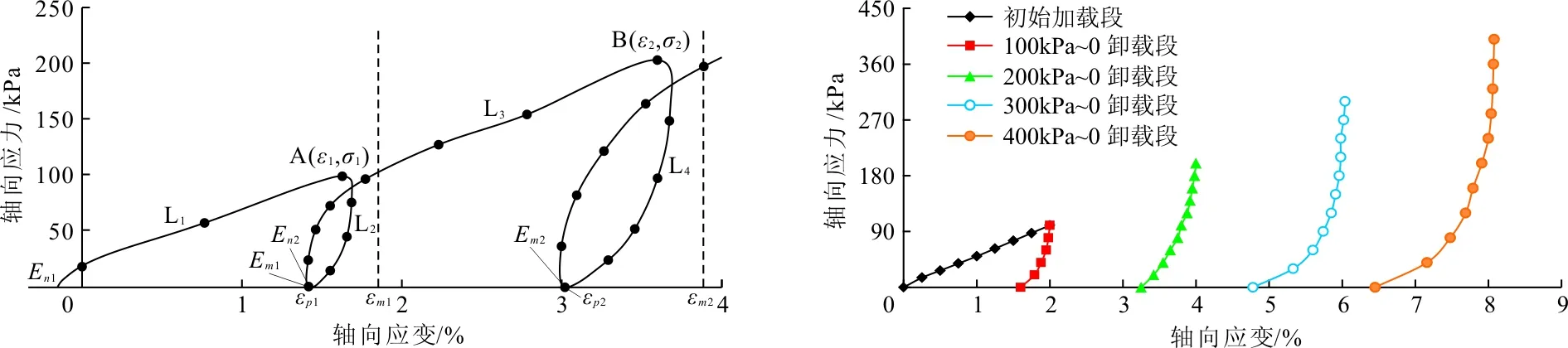
圖1軟土土樣軸向應力與軸向應變關系 圖2軟土土樣卸載曲線軸向應力與軸向應變曲線

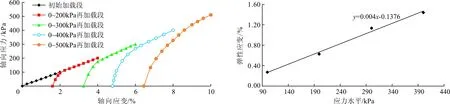
圖3軟土土樣再加載曲線軸向應力與軸向應變關系 圖4軟土土樣彈性應變與卸載載荷關系

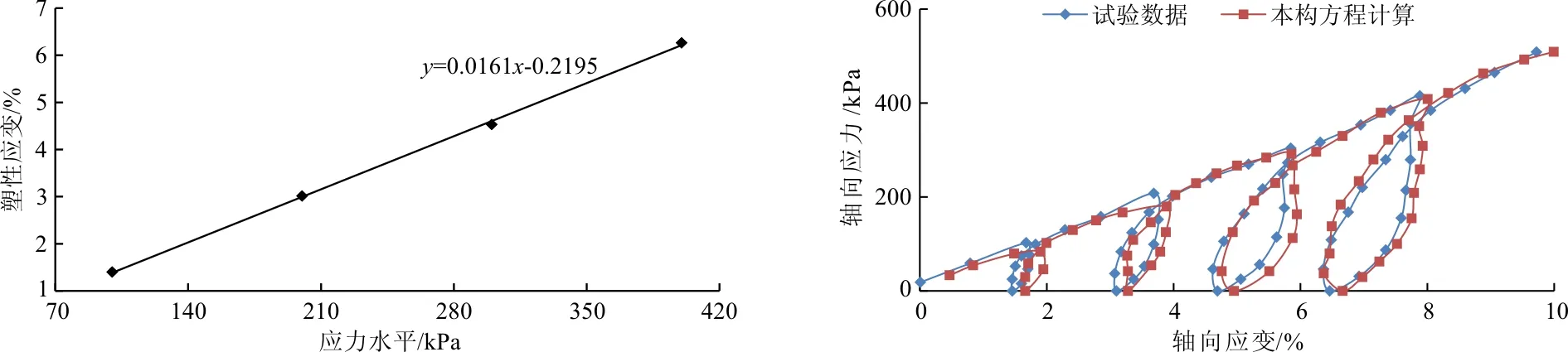
圖5軟土土樣塑性應變與卸載載荷關系 圖6本構方程計算結果與試驗數據對比

3.3 塑性滯回環分析

飽和軟土土樣循環加卸載試驗的塑性滯回環示意圖見圖7。從圖7可以看出，飽和軟土加卸載試驗再加載曲線與卸載曲線并不重合，而是形成一個封閉的滯回環，這是由于飽和軟土具有一定的塑性變形，且隨著荷載等級越高，滯回環的面積越大，表明飽和軟土的塑性越大[10]。用滯回環的面積表示飽和軟土在加卸載過程中滯回能的大小[3]，而滯回能是描述加卸載過程中能量消耗的重要參數，本文就滯回能的變化規律進行如下分析。

(24)

式中：Wi為每級卸載再加載過程中的滯回能；εpi為卸載為零時的應變；εui為卸載曲線與再加載曲線上交點所對應的應變；σli為滯回環上各級再加載曲線任意時刻的軸向應力；σui為滯回環上各級卸載曲線任意時刻的軸向應力。

將公式(20)、(22)代入公式(24)中計算滯回能如下：

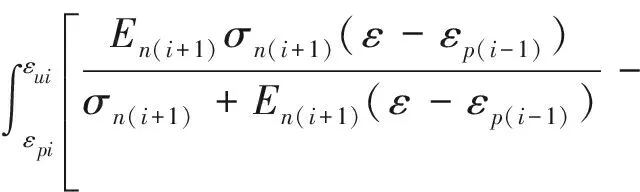
(25)

利用公式(25)計算滯回能見表3，并建立滯回能與卸載應力等級的關系。

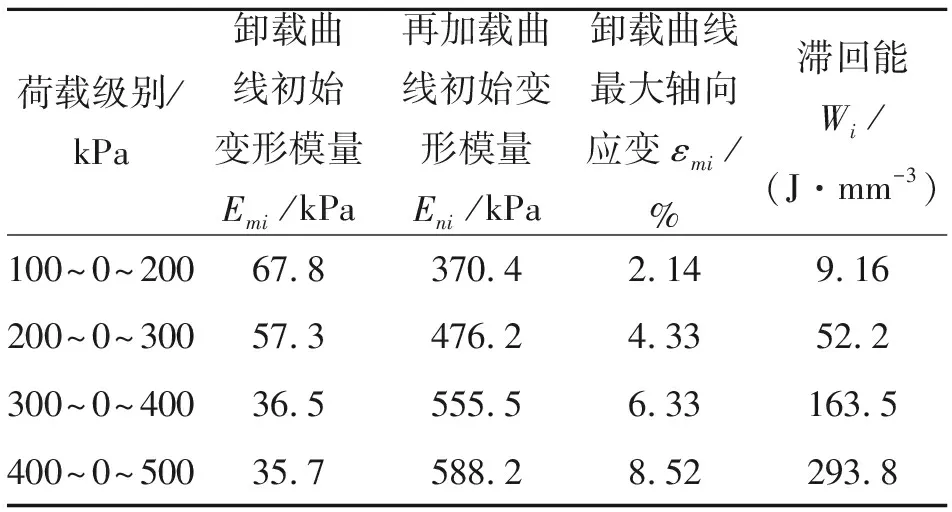
表3 各級卸載應力水平下的滯回能

試樣加載最大軸向應變εmax以及各級卸載為零時試樣的軸向應變εpi可根據圖7解出來，將表3中的參數代入公式(25)則可求出塑性滯回能的大小。從表3可以看出，隨著荷載等級的不斷增大，各級卸載曲線初始變形模量不斷減小，而再加載曲線的初始變形模量則不斷增大，各級滯回能也不斷增大，這是由于隨著試樣循環荷載的增大，土體的塑性在不斷增大。

本文對塑性滯回能與卸載應力水平的關系進行整理，得到了兩者呈二次曲線關系，如圖8示。

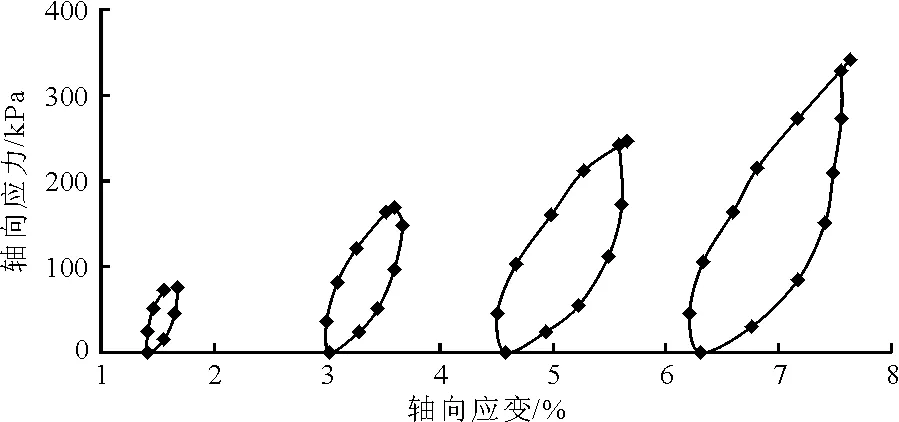
圖7 飽和軟土土樣加卸載試驗塑性滯回環示意圖

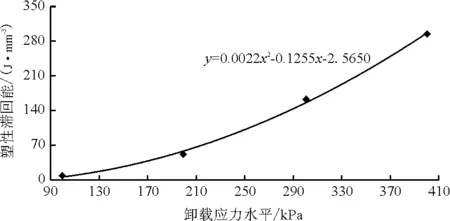
圖8 塑性滯回能與卸載應力水平的關系

根據圖8，可將塑性滯回能和卸載應力水平用下列回歸方程表示：

(26)

式中：Wi為塑性滯回能，J/mm3；σi為各級卸載應力水平,kPa；A,B,C為回歸系數。

4 結 論

本文通過對飽和軟土開展軸向循環加卸載試驗的數據進行分析，得出以下主要結論：

(1)各級卸載與再加載曲線的變化趨勢是相同的，試樣的變形表現出了非線性特性，卸載和再加載曲線主要有曲線段組成，當再加載曲線荷載超過上級卸載荷載時，曲線近似為一條直線，且沿著初始加載曲線上升。這些規律可通過對試驗過程中的變形模量分析來加以驗證；

(2)由于軟土試樣具有可塑性，所以在試驗過程中試樣的變形主要包括彈性變形和塑性變形兩個部分，通過試驗數據求得試驗彈性變形和塑性變形，并且分析后，可知彈性變形和塑性變形均與卸荷應力水平呈線性關系；

(3)通過利用加卸載曲線的初始變形模量推導出了卸載和再加載兩個過程的軸向應力與軸向應變的雙曲線本構方程，并驗證了其可靠性；

(4)通過對試驗曲線的分析計算，得到試樣加卸載過程中消耗的塑性滯回能與卸載應力水平呈良好的雙曲線關系，且隨著荷載等級增大而增大。