ST-CFSFDP：快速搜索密度峰值的時空聚類算法

王培曉,張恒才,王海波,吳 升

1. 福州大學數字中國研究院(福建)，福建 福州 350002； 2. 中國科學院地理科學與資源研究所資源與環境信息系統國家重點實驗室，北京 100101； 3. 海西政務大數據應用協同創新中心，福建 福州 350002； 4. 湖北工業大學經濟與管理學院，湖北 武漢 430068

近年來，室內外定位技術迅猛發展，如北斗、GPS、WiFi、藍牙、UWB(ultra-wideband)等，海量移動終端不斷普及，如PDA、智能手機、平板電腦等，網絡技術不斷進步，室內外位置服務應用不斷增多，如在線導航、基于位置的社交網絡、基于位置的廣告推送、商業物流調度與管理等，時空軌跡數據爆發式增長[1-2]，為人類出行模式及人類移動性、城市計算、社會計算、交通管理、城市規劃、人口流動監測、公共安全保障等研究提供了重要支撐[3-4]。

聚類算法是發現時空模式、探尋移動規律的關鍵技術之一，旨在將實體劃分為一系列具有一定分布模式的簇集，同一簇集中的實體具有較大的相似度，不同簇集中的實體具有較大差別[5-8]，已廣泛應用于犯罪熱點分析[9]、地震空間分布模式挖掘[10]、制圖自動綜合[11]、遙感影像處理[12]、公共設施選址[13]、地價評估[14]、用戶停留區域識別[15]等研究。

目前，聚類算法大致分為[6,16]：基于劃分、基于層次、基于密度、基于格網的聚類算法。基于劃分聚類算法使用聚類中心(位于簇集中心附近的一個對象)來表示每個簇集，如經典的k-means[17]算法和K-Medoid[18]算法，具有計算邏輯簡單、運算效率高等優點；基于層次聚類算法使用逐步合并或分裂的策略來實現聚類，如改進的CURE[19]算法，不僅能發現球形的空間簇集[20-21]，也能夠發現較為復雜結構的空間簇集，但過多的超參數增加了算法的不確定性；基于密度聚類算法，如DBSCAN[22]將簇定義為密度相連的點的最大集合，但由于采用固定閾值聚類，難以適應空間實體密度的變化[23]，OPTICS[22,24]算法為聚類分析生成一個增廣簇排序，解決了DBSCAN算法全局密度閾值的缺點；基于格網的聚類算法[25]其聚類效果依賴于網格的大小，如果網格劃分過細，則時間復雜度會顯著增加，如果網格劃分過粗，則聚類質量難以得到保證。

此外，許多研究學者在經典聚類算法基礎之上，提出了時空聚類算法，文獻[26—27]在基于密度聚類的基礎上提出了時空密度聚類ST-DBSCAN和ST-OPTICS算法，在時空密度聚類中，使用時間距離將空間鄰域擴展到時空鄰域，從而尋找時空鄰域下密度相連的區域。文獻[10,28]采用時空距離(時間距離與空間距離的函數)度量任意兩個時空事件的差異，后將時空距離應用到傳統的聚類算法中挖掘時空事件的模式；文獻[29—30]在空間掃描統計的基礎上提出了時空掃描統計算法，通過滑動掃描窗口(空間半徑和時間間隔定義的圓柱體)揭示時空事件隨時間聚類模式；文獻[31]通過窗口距離與時空最近鄰的概念重新定義了時空密度，從而提出了STSNN算法；文獻[32]從統計學的視角提出了WNN算法，將時空鄰域中的實體分為特征與噪聲兩個時空泊松點過程，使用密度相連(density-connective)的概念將特征分為多個簇集；文獻[33—34]分別在基于劃分和基于層次聚類基礎上提出了WKM和ST-AGNES算法，將其分別應用于人類行為和用戶停留區域識別中，并取得了較好的聚類效果。

經典的CFSFDP[35](clustering by fast search and find of density peaks)算法結合了基于劃分和基于密度聚類算法的優點，不僅可以發現多密度任意形狀的簇集，還可以通過決策圖輔助識別聚類中心的個數。但該算法無法很好地應用于時空數據聚類研究之中，究其原因在于CFSFDP算法未考慮時間約束，如圖1所示，并沒有正確識別簇集。如錯誤地將簇集A(t5,t6,t7,t8)、C(t15,t16,t17,t18)合并為一個簇集，且并不能發現簇集之間的順序關系。此外，在單簇集中存在多個密度峰值點時，該算法將會產生錯誤的時空聚類結果。

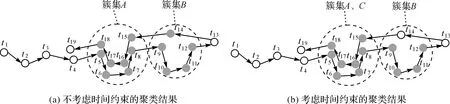
圖1 是否考慮時間約束的兩種聚類結果Fig.1 Comparison of clustering results with and without time constraints

鑒于此，本文提出一種快速搜索密度峰值的時空聚類算法(spatial-temporal clustering by fast search and find of density peaks，ST-CFSFDP)，在CFSFDP算法的基礎上引入了時間約束，修改了樣本屬性值的計算策略。采用模擬數據和真實數據案例進行算法有效性的驗證。模擬數據試驗結果表明，與CFSFDP算法相比，ST-CFSFDP算法不僅可以克服單簇集中可能存在多密度峰值的不足，且可以區分并識別相同位置不同時間的簇集。以移動對象軌跡中停留點識別為例，ST-CFSFDP算法較經典的ST-DBCSAN、ST-OPTICS和ST-AGNES算法識別正確率分別可提高5.2%、4.2%和7.6%。

1 ST-CFSFDP算法

1.1 CFSFDP算法

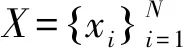
ρi=∑jχ(dij-dc)

(1)

(2)

式中，dij為樣本點i和樣本點j之間的空間距離；dc是人為指定的超參數，稱為截斷距離；χ(x)表示0～1函數，當x<0時，χ(x)=1,當x≥0時，χ(x)=0，即局部密度ρi表示落在以樣本點xi為圓心，截斷距離dc為半徑的圓形區域中樣本點個數；δi表示局部密度大于xi的所有樣本點中，距離xi最近的樣本點與xi之間的距離,由于式(2)無法計算密度最大的樣本點，因此密度最大的樣本點δi=max (dij)。

CFSFDP算法通過各樣本點的局部密度ρi和距離δi確定聚類中心(ρi和δi均相對較大的樣本點)。如圖2(a)所示，對于數據集X中每一個樣本點xi，計算其局部密度ρi和距離δi，生成相應的三元組(ρi,δi,λi)，λi表示δi對應的節點編號，用于非聚類中心樣本點的類別分配，使用ρi和δi構造數據集X的決策圖(decision graph)，如圖2(b)所示。容易發現，標號為①和⑩的樣本點同時具有較大的ρ值和δ值，因此被確定為數據集X的兩個聚類中心。為了更加方便地確定數據集X中的聚類中心，文獻[35]提出了一個綜合考慮ρ和δ的量γ。

γi=ρiδi

(3)

(4)

1.2 基于時空約束的ST-CFSFDP聚類算法

ST-CFSFDP算法首先在CFSFDP算法的基礎上引入了第2個超參數tc，針對時間序列數據集X，修改了ρ與δ的計算策略。其中時間約束下的局部密度ρ計算方法如式(5)所示

ρi=∑jχ(dij-dc,tij-tc)

(5)

(6)

式中，tqiqj表示樣本點xqi與樣本點xqj的時間距離，即修改后的δ根據樣本點的局部密度降序依次計算，即使單簇集中存在多個密度峰值，依舊僅有一個樣本點被選做聚類中心。然而當單簇集的時間跨度過長時，僅使用時間距離計算δ同樣會將單簇集分裂成多個小簇集。如圖4(b)所示，假設簇集C內部的樣本點4、k具有較高的局部密度ρ，由于兩樣本點的時間跨度較大，兩點都將具有較大的δ，依據本文的計算策略γi=ρiδi，簇集C將產生兩個聚類中心。為解決這個問題，本文添加了聚類中心合并的過程，將識別的聚類中心按時間順序鏈接，分別計算相鄰兩聚類中心的距離，若小于距離鄰域dc，將相鄰兩個聚類中心合并，經聚類中心合并后，聚類中心的個數將與簇集的個數一一對應。

在ST-CFSFDP算法中，剩余樣本點的分配沿時間軸進行。如圖5所示，針對時間順序分布的數據集X，首先識別數據集中的聚類中心(紅色樣本點為合并后的聚類中心)，然后每個聚類中心沿時間軸向前、后搜索本簇集中的剩余樣本點，以聚類中心CP2向前搜索為例，尋找CP2前一時刻的樣本點t15，計算樣本點與CP1和CP2的距離，如果距離CP2近，則將樣本點t15歸屬于CP2，否則聚類中心CP2向前搜索完畢，以同樣的策略向后搜索最終確定該簇集包含的所有樣本。所有聚類中心依次搜索完畢后，未被分配類別的樣本點為離群點，以圖5黃色樣本點為例，聚類中心CP2延時間軸向后搜索時，由于黃色樣本點OP1距離聚類中心CP3較近，因此聚類中心CP2向后搜索結束，當聚類中心CP3延時間軸向前搜索時，黃色樣本點OP2距離聚類中心CP2較近，因此聚類中心CP3向前搜索結束，此時黃色樣本點OP1與OP2之間的樣本點為離群點。ST-CFSFDP算法整體實現流程如下。

算法 快速搜索密度峰值的時空聚類算法

輸入：序列數據sequence=={ti,pi},距離閾值disthr,時間閾值tthr

輸出：每一個樣本點的聚類類別labels={ci}

functionST_CFSFDP (sequence, disthr,tthr)

∥計算樣本點的空間距離矩陣

stDisMat=computeSpatialDisMat(sequence)

∥計算樣本點的時間距離矩陣

timeDisMat=computeTimeDisMat(sequence)

∥計算樣本點在時空約束下的局部密度

densityArr=computeDensity(stDisMat,disthr,

timeDisMat,tthr)

∥獲得局部密度降序排列的下標序列

densitySortArr=argsort(densityArr)

∥初始化數組，用于存放每個軌跡點的屬性δ

closestDis=[]

fori=0→len(densitySortArr)do

∥獲得當前樣本點的索引

node=densitySortArr[i]

∥獲得比當前樣本點局部密度更大的索引集合

nodeIdArr=densitySortArr[i+1;]

∥計算每一個樣本點的屬性δ

closestDis[node]=compute(node, nodeIdArr,

stDisMat,timeDisMat)

endfor

∥計算每一個樣本點的屬性γ

gamma=closestDis*densityArr

∥通過決策圖得到聚類的數目

classNum=getNumFromDecisionGraph(gamma)

∥獲取樣本點的聚類類別

labels=extract_clustering(gamma,classNum,

stDisMat,timeDisMat)

returnlabels

endfunction

1.3 算法時間復雜度分析

ST-CFSFDP算法的時間復雜度定性描述了該算法的運行時間。ST-CFSFDP算法的時間復雜度主要由兩部分組成：計算樣本點的局部密度ρ和距離δ，其中ρ和δ的計算都涉及樣本點之間的距離計算。在數據集規模為n的情況下，①計算任意兩個樣本點之間的距離，時間復雜度為O(n2)；②計算n個樣本點的局部密度δ，時間復雜度為O(n2)；③計算n個樣本點的距離δ，時間復雜度同樣為O(n2)。因此，ST-CFSFDP算法的時間復雜度為O(n2)。

圖2 數據集X及其決策圖Fig.2 Dataset X and its decision graph

圖3 遞減順序排列的γFig.3 The value of γ in decreasing order

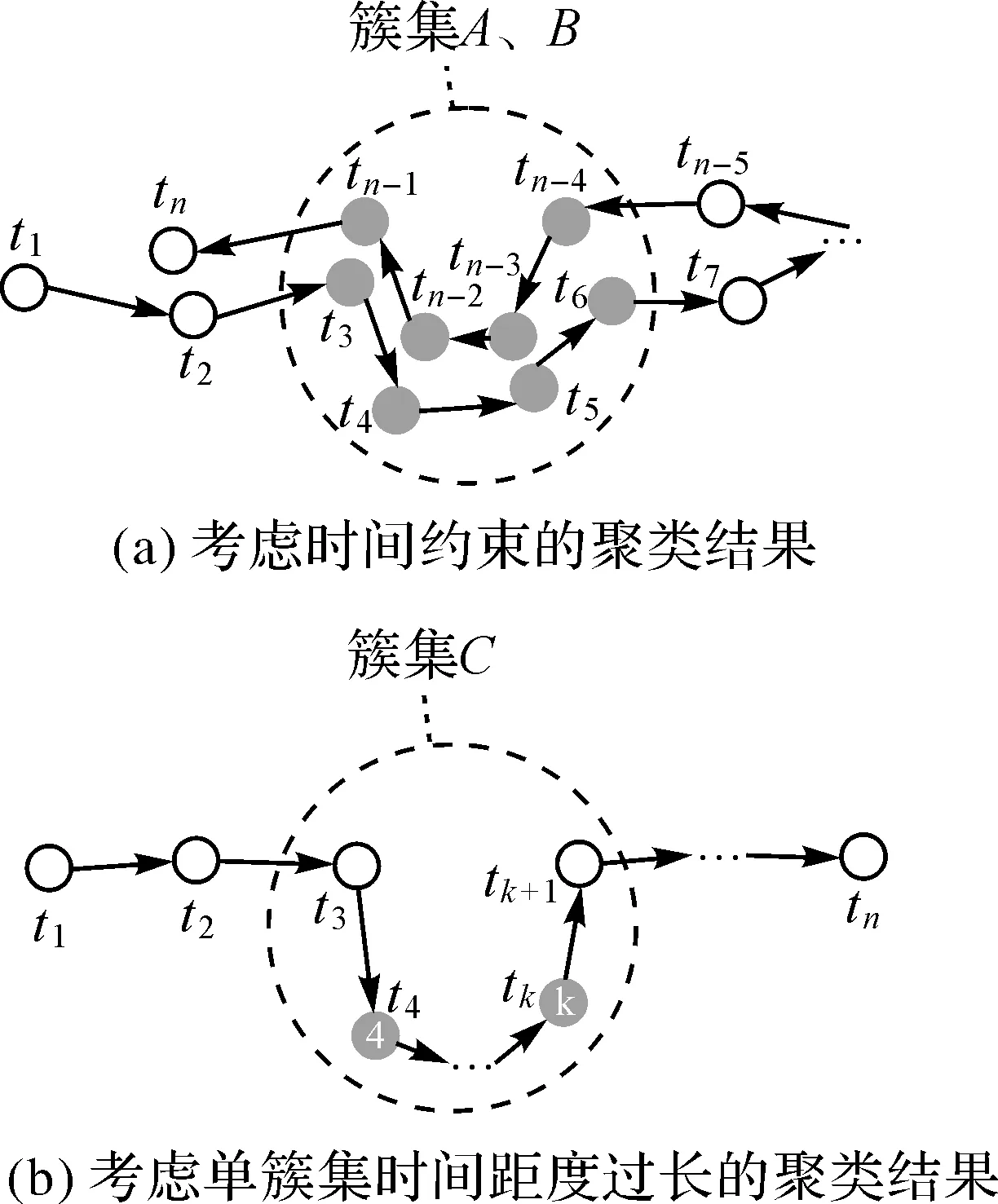
圖4 CFSFDP算法改進Fig.4 Improvement of CFSFDP algorithm

圖5 ST-CFSFDP算法剩余點分配Fig.5 Distribution of non-clustered center points of ST-CFSFDP algorithm

2 試驗結果與討論

2.1 試驗數據

為分析ST-CFSFDP算法的性能，分別采用模擬數據集和真實用戶軌跡進行試驗。采用模擬數據集進行試驗的主要目的是以二維圖形的方式直觀地展示聚類結果，采用真實用戶軌跡進行試驗的主要目的是使用相關指標定量地評價聚類算法的性能。

本文共模擬4組數據量不同的時序數據集X。每組模擬數據集的生成過程如下：首先生成指定的具有時間約束的幾何形狀，然后根據指定的幾何形狀等時間間隔采樣而成，其中一組數據如圖6(a)、(b)所示。

真實數據來源于濟南市某廣場移動用戶的WiFi定位數據。用戶移動定位數據是一種典型的時空數據，在一定程度反映了用戶的個人生活習慣和日常行為模式。時空聚類算法常用于從用戶移動定位數據識別用戶的停留區域，從而進一步挖掘用戶的興趣愛好，因此本文將ST-CFSFDP算法應用于停留區域識別并定量的評價該算法的性能。移動用戶定位數據覆蓋廣場5個樓層，平均采樣為1～10 s不等，定位精度約為3 m。由于定位數據難以獲取用戶停留區域的標注數據，因此本文采用爬蟲技術從百度地圖上獲取了該廣場的商鋪數據，借助商鋪數據標注用戶軌跡中的停留信息。標注過程如下：首先對商鋪數據與藍牙定位數據求交，然后統計某用戶在商鋪內部的持續停留時間，若用戶在商鋪內部的持續停留時間超過一定閾值，則將相應的軌跡點標注為停留點。依據上述規則，本文共標注472條用戶軌跡(當用戶軌跡中停留區域過少時，本文認為該軌跡價值不高，刪除該軌跡)，軌跡點總記錄量為935 639個。經標注后的某用戶軌跡數據如表1所示，每條記錄包括用戶唯一標識ID、記錄時間、用戶位置(X、Y坐標及所在樓層ID)、停留的商鋪ID(-1代表用戶未停留)。

圖6 模擬數據集Fig.6 Simulated data sets

表1 單用戶軌跡數據實例

2.2 算法評價指標及對比試驗選擇

本文以準確率(accuracy)和召回率(recall)作為停留區域識別的定量評價指標。用戶停留區域可理解為時間約束下用戶軌跡中的簇集，進一步可抽象為[36]S=(userID,Lng,Lat,arrT,levT)，(Lng,Lat)表示停留區域內的某個點坐標，其應最大概率出現在停留區域內部，一般為區域內所有軌跡點的均值坐標，本文為聚類中心坐標；arrT表示用戶抵達停留區域的時間；levT表示用戶離開停留區域的時間。停留區域識別結果是否正確主要依賴3個方面：①識別的停留區域和標注的停留區域數量是否一致；②識別的停留區域(Lng,Lat)坐標是否處于標注商鋪內部；③識別的停留區域起止時間(arrT,levT)是否與標注數據一致。結合上述3個方面，本文accuracy和recall計算方法如式(7)、式(8)所示。

(7)

(8)

式中，SClabel表示標注的停留區域個數；SCalgorithm表示算法識別的停留區域個數；SCcorrect表示算法判斷正確的停留區域個數，本文采用SO和TO[15]兩個函數共同判斷某個停留區域是否識別正確(SO函數判斷識別結果和標注數據在空間上是否鄰近，TO函數判斷識別結果和標注數據在時間上是否重合)。本文將ST-DBSCAN、ST-OPTICS、ST-AGNES、ST-CFSFDP時空聚類算法進行對比，探討4種時空聚類算法在不同閾值下準確率和召回率的變化情況。

2.3 模擬數據集上的測試結果分析

CFSFDP與ST-CFSFDP算法在模擬數據集上的聚類結果如圖7(e)、7(f)所示：①對于區域A，由于存在兩個聚類中心，使用CFSFDP算法，分裂成兩個小簇集，產生了錯誤的聚類結果，而使用ST-CFSFDP算法，依據改進的屬性計算策略，只聚類成一個簇集，從而得到更合理的聚類結果；②對于區域B，由于CFSFDP算法未考慮數據的時間約束，因此只聚類出一個簇集，而ST-CFSFDP算法考慮數據的時間約束，所以可以聚類出相同位置但不同時間的兩個簇集；③對于區域C，使用ST-CFSFDP算法識別出兩個聚類中心，但僅產生一個簇集，原因是其中一個小簇集時間跨度過長，在該簇集中識別出兩個聚類中心，但ST-CFSFDP算法最終會將這兩個聚類中心合并(相鄰聚類中心的距離小于距離閾值dc)，因此最終只產生一個簇集。綜上所述，與CFSFDP算法相比，ST-CFSFDP算法不僅克服了單簇集中可能存在多密度峰值的不足，且實現了考慮時間約束的時空聚類。ST-CFSFDP算法與ST-DBSCAN、ST-OPTICS、ST-AGNES算法的聚類結果如圖8所示，進一步說明ST-CFSFDP算法具有發現時空簇集的能力。

由上文分析可知，ST-CFSFDP算法具有良好的聚類性能，不僅解決了單簇集存在多密度峰值的問題，還能正確發現時空數據集的簇分布特征。進一步分析算法的運行時間，表2為兩種聚類算法在4組模擬數據集上運行時間的對比。試驗結果可以看出，ST-CFSFDP算法的時間開銷要略大于CFSFDP算法，這主要是因為ST-CFSFDP算法在計算樣本點局部密度時增加了時間開銷。但是這兩種算法的時間復雜度的均為O(n2)。與ST-DBSCAN、ST-OPTICS、ST-AGNES算法的運行時間相比，ST-CFSFDP的運行時間較小，能夠較快地得到聚類的運行結果。

表2 時空聚類算法運行時間在模擬數據集對比分析

Tab.2 The running time of spatio-temporal clustering on simulated data sets

數據集X記錄數CFSFDPST-CFSFDPST-DBSCANST-OPTICSST-AGNES3140.00450.00480.0052 0.03120.003334540.21590.29820.80581.97230.232463630.68390.84203.122110.6710.7918156234.00945.879115.627626.5154.8917

2.4 真實數據集上的測試結果分析

為評價ST-CFSFDP算法性能，本文參考室內房間寬度將初始距離閾值設置為1 m，并以0.5 m步長遞增；初始時間閾值設置為50 s，以20 s步長遞增；以啟發式的方法[22]設置ST-DBSCAN、ST-OPTICS算法中minPts參數，minPts=ln(N)，N為某用戶軌跡點數量。算法識別結果的準確率對比如圖9所示。4種算法的識別準確率變化趨勢在整體上較為相似，在時間閾值固定的情況下，準確率均隨著距離閾值的增加呈現先增加后下降的趨勢。綜合4種算法在不同閾值下的表現可以發現：①ST-CFSFDP算法對參數敏感度低，ST-DBSCAN與ST-OPTICS算法對參數敏感度較高(準確率隨著超參數的改變波動較大)；②相較ST-DBSCAN、ST-OPTICS、ST-AGNES算法，ST-CFSFDP算法準確率較高，在時間閾值90 s時最為明顯，ST-CFSFDP算法準確率最高可達82.4%，與現有算法相比，最高可提升7.6%；③ST-DBSCAN、ST-OPTICS算法本質上是一種算法，所以兩種算法的準確率高度一致；④ST-AGNES算法隱含時間約束，僅需要距離閾值即可完成聚類，因此算法準確率不受時間閾值的影響。

算法識別結果的召回率對比如圖10所示。4種算法的召回率均隨距離閾值增加呈現先增加后下降的趨勢，與算法準確率一致。當時間閾值為90 s時，4種算法的召回率較高，原因在于人工標注時用戶的停留時間閾值與90 s較接近。在此閾值下4種算法將會得到較精確的識別結果。與此同時ST-CFSFDP算法的召回率略高于其余3種算法且準確率與召回率波動最小，原因為ST-CFSFDP算法采用聚類中心作為用戶最可能的停留位置，而聚類中心作為局部范圍內密度最大的點，受閾值影響較小。本文將4種算法最高準確率相應的運行時間進行對比，結果如表3所示。ST-CFSFDP算法與ST-AGNES算法相比，ST-CFSFDP算法的運行時略高，但算法的識別正確率卻可提升7.6%；與ST-DBSCAN算法相比，ST-CFSFDP算法的運行時間略有降低且識別準確率提升了5.2%；與ST-OPTICS算法相比，ST-CFSFDP算法的運行時間得到了大幅度提升且識別準確率也有一定程度的提高。

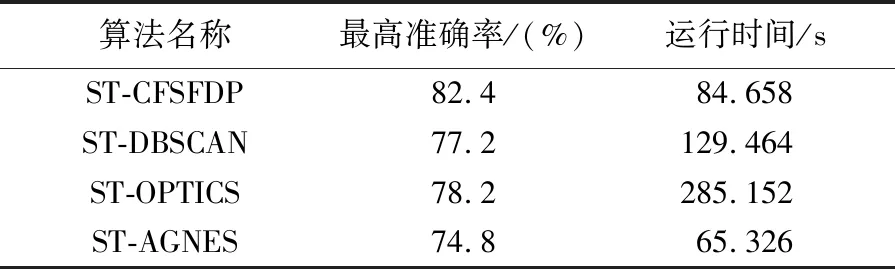
表3 4種算法運行時間對比分析

3 結論與展望

CFSFDP算法是一種新穎的空間聚類算法，通過計算樣本點的屬性值γ，能夠快速發現數據集中的密度峰值點。然而當數據集的某簇集存在多密度峰值點時，該算法易產生錯誤的聚類結果，且CFSFDP算法無法實現考慮時間約束的時空聚類。針對以上兩點不足，本文提出了時空聚類算法ST-CFSFDP。ST-CFSFDP算法在CFSFDP算法基礎上加入時間約束，并修改了樣本屬性值的計算策略。為驗證算法的有效性，首先采用模擬數據進行定性試驗。結果表明，與原有的CFSFDP算法相比，ST-CFSFDP算法不僅可以克服單簇集中可能存在多密度峰值的不足，且可以區分并識別相同位置不同時間的簇集。最后本文將ST-CFSFDP算法應用于用戶的停留區域識別，結果表明，ST-CFSFDP算法在時間閾值90 s、距離閾值5 m的識別正確率高達82.4%，較經典的ST-DBCSAN、ST-OPTICS和ST-AGNES算法分別提高了5.2%、4.2%和7.6%。

本文尚在以下方面存在不足，需在后續工作中進一步研究：受試驗數據采樣間隔的限制，現有算法僅采用秒級時間粒度的數據進行驗證,當定位數據的采樣間隔增大時，算法識別準確率及可靠性需要進一步探究。

致謝：感謝上海圖聚智能科技股份有限公司為本研究提供室內定位軌跡試驗數據!