激光捷聯(lián)慣導(dǎo)振動(dòng)耦合問(wèn)題的精細(xì)建模

姚志強(qiáng)，雷宏杰，宋漢文，張 懿

(1.航空工業(yè)西安飛行自動(dòng)控制研究所，西安 710100；2.同濟(jì)大學(xué) 航空航天與力學(xué)學(xué)院，上海 200092)

近年來(lái)，隨著工業(yè)上對(duì)精密儀器精度要求的不斷提高，角振動(dòng)問(wèn)題日益受到廣泛學(xué)者的關(guān)注[1-2]。典型的精密儀器——激光捷聯(lián)慣導(dǎo)中，激光陀螺的性能對(duì)慣性導(dǎo)航的精度具有重要影響。為了消除小角速度輸入下陀螺無(wú)輸出的閉鎖效應(yīng)，激光陀螺工作時(shí)，其抖動(dòng)輪在持續(xù)的抖動(dòng)中[3]，因此陀螺抖動(dòng)是IMU除了來(lái)自載體的振動(dòng)和沖擊之外，主要的振動(dòng)源。工作條件下，陀螺的抖動(dòng)會(huì)引起慣性測(cè)量單元(IMU)的角振動(dòng)，若該角振動(dòng)在其它陀螺的敏感軸方向分量為零，則陀螺抖動(dòng)引起的振動(dòng)相互解耦，那么理論上陀螺在IMU中的性能指標(biāo)可以達(dá)到單個(gè)陀螺測(cè)試的性能指標(biāo)；反之，若該角振動(dòng)在其它陀螺的敏感軸方向分量不為零，則表明振動(dòng)存在耦合，陀螺性能將下降。本文通過(guò)對(duì)IMU的振動(dòng)建模，提出了彈性橢球的概念，給出了IMU振動(dòng)解耦的設(shè)計(jì)約束。

IMU的減振研究主要為減振模式的分析[4]、減振系統(tǒng)的設(shè)計(jì)[5-7]及減震器特性分析[8-10]。盡管研究人員發(fā)現(xiàn)IMU的質(zhì)心與彈性中心的重合可以實(shí)現(xiàn)線振動(dòng)與角振動(dòng)的解耦，慣性主軸與彈性主軸重合可以實(shí)現(xiàn)角振動(dòng)相互間的解耦[11-13]，然而，尚缺乏這一結(jié)論的理論導(dǎo)出過(guò)程。

本文針對(duì)陀螺抖振引起的IMU振動(dòng)，借助歐拉方程和拉格朗日方程導(dǎo)出了六自由度振動(dòng)方程。為了更為直觀的描述使振動(dòng)方程解耦數(shù)學(xué)約束，本文定義了彈性橢球這一概念，并分析了彈性橢球與慣性橢球不同位置關(guān)系下IMU的振動(dòng)響應(yīng)特點(diǎn)。

1 IMU振動(dòng)建模

振動(dòng)方程的建立采取慣性坐標(biāo)系P-xyz作為參考，各坐標(biāo)軸方向平行于靜態(tài)時(shí)IMU的慣性主軸方向。通常，慣性測(cè)量單元橡膠隔振系統(tǒng)安裝有8個(gè)上下對(duì)稱布置的隔振器[14]，如圖1所示。由于IMU臺(tái)體的剛度遠(yuǎn)大于減振器剛度，建模中將其視為六自由度剛體。

圖1 IMU及其支撐系統(tǒng)示意圖Fig.1 Sketch map of the IMU and its support system

2 基于動(dòng)量矩定理的歐拉方程

設(shè)IMU繞點(diǎn)P轉(zhuǎn)動(dòng)，固連于剛體的P-x*y*z*作為連體坐標(biāo)系。系統(tǒng)靜止時(shí)，P-x*y*z*與P-xyz重合。動(dòng)量矩定理在該坐標(biāo)系下的投影式為[15]

(1)

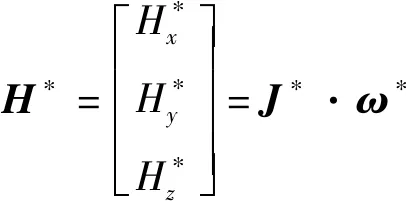
式(1)可改寫為

(2)

上式即為剛體定點(diǎn)轉(zhuǎn)動(dòng)歐拉運(yùn)動(dòng)方程。

2.1 基于拉格朗日方程的振動(dòng)方程

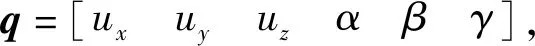
第i個(gè)支撐點(diǎn)(xi,yi,zi)處的位移變化量，即彈簧的變形量，由平動(dòng)和轉(zhuǎn)動(dòng)兩部分組成

(3)

CγCβCα為三次轉(zhuǎn)動(dòng)的方向余弦矩陣。設(shè)系統(tǒng)的角振動(dòng)可視為無(wú)限小轉(zhuǎn)動(dòng)，則方向余弦矩陣可簡(jiǎn)化為

(4)

將式(4)代入式(3)可得

(5)

由于實(shí)際的IMU設(shè)計(jì)通常采用三向等剛度減振器，若振動(dòng)中不考慮重力勢(shì)能的變化，僅考慮彈性勢(shì)能，則系統(tǒng)的勢(shì)能可表示為

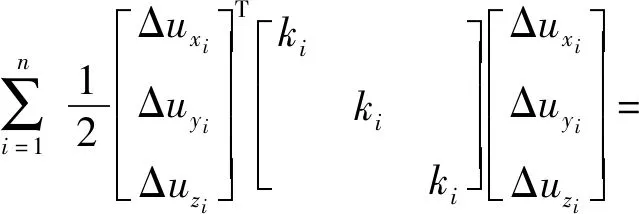
(ziβ)2+(xiγ)2+(yiα)2))+2(uxziβ+uyxiγ+uzyiα)-2(uxyiγ+uyziα+uzxiβ)-2(yiγziβ+ziαxiγ+xiβyiα))

(6)

若靜止?fàn)顟B(tài)下，系統(tǒng)質(zhì)心的位置坐標(biāo)為(xm,ym,zm)，則根據(jù)式可得dt時(shí)間微段內(nèi)，質(zhì)心的位移增量為

(7)

進(jìn)而質(zhì)心速度為

(8)

系統(tǒng)的動(dòng)能可表示為

(9)

根據(jù)式(9)和式(6)可以建立拉格朗日函數(shù)L=T-V，存在拉格朗日方程

j=1,2,3,4,5,6

(10)

將式(9)及式(6)代入式(10)，對(duì)于線振動(dòng)，即j=1,2,3，可得：

(11)

對(duì)于角振動(dòng)，需要考慮慣性坐標(biāo)系與主軸坐標(biāo)系之間的相互轉(zhuǎn)化。可將式(10)改寫為

j=4,5,6

(12)

(13)

(14)

將式(2)代入式(14)，將出現(xiàn)角度、角速度和角加速度的乘積項(xiàng)，通常該乘積項(xiàng)不可忽略。然而，在捷聯(lián)慣導(dǎo)系統(tǒng)中，激光陀螺機(jī)械抖動(dòng)機(jī)構(gòu)的抖動(dòng)頻率一般在100～400 Hz[16]，國(guó)內(nèi)相關(guān)研究院所生產(chǎn)使用的高頻激光陀螺的抖動(dòng)頻率也小于1 000 Hz。因此，慣導(dǎo)系統(tǒng)的角振動(dòng)頻率不會(huì)超過(guò)1 000 Hz。由于角速度和角加速度與角度滿足導(dǎo)數(shù)關(guān)系，對(duì)于無(wú)限小轉(zhuǎn)動(dòng)，因此可以認(rèn)為角速度和角加速度都為無(wú)限小量，無(wú)限小量的乘積項(xiàng)可視為高階無(wú)窮小略去。因此，上式可線性化為

(15)

此外，我們有：

(16)

結(jié)合式(12)、式(15)及式(16)可得

(17)

(18)

由式(17)、式(18)及式(11)可得系統(tǒng)的振動(dòng)方程

(19)

其中質(zhì)量矩陣為

M=

(20)

剛度矩陣為

K=

(21)

廣義力為

(22)

需要特別指出的是，上述結(jié)果的導(dǎo)出是建立在以下兩點(diǎn)簡(jiǎn)化之上的：① IMU作無(wú)限小轉(zhuǎn)動(dòng)，方向余弦矩陣式(4)忽略了二階小量；② 式(17)的導(dǎo)出忽略了IMU三個(gè)角振動(dòng)的二次交叉耦合項(xiàng)。

2.2 振動(dòng)方程的簡(jiǎn)化

本文只考慮陀螺抖動(dòng)引起IMU的振動(dòng)，從式(20)和式(21)可以看出，當(dāng)

xm=0,ym=0,zm=0

(23)

(24)

此時(shí)，角振動(dòng)方程可以獨(dú)立寫作

(25)

3 彈性橢球

注意到剛度矩陣式(25)中剛度矩陣各個(gè)元素的表達(dá)式，與質(zhì)點(diǎn)系慣性張量的矩陣表達(dá)式極為相似，該矩陣定義為

(26)

本文定義S為彈性張量的矩陣表達(dá)式。其對(duì)角元稱為彈性矩，非對(duì)角元稱為彈性積。質(zhì)點(diǎn)系慣性張量與彈性張量矩陣表達(dá)式唯一不同的是質(zhì)量被彈簧剛度所替換。因此，與慣性張量類似，在空間中應(yīng)該存在一個(gè)彈性橢球滿足方程

Sxxx2+Syyy2+Szzy2-2Sxyxy-

2Sxzxz-2Syzyz=k2

(27)

從解析幾何知道，一個(gè)橢球在空間中必然存在三根正交的主軸。如果我們把這三個(gè)主軸取作坐標(biāo)軸，彈性中心作為坐標(biāo)原點(diǎn)，那么彈性橢球的方程將簡(jiǎn)化為

Sxx2+Syy2+Szy2=k2

(28)

彈性橢球的主軸稱為彈簧對(duì)于彈性中心的彈性主軸，相應(yīng)的彈性矩Sx,Sy,Sz稱為主彈性。那么，當(dāng)坐標(biāo)軸方向進(jìn)一步與彈性主軸平行時(shí)，角振動(dòng)方程退化為

(29)

綜上所述，要使得IMU六個(gè)自由度上的振動(dòng)完全解耦，需要滿足以下兩個(gè)條件：① IMU的質(zhì)心與彈性中心重合(線振動(dòng)與角振動(dòng)解耦);② IMU的慣性主軸與彈性主軸重合(角振動(dòng)間相互解耦)。

工程實(shí)際中，可以通過(guò)合理布局減振器相對(duì)系統(tǒng)質(zhì)心的坐標(biāo)位置，實(shí)現(xiàn)質(zhì)心與彈性中心重合且慣性主軸與彈性主軸重合。

4 仿真驗(yàn)證

上述理論推導(dǎo)中，均未考慮彈簧阻尼的影響，假設(shè)阻尼矩陣與剛度矩陣形式相同。某型號(hào)減震器的通過(guò)設(shè)計(jì)參數(shù)計(jì)算出的彈簧剛度和阻尼分別為

k=84 739(N/m),c=53.68(N·s/m)

(30)

由于IMU被視為剛體，IMU內(nèi)部的結(jié)構(gòu)阻尼予以忽略，系統(tǒng)的阻尼完全由減震器提供，因此只需將式(21)中的彈性系數(shù)改為阻尼系數(shù)即可得到系統(tǒng)的阻尼矩陣。本文只考慮抖振的影響，三只陀螺的抖振頻率依次為550 Hz、606 Hz、714 Hz，以引起IMU產(chǎn)生單位靜扭轉(zhuǎn)的力矩為幅值，抖動(dòng)頻率為激勵(lì)頻率模擬激勵(lì)信號(hào)。

某型號(hào)IMU的幾何尺寸為90 mm×138 mm×129 mm，以質(zhì)心為坐標(biāo)原點(diǎn)，靜止?fàn)顟B(tài)下慣性主軸為坐標(biāo)軸，支撐系統(tǒng)如圖1所示。仿真算例中，計(jì)算了圖2所示的四種設(shè)計(jì)狀態(tài)下IMU的振動(dòng)響應(yīng)。圖2(a)為質(zhì)心與彈性中心重合，慣性主軸與剛度主軸平行;圖2(b)為質(zhì)心與彈性中心重合，慣性主軸與剛度主軸不平行；圖2(c)為質(zhì)心與彈性中心不重合，慣性主軸與剛度主軸平行；圖2(d)為質(zhì)心與彈性中心不重合，慣性主軸與剛度主軸不平行。圖中長(zhǎng)方體表示IMU，淺灰色橢球表示慣性橢球，深灰色橢球表示彈性橢球。

不同設(shè)計(jì)狀態(tài)下的繞Z軸角振動(dòng)及線振動(dòng)對(duì)比如圖3～圖5所示。

(a)雙心重合雙軸不重合Z軸角振動(dòng)

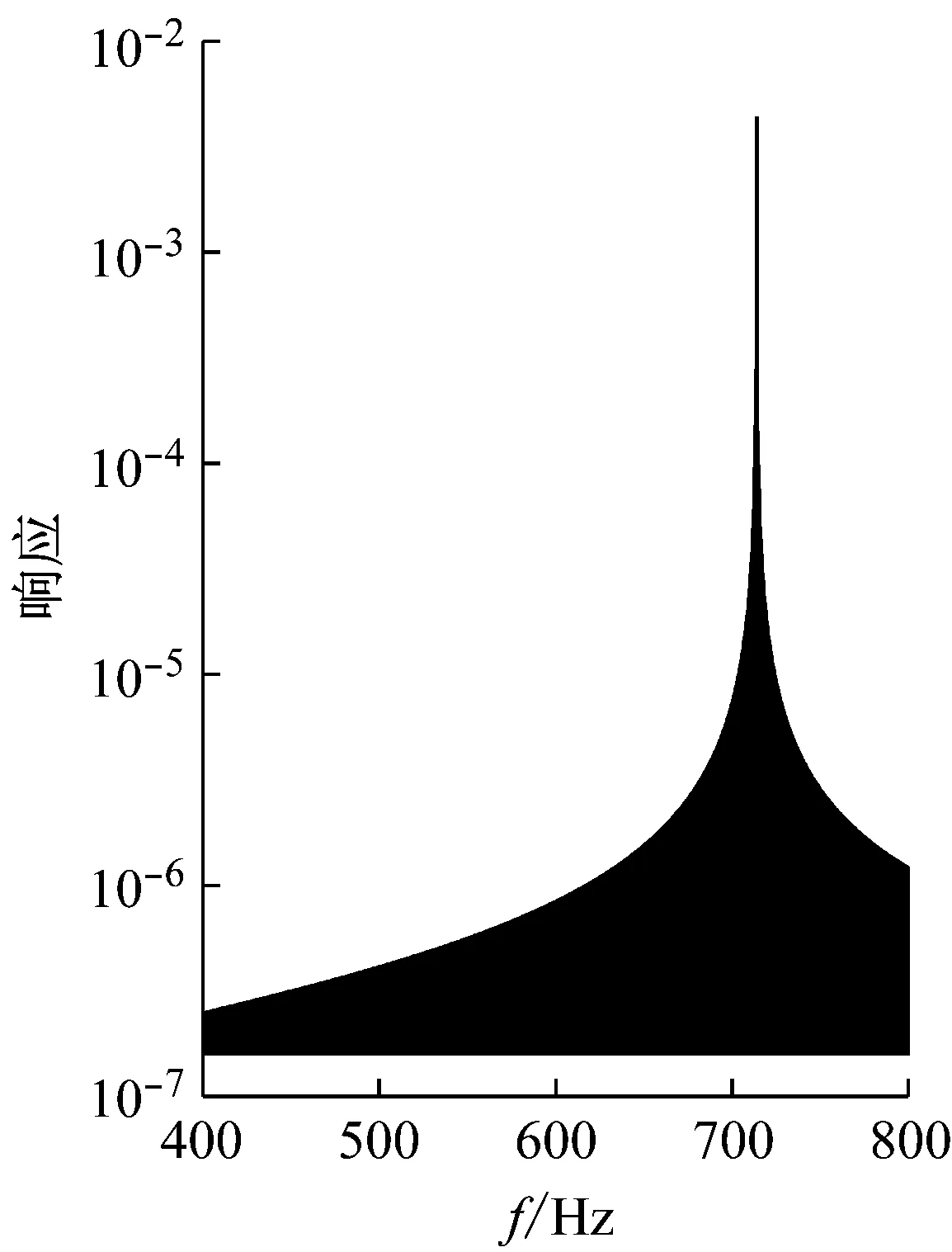
(b)理想設(shè)計(jì)Z軸角振動(dòng)圖3 雙心重合雙軸不重合與理想設(shè)計(jì)IMU對(duì)比Fig.3 The comparison between the idealized IMU with the IMU in which the two centers coincide and the two axis mismatch

(a)沿Z軸線振動(dòng)

(b)繞Z軸角振動(dòng)圖4 雙心不重合雙軸平行IMU響應(yīng)Fig.4 The response of the IMU in which the two centers mismatch and the two axis parallel

(a)沿z軸線振動(dòng)

(b)繞z軸角振動(dòng)圖5 雙心不重合雙軸不平行IMU響應(yīng)Fig.5 The response of the IMU in which the two centers mismatch and the two axis do not parallel

為了進(jìn)一步整體對(duì)比不同設(shè)計(jì)情形下IMU的響應(yīng)特點(diǎn)，本文將以上四種情形在陀螺工作頻率下的振動(dòng)響應(yīng)峰值繪制成柱狀圖，如圖6所示。

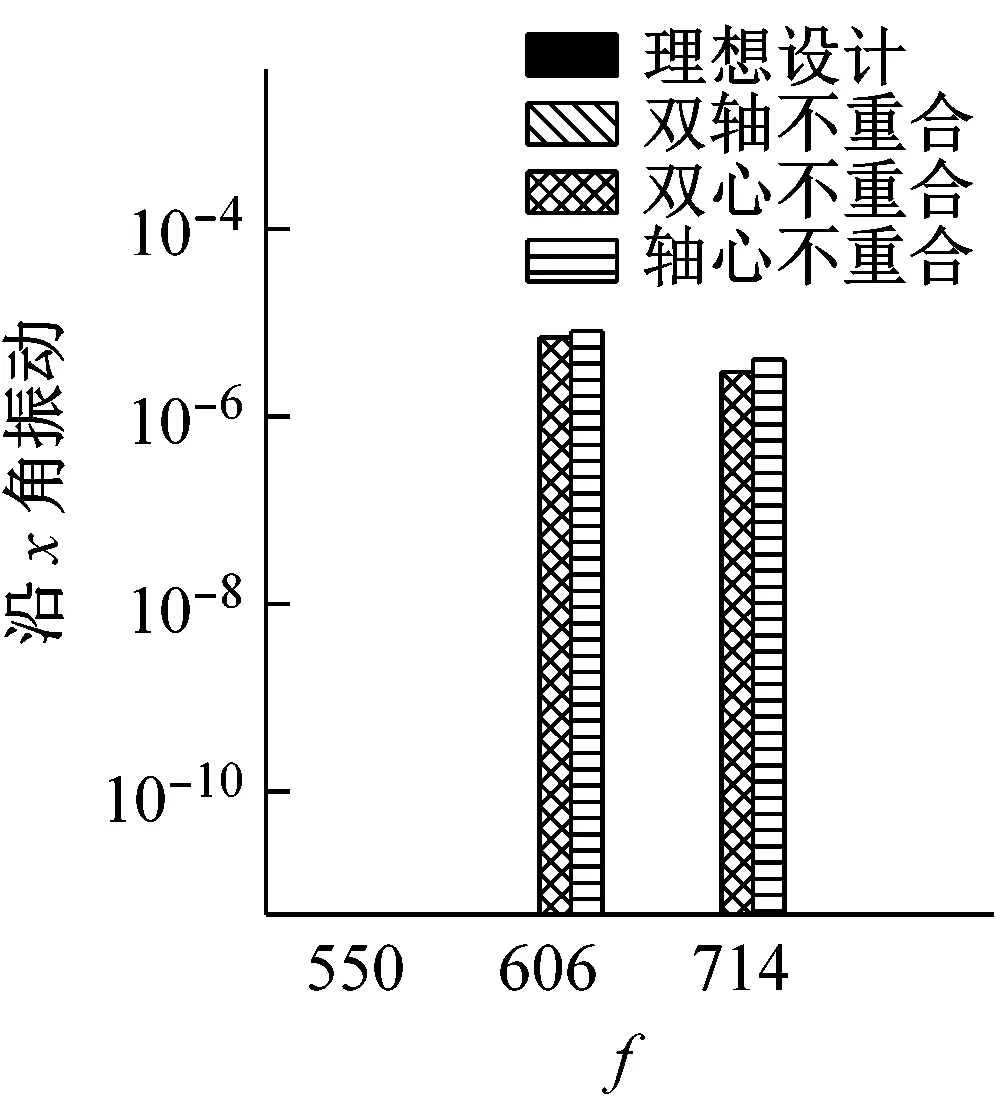
圖6 不同設(shè)計(jì)狀態(tài)下IMU響應(yīng)峰值對(duì)比Fig.6 The peak values of the response of the IMU under different designs

分析圖6可得到以下結(jié)論：

(1)雙心重合且雙軸重合時(shí)，三只陀螺的抖動(dòng)引起的IMU角振動(dòng)相互獨(dú)立，且不會(huì)引起IMU線振動(dòng)。

(2)雙心重合可以避免陀螺抖動(dòng)引起的耦合線振動(dòng)。

(3)系統(tǒng)偏心和雙軸不重合都會(huì)引起IMU不同程度的耦合角振動(dòng)和耦合線振動(dòng)。

5 結(jié) 論

激光捷聯(lián)慣導(dǎo)工作狀態(tài)下，為了消除閉鎖效應(yīng)，激光陀螺需要保持持續(xù)的抖動(dòng)，該抖動(dòng)是IMU的主要振動(dòng)源。工程實(shí)踐中，三只激光陀螺在IMU中逐個(gè)單獨(dú)工作的精度遠(yuǎn)高于同時(shí)工作的精度，進(jìn)一步的分析表明同時(shí)工作時(shí)陀螺間的耦合振動(dòng)是造成精度下降的主要原因。本文旨在提出陀螺振動(dòng)解耦的理論約束。

為了實(shí)現(xiàn)IMU的振動(dòng)解耦，本文從動(dòng)量矩定理和拉格朗日方程出發(fā)建立了任意設(shè)計(jì)狀態(tài)下IMU的振動(dòng)方程。對(duì)振動(dòng)方程的深入分析表明：若質(zhì)心與彈性中心重合，振動(dòng)方程將簡(jiǎn)化為線振動(dòng)與角振動(dòng)解耦的形式；在此基礎(chǔ)上，若慣性主軸與彈性主軸重合，振動(dòng)方程將在六個(gè)自由度上完全解耦。為了直觀描述這一結(jié)論，本文定義了彈性張量和彈性橢球。通過(guò)仿真計(jì)算了IMU不同設(shè)計(jì)狀態(tài)下，具體表現(xiàn)為彈性橢球和慣性橢球不同位置關(guān)系下，IMU的振動(dòng)響應(yīng)，驗(yàn)證了本文導(dǎo)出的振動(dòng)解耦理論約束。