發(fā)動機空氣彈簧液壓懸置動態(tài)特性及參數(shù)靈敏度研究

侯鎖軍，楊 慰

(1.河南工學院 車輛與交通工程學院，河南 新鄉(xiāng) 453000；2.中國汽車技術研究中心有限公司，天津 300300；3.東風商用車技術中心，武漢 430056)

隨著消費者對汽車乘坐舒適性要求的提高以及汽車市場產品競爭日益激烈，良好的汽車NVH特性正逐漸成為汽車產品競爭力的核心之一。然而汽車發(fā)動機大功率化和輕量化使得動力總成的振動激勵不斷加劇，這就對動力總成懸置系統(tǒng)的隔振特性提出了更高的要求，并希望其能滿足車輛使用過程中任何工況的需要[1-3]。

發(fā)動機懸置作為發(fā)動機的隔振元件，經(jīng)歷了橡膠懸置、被動式液壓懸置和半主動/主動液壓懸置的發(fā)展歷程[4-5]。橡膠懸置和被動式液壓懸置結構確定以后表征其動態(tài)特性的兩個參數(shù)動剛度和阻尼角是不可調的[6-9]，不能滿足汽車復雜工況對懸置動特性的要求。主動液壓懸置由于其結構和控制策略復雜，應用較少。半主動懸置結構和控制策略簡單，成本低，應用前景良好。其中空氣彈簧式半主動液壓懸置(以下簡稱空氣彈簧液壓懸置)是一種新型的、隔振性能良好的發(fā)動機隔振元件，其利用電磁閥控制懸置內部空氣腔的開閉改變懸置的動剛度和阻尼角，相對于其他類型半主動液壓懸置其動剛度和阻尼角變化范圍大，滿足了汽車發(fā)動機在不同工況下的對懸置隔振的要求。

Azadi等[10]設計了一種剛度可變的半主動懸置，通過調節(jié)壓電作動器和開關型控制器來改變可變剛度彈簧的預應剛度，使半主動控制懸置產生極大的動剛度特性，并且能耗很低。國內研究方面，賀良勇[11]對空氣彈簧液壓懸置進行了動特性分析研究。范讓林等[12]對解耦膜剛度可變的空氣彈簧液壓懸置進行了動特性分析研究。

通過分析空氣彈簧液壓懸置國內外研究現(xiàn)狀可見，對新型的發(fā)動機空氣彈簧液壓懸置的動特性研究還不夠深入，且較少有人對空氣彈簧液壓懸置動特性的影響因素進行靈敏度分析。本文設計了一款新型的空氣彈簧液壓懸置，其主要特點是在其他類型半主動液壓懸置的基礎上，加入了空氣彈簧結構。采用了上液室等效體積剛度替代解耦膜以及密閉空氣腔對懸置動特性的影響，基于流體力學相關理論建立了空氣彈簧液壓懸置力學模型，并通過試驗驗證了該模型的正確性，分析了空氣腔開啟和關閉時空氣彈簧的動態(tài)特性；采用該模型研究了空氣彈簧液壓懸置模型參數(shù)對懸置動剛度的影響，獲得了這些參數(shù)對空氣彈簧液壓懸置動剛度影響的靈敏度。

1 空氣彈簧液壓懸置結構與工作原理

1.1 空氣彈簧液壓懸置結構

本文所設計的空氣彈簧液壓懸置結構示意圖如圖1所示，主要包括：橡膠主簧、上液室、下液室、電磁閥、隔板、慣性通道、解耦膜、空氣腔、橡膠底膜。

1-連接動力總成的螺栓孔；2-連接車架的螺栓孔；3-金屬外殼；4-橡膠底膜；5-下液室；6-電磁閥；7-空氣腔；8-解耦膜；9-慣性通道；10-隔板；11-上液室；12-橡膠主簧
圖1 空氣彈簧液壓懸置的結構示意圖
Fig.1 Schematic diagram of air spring hydraulic mount

其中空氣腔是由解耦膜與隔板凹槽合圍形成的腔體，該空氣腔體通過一個小孔與外界大氣相通，但當電磁閥通電堵住小孔口時，則是密閉的空氣腔體，形成類似空氣彈簧。

1.2 空氣彈簧液壓懸置工作原理

空氣彈簧式液壓懸置工作時，上螺栓受動力總成激勵產生振動，帶動橡膠主簧對上液室作類似活塞泵吸的運動，于是上液室的體積連續(xù)地發(fā)生增大和縮小的變化，液體通過慣性通道在上下液室間來回流動，以適應上液室體積的變化。由于慣性通道壁和流動液體間的相互黏滯阻性，液體連續(xù)快速地通過時受到慣性通道的阻力，用來吸收來自動力總成的振動能量。空氣腔關閉時，自身剛度大，對橡膠主簧的作用力大，表現(xiàn)為懸置的動剛度大，空氣腔與大氣相通時，自身剛度較小，對橡膠主簧的作用力小，表現(xiàn)為懸置的動剛度小。

2 空氣彈簧液壓懸置建模

對解耦膜、空氣腔以及橡膠主簧的體積剛度進行的等效合并，在建立懸置模型時，不再單獨考慮解耦膜和空氣腔結構，而是以一個通過理論和試驗得出的等效上液室體積剛度來代替[13]。為突出影響懸置模型的主要因素，對半主動液壓懸置進行如下假設[14-15]：假設空氣腔內氣壓均勻，上、下液室內壓力均勻；忽略空氣腔內氣體溫度變化對氣壓造成的影響；上、下液室的體積剛度視為常量；液體為不可壓縮流體。液壓懸置的力學模型如圖2所示。

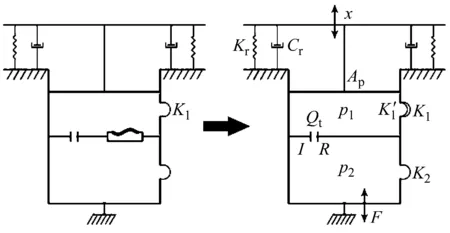
Ap-橡膠主簧泵吸液體的等效活塞面積;Kr、Cr-橡膠主簧的動剛度和阻尼系數(shù)；K1、K2-上液室和下液室的體積剛度；p1、p2-上液室和下液室的壓力；Qt-慣性通道內的液體流量；I、R-慣性通道內液體的慣性系數(shù)和流量阻尼系數(shù)；x、F-主簧振動位移和懸置的傳遞力
圖2 解耦膜與空氣腔等效合并后的懸置模型示意圖
Fig.2 Schematic diagram of the mount model after the equivalent combination of the decoupling membrane and the air chamber

由于解耦膜與橡膠主簧的體積剛度被等效合并，對于上液室的液體，可以建立液體流動的連續(xù)性方程[16-17]

(1)

與傳統(tǒng)的解耦膜式液壓懸置不同，本文設計的空氣彈簧液壓懸置的下液室液體并不與解耦膜/解耦盤下表面接觸，因此對于下液室的液體，可建立液體流動的連續(xù)性方程

(2)

對于慣性通道內的液體，液壓差與其受到的慣性力與阻尼力平衡，可以建立該部分液體流動的連續(xù)性方程

(3)

取整個系統(tǒng)作為研究對象，傳遞到車架固定端的力由橡膠主簧彈性力、阻尼力和上液室液壓力組成，即：

(4)

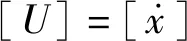
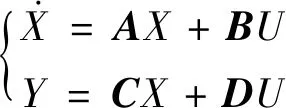
(5)

式中，U為輸入量，A為系數(shù)矩陣，B為控制系數(shù)矩陣，C為輸出狀態(tài)系數(shù)矩陣，D為控制系數(shù)矩陣，且有

將狀態(tài)方程和輸出方程寫成矩陣形式即為

(6)

y=F=

(7)

系統(tǒng)的傳遞函數(shù)為

(8)

其中s=jω，因此懸置的復剛度可表示為

(9)

式中，ω為角頻率，它可通過ω=2πf轉換為頻率。

對復剛度矩陣形式進行轉換和簡化，可以得到其表達式為

(10)

按照美國汽車工程學會修訂的《Testing Dynamic Properties of Elastomeric Isolators》中的定義，懸置的存儲剛度為復剛度的實部，阻尼角為復剛度虛部與實況比值的反正切值，即：

Kd=real(K*)

(11)

(12)

3 空氣彈簧液壓懸置動特性研究

試驗設備為美國的MTS831試驗臺，如圖3所示。試驗時，由試驗臺控制計算機的信號發(fā)生器產生所設定頻率和振幅的正弦信號，經(jīng)放大后加到作動器上，作動器下端固定，上端作動，上端的位移傳感器和力傳感器將信號傳遞給試驗臺的測試軟件，有測試軟件計算出懸置的動剛度和阻尼角的頻變特性曲線，其原理如圖4所示。測試樣件的內部結構如圖5所示。本文主要研究懸置的低頻垂向振動控制，測試Z向如圖6所示，作動器激勵頻率為0～50 Hz，懸置施加1 000 N的預載，振幅為1 mm。試驗過程中重復三次，取平均值。

圖3 試驗設備Fig.3 Test equipment

圖4 測試原理Fig.4 Test principle

該空氣彈簧懸置各個參數(shù)值如表1所示，將參數(shù)代入式(10)、(11)、(12)進行理論仿真，對該空氣彈簧液壓懸置的動剛度和阻尼角進行臺架試驗后，將空氣彈簧液壓懸置的動剛度和阻尼角仿真值與試驗值進行對比，結果如圖7～圖10所示。

1-動力總成端連接螺栓孔；2-橡膠主簧；3-金屬外殼；4-解耦盤總成；5-電磁閥；6-橡膠底膜
圖5 空氣彈簧液壓懸置結構
Fig.5 Structure of air spring hydraulic mount

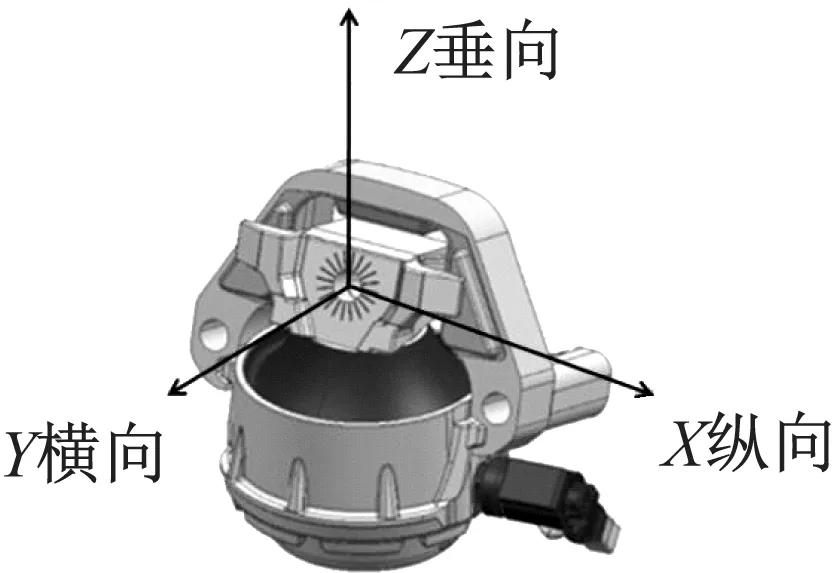
圖6 懸置三向示意圖Fig.6 Mount three-way diagram

表1 模型仿真參數(shù)
Tab.1 Model simulation parameters

參數(shù)數(shù)值橡膠主簧動剛度/(N·m-1)1.8×105橡膠主簧阻尼系數(shù)/(N·s·m-1)1.0×102橡膠主簧的等效活塞面積/m22.7×10-3空氣腔閉上液室等效體積剛度/(N·m-5)2×1010下液室體積剛度/(N·m-5)5×108慣性通道液體的質量慣性系數(shù)/(kg·m-4)2.5×106慣性通道液體的流量阻尼系數(shù)/(N·s·m-5)1.0×108

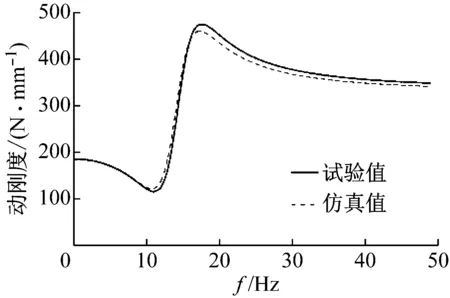
圖7 空氣腔關閉懸置動剛度對比Fig.7 Comparison of mount dynamic stiffness with the closed air chamber

有對比曲線可以看出，動剛度和阻尼角理論仿真與試驗曲線趨勢基本一致，在空氣腔關閉時，空氣彈簧懸置表現(xiàn)出大剛度大阻尼特性，動剛度達到最大值480 N/mm，阻尼角最大值62°，當空氣腔開啟時，空氣彈簧懸置表現(xiàn)出小剛度小阻尼特性，動剛度最大值僅有300 N/mm，阻尼角最大值僅有30°。比較空氣腔開啟和空氣腔關閉兩種狀態(tài)，動剛度增大了60%，阻尼角增大了106%，可以有效的進行發(fā)動機各種工況下的振動控制。

圖8 空氣腔關閉懸置阻尼角對比Fig.8 Comparison of mount damping angle with the closed air chamber

圖9 空氣腔開啟懸置動剛度對比Fig.9 Comparison of mount dynamic stiffness with the opened air chamber

圖10 空氣腔開啟懸置阻尼角對比Fig.10 Comparison of mount damping angle with the opened air chamber

4 模型參數(shù)靈敏度分析

在車型開發(fā)過程中，當發(fā)動機的型號及安裝位置確定后，需要對懸置的動剛度和阻尼角具體數(shù)值進行優(yōu)化才能達到發(fā)動機最佳的隔震性能，然后根據(jù)優(yōu)化設計后的懸置動剛度和阻尼角調整懸置內部結構參數(shù)，從而達到該優(yōu)化值。本文建立的懸置動力學仿真模型可較準確地表達空氣彈簧液壓懸置的動剛度和阻尼角，對懸置模型各參數(shù)進行調整達到其對動剛度和阻尼角的影響程度，為達到優(yōu)化后的懸置動剛度和阻尼角奠定了基礎。

本文在空氣彈簧液壓懸置各參數(shù)(如表1所示)基礎上浮動±50%，研究動剛度和阻尼角的變化規(guī)律及變化百分比。

4.1 橡膠主簧動剛度和阻尼對懸置動特性的影響

橡膠主簧的動剛度對懸置的動剛度的影響非常直接，如圖11、12所示，主簧動剛度在[0.9，2.7]×105N/m的范圍內線性上升時，懸置的動剛度也整體隨之線性上升，并且?guī)缀醪挥绊懛逯殿l率。懸置的阻尼角峰值隨著橡膠主簧動剛度的增大而減小，峰值頻率幾乎不受影響。

圖11 橡膠主簧動剛度對液壓懸置動剛度影響Fig.11 Influence of dynamic stiffness of rubber main spring on dynamic stiffness of hydraulic mount

圖12 橡膠主簧動剛度對液壓懸置阻尼角影響Fig.12 Influence of dynamic stiffness of rubber main spring on damping angle of hydraulic mount

橡膠主簧的阻尼系數(shù)在[0.5，1.5]×102N·s/m范圍內的改變對懸置動剛度和阻尼角峰值和峰值頻率都幾乎沒有影響，如圖13、14所示。

圖13 橡膠主簧阻尼系數(shù)對液壓懸置動剛度影響Fig.13 Influence of damping coefficient of rubber main spring on dynamic stiffness of hydraulic mount

4.2 橡膠主簧等效活塞面積對懸置動特性的影響

橡膠主簧等效活塞面積變化范圍為[1.35，4.05]×10-3m2，如圖15、16所示。隨著等效活塞面積的增大，懸置的峰值動剛度和大于18 Hz以后的動剛度大幅度地增大，但對頻率小于18 Hz時懸置動剛度影響不大，對懸置峰值頻率幾乎沒影響。橡膠主簧等效活塞面積對液壓懸置阻尼角的影響主要表現(xiàn)在頻率小于12 Hz處，隨著活塞面積的增大，阻尼角峰值增大，對懸置阻尼角峰值頻率影響較小。

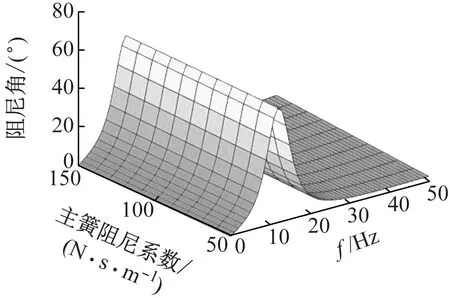
圖14 橡膠主簧阻尼系數(shù)對液壓懸置阻尼角影響Fig.14 Influence of damping coefficient of rubber main spring on damping angle of hydraulic mount

圖15 橡膠主簧等效活塞面積對液壓懸置動剛度影響Fig.15 Influence of equivalent piston area of rubber main spring on dynamic stiffness of hydraulic mount

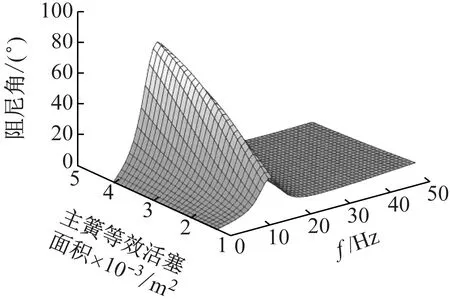
圖16 橡膠主簧等效活塞面積對液壓懸置阻尼角影響Fig.16 Influence of equivalent piston area of rubber main spring on damping angle of hydraulic mount

4.3 上下液室體積剛度對懸置動特性的影響

上液室的等效體積剛度對液壓懸置的動剛度和阻尼角影響很大，如圖17、18所示。上液室的體積剛度變化范圍為[1，3]×1010N/m5，隨著上液室等效體積剛度的增大，懸置動剛度和阻尼角都會大幅增大，同時還引起動剛度和阻尼角峰值頻率的改變，動剛度峰值頻率從13 Hz增大到20 Hz，阻尼角頻率從8 Hz增大到13 Hz，這對空氣彈簧液壓懸置動剛度和阻尼角曲線的設計具有重要意義。

圖18 上液室等效體積剛度對液壓懸置阻尼角影響Fig.18 Influence of equivalent volume stiffness of upper chamber on damping angle of hydraulic mount

下液室的體積剛度在[2.5，7.5]×108N/m5范圍內變化時，如圖19、20所示，對液壓懸置的動特性幾乎沒有影響。因為下液室的主要功能是容納液體，而非力學作用，下液室體積剛度需要與上液室體積剛度拉開數(shù)量級，否則將對液壓懸置動特性產生干擾。

圖19 下液室體積剛度對液壓懸置動剛度影響Fig.19 Influence of volume stiffness of lower chamber on dynamic stiffness of hydraulic mount

4.4 慣性通道內液體特性對懸置動特性的影響

慣性通道內液體的質量慣性系數(shù)主要影響懸置的動剛度和阻尼角出現(xiàn)峰值的頻率，即慣性系數(shù)越大，懸置的峰值頻率越小，這一點可以從圖21、22中動特性峰值的曲線扭曲程度和扭曲方向可以看出，當液體的質量慣性系數(shù)從1.25×106kg/m4增大到3.75×106kg/m4時，動剛度峰值頻率從23 Hz提前到13 Hz，阻尼角頻率從15 Hz提前到9 Hz。

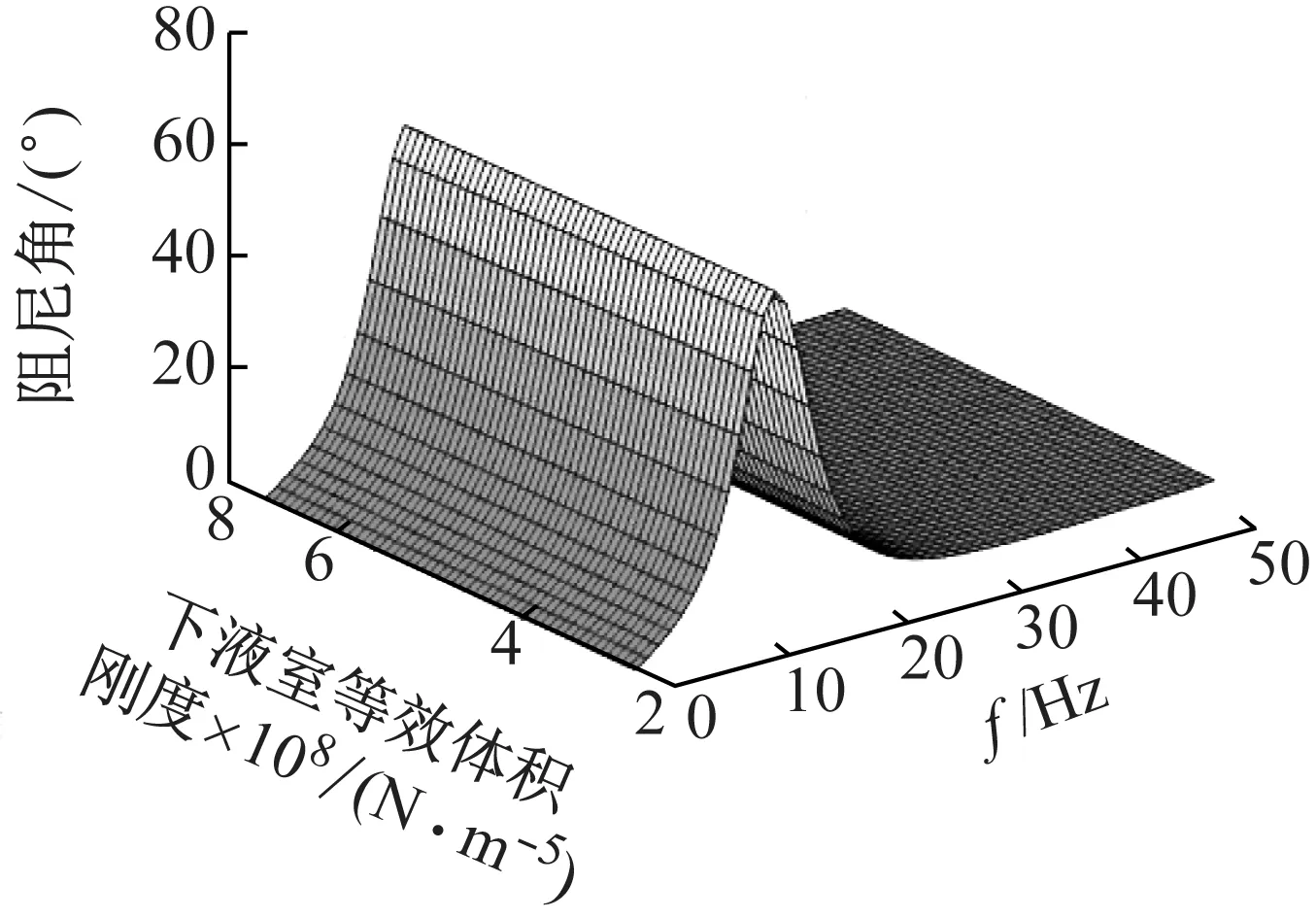
圖20 下液室體積剛度對液壓懸置阻尼角影響Fig.20 Influence of volume stiffness of lower chamber on damping angle of hydraulic mount

圖21 慣性通道內液體慣性系數(shù)對液壓懸置動剛度影響Fig.21 Influence of liquid inertia coefficient of inertia track on dynamic stiffness of hydraulic mount

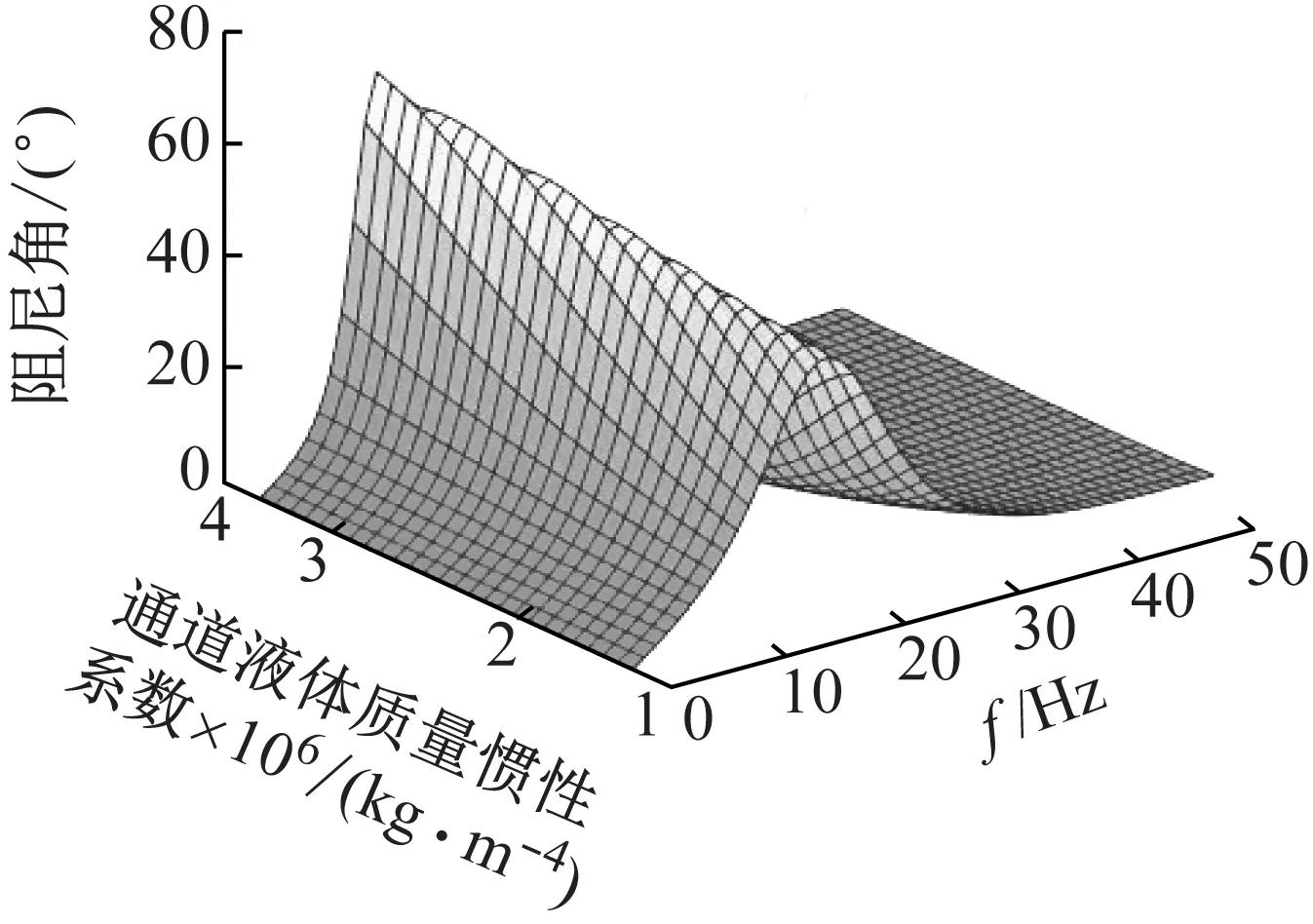
圖22 慣性通道內液體慣性系數(shù)對液壓懸置阻尼角影響Fig.22 Influence of liquid inertia coefficient of inertia track on damping angle of hydraulic mount

慣性通道內液體的流量阻尼系數(shù)在[0.5，1.5]×108N·s/m5變化時，只對液壓懸置動剛度和阻尼角的峰值大小產生影響，即流量阻尼系數(shù)越小，液壓懸置的動剛度和阻尼角的峰值越大，如圖23、24所示。

將空氣彈簧懸置動剛度的峰值變化量ΔSi與該空氣彈簧懸置原始參數(shù)(如表1所示)情況下懸置的峰值動剛度Smax的百分比，用于衡量該參數(shù)對懸置動剛度影響程度，用s1表示，表達式為

(13)

將空氣彈簧懸置阻尼角的峰值變化量ΔAi與該空氣彈簧懸置原始參數(shù)(如表1所示)情況下懸置的峰值阻尼角Amax的百分比，用于衡量該參數(shù)對懸置阻尼角影響的程度。用s2表示，其表達式為

圖23 慣性通道內液體阻尼系數(shù)對液壓懸置動剛度影響Fig.23 Influence of liquid damping coefficient in inertial channel on dynamic stiffness of hydraulic mount

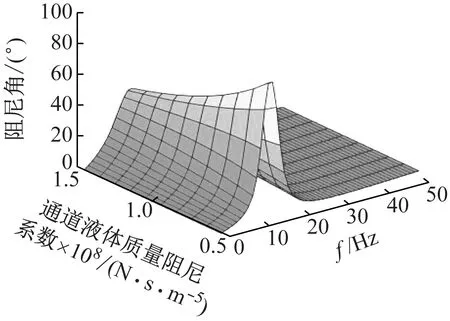
圖24 慣性通道內液體阻尼系數(shù)對液壓懸置阻尼角影響Fig.24 Influence of liquid damping coefficient in inertial channel on damping angle of hydraulic mount

(14)

將圖11～圖24仿真值代入式(13)、(14)后，得出各參數(shù)對空氣彈簧懸置的動剛度和阻尼角影響程度如圖25、26所示。圖中峰值靈敏度正值表示隨著參數(shù)的增大，動剛度增大或阻尼角增大即正相關，負值表示隨著參數(shù)的增大，動剛度增大或阻尼角減小即負相關。

a-橡膠主簧動剛度;b-橡膠主簧阻尼;c-橡膠主簧等效活塞面積;d-上液室體積剛度;e-下液室體積剛度;f-慣性通道內液體質量慣性系數(shù);g-慣性通道內液體流量阻尼系數(shù)
圖25 各參數(shù)對動剛度峰值靈敏度
Fig.25 Peak value sensitivity of each parameter to dynamic stiffness

由圖25、26可以看出：

(1)橡膠主簧等效活塞和上液室體積剛度對懸置動剛度和阻尼角的靈敏度最大，達到76%以上，并且是正相關的關系，因此適當增大橡膠主簧等效活塞面積和上液室體積剛度有利于懸置的低頻隔震。

圖26 各參數(shù)對阻尼角峰值靈敏度Fig.25 Peak value sensitivity of each parameter to damping angle

(2)隨著橡膠主簧動剛度的增大，懸置的動剛度增大，但是懸置阻尼角減小，不利于懸置的低頻隔震，因此在空氣彈簧設計時橡膠主簧的動剛度不宜太大。

(3)橡膠主簧的阻尼和下液室的體積剛度對空氣彈簧懸置的動剛度和阻尼角幾乎沒有影響，在懸置動特性設計時，可以不作為主要因素考慮。

(4)慣性通道液體質量慣性系數(shù)對空氣彈簧懸置動剛度和阻尼角是正相關關系，而慣性通道內液體流量阻尼系數(shù)對空氣彈簧懸置動剛度和阻尼角是負相關關系，為此適當增大慣性通道液體質量慣性系數(shù)，減小慣性通道液體流量阻尼系數(shù)有利于懸置的低頻隔震。

5 結 論

(1)本文采用空氣彈簧液壓懸置上液室等效體積剛度替代解耦膜以及密閉空氣腔對懸置動特性的影響，基于流體力學相關理論建立的空氣彈簧液壓懸置力學模型，通過試驗驗證表明該模型可以較好的反映空氣彈簧液壓懸置的動態(tài)特性。

(2)空氣彈簧液壓懸置的動剛度和阻尼角在空氣腔開閉兩種狀態(tài)下，其變化范圍較大，在空氣腔關閉時，空氣彈簧懸置表現(xiàn)出大剛度大阻尼特性，動剛度達到最大值480 N/mm，阻尼角最大值62°，當空氣腔開啟時，空氣彈簧懸置表現(xiàn)出小剛度小阻尼特性，動剛度最大值僅有300 N/mm，阻尼角最大值僅有30°。比較空氣腔開啟和空氣腔關閉兩種狀態(tài)，動剛度增大了60%，阻尼角增大了106%，可以有效的進行發(fā)動機各種工況下的振動控制。

(3)基于該模型對影響空氣彈簧液壓懸置動特性主要參數(shù)進行了靈敏度分析，得到了各參數(shù)與動剛度和阻尼角的變化關系，為空氣彈簧液壓懸置動特性優(yōu)化設計提供了參考。