基于EKF-LESO級聯觀測的永磁直線同步電機無傳感器線性自抗擾控制

董家臣,高欽和,陳志翔，牛海龍

(火箭軍工程大學 兵器發射理論與技術國家重點實驗室，西安 710025)

“零傳動環節”是永磁直線同步電機異于旋轉電機的突出結構特點，在賦予電機高推力電流比、高定位精度、高傳動效率等優勢的同時，也因對擾動的過分敏感而為高精度伺服系統的設計帶來困難。電機伺服系統要取得良好的控制效果，依賴于反饋的動子狀態信號的品質。目前其位置檢測多采用光柵尺、磁柵尺等，這些機械傳感器反饋回的狀態信息不可避免地受到了噪聲的污染，在響應速度要求較高的場合下極易誘發直線電機抖振的產生。與此同時，傳感器對環境的溫、濕度要求較為苛刻，其使用不僅會增加電機的設計成本和維護成本，還會改變氣隙寬度，干擾電機的電感和磁場分布、降低系統的平穩性和可靠性。因此，尋求合適的狀態估計算法，實現PMLSM的無傳感器控制成為當前研究的熱點[1-2]。

直線電機的動子與定子間氣隙較大，交直軸電感近似相等，基于凸極效應的高頻信號注入法并不適用，基于定子磁鏈的反電勢估算技術成為當前的主流研究方向。孔龍濤等[3]將模型參考自適應法(Model Reference Adaptive System,MRAS)應用在模塊化磁通切換永磁直線電機的位置估算中，獲得了良好的實驗控制效果，但該方法對系統數學模型的準確性要求較高；Wang等[4]應用滑模觀測器(Sliding Model Observer,SMO)+鎖相環(Phase Locked Loop,PLL)設計了電機的速度估算回路，并引入自適應濾波器減小SMO的抖振以及磁場諧波影響，最終獲得了出色的運行平穩度和控制精度，但整個系統設計復雜，對硬件要求很高；韋文祥等[5]使用ESO辨識轉子磁鏈，進而結合MRAS估算轉速，明顯優點在于消除了純積分環節的影響，對低速區仍有較高的轉速辨識精度，但幾種控制方法疊加嵌套使得系統響應較慢。作為基于最小方差估計理論發展起來的一種算法，擴展卡爾曼濾波能有效權衡系統噪聲和測量噪聲、甚至模型參數不確定度在內的干擾，實現對系統狀態的有效估計。將EKF應用于電機運行狀態的估算中，獲得的估計值較真實值能夠具有更少的噪聲引入，反饋的信號更平滑[6-7]，有利于減輕控制率突變帶來的系統抖振，提高反饋控制系統的平穩性。

電機在運行中，電氣信號的品質對電機狀態的估算亦存在較大影響，尋求合適的控制策略對伺服系統平穩控制效果的獲取同樣至關重要。PMLSM在實際運行中，負載變化、推力波動、磁場畸變等均會對動子的運行狀態產生影響，這些擾動的隨機性、非線性特征較強，對其建模極為困難，使得諸多基于模型的控制策略無法適用。中科院韓京清教授提出的自抗擾控制(Active Disturbance Rejection Control,ADRC)[8-11]是一種不依賴擾動模型的實用控制技術，在繼承PID“基于誤差消除誤差”反饋思想的同時，通過設計擴張狀態觀測器(Extended State Observer,ESO)實時觀測“總擾”，并對控制量進行反饋補償，可以對包括系統內擾和外擾在內的“總擾”項實施更為高效的抑制，從而大大增強系統的穩定性和魯棒性。Gao[12]基于帶寬思想進一步將ADRC以線性形式實現，大大減小了參數整定的難度，使得線性自抗擾控制(LADRC)具備了廣泛工程應用的可能[13-16]。在控制系統的構建中，線性ESO是LADRC的重要組件之一，用于為控制器提供反饋量，但實際上同樣有著出色的信息提取能力，通過整定觀測帶寬能夠以較高精度觀測系統的各階狀態。

因此，為實現PMLSM的平穩運行,同時擺脫速度傳感器的限制，本文提出了一種基于LESO與EKF級聯觀測的永磁直線同步電機無傳感器線性自抗擾控制策略。首先對LESO的觀測誤差進行理論分析，得出在輸入量測信號存在慢時變偏差的情況下，LESO具有從中提取“中階狀態”(2～n)信息的能力，具有一定的容錯性。進而以此為依據，提出了EKF+LESO的級聯觀測方式，搭建了無傳感器線性自抗擾控制系統。最后設計仿真和實驗，對LESO的容錯能力、系統對不同期望輸入的跟隨能力、整個系統的抗擾能力以及在環境噪聲存在的情況下，系統的運行平穩性進行了驗證。

1 PMLSM的線性自抗擾控制

1.1 PMLSM建模

永磁直線同步電機由旋轉電機演化而來，將旋轉電機沿徑向剖開、展平，即得到直線電機的基本結構雛形，如圖1所示。

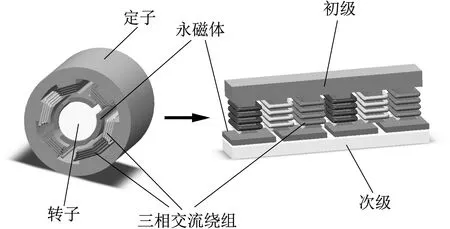
圖1 PMLSM的結構演化Fig.1 Structural change from PMSM to PMLSM

結構的相通性使得可以使用旋轉電機的模型分析理論來對直線電機進行類比建模。由于電機初、次級之間氣隙較大，在d-q坐標系下通常將電感值做Ld=Lq=L處理。在不考慮齒槽效應、磁路飽和、鐵心損耗、推力波動、磁場空間諧波等次要因素，且反電勢為正弦波、轉子無阻尼繞組的情況下，PMLSM在轉子d-q坐標系下的電壓方程可以表述為

(1)

電磁轉矩方程為

(2)

運動方程可由牛頓第二定律給出

(3)

式中：iq為定子繞組的q軸電流；Ψf為永磁體磁鏈，Te、Tl為電磁轉矩、負載轉矩；B為黏滯摩擦因數；ω為動子等效到旋轉坐標系下的電角速度，ω=πυ/τ，υ為動子速度、τ為極距(同樣，后文提到的θ為等效電角度)；J為動子等效轉動慣量，np為極對數。

聯立式(2)、(3)，并考慮實際建模誤差，可得到PMLSM伺服系統的位置環運動方程

(4)

這里，Δw表征簡化處理帶來的系統未建模部分以及建模不準確部分。

1.2 LADRC系統設計

(5)

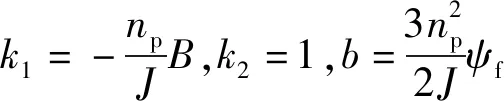
按照經典ADRC中忽略h的構建原則，建立LESO如下

(6)

將結果整理成矩陣形式

(7)

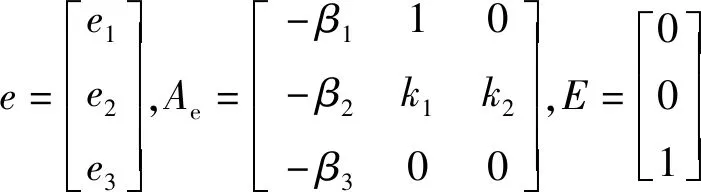
式(7)的特征方程為

λ(s)=λ3+(β1-k1)λ2+(β2-k1β1)λ+k2β3

(8)

依據Lyapunov第一穩定判據，為保證系統的觀測穩定性，特征值應全部位于左半平面。同時，為便于參數調節，結合文獻[12]基于帶寬思想的參數整定方法，將式(8)配成λ(s)=(λ+wo)3的理想形式(wo為設置的觀測器的帶寬)，得到觀測器增益

(9)

考慮按如下形式設計反饋補償環節

(10)

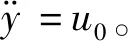
(11)

這樣，在頻域內將等效后的積分器串聯標準模型與控制器模型聯立

(12)

可以解出線性狀態誤差反饋控制率(LSEF)為

(13)

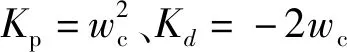
至此，式(6)、(9)、(10)、(13)即構成LADRC系統的主體。其原理圖如圖2所示。

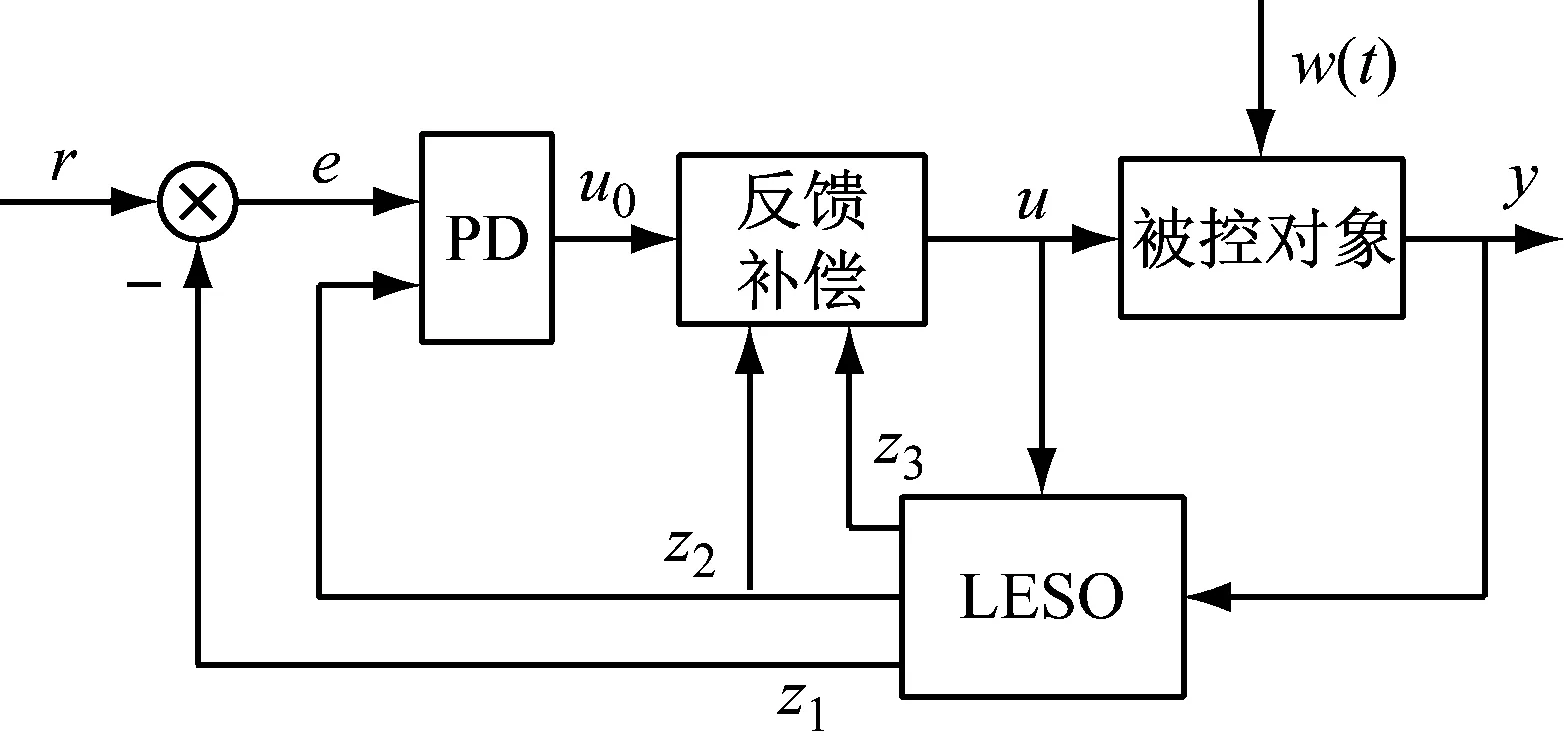
圖2 LADRC結構示意圖Fig.2 A common LADRC scenario

2 LESO的容錯性討論

擴張狀態觀測器是自抗擾控制的核心部件，通過對系統各階狀態準確、迅速地觀測，為整個閉環系統的控制提供反饋量。目前的文獻對其收斂性、觀測誤差有界性、濾波能力做出了較多研究[17-19]，但對其從輸入量中提取狀態信息的能力鮮有討論。為此，本節主要討論在輸入LESO的量測信號存在慢時變偏差的情況下觀測器的容錯能力。

2.1 LESO的觀測精度分析

閉環反饋系統的控制量以PD形式輸出，這種控制無靜差的前提是LESO有足夠的觀測精度使被控對象可等效為積分串聯標準型；同時總擾項的反饋補償環節也依賴于LESO。因此，LESO的觀測能力直接決定了LADRC系統的控制精度。觀測值與PMLSM狀態真值之間的偏差主要由兩部分構成：

2.1.1 結構誤差

與此同時，LESO的擴張狀態采取了忽略擾動模型的處理方式，擺脫了對系統的依賴性的同時也使得誤差系統引入了Eh項，式(7)的結構形式是非齊次的，因此觀測必然存在穩態誤差，且其大小與擾動的變化成正比。

2.1.2 量測誤差

無傳感器控制將動子位置信息的獲取由傳感器變更為位置估算，算法通過處理實時測得的電氣信號換算出θ值，受運行噪聲、算法性能的影響，輸入LESO的y會存在一定偏差，從而對LESO的觀測準確性產生影響。

針對上述誤差，在系統運行平穩性能得到保證的前提下，盡可能增大觀測器帶寬wo可以獲得更快的觀測速度和更高的觀測精度，而選擇高性能的無傳感器估計算法是減小量測誤差的有效辦法。

2.2 LESO的容錯能力分析

不失一般性，考慮一類SISO(Single-Input-Single- Output)的n階時變系統

(14)

式中：w(t)為與時間有關的未知外界擾動，其微分項h(t)存在且有界；u為系統的控制輸入；y為系統輸出；b為控制增益。

考慮輸入量存在慢時變偏差對系統各階狀態的觀測帶來的影響，此時y1=x1+Δθ(t)

按照1.2節思路設計LESO，同樣可以獲得n+1階誤差矩陣方程

(15)

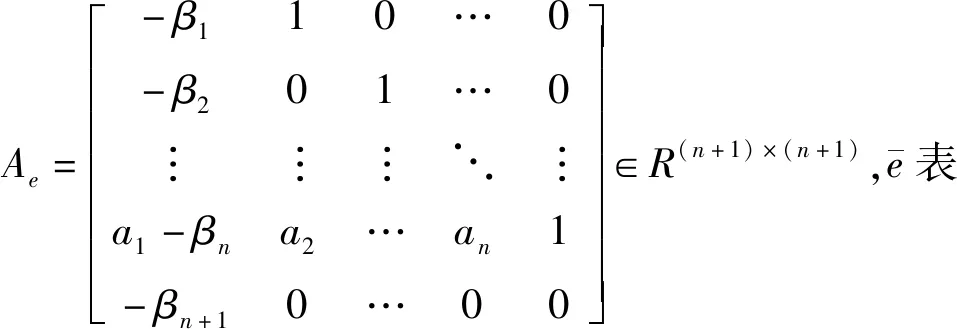
(16)

(17)

該方程在形式上與模型(7)是一致的，帶寬wo使其特征方程同樣滿足Lyapunov第一穩定條件。為進一步簡化分析，做如下假設

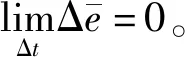
假設2Δθ(t)有界且為慢時變增量，在LESO的單次觀測中可視為恒值Δθ。

假設1、2本質上是不考慮誤差的動態收斂過程，這樣在步長Δt內的單次觀測中，有

AeΔe+LΔθ=0

(18)

將該n+1階矩陣方程展開、聯立，可解出觀測精度的穩態耗損量最終表達式

(19)

可見，雖然在結構上LESO對各階狀態的觀測均依賴e1趨于0的收斂，但當e1中含有慢時變偏差Δθ時，觀測器對第2～n階的狀態觀測并不受影響，其觀測精度仍然不變。

結論LESO具有一定的容錯性，在輸入量測信號存在慢時變偏差時，仍能對中階(2～n)狀態實現有效的觀測，且觀測精度不受這種偏差的影響。

3 無速度傳感器算法的實現

3.1 基于EKF算法的動子位置估算

EKF算法以最小均方差原理為基礎，通過每一步遞推在估算變量的同時實現系統噪聲、量測噪聲協方差矩陣的實時更新，因而具有出色的環境適應能力和噪聲抑制能力。過去由于算法計算量大而限制了其應用范圍，但如今處理器芯片的計算能力已經能滿足其需求。因此，本文選擇EKF作為PMLSM動子位置信號的估計算法。

PMLSM在αβ坐標系下的電壓方程可以表述為

(20)

從而將模型(22)擴展為如下矩陣形式

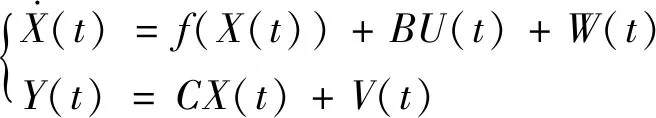
(21)

W、V為0均值，方差矩陣分別為Q、R的高斯噪聲，代表系統狀態轉移噪聲向量和測量噪聲向量，與X不相關。初始狀態向量為具有均值X0、方差P0的高斯隨機向量。比對模型(22)，可得非線性項

(22)

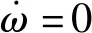
對式(24)做一階泰勒展開可得雅克比矩陣

(23)

系統離散化(h為步長)，可得

(24)

基本離散型EKF狀態估計算法如表1所示。

表1 EKF算法Tab.1 EKF algorithm

3.2 級聯觀測系統設計

EKF算法使用電機的定子電壓和電流估算速度和位置信息，考慮運行噪聲時變、磁場畸變干擾、初始位置估算不準引入偏差等影響，在設定先驗噪聲矩陣時通常取較大值，此時轉速的估計精度會下降。在長時間運行過程中，電壓、電流傳感器等電子元器件的老化、積分器零漂引入的直流偏差也是導致估算的電機狀態信息不準確的重要原因。

采用合適的控制策略能夠抑制系統內部的擾動，從而可以在一定程度上提高EKF對系統狀態的估計精度[20-22]。與此同時，第二節中分析了LESO的容錯性，因此可以與其他變量估計算法進行串聯，以從含偏差的估計量中提取“中階狀態”信息。因此，本文選擇抗擾性能出色的LADRC作為PMLSM的控制策略，在速度辨識上，選用LESO+EKF的級聯觀測方式。由于觀測帶寬既影響LESO的觀測精度，又決定著LADRC系統的控制精度，因而通過整定wo，在獲得高精度速度信息的同時，也能提高伺服系統的控制精度。

對PMLSM的電流環，將式(1)變形為

(25)

可見，如果設計udeq、uqeq為控制量，電壓模型將不存在耦合，此時非線性環節ωLiq、-(ωLid+ωΨf)需作為前饋補償項等效進控制量中，進而可以將模型轉化為線性系統進行控制。

基于id=0的矢量控制策略，選擇應用較廣的PI控制構建電流內環伺服回路，在反饋量的選擇上，補償項的轉速反饋量應選取LESO的估計值。由于LESO對輸入量y=x1沒有校正能力，且EKF濾波效果較好，動子位置應以EKF估計值為準。LESO在電機狀態的級聯觀測中承擔校正轉速估值的作用，同時在整個LADRC系統中作為總擾項的反饋源，為控制量提供反饋信息。

最終設計的無傳感器控制系統如圖3所示。

4 仿真及實驗

為驗證本文所提出的級聯觀測系統的可行，在Matlab2015b/Simulink環境下按圖3搭建了仿真系統，針對LESO的容錯能力、系統對不同期望輸入的跟隨能力、整個系統的抗擾能力進行仿真驗證。進而基于DSP28335的PMLSM控制平臺，通過實驗進一步驗證真實環境下(電機模型含不缺定度、系統存在噪聲)級聯觀測的有效性以及直線電機無傳感器線性自抗擾控制系統的運行平穩性。

4.1 仿 真

仿真模型建立在第一節中的等效旋轉坐標系下，參數設置如表2所示。

4.1.1 LESO的容錯性驗證

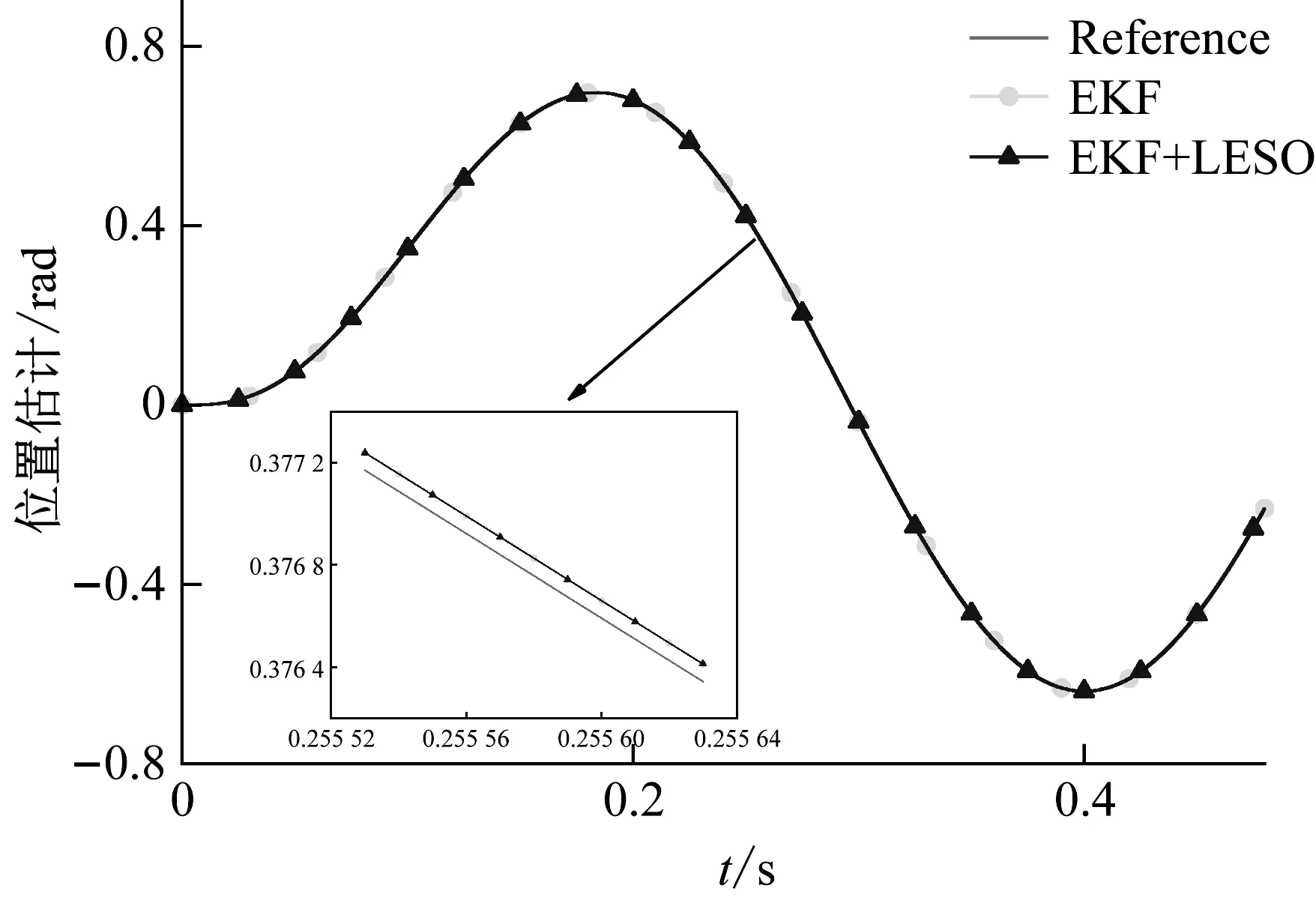
在轉速辨識的仿真中，設定期望轉子信號為單位幅值、頻率為15 Hz的正弦信號，在EKF辨識出的轉子位置信號輸入LESO的過程中人為加載恒值偏差(y，觀察系統的級聯觀測情況。圖4的仿真結果表明，設計的無傳感器LADRC系統能夠正常運行，由圖4(a)可見，在對轉子位置信號的估計上，EKF算法存在一定的觀測滯后，這是數字濾波器無法避免的缺點，級聯的LESO只是跟隨EKF的估計值，并不產生修正作用，因此整個系統的估計精度由EKF決定。由圖4(b)則明顯看出，在對“中階狀態”——轉速的估計上，LESO從轉角中提取出的轉速要明顯優于EKF對轉速的直接估計值，同時相位滯后大大減輕，對轉速的跟蹤精度得到近十倍的提高。

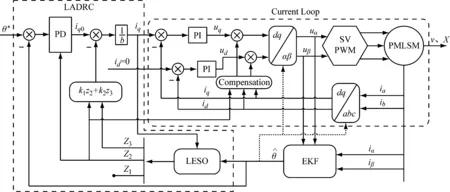
圖3 基于EKF-LESO級聯觀測的LADRC系統設計圖Fig.3 The sensorless LADRC system with EKF-LESO

表2 仿真參數Tab.2 Simulation parameters

(a)

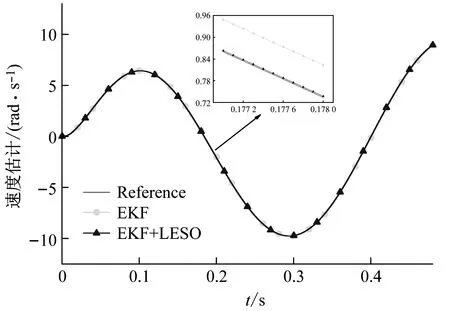
(B)圖4 級聯觀測的狀態估計曲線Fig.4 State estimation curve of cascading observation

圖5進一步給出了在EKF提供的轉角“粗估計值”存在直流偏差Δy=0.2時對轉速的級聯觀測情況。EKF的粗估計最大誤差為-0.102 6，遠大于EKF+LESO (0.004 7)，可見級聯觀測的精度仍有較大提高。

4.1.2 系統跟隨能力、抗擾能力驗證

圖6給出了設計系統對不同期望位置信號(單位常值信號，單位幅值、頻率20 Hz的正弦信號)的跟隨曲線，在一定程度上反映了整個系統的控制性能。對常值信號的跟隨過程平穩無超調，跟蹤精度較高(誤差為5.34×10-4)。在對定頻信號的跟隨上則出現了明顯的相位滯后，增大控制器帶寬wc則能有效減輕滯后的影響，這是因為整個LADRC按照模型(11)等效，其跟隨規律符合自動控制原理中二階系統的頻響關系。同時這種構建方式省去了速度環控制，更利于控制上滯后程度的減輕。

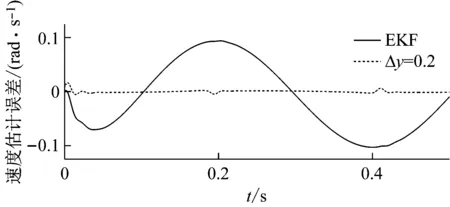
圖5 轉速級聯觀測的誤差曲線Fig.5 Cascading observation error of speed

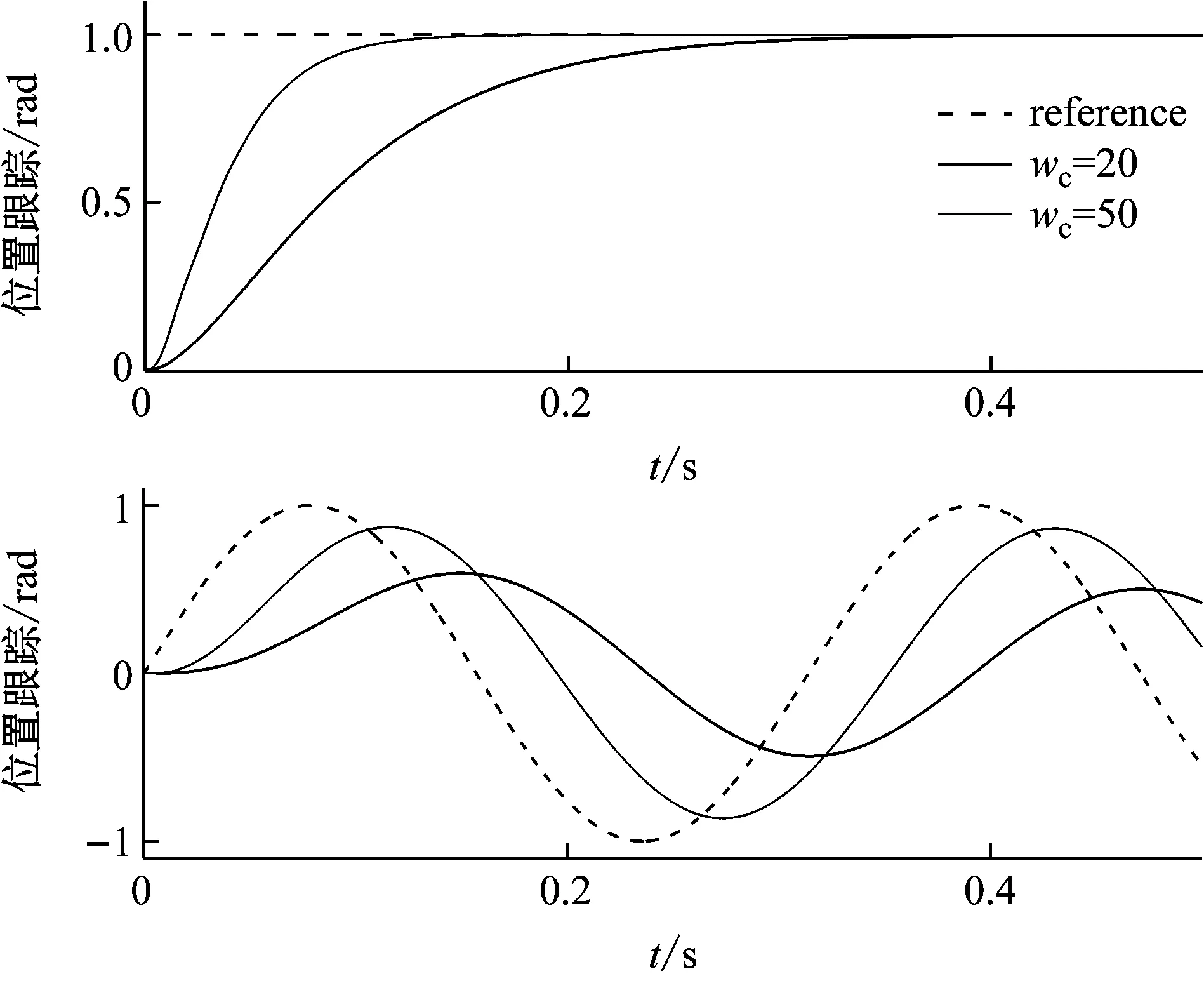
圖6 位置跟隨曲線Fig.6 Position tracking curve

針對PMLSM敏感擾動的特點，在常值期望輸入下做了LADRC與三環PI的抗擾對比仿真，擾動為幅值1 N·m、在0.3 s階躍的負載力矩。位置環與速度環的PI參數分別為[30,2]、[0.7,20]。圖7給出了跟蹤對比情況，在響應速度上PI控制占據優勢，這是由于經典PI控制多串聯了速度環的控制器，因此在動態控制上靈活性、可控性較強，但同時也存在參數整定繁瑣的弊端。加載擾動后，顯然LADRC的擾動抑制能力更出色，調節時間更快，這是由自抗擾控制的本質特征決定的——通過觀測和實時反饋，將原來PI控制恒定速率的誤差收斂變為直接從初始控制量中減去總擾項，從而大大加快了控制量的調整速度，使得系統應對突變擾動有著更快的響應表現，從而提高了整體的擾動抑制效果。

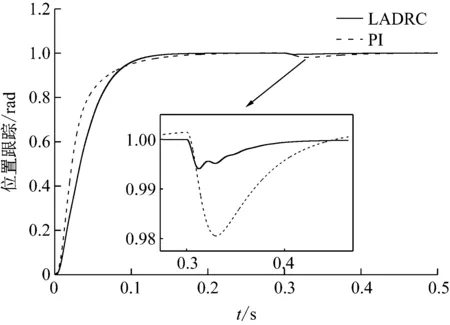
圖7 位置跟隨曲線(含擾動)Fig.7 Position tracking curve (with disturbance)

4.2 實 驗

實驗中使用了北京靈思創奇公司生產的仿真器及研發型交流伺服驅動器。仿真器中集成了Ti公司的DSP芯片TMS320F28335，在MATLAB/Simulink中使用DSP仿真包搭建控制模型，編譯、下載至仿真器中。驅動器選擇IGBT-PWM模式，支持DSP輸出的PWM波直接控制逆變器，基于空間電壓矢量調制技術為PMLSM提供驅動電壓。逆變器死區設置2.3 μs，直流端電壓使用穩壓電源30 V。為保證足夠的EKF運算時長，相電流與位置采樣頻率分別設置5 kHz、1 kHz。系統中安裝了精度為±2((m的光柵尺為速度估計提供參考。實驗系統搭建如圖8所示。

PMLSM為U型槽直線電機，具體系統參數：R=5.84 Ω，L=3.65 mH，Ψf=0.118 2 Wb，np=4，B=1.2 N·m/s，τ=16 mm，m=3.8 kg。受環境噪聲影響，wo取150，wc設為30，不使用濾波器。電流環PI控制器取為[0.02,32]。

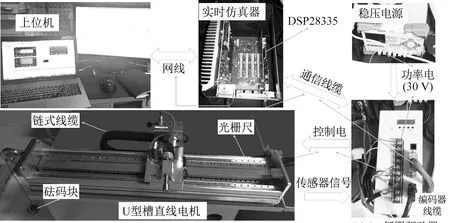
圖8 PMLSM實驗系統Fig.8 Laboratory test system of PMLSM

為針對性驗證LESO的容錯能力，EKF算法取為如下噪聲矩陣：Q=diag[20,20,200,0.1]，R=diag[0.2,0.2]，比較速度估計效果及控制精度。

設計期望位置信號，使得速度在0～2.5 s、2.5～5 s分別以8、-8 mm/s3的加加速度運行，最終穩定在50 mm/s。圖9給出了動子運行速度曲線，在加速過程中，EKF的估計值始終與真值偏差較大，且相位嚴重超前，LESO的估計值則能始終以較高的精度逼近真值。圖10顯示的估計誤差更能直觀表明這一點。10 s時刻電機開始拖動砝碼塊(0.25 kg)，動子速度出現了約0.5 mm/s的降幅，隨后產生了震蕩，這一過程中EKF對速度的估計出現了靜差，震蕩的均值速度約為53.7 mm/s，而LESO始終圍繞真實速度，在50 mm/s處震蕩，但振幅較EKF(0.282)大很多(1.193)。可見，EKF具有出色的濾波能力，雖然由于噪聲矩陣的設置使其估計精度并不高，但經過LESO后速度的觀測得到了校正，這也驗證了LESO從含較大偏差的信號中提取中階狀態信息的“容錯能力”。

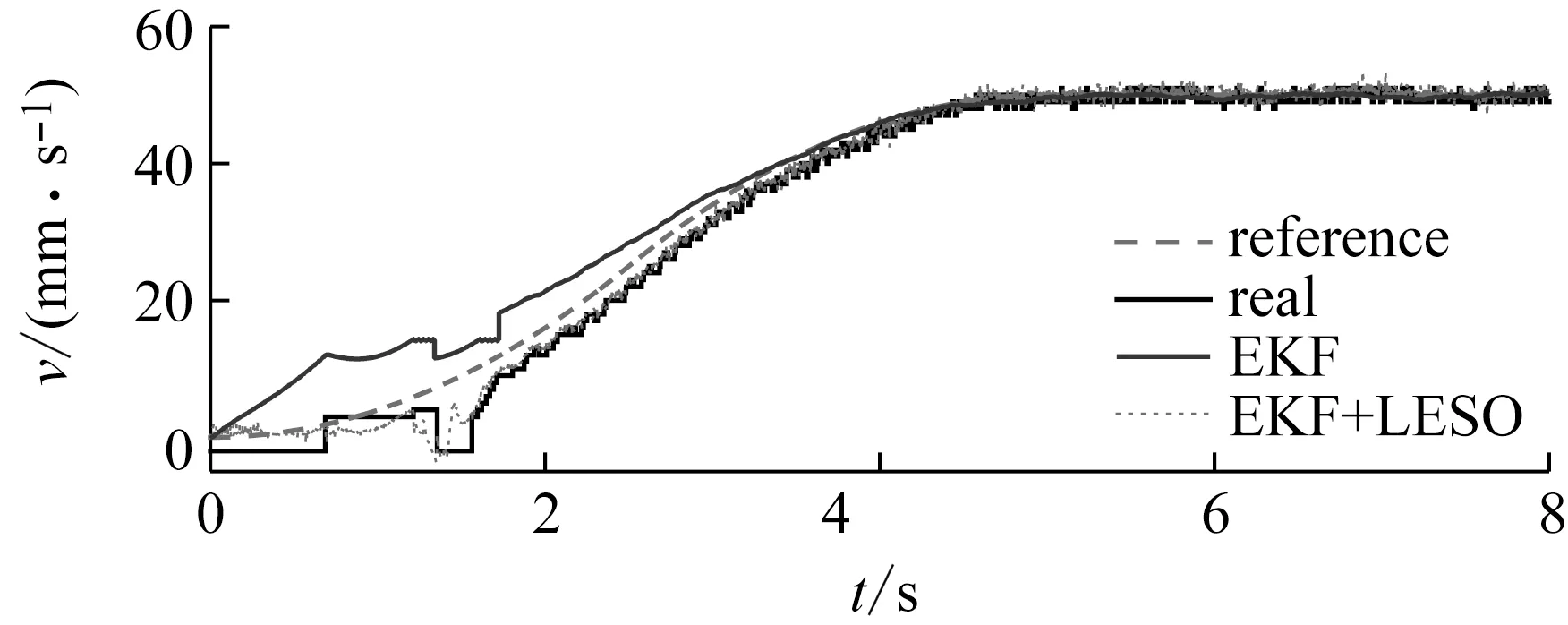
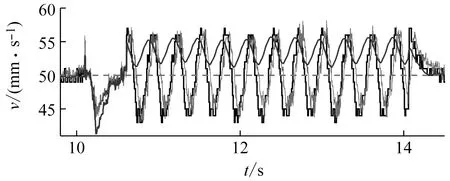
圖9 動子速度曲線Fig.9 Speed curve of motor driver

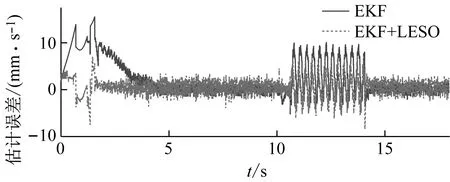
圖10 速度跟蹤誤差、估計誤差曲線Fig.10 Speed tracking and estimating error

對比電機真實運行速度與規劃速度，在起步階段，由于靜摩擦的存在，實際速度與期望速度之間存在較大誤差，前1.8 s追蹤明顯滯后，隨后系統能夠按照規劃軌跡穩定運行，速度跟蹤誤差不超過±1.5 mm/s(圖9)。帶載運行時，系統出現了一定幅度的震蕩(5.6 mm/s)，一部分原因在于未使用濾波器的緣故使得wo取值較小，觀測精度受限，同時wc整定值較小，系統抵抗負載等擾動的剛度不夠；另外為驗證級聯觀測的有效性，EKF的估計精度也調得較低。但系統始終能夠圍繞期望速度穩定運行。

圖11、12給出了在規劃速度信號為幅值80，頻率0.5的正弦信號輸入下，級聯觀測系統的速度估計對比及整個PMLSM伺服系統的運行曲線。LESO對速度的觀測引入了較多的噪聲，但其均值始終跟隨真值，這與圖9、10的分析結論是一致的。注意到在6.4 s左右速度趨近0，此時LESO的觀測出現了明顯的“峰化現象”，這是擴張狀態觀測器的固有弊端。這種誤差經反饋傳遞至控制率中，最終引起系統控制精度的突降(圖12中控制誤差由8 mm/s增至約20 mm/s)，對伺服系統的控制效果存在不利影響。但總體而言，在EKF取較差精度、不使用濾波器的前提下，整個無傳感器控制系統依然能夠平穩運行，體現出級聯觀測的有效性以及伺服系統較強的抗擾能力。

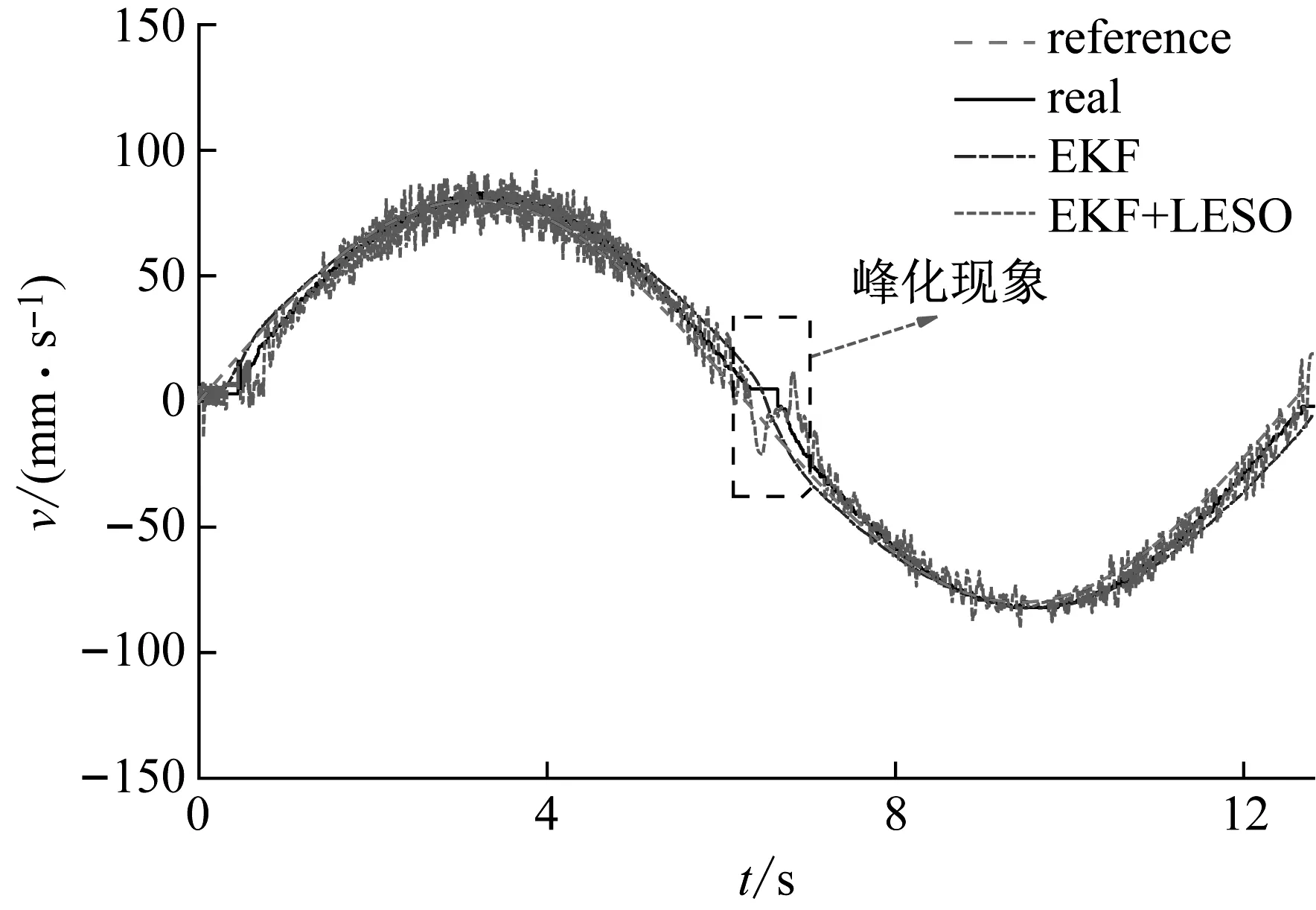
圖11 速度曲線(幅度80，頻率0.5 Hz)Fig.11 Speed curve of sin signal (80,0.5 Hz)

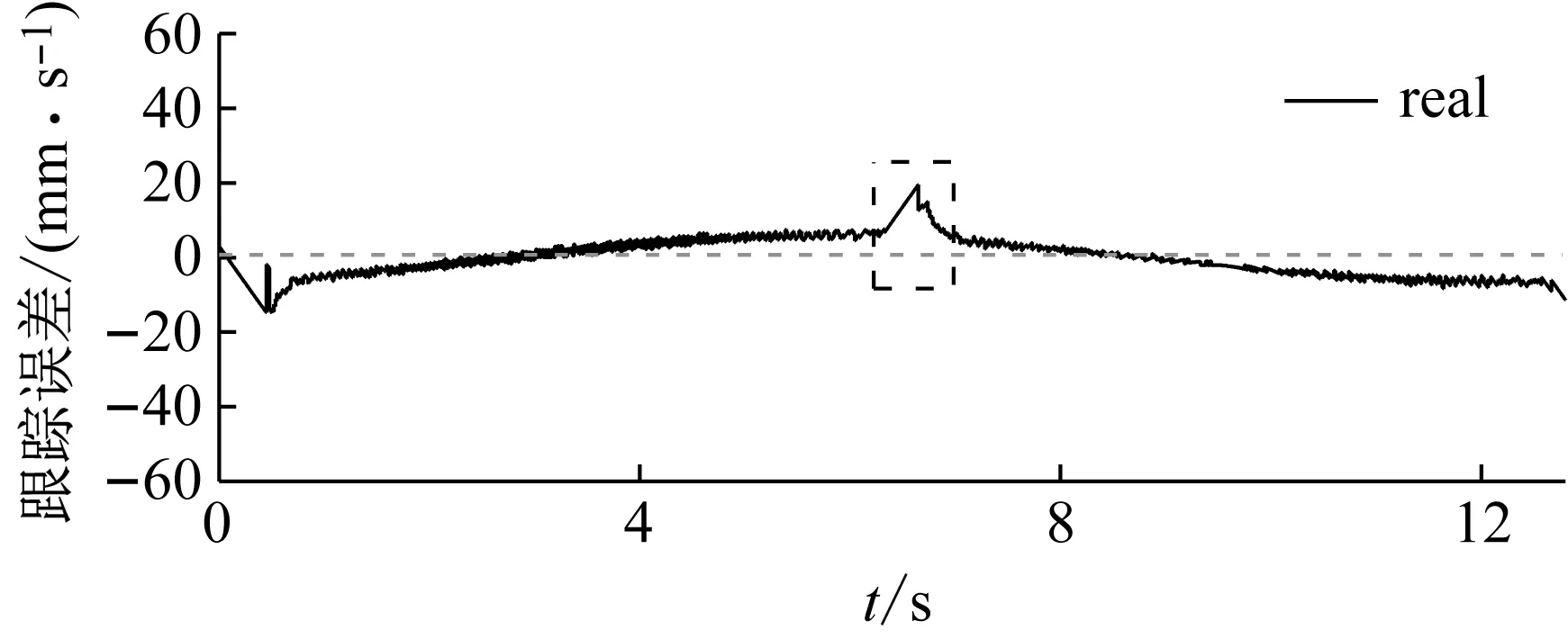
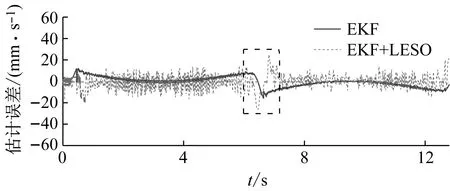
圖12 速度跟蹤誤差、估計誤差曲線Fig.12 Speed tracking and estimating error

5 結 論

為提高直線電機伺服系統的抗擾能力，抑制電機抖振的產生，設計了PMLSM的位置環線性自抗擾控制系統。為進一步擺脫速度傳感器的束縛，在分析LESO觀測精度的基礎上，通過理論推導，得出在輸入量測信號存在慢時變偏差的情況下LESO對中階(2～n)狀態的觀測不受影響、具有一定容錯能力的結論，進而提出了一種EKF+LESO的無傳感器速度級聯觀測方式。仿真驗證了LESO的容錯性、級聯觀測系統對速度估計的準確性以及新系統的抗擾能力；實驗結果則進一步表明，在建模不確定度、環境噪聲客觀存在的條件下，新系統能夠對速度實現較高精度的觀測，系統抗擾能力較強，具有良好的運行平穩性。針對LESO觀測過程中出現的峰化現象，設計有效的抑制策略是下一階段研究的重點。