基于能量有限元法的損傷充液管道振動分析

尚保佑 ，朱 翔，李天勻 ，梁孝天

(1.華中科技大學 船舶與海洋工程學院，武漢 430074；2.船舶與海洋水動力湖北省重點實驗室，武漢 430074；3.高新船舶與深海開發裝備協同創新中心，上海 200240)

充液管道在工程領域中的運用非常廣泛。這些結構在服役期間會出現各類形式的損傷。針對管道結構開展早期的損傷識別研究具有重大的理論意義和實際價值。在結構損傷識別的研究中，基于結構振動特性的損傷識別法成為眾多科研人員關注的重點。周祥等[1]對主流的幾種損傷探測識別方法進行比較，并簡述了目前機械結構損傷識別領域中一些待解決的問題。劉景斌等[2]則在比較各損傷識別方法優劣性的基礎上，展望了未來損傷識別方法的發展趨勢。

結構中的振動波傳播和振動能量的傳播通常是結構物理參數，如剛度、質量和阻尼的函數，所以結構物理參數的變化會導致結構振動能量分布的變化。近年來基于振動能量的損傷識別方法得到了較多的關注。

Zhu等[3]對損傷Timoshenko梁和圓柱殼的振動功率進行了分析，提出了利用振動功率流[4]采用一局部轉動彈簧來模擬梁中的損傷，同時也利用斷裂力學的相關理論得到局部彈簧的轉動剛度。Santos等[5]認為結構中的損傷改變了能量耗散的結構，以能量流作為研究的基礎，用在研究梁結構的損傷識別和檢測中。隨后朱翔等[6]采用有限元法對裂紋損傷結構的功率流進行了相關研究并且引入了結構聲強的概念,以此實現了結構表面能量分布、傳播以及在裂紋位置周圍分布的可視化分析。Pang等[7]基于振動功率流理論，以呼吸裂紋板作為研究對象并對其輸入功率曲線進行分析。基于能量有限元法，王迪等[8]求解了損傷薄板結構的振動，并以結構聲強和能量密度為指標識別板結構中的損傷。能量有限元法(EFEA)是近些年發展起來的一種用于解決結構中高頻振動分析的方法[9]。它結合了統計能量法(SEA)和傳統的有限元法(FEA)的優點，是一種混合建模分析技術[10]。一方面，子系統可以通過網格的形式表現，另一方面，類似FEA的方法可通過節點描述能量的衰減過程。因此，對于結構的模態沒有過多要求，可以涵蓋中高頻段。Zhu等[11]利用有限元法和能量有限元法相結合的混合方法來預測結構在中頻部分的振動，通過算例獲得整個系統在不同區域的能量分布，驗證了所提出的方法可以用于在中頻范圍內的振動預測。劉知輝等[12]研究了三板耦合情況下的能量傳遞系數，并使用多種單元類型和混合單元等方法將能量有限元的應用拓展至任意復雜耦合結構[13]，并分析了由耦合板結構組成的封閉箱體。葛月等[14]研究了任意耦合角度下彎曲波、縱波和剪切波入射時特定入射角度下的能量傳遞系數，分析了耦合板結構中耦合角度、耦合板厚度、激勵頻率對能量傳遞系數的影響。解妙霞等[15]對能量有限元在復合材料結構動響應中的相關研究進行綜述。

國內外學者針對充液管道的振動開展了大量的研究。Tijsseling[16]對充液管道系統的流固耦合研究進展進行綜述。王琳[17]研究輸流管道的穩定性與非線性動力學機理，對管道的穩定性、分岔、混沌等特性進行了分析。包日東等[18]通過在模態空間展開運動控制微分方程的方法，分析了輸流管道振動系統的非線性動態響應。Luo[19]等利用微分求積法計算彎曲管道的非線性動力響應，闡述了微動磨損對管道損傷的影響。Zhou等[20]研究軸向功能梯度懸臂輸流管的線性動力學問題。

從查閱文獻來看，目前尚未有文獻建立充液管道結構振動分析的能量有限元方程，也沒有基于能量有限元法的充液管道結構損傷識別研究。本文首先推導建立了充液管道的能量有限元方程，然后基于能量有限元法對含有損傷的充液管道結構的振動特性進行分析。分別采用傳統有限元法和能量有限元法對管道中的能量密度進行了計算，驗證本文能量有限元法的正確性。通過分別改變含損傷充液管道中損傷部分的剛度、阻尼。計算充液管道在損傷前后的能量密度和能量流，并分析損傷參數與能量流之間的關系。

1 充液管道的能量有限元方程

1.1 充液管道的能量平衡方程

由文獻[21]可知，輸流管道的運動控制微分方程為

(1)

當不考慮管內流體流速帶來的影響即μ=U=0、P=T=0時，輸流管道運動方程退化為充液管道運動控制微分方程

(2)

式中：Ip是管道的截面慣性矩,Ep是管道材料的楊氏模量，ρp、Sp分別是管道的材料密度和橫截面積，ρf、Sf分別是管內流體的材料密度和橫截面積，η代表管道結構阻尼，w(x,t)表示管道的徑向位移，F代表激勵的幅值，δ代表狄拉克函數，x代表管道的軸向坐標，x0是激勵作用的位置，ω是圓頻率，t表示時間。

假設方程的通解為

w(x,t)=(A1e-ikfx+A2eikfx+A3e-ikfx+A4eikfx)eiωt

(3)

式中：A1、A2、A3、A4為由邊界條件、連續條件等確定的待定系數。kf為復波數。若有η<<1,可得如下表達式

(4)

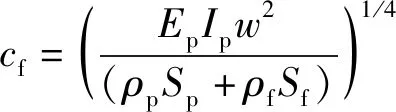
管道的勢能密度和動能密度分別表示為

(5)

(6)

管道的總能量密度為其勢能密度和動能密度之和，因此管道的總能量密度可以表示為

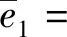
(7)

式中：k1、k2分別表示為復波數kf的實部和虛部，即有關系式，kf=k1+ik2。

Wohlever等[22]已經證明，在高頻計算時，含有A3、A4的近場解可以忽略不計，此時能量密度的平穩遠場解的表達式為

(8)

在管道的振動模型中，彎曲波功率流通常是由剪力和彎矩攜帶傳遞，剪力所對應的功率為

(9)

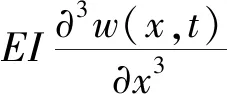
彎矩所對應的功率為

(10)

管道中能量流的平穩解表達式

(11)

比較式(8)和式(11)，可得出遠場能量流與遠場能量密度的梯度成正比關系

無恒產而有恒心者，惟士為能。若民，則無恒產，因無恒心。茍無恒心，放辟邪侈，無不為已。及陷于罪，然后從而刑之，是罔民也。焉有仁人在位罔民而可為也？是故明君制民之產……然后驅而之善，故民之從之也輕。今也制民之產……此惟救死而恐不贍，奚暇治禮義哉？[4](P211)

(12)

式中，cgf=2cf代表彎曲波的群速度。

取一個管道單元進行分析，能量密度隨時間的變化應為管道單元的入射功率與耗散功率之差，可以通過以下表達式[23]得出

(13)

式中：Πin為管道單元的輸入功率；Πdiss為管道單元的耗散功率。

由于結構內的耗散能量與能量密度存在如下的關系式[24]

(14)

聯立式(12)、式(13)、式(14)，不考慮外界輸入的管道單元的能量平衡方程為

(15)

考慮外界輸入則

(16)

1.2 充液管道的能量有限元方程

采用Galerkin加權殘值法對上述方程進行求解，可以得到如下的加權殘值方程表達式[25]

(17)

(18)

為了表述方便，可將式(18)寫成矩陣的形式

[Ke]{ee}={Pe}+{Qe}

(19)

式中:[Ke]表示每個單元含單元剛度和質量的系數矩陣;{ee}則是需要求解的能量密度向量;{Pe}是在節點處輸入的激勵向量;{Qe}表示每個單元兩端能量流的進出。

通過求解式(19)，即可計算得到節點的能量密度，進一步可得到每個管道單元的能量流。

1.3 損傷充液管道的能量有限元計算

當結構中出現損傷后，損傷區域的動力學參數如剛度、阻尼等都會發生變化，從而引起結構中振動能量的變化。因此，基于能量有限元法得到損傷結構的能量流特性和變化特性，從而也可為損傷結構的損傷識別提供依據。

兩種損傷指標都是基于能量有限元法，在后文中將采用能量有限元法對含損傷單元的充液管道的能量密度和能量流進行計算。

2 不同工況下損傷充液管道結構的振動能量分析

2.1 管道結構能量有限元法準確性驗證

在第1節中推導得到了充液管道的能量密度方程和能量有限元方程，為驗證所建立的充液管道能量有限元方程的正確性，本文將能量有限元法(EFEA)解得到的能量密度和傳統有限元(FEA)解的結果進行對比分析。選取一段充液管道，管道兩端固支，管長L為1 m，外徑Ro為10.5 mm，內徑Ri為8 mm，管壁材料密度ρp為7 800 kg/m3，管壁楊氏模量E為210 GPa，阻尼系數η為0.02，管內流體單位長度質量mf為0.2 kg/m，管內流體密度ρf為980 kg/m3。在管道中心處輸入一激勵功率為2.7×10-4W，激勵頻率為8 000 Hz的激勵力。參考能量密度值取為1×10-13J/m。其中，EFEA模型劃分單元數為10，形函數取n=3的Lagrange插值函數，如圖1所示。

有限元模型在ANSYS Workbench中建立，其中FEA模型中模擬管道的三維體單元共58 798個，如圖2所示，流體單元18 706單元，如圖3所示。設置流固耦合屬性，并求解在簡諧激勵下的穩態響應。

圖1 能量有限元模型示意圖Fig.1 Energy finite element model

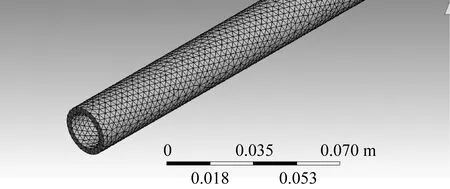
圖2 常規有限元管道單元網格劃分圖Fig.2 FEA grid plot of pipe element

圖3 常規有限元流體單元網格劃分圖Fig.3 FEA grid plot of fluid element

需要注意能量有限元模型和傳統有限元模型的網格劃分原則不同，傳統有限元由于捕捉頻率較高的振動響應時，單元尺寸小，網格規模大。而能量有限元方法求解得到的能量密度是對時間和空間進行平均之后得到的相對平滑的解。因此可將傳統有限元法計算得到的各節點處位移解，按照其本身波長選取合適的長度進行局部平均，得到與能量有限元法計算對應的節點處能量密度值。將兩種方法求得的能量密度進行對比，得到充液管道沿著管道長度方向分布的能量密度圖，如圖4所示。

從圖4中，EFEA得到的各節點能量密度分布與FEA得到的各節點能量密度分布吻合較好，從而驗證了本文建立的充液管道能量有限元方程的正確性。這為后文分析損傷管道的振動特性提供了基礎。

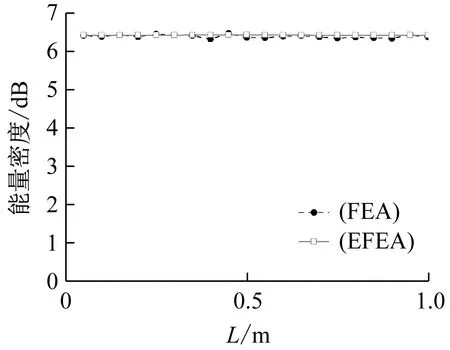
圖4 兩種方法沿管道長度方向能量密度分布的結果對比Fig.4 Energy density distribution along the pipe length

2.2 損傷充液管道的振動分析

2.2.1 損傷單元剛度變化對振動能量的影響

當管道等結構中出現損傷時，其損傷部位的局部剛度一般會減小。在本節中假設損傷僅引起局部剛度減小。

與前述算例類似，將管道分成10個單元，并按管道長度方向進行編號，如圖5所示。其中受損單元編號為6(標深色)，假設該單元損傷后的彈性模量分別降低1%、5%和10%。按照能量有限元法求解損傷前后管道的能量密度和能量流。

圖5 管道的損傷模型Fig.5 Energy finite element model of damaged pipe

當損傷單元的彈性模量降低5%時，圖6給出了能量密度變化的損傷指標Err1沿著長度方向的分布圖。

圖6 管道的損傷指標Err1分布(E=0.95E0)Fig.6 Damage index Err1 distribution (E=0.95E0)

由圖6可知，基于能量密度變化得到的Err1，在受損單元的節點處變化比較明顯，在損傷一側的能量密度變化值會產生突變。這是由于波傳播在經過損傷位置時由于結構不連續出現擾動和不連續的結果，因此可根據管道結構節點的能量密度變化情況來識別管道的損傷位置。

同時也計算出管道中的能量流，從而得到第二種損傷指標并進行分析，如圖7所示。

圖7 管道的損傷指標Err2分布(E=0.95E0)Fig.7 Damage index Err2 distribution (E=0.95E0)

從圖7中看出，Err2在受損6號單元處表現明顯，可以直觀的反映出受損單元，因此可由管道結構的能量流變化情況來識別管道結構的損傷位置。

將損傷單元的彈性模量分別減小1%、5%和10%，結構的損傷采用能量流前后的差值表示，即Δq=|qi-q0|，如圖8所示。

圖8 不同剛度變化情況下管道能量流差值比較Fig.8 Damage index Δq of different stiffness

從圖中可見隨著損傷單元剛度變化幅度的增加，管道單元能量流差值變化也更加明顯，并且都在損傷單元處達到峰值。

2.2.2 損傷單元阻尼變化對振動能量的影響

本算例中假設損傷僅引起局部單元的阻尼增大。假設算例中損傷單元的阻尼分別增大1%、5%，采用能量有限元法計算充液管道的能量密度和能量流。圖9給出了損傷單元阻尼增大1%時，Err2的分布圖。圖10為損傷單元取不同阻尼值時的能量流差值。

圖9 管道的損傷指標Err2 分布(η=1.01η0)Fig.9 Damage index Err2 distribution (η=1.01η0)

從圖9中看出，當某個單元的阻尼發生變化時，會引起周圍能量流明顯的突變，同樣可以清晰地識別出充液管道的損傷部位，從圖10中看出，隨著損傷單元的阻尼增大，損傷前后管道中能量流差值會有明顯的上升。表明損傷引起的阻尼變化越明顯，管道能量流的變化也越明顯，從而可以反映損傷的程度變化。

圖10 不同阻尼變化情況下管道能量流差值比較Fig.10 Damage index Δq of different damping

3 結 論

本文基于能量有限元法對含有損傷的充液管道的振動特性進行了分析。推導得到了充液管道的能量有限元方程。將EFEA的方法同傳統的有限元FEA的結果進行了分析和驗證，表明本文建立的充液管道的能量有限元模型的準確性。

在驗證管道能量有限元方法合理性的基礎上，將其應用于分析損傷管道結構中，通過管道單元的彈性模量的減小和阻尼的增大來模擬結構損傷的程度，利用能量有限元法計算充液管道中單元的能量密度和能量流。通過分別建立基于能量密度和能量流的兩個損傷指標，發現兩種損傷指標都可以表征出損傷位置，其中能量流差值對管道結構的損傷更為敏感。

與傳統的基于振動的損傷識別方法相比，本文提出的方法避開了繁瑣的模態參數求解，且對結構微小的缺陷十分敏感，有一定的優勢。但應用到實際工程中，還需要進一步深入研究。