基于Hertz接觸的單自由度碰振系統的隨機響應近似閉合解
祝海生,陳林聰,孫建橋,趙珧冰
(1.華僑大學 土木工程學院,福建 廈門 361021;2.加州大學Merced分校 工程學院,美國加利福尼亞州 95343;3.天津大學 機械工程學院,天津 300072)
碰撞振動系統普遍存在于工程領域中。由于碰撞振動系統的強非線性,使得關于碰撞振動系統的一些動力學性能研究變得極其復雜,如碰振系統中的隨機響應、分叉以及混沌等。實際的工程領域中的一些碰振現象亦體現了碰撞振動系統產生的影響,如橋梁梁端的碰撞振動導致的梁端開裂;海洋中輪船與冰塊的碰撞振動造成的船體損傷;列車車輪與鐵軌之間的碰撞所造成的一系列的材料、能量消耗。因此,基于碰撞振動現象的普遍性以及在各工程領域產生的影響,對于碰撞振動的研究具有十分重要的實際意義。
碰撞振動是一類非常復雜的動力學過程。根據碰撞過程中所表現的一系列動力學和物理學特征,例如碰撞時物體的相對速度、碰撞接觸時間、碰撞接觸面的形狀變化以及碰撞區域的彈塑性變形等。碰撞振動現象的描述一般主要有兩種模型,分別是瞬時沖擊模型和Hertz接觸理論及其修正模型。目前,基于瞬時沖擊模型,Dimentberg[1-2]就隨機激勵下線性碰撞振動系統的隨機響應分析分別做了大量的研究。王亮等[3]定義了一種隨機響應度量研究了一類二自由度碰撞振動系統在隨機白噪聲激勵下的隨機響應,通過與數值模擬比較討論了隨機噪聲對于系統的影響。田海勇等[4]通過建立一類單自由度含間隙的碰撞振動系統的動力學模型,討論了隨機干擾對碰撞振動系統的影響。伍新等[5]考慮碰撞振動系統的Poincare映射的隱式特點研究了一類三自由度含間隙雙面碰撞振動系統Poincare映射的叉式分岔的反控制問題。Gu等[6]提出了一種預測碰撞系統響應的隨機平均法,利用所提出的隨機平均法考察了高斯白噪聲激勵下的單自由度碰撞振動系統,得到了關于系統能量的平穩概率密度函數。類似的,Liu等[7]討論了碰撞系統在有色噪聲激勵下的平穩概率響應,詳細地討論了有色噪聲和恢復系數對碰撞系統響應的影響。Li等[8]則獲得了相關高斯白噪聲激勵下Duffing-van der Pol碰撞振動系統的平穩概率密度函數,考察了對不同參數引起的隨機分岔問題。徐偉等[9]先借助非光滑變換和狄拉克函數,隨后得到了Duffing-Rayleigh 碰撞振動系統的對應等效非線性系統,最后采用奇異攝動法分析了等效非線性系統的隨機P-分岔。Zhu[10-11]分別將高斯白噪聲和泊松白噪聲激勵下Duffing碰撞振動系統的穩態響應概率密度近似為指數多項式形式。與蒙特卡羅模擬結果進行對比,該指數多項式形式的近似解具有較高的精度,但不能反映系統局部的一些非光滑本質特征。Chen等[12]應用迭代加權殘值法獲得了高斯白噪聲激勵下單自由度碰撞振動系統的穩態響應閉合解。
Hertz接觸理論模型既能夠很好的描述在碰撞過程中的物體的局部變形,同時也能夠較好的反映碰撞過程中的接觸力的變化。在20世紀90年代,Jing等[13-14]基于Hertz接觸理論模型率先獲得了高斯白噪聲外激情形時的單自由度系統的精確平穩解。后來,Huang等[15]利用Hertz理論模型將約束模型轉化為于非線性彈簧,考察了二自由度碰撞振動系統的隨機穩態響應,并在一定條件下得到了這類系統的精確平穩解。Xu等[16-17]聯合利用等效非線性方法和隨機平均法將Hertz模型進行改進分析了單自由度非彈性碰撞振動系統的響應。另外,徐明等[18]采用修正Hertz模型基于隨機平均法分析了在高斯白噪聲激勵下非彈性碰撞振動系統的首次穿越問題,得到了系統的條件可靠性函數和相應的條件概率密度函數。
特別需要指出的是,當前的碰撞隨機振動研究還具有一些局限性。如隨機平均法須在系統恢復系數接近于1以及在弱阻尼弱激勵等情況下才能應用;等效線性化法能夠較為準確的得到系統的均方速度和均方位移,然而其應用范圍卻往往局限于高斯統計的情形,并且在參激情況下常被認為是不充足或不合適的;攝動法只適用于小參數、弱非線性系統條件下,對于非線性較強的情況下的誤差非常大,甚至其結果根本不正確。總之,關于隨機碰撞振動的研究,特別是在隨機響應閉合解方面仍需投入大量的研究。
本文應用隨機振動研究的最新成果——迭代加權殘值法,求解了高斯白噪聲激勵下基于Hertz接觸的單自由度強非線性碰振系統的隨機響應近似閉合解。首先,利用概率環流和概率勢流的概念,構造系統對應簡化FPK方程解的近似表達式;然后,運用加權殘值法獲得系統平穩概率密度函數的近似閉合解;最后,應用迭代的辦法,提高近似閉合解的精度。研究結果表明,本文的迭代加權殘值法采用分段函數形式表達,具有較高的精度,可以有效的解決非光滑問題,同時還清楚的表征了碰振系統的非光滑本質特征等等。作為算例,分別研究Duffing碰振系統和干摩擦碰振系統,來驗證本文方法的有效性。
1 問題概述
考慮一個受高斯白噪聲激勵的單自由度Hertz碰振系統,其圖示和運動方程如圖1所示。

圖1 碰撞振動模型Fig.1 Vibro-impact system

(1)
式中,g1(X,Y)表示線性或非線性阻尼系數,g2(X)表示系統非碰撞回復力,f(X)表示碰撞回復力,其表達式為
(2)
式中,系統平衡點與兩側彈性壁的相互作用規律滿足Hertz接觸定律,δr和δl是碰撞振動系統平衡點距兩端碰撞壁的距離,Br和Bl是常數,其與彈性壁的材料及幾何形狀有關;hi(X,Y)表示線性或非線性激勵幅值,Wi(t)表示高斯白噪聲,其相關函數為E[Wi(t)Wj(t+τ)] =2Dijδ(τ),i,j=1,2,…,l。
與系統(1)相對應的簡化FPK方程如下
(3)
式中,p=p(x,y)為式(1)的平穩概率密度函數;漂移系數(m1,m2)和擴散系數(b22)如下
m1=y
m2=g1(x,y)y+g2(x)+f(x)-
(4)
根據詳細平衡法[19-20],式(3)可分為以下兩個部分
(5)
和
(6)
其中式(5)描述了概率環流的平衡,表示保守系統的能量守恒。式(6)則表明了概率勢流的平衡,表示為系統能量輸入與耗散之間的平衡。可見,詳細平衡法具有明確的物理意義。若系統存在精確平穩解,式(5)和式(6)必同時被滿足。然而,在實際工程中,該情形常難以實現。因此用詳細平衡法求解FPK方程的精確平穩解的能力和范圍是有限的。
迭代加權殘值法[21]是近期作者提出來的一種求解FPK方程平穩解的有效方法。當系統存在精確解時,近似閉合解收斂于精確解。當系統不存在精確解,獲得具有較高精度的近似閉合解。本文將推廣該方法求解簡化FPK方程(3)。
2 迭代加權殘值法
迭代加權殘值法主要由加權殘值法和迭代步驟組成。在具體的應用過程中,先結合概率勢流和概率環流概念,構造簡化FPK方程 (3)的近似表達式;再用加權殘值法獲得近似閉合解;最后引入迭代技術來提高近似閉合解的精度。
2.1 加權殘值法
首先,假定方程(3)的平穩解是如下形式
(7)
式中,C0是歸一化常數,φ(x,y)關于狀態變量的多項式,按照文獻[21]可由以下形式三部分組成

k2ψ2(x,y)
(8)
式中,cij,k1,k2是待求系數,ψ1和ψ2是概率勢流和概率環流,分別滿足式(5)與(6),表達式如下
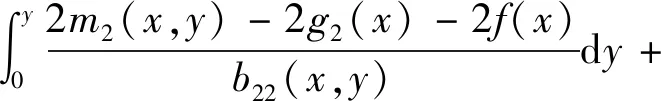
lnb22(x,y)
(9)

φ(x,y)→∞ asA→∞,α>-1
ifφ(x,y)∝AαasA→0
(10)
式中,x=Asinθ,y=Acosθ,其中第二個條件保證了在原點的可積性。


(11)

(12)
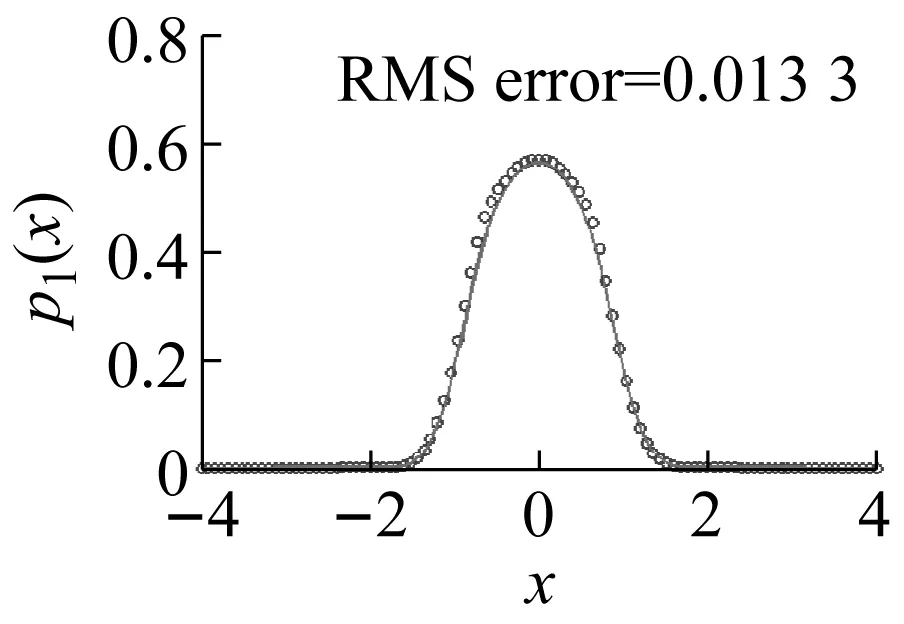
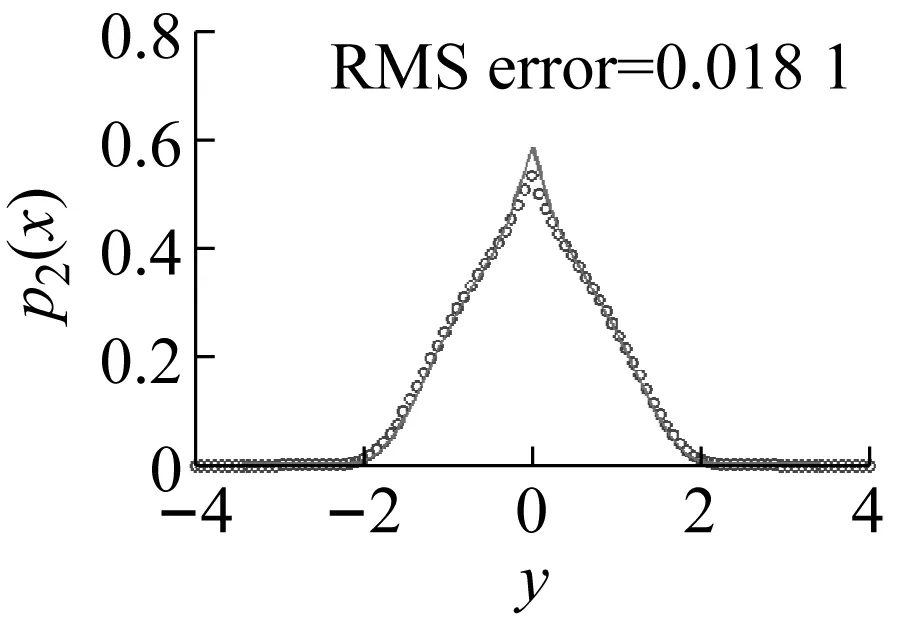
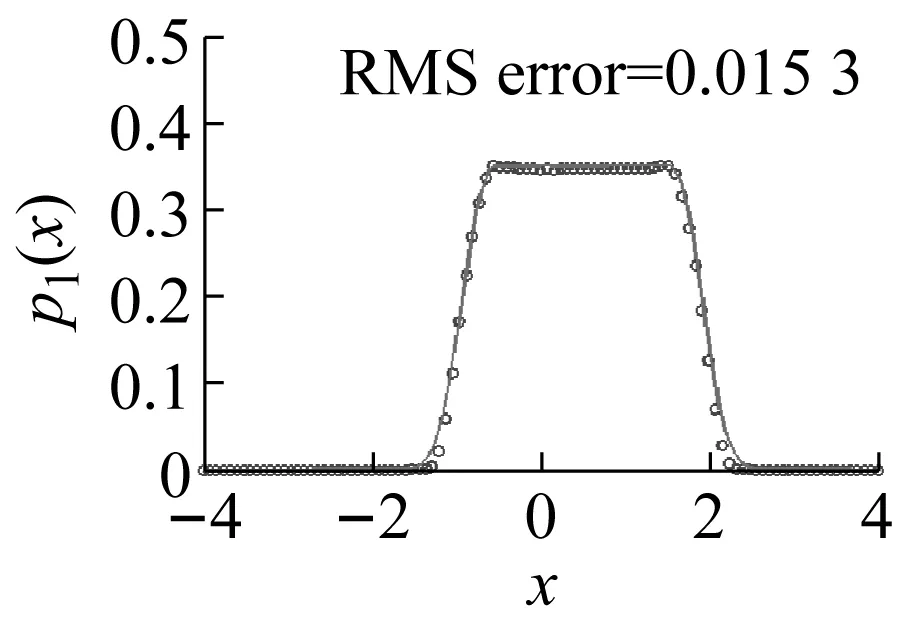
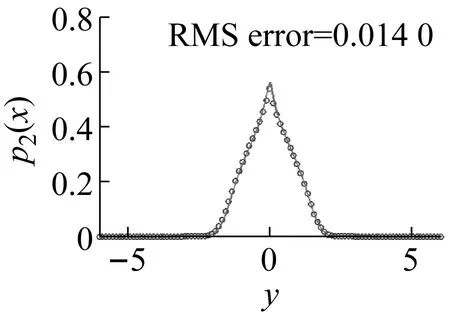
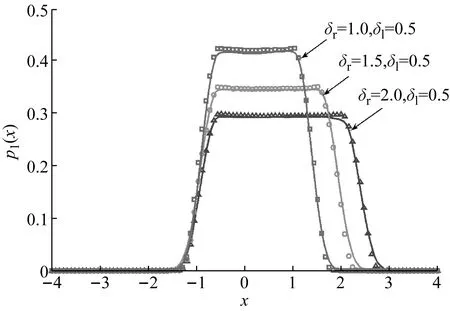
式中,Ml(x,y)(l=1,2,…,N+2,0 Mk(x,y)=pm(x,y)xiyj,k=1,2,…,N MN+1(x,y)=pm(x,y)ψ1(x,y) MN+2(x,y)=pm(x,y)ψ2(x,y) (13) 式中,pm可為由等效線性化獲得的高斯概率分布函數或隨機平均法獲得的概率分布函數,也可構造為如下形式的函數 pm(x,y)=exp[-ψ1(x,y)-ψ2(x,y)] (14) (15) 為了評價近似解的精度,將近似解與參考解pR(x,y)之間的均方誤差的平方根定義為 (16) 式中,pR=pR(x,y)可以是蒙特卡羅模擬結果,也可以是精確解析解。 需指出的是,迭代方向的選擇也是至關重要的。若迭代方向選取的不好,可能會獲得一個不收斂的結果。這一現象在一些強非線性系統當中表現的尤為突出。因此,Chen等[23]提出了一種漸近迭代的概念,具體步驟是先應用加權殘值法計算弱非線性系統或弱激勵情形時的近似平穩概率密度函數,然后以此構造權函數,再在非線性參數空間里,逐步搜索強非線性系統的近似平穩概率密度函數。 (17) 接下來,我們將分別考察兩個算例,說明迭代加權殘值法在Hertz碰撞隨機振動系統研究中的適用性。 考慮在高斯白噪聲激勵下的Duffing碰撞隨機振動系統,運動方程如下 (18) 式中,β1>0,Wi(t)表示激勵強度為2Di的獨立的高斯白噪聲。 對應FPK方程的漂移系數和擴散系數如下 (19) 由此可得出概率勢流和概率環流為以下形式 (20) 下面分別考察了對稱情形與非對稱情形。 對稱情形:設δr=δl=0.5,β1=0.1,D1=0.1,α1=1,α3=0.5,Br=Bl=10,經2次迭代之后所得結果如下 p(x,y)=0.228 791 97×exp[-0.942 889 34x2+ 0.007 802 02xy+0.180 384 93y2- 0.075 531 07x4+0.0008 465 5x3y- 0.196 890 08x2y2-0.002 027 02xy3- 0.378 371 96× (21) 根據式(16),式(21)的精度為0.013 3。 圖2給出了系統(18)在Br=Bl=10,δr=δl=0.5對稱情形時的平穩響應概率密度函數。其中圖2(a)與(b)分別表示其聯合概率密度函數的理論近似閉合解(21)與相應的蒙特卡羅模擬結果(樣本數為108);圖2(c)與(d)分別表示關于位移的邊緣概率密度函數與關于速度的邊緣概率密度函數,其中實線表示解析結果,符號(○)表示蒙特卡羅模擬結果。如圖所示,迭代加權殘值法計算的結果與蒙特卡羅模擬結果非常相近,精度令人滿意;系統平穩響應概率密度函數是單峰態,且頂部光滑;初步表明了本文方法在Duffing系統對稱情形中是有效的。 (a) (b) (c) (d)圖2 系統(18)在Br=Bl=10,δr=δl=0.5情形時的平穩概率密度函數Fig.2 The stationary PDF of system (18)in the case of Br=Bl=10 and δr=δl=0.5 非對稱情形:為了進一步考察迭代加權殘值的有效性和精度,現以平穩響應概率密度函數(21)構造權函數,應用迭代加權殘值法分別考慮不同彈性壁剛度Br(Bl)與不同碰撞壁間距參數δr(δl)等非對稱情形下的平穩響應概率密度函數的分布。 首先,針對不同彈性壁剛度Br(Bl)情形,現選取Br=100,Bl=10。經3次迭代得到精度為0.020 5的結果如下 p(x,y)=0.262 593 24×exp[0.101 677 44x- 0.002 757 12y-0.914 625 26x2+ 0.008 178 59xy+0.055 220 25y2- 0.736 233 78x3+0.000 004 81x2y- 0.007 625 82xy2+0.006 756 1y3- 0.494 431 02x4-0.003 171 1x3y- 0.167 376 57x2y2-0.002 123 55xy3- 0.497 403 68× (22) 類似地,圖3給出了系統(18)在Br=100,Bl=10情形時的平穩響應概率密度函數。由圖3可知,迭代加權殘值法計算結果依然能夠吻合的很好;系統平穩響應概率密度函數整體呈光滑“竹筍”狀,關于位移的邊緣概率密度具有顯著的非對稱性;迭代加權殘值法進一步得到了有效驗證。另外,由圖2和圖3可以得出,系統關于速度的邊緣概率密度函數函數基本相同。 現結合對稱情形,并增加計算Br=20,Bl=10這一情況(受篇幅所限,不再贅述具體表達式,下同),考慮系統在一側彈性壁剛度不同的情形下對于位移的邊緣概率密度函數的影響情況。由下圖4可知,隨著彈性壁剛度Br(Bl)的增大,關于位移的邊緣概率密度函數峰值會變大,系統穩態響應會有所減小。 (a) (b) (c) (d)圖3 系統(18)在Br=100,Bl=10情形時的平穩響應概率密度函數,其他參數同圖2Fig.3 The stationary PDF of system (18)in the case of Br=100,Bl=10.The other parameters are the same as those in Fig.2 圖4 系統(18)分別在Br=Bl=10、Br=20,Bl=10以及Br=100,Bl=10時關于位移邊緣概率密度函數,其中實線表示理論解析解,符號(o,△,□ )表示蒙特卡羅模擬結果,其他參數同圖2Fig.3 The marginal PDF of displacement of system (18)in the cases of Br=Bl=10,Br=20,Bl=10 or Br=100,Bl=10,respectively.Solid line represents the analytical solution,symbols(o,△,□ )represent the Monte Carlo simulation data.The other parameters are the same as those in Fig.2 然后固定參數Br(Bl),考察不同碰撞壁間距參數δr(δl)情形,現選取δr=1,δl=0.5,Br=Bl=10,經4次迭代得到精度為0.025 1的結果如下 p(x,y)=0.195 716 30×exp[-0.058 343 74x+ 0.002 590 17y-0.677 146 06x2+ 0.010 489 24xy+0.200 581 69y2+ 0.181 499 36x3+0.000 701 53x2y+ 0.012 265 64xy2-0.000 749 63y3- 0.123 542 70x4+0.000 511 15x3y- 0.330 673 92× 0.167 784 26x2y2-0.002 800 01xy3- (23) 由圖5可知,在不同碰撞壁間距參數下應用迭代加權殘值法計算的結果與樣本數為108的蒙特卡羅模擬結果吻合的效果也能夠令人滿意,關于位移的邊緣概率密度數也具有較明顯的非對稱性。類似于圖4,圖6討論了系統平衡點到碰撞壁一側間距增大時關于位移邊緣概率密度函數的分布情況。由圖6可知,隨著系統平衡點到碰撞壁一側間距增大時,系統的“單峰”單側坡度會有所變緩,系統的穩態響應會增大。 算例1研究表明,迭代加權殘值法在光滑Hertz碰振系統研究中可取得較好的效果。下面將考察一類非光滑系統Hertz碰撞系統,來進一步檢驗迭代加權殘值法的適用性。現以干摩擦碰振系統為例,其運動方程如下 (a) (b) (c) (d)圖5 系統(18)在δr=1,δl=0.5時的平穩概率密度函數,其他參數同圖2Fig.5 The stationary PDF of system (18)in the case of δr=1,δl=0.5.The other parameters are the same as those in Fig.2 圖6 系統(18)在δr=δl=0.5,δr=1,δl=0.5與δr=2.5,δl=0.5時關于位移邊緣概率密度函數。其中實線表示理論解析解,(o,△,□ )表示蒙特卡羅模擬結果,其他參數同圖2Fig.6 The marginal PDF of displacement of system (18)in the cases of δr=δl=0.5,δr=1,δl=0.5 or δr=2.5,δl=0.5,respectively.The solid line represents the analytical solution,symbols (o,△,□ )represent the Monte Carlo simulation data.The other parameters are the same as those in Fig.2 (24) β0,β1,β3≥0,sgn(Y)為符號函數,W(t)表示激勵強度為2D1的高斯白噪聲。系統的平穩FPK方程形如式(3),對應的漂移系數和擴散系數如下 b22=2D1 (25) 相應概率勢流和概率環流如下形式 (26) 同樣,針對干摩擦系統亦考慮對稱情形與非對稱情形。 對稱情形:取參數:δr=δl=0.5,Br=Bl=5,β0=β1=β3=0.1,D1=0.1。應用迭代加權殘值法經過3次迭代計算得到精度為0.018 1的結果如下 p(x,y)=0.280 673 82×exp[0.049 948 83x2- 0.009 358 99xy+0.463 128 39y2- 0.191 118 95x4+0.007 645 05x3y+ 0.018 861 58x2y2+0.012 918 00xy3- 1.087 645 1× 0.262 478 15y4-1.082 915 1|y|] (27) 圖7為系統(24)在Br=Bl=5對稱情形時的平穩響應概率密度函數結果。圖7(a)與(b)分別表示基于式(27)的聯合穩態概率密度函數與相應的蒙特卡羅模擬結果(樣本數為108)。圖7(c)與(d)分別表示關于位移的邊緣概率密度函數與關于速度的邊緣概率密度函數。由圖7可知,理論解析結果與蒙特卡羅模擬結果非常相近;系統平穩響應概率密度函數是單峰,頂部呈“刀鋒”狀,充分體現出了干摩擦系統的非光滑特征。 (a) (b) (c) (d)圖7 系統(24)在Br=Bl=5時的平穩響應概率密度函數Fig.7 The stationary PDF of system (24)in the symmetry case of Br=Bl=5 接著,以式(27)構造權函數,經3次迭代,求得了Br=Bl=10情形下精度為0.020 3的平穩響應聯合概率密度函數,其表達式如下 p(x,y)=0.319 755 06×exp[0.145 562 56x2- 0.014 088 440xy+0.464 592 29y2- 0.509 706 45x4+0.016 608 98x3y+ 0.032 655 97x2y2+0.014 236 69xy3- 0.992 554 01× 0.272 600 96y4-1.097 960 4|y|] (28) 根據式(28)以及蒙特卡羅模擬結果得出了系統在Br=Bl=10情形時的平穩響應概率密度函數,如圖8所示。由圖8可知,與Br=Bl=5情形相比,Br=Bl=10情形時系統“刀鋒”的開口寬度有所減小;系統的干摩擦特征仍獲得了比較好的體現。此外,比較圖7和圖8(以及下圖10和圖11)也可以得出,系統在所研究的情形下關于速度的邊緣概率密度函數也幾乎相同。 為了考察不同彈性壁剛度Br(Bl)對系統響應的影響,我們也考察了Br=Bl=20這一情況。圖9給出了不同彈性壁剛度情形下關于位移的邊緣概率密度函數對比圖。由圖9知,當系統彈性壁剛度逐漸增大時,系統的“刀鋒”開口寬度是逐漸減小的,系統的穩態響應也在減小;另外,初步得出系統的“刀鋒”寬度與系統的彈性壁剛度大小是無關的。 由以上可知,應用迭代加權殘值法在干摩擦系統對稱情形中,當彈性壁剛度逐步增大時,仍然能夠保持較高的精度,初步表明了本文方法在干摩擦碰撞振動系統對稱情形中的有效性和適用性。 (a) (b) (c) (d)圖8 系統(24)在Br=Bl=10時的平穩概率密度函數,其他參數與圖7相同Fig.8 The stationary PDF of system (24)in the case of Br=Bl=10.The other parameters are the same as those in Fig.7 圖9 系統(24)分別在Br=Bl=5、Br=Bl=10與Br=Bl=20時關于位移的邊緣概率密度函數。其中實線表示理論解析解,(o,△,□ )表示蒙特卡羅模擬結果Fig.9 The marginal PDF of displacement of system (24)in the cases of Br=Bl=5,Br=Bl=10 and Br=Bl=20,respectively.The solid line represents the analytical solution,symbols(o,△,□ )represent the Monte Carlo simulation data 非對稱情形:現固定參數Br=Bl=10,考察不同碰撞壁間距參數δr(δl)情形。先取δr=1.5,δl=0.5,β0=β1=β3=0.1,D1=0.1。以式(28)構造權函數,經3次迭代之后得出精度為0.015 3的結果。表達式如下: p(x,y)=0.192 588 83×exp[-0.000 033 18x+ 0.000 439 14y+0.001 236 61x2- 0.001 225 29xy+0.493 140 42y2+ 0.000 024 08x3+0.000 068 03x2y- 0.000 062 91xy2-0.000 213 25y3- 0.000 912 73x2y2+0.002 382 99xy3- 1.256 498 2× 0.000 074 00x4+0.000 030 95x3y- 0.250 424 29y4-1.013 793 0|y|] (29) 圖10進一步給出了δr=1.5,δl=0.5非對稱情形時的平穩響應概率密度函數。由圖10可知,關于位移的邊緣概率密度函數亦表現出明顯的非對稱性,系統平穩響應概率密度函數的峰值區間基本維持在1.5~-0.5;另外,迭代加權殘值法計算的結果與樣本數為108的蒙特卡羅模擬結果吻合的也非常好,干摩擦的非光滑性也得到了充分體現。 現保持δl不變,取δr=2。以式(29)構造權函數,經2次迭代獲得精度為0.014 0的平穩響應聯合概率密度函數閉合解如下 (a) (b) (c) (d)圖10 系統(24)在δr=1.5,δl=0.5時的平穩概率密度函數Fig.10 The stationary PDF of system (24)in the case of δr=1.5,δl=0.5 p(x,y)=0.163 760 83×exp[-0.010 293 78x- 0.006 261 64y+0.027 450 11x2- 0.001 538 97xy+0.492 225 00y2+ 0.002 910 81x3+0.000 761 82x2y+ 0.010 068 95xy2+0.005 455 80y3- 0.005 365 30x4-0.001 042 16x3y- 0.022 606 36x2y2+0.003 372 81xy3- 1.354 765 5× 0.250 615 05y4-1.018 964 6|y|] (30) 圖11給出了系統在δr=2.0,δl=0.5情形時的平穩響應概率密度函數。此時由于δr的增大,系統平穩響應概率密度函數的峰值區間也基本保持在2.0~-0.5;結合圖10和圖11可以發現,系統的“刀鋒”開口寬度隨著碰撞壁間距(δr)的增大有所增大。圖12給出了δr=1.0,δl=0.5、δr=1.5,δl=0.5與δr=2,δl=0.5情形時關于位移的邊緣概率密度函數對比圖,考察了不同碰撞壁間距系數δr(δl)對系統響應的影響。由圖12可知,所舉三種情況下的平穩響應邊緣概率密度函數峰值區間基本都維持在x=δr和x=δl之間,再結合圖9和圖12可以得出,系統的“刀鋒”的區間寬度只與δr(δl)有關,與Br(Bl)無關;另外,邊緣概率密度函數p1(x)峰值分別在0.42、0.35和0.3左右,比較三種情況得知,當系統平衡點到碰撞壁一側間距增大時,關于位移的邊緣概率密度的“刀鋒”峰值會有所降低,同時“刀鋒”開口寬度會有所增大;研究表明應用迭代加權殘值法在干摩擦碰撞振動系統的研究中也是有效的。 (a) (b) (c) (d)圖11 系統(24)在δr=2,δl=0.5時的平穩概率密度函數,其他參數同圖10Fig.11 The stationary PDF of system (24)in the case of δr=2,δl=0.5.The other parameters are the same as those in Fig.10 圖12 系統(24)分別在δr=1.0,δl=0.5、δr=1.5,δl=0.5與δr=2,δl=0.5時關于位移的邊緣概率密度函數。其中實線表示理論解析解,符號(o,△,□ )表示蒙特卡羅模擬結果。其他參數同圖10Fig.12 The marginal PDF of displacement of system (24)in the cases with δr=1.0,δl=0.5、δr=1.5,δl=0.5 or δr=2,δl=0.5,respectively.The solid line represents the analytical solution,symbols(o,△,()represent the Monte Carlo simulation data.The other parameters are the same as those in Fig.10 本文采用迭代加權殘值法研究了隨機激勵下基于Hertz接觸的單自由度強非線性碰撞振動系統平穩響應問題。研究方法主要有三個步驟:首先構造支配系統平穩響應概率密度函數的簡化FPK方程的近似表達式;然后,應用加權殘值法獲得系統平穩概率密度函數的近似閉合解;最后應用迭代技術,來提高近似閉合解的精度。作為算例,分別研究了Duffing碰振系統以及干摩擦碰振系統。研究表明本文的方法在光滑系統(Duffing碰振系統)以及非光滑系統(干摩擦碰振系統)研究中均是有效和適用的,同時還完全表征了系統的非線性動力學特征,如干摩擦系統頂部的“刀鋒”非光滑特征。
2.2 迭代過程


3 算 例
3.1 算例1




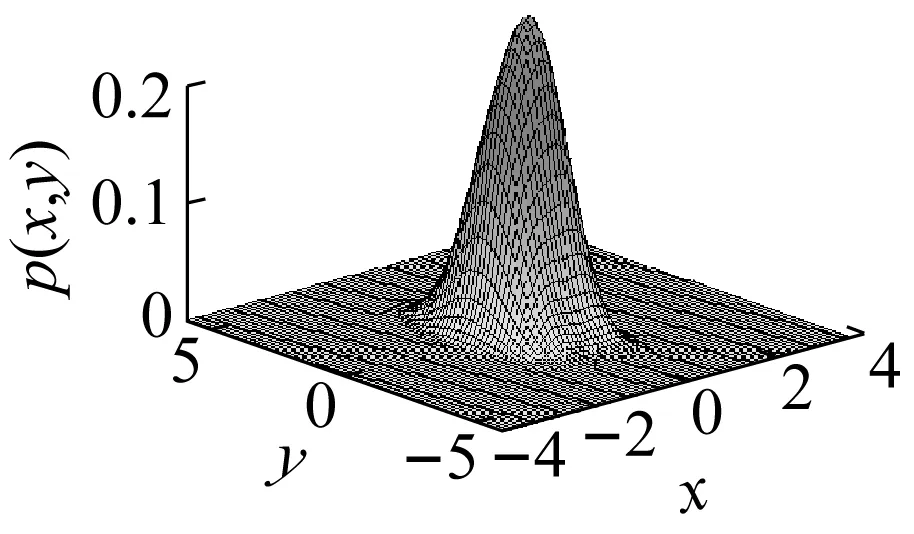




3.2 算例2





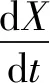














4 結 論

