基于復相關系數的時滯聯合估計及其應用

李海軍　夏靜　史恒惠　劉長良　王梓齊

摘要：針對工業過程的軟測量建模，為對輸入與輸出變量間的時滯關系進行準確、快速地估計，提出一種基于復相關系數的時滯聯合估計方法。該方法以模型輸入和輸出數據間的復相關系數為指標，將時滯聯合估計問題轉化為多維優化問題，進而對各輸入變量的時滯時間進行尋優。針對火電廠脫硝系統的NO，排放軟測量，基于實際的運行數據和最小二乘支持向量機算法，對所提出的方法進行驗證并與其他時滯估計方法進行對比。結果表明：基于復相關系數的時滯估計方法計算速度較快，時滯估計結果較準確，能在一定程度上提高軟測量模型的準確度。

關鍵詞：復相關系數;時滯聯合估計;NO_x排放;軟測量

中圖分類號：TP206 文獻標志碼：A 文章編號：1674-5124（2019）08-0140-05

收稿日期：2018-07-16;收到修改稿日期：2018-09-04

基金項目：北京市自然科學基金資助項目（4182061）

作者簡介：李海軍（1973-），男，河南焦作市人，工程師，研究方向為火電機組軟測量、遠程診斷。

0 引言

工業過程的軟測量建模，除了受輔助變量選取、建模方法等因素的決定外，輔助變量與主導變量間的時滯關系同樣會對模型準確度產生一定的影響[1]。若不考慮輔助變量的時滯，會在一定程度上對模型的準確度產生負面影響。對于復雜的生產過程，很難通過機理分析確定具體的時滯時間。因此，在實際應用中多采用數據驅動方法估計輔助變量的時滯時間，主要分為單變量估計和聯合估計兩種。

單變量估計獨立地分析每個輔助變量與輸出變量間的時滯關系，有著便于實現、計算速度快等優點。文獻[2]基于相關系數確定時間序列模型中的最優時滯因子并應用于交通流量的預測。文獻[3]基于歸一化互信息確定聚丙烯熔融指數預測模型中各自變量的時滯時間。文獻[4]提出了一種基于模糊曲線分析的單變量時滯估計方法。文獻[5]將模糊曲線分析時滯估計與選擇性集成高斯過程回歸算法進行結合，建立了脫丁烷塔底濃度的軟測量模型。但是，單變量估計在計算時中忽略了其他輔助變量對輸出的影響以及輔助變量之間的相互影響，有可能會導致估計結果的不準確。

聯合估計綜合考慮各輔助變量與輸出間以及各輔助變量之間的關系從而確定時滯時間。文獻[6]以所有輔助變量和主導變量間的聯合互信息作為目標函數對時滯時間進行尋優。文獻[7]以軟測量模型的訓練誤差作為目標函數，使用混合差分進化算法對時滯時間進行尋優。文獻[8]使用差分進化算法對時滯時間進行尋優，并結合偏最小二乘算法，建立了常壓塔干點的軟測量模型。但是，由于需要計算聯合互信息等復雜函數或需要對模型進行訓練，時滯聯合估計在輸入維數高、樣本數量大的情況下往往運算時間較長，不利于實際的工程實踐。

復相關系數是反映一個因變量與一組自變量之間相關程度的指標[9]，其常應用于多元相關分析、多元線性回歸的評價等數理統計領域，文獻[10-11]將復相關系數應用于確定數據包絡分析中自變量與因變量間的時間滯后關系。復相關系數是通過對輸入、輸出數據進行線性擬合進而計算得到的，相比于聯合互信息或訓練數據驅動模型，其計算速度有明顯的優勢。

因此，本文提出了一種基于復相關系數的時滯聯合估計方法。該方法以輔助變量和輸出變量間的復相關系數為指標，將時滯估計轉化為多維優化問題進行求解，有著計算快、準確度高的特點。以火電廠脫硝系統NO_x排放濃度的軟測量為例，基于實際運行數據對所提出方法進行了驗證。

1 基于復相關系數的時滯聯合估計

1.1 過程變量的時滯估計

傳統的軟測量建模中往往不考慮輔助變量的時滯問題，多直接使用同一采樣時刻的輔助變量和輸出變量數據建立模型。但對于工業過程特別是化工、冶煉、發電等相關領域，從工藝流程到測量儀表等環節均存在較大的時滯。因此，有必要在建模過程中考慮各輔助變量的時滯，從而進一步提高軟測量模型的準確度。

考慮輔助變量時滯的軟測量模型結構如下：

y（t）=f[x₁（t-τ₁），x₂（t-τ₂），…，x_n（t-τ_n）]（1）式中：y（t）——軟測量模型的輸出變量;

x_k（t-τ_k）——模型的輔助變量;

τ_k——輔助變量x_k的時滯時間。

輔助變量的時滯估計是采用機理分析或數據驅動方法，計算輔助變量的時滯時間τ。對于復雜的工業過程，很難使用機理分析方法精確計算各輸入變量的時滯時間，常用數據驅動方法進行時滯估計。

數據驅動時滯估計方法的基本思想是將同一采樣時刻的歷史輸入數據X（t）∈Rⁿ進行時序重構，得到新的輸入數據X_d（t）=[X₁（t-τ₁），X₂（t-τ₂），…，X_n（t-τ_n）]^T。

之后基于某一給定的指標（如互信息、相關系數等）確定最優的時滯時間。數據驅動時滯估計方法主要分為單變量估計和聯合估計兩種。

單變量時滯估計獨立地分析單個輔助變量與輸出間的時滯關系，即將時滯估計問題轉化為如下的優化問題：其中，f₁可為相關系數、互信息等目標函數。

單變量時滯估計通過數個一維優化問題進行求解，計算速度相對較快。但在尋優時僅考慮某個輔助變量與輸出的關系而忽略了其他輔助變量與輸出的關系以及輔助變量之間的關系，存在一定的片面性，可能會在一定程度上導致估計結果的不準確，從而影響軟測量模型的準確度。

時滯聯合估計方法綜合考慮各輔助變量與輸出以及各輔助變量之間的關系，對各輔助變量的時滯時間進行聯合尋優，即轉化為如下的優化問題：其中，f₂可為聯合互信息、軟測量模型訓練誤差等目標函數。

時滯聯合估計通過多維優化問題進行求解，相比于單變量估計從理論上更為準確。但是，聯合估計在尋優過程中需要計算聯合互信息等復雜函數或需要對軟測量模型進行訓練，在輸入維數高、樣本數量大的情況下耗時較長，不利于工程實踐。

1.2 復相關系數及其在時滯估計中的應用

復相關系數R越大，表明因變量和該組自變量間的線性相關程度越大。復相關系數R通常使用以下步驟進行計算：

1）使用時序重構后的輸入數據X_d（t）和輸出數據Y（t）進行多元線性回歸。

2）基于線性模型計算預測諽Y（t）。

3）計算實際值Y（t）和預測值Y（t）之間的簡單相關系數，即為Y（t）和X_d（t）間的復相關系數R，具體的計算公式如下：其中，Y為實際值Y（t）的算術平均值。

除上述步驟外，復相關系數R也可以通過X_d（t）和Y（t）多元線性回歸后得到的決定系數R²開方得到。

基于復相關系數進行時滯聯合估計，即求解如下規劃問題：其中，由于時滯時間應為采樣間隔的整數倍，故其定義域應為自然數域N;T為時滯時間的上界。

上述規劃問題是非線性整數規劃問題，可采用分支定界法或啟發式算法進行求解。啟發式算法的結構較為簡單、計算速度較快，但無法方便處理復雜的約束條件。由于以上規劃問題不含等式、非線性等復雜的約束條件，可使用啟發式算法進行求解。

相比于單變量時滯估計，復相關系數在計算時充分考慮了自變量間的相關關系，估計結果相對更為準確;相比于其他時滯聯合估計方法，進行多元線性回歸所需要的時間要遠小于計算聯合互信息或訓練軟測量模型，實時性相對較好。因此，從理論上講，基于復相關系數的時滯聯合估計能夠更好地平衡估計結果的準確性和計算的快速性。

2 復相關系數時滯聯合估計在軟測量中的應用

2.1 火電廠脫硝系統及NO_x排放軟測量

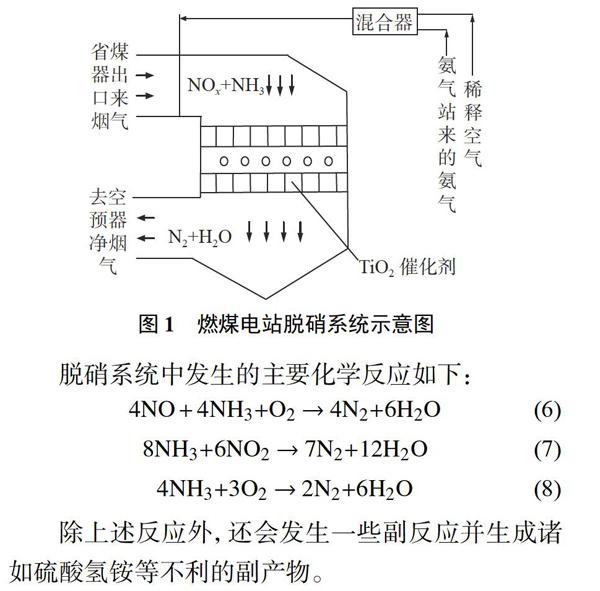
圖1為火電廠脫硝系統工藝流程的示意圖。脫硝系統布置在鍋爐的省煤器與空預器之間，其基本工作過程如下[12]：氨氣與風機送來的空氣進行混合后通過噴嘴進入煙道，與省煤器出口來的煙氣充分混合后進入反應器，在催化劑的催化作用下發生還原反應，將煙氣中的NO_x還原為氮氣與水蒸氣。

脫硝系統中發生的主要化學反應如下：

4NO+4NH₃+O₂→4N₂+6H₂O（6）

8NH₃+6NO₂→7N₂+12H₂O（7）

4NH₃+3O₂→22+6H₂O（8）

除上述反應外，還會發生一些副反應并生成諸如硫酸氫銨等不利的副產物。

由于脫硝系統中氣體分析儀表的測量滯后較大且需要頻繁進行吹掃，導致傳統的控制策略往往難以長時間精確地控制噴氨量。噴氨量偏少會導致NO_x排放超標，而過量噴氨除了會導致經濟上的損失外，還會造成催化劑壽命縮短、下游設備堵塞、氨逃逸率增大等不良后果。因此，有必要建立準確的NO_x排放濃度軟測量模型以進一步實現噴氨量的閉環優化控制。

一般情況下，考慮輔助變量時滯估計的軟測量建模步驟如下：

1）根據過程機理以及現場實際測點情況，確定與輸出變量密切相關的輔助變量。

₂）獲取相應的運行數據并進行去離群點、濾波、歸一化等預處理操作，之后確定軟測量模型的訓練樣本和測試樣本。

3）基于訓練樣本以及相應的時滯估計方法，確定各輔助變量的時滯時間并對訓練、測試樣本進行時序重構。

4）基于選定的軟測量建模方法，使用時序重構后的訓練、測試樣本對軟測量模型進行訓練和測試。

2.2 輔助變量選取及數據預處理

結合2.1中的機理分析及數據庫中實際的測點情況，同時考慮機組負荷變化對脫硝過程產生的影響，選擇脫硝系統入口 NO_x濃度、入口煙氣含氧量、出口煙氣含氧量、煙氣流量、入口煙氣溫度、噴氨量和機組負荷共7個變量作為軟測量模型的輔助變量，輸出變量為脫硝系統出口的NO_x濃度。

從數據庫中導出一段變負荷工況下的運行數據，采樣間隔為10s，共1200組。基于拉依達準則剔除離群點，之后基于滑動窗口法進行濾波。剩余1067組數據并從中選取1000組數據進行歸一化后參與軟測量建模，選擇前800組數據作為訓練樣本，后200組數據作為測試樣本。歸一化前建模數據中各變量的變化范圍如表1所示。

2.3 基于復相關系數的輔助變量時滯估計

考慮到脫硝系統中氣體分析儀表的響應時間一般為30～120s，故設定各輔助變量時滯時間的上界T=120s。為對比各時滯估計方法在估計結果上的不同，同時基于復相關系數法、相關系數法和聯合互信息法對7個輔助變量進行時滯估計。相關系數法使用枚舉法進行求解，復相關系數法和聯合互信息法均用遺傳算法求解。遺傳算法的種群規模設置為20，迭代次數為100。

各方法時滯估計的結果如表2所示。相關系數法計算耗時0.05s，復相關系數法耗時1.%s，聯合互信息法耗時51.46s。

從表中可以看出，復相關系數法和聯合互信息法的時滯估計結果較為接近，而與相關系數法存在一定的差異。從機理上分析，入口NO_x濃度和煙氣含氧量這兩個測點均位于脫硝系統的入口處且使用同一氣體分析儀表進行測量，其與輸出變量的時滯關系應基本一致;而出口煙氣含氧量和出口NO_x濃度的測點位置和測量儀表均相同，兩者間應不存在時滯關系。因此，復相關系數法和聯合互信息法的估計結果要比相關系數法更具有準確性。同時結合3種算法的計算時間，相比于相關系數法和聯合互信息法，復相關系數法時滯估計的準確性和計算速度均較快，有著一定的優勢。

3 實驗結果及分析

火電廠的NO_x排放濃度常用人工神經網絡[13]、最小二乘支持向量機[14]等智能方法建立軟測量模型。相比于人工神經網絡等機器學習方法，最小二乘支持向量機（least square support vector machine，LS-SVM）有著泛化能力較強、能夠收斂至全局最優點、訓練速度較快的優點。因此，本文選擇LS-SVM算法建立NO_x排放的軟測量模型。

LS-SVM的實現基于Matlab的LS-SVM工具箱，選擇LS-SVM的核函數為線性函數，參數訓練選擇貫序最小優化（sequentialminimal optimization，SMO）算法。基于LS-SVM分別建立不進行輔助變量時滯估計和使用復相關系數法進行時滯估計兩種情況下的NO_x排放軟測量模型。兩個模型預測值與實際值的對比以及預測殘差間的對比如圖2和圖3所示。

如圖2和圖3所示，使用復相關系數進行時滯估計后，軟測量模型的準確度和跟蹤能力均要顯著優于無時滯估計的模型，說明引入輔助變量的時滯信息能有效提高軟測量模型的準確度。

為了比較各時滯估計方法對模型準確度的影響，分別基于相關系數法和聯合互信息法的時滯估計結果建立軟測量模型，并在測試樣本上與不進行時滯估計和復相關系數法進行比較，結果如表3所示。其中RMSE為模型在測試樣本上的均方根誤差， MRE為模型在測試樣本上的平均相對誤差。

由表可知，進行輔助變量時滯估計后，模型的準確度都有著一定程度的提高，而相關系數法準確度提高的程度要小于聯合互信息法和復相關系數法，與1.1中對單變量估計和聯合估計方法的理論分析以及2.3中基于測點位置的機理分析結果相一致。

4 結束語

本文提出了一種基于復相關系數的輔助變量時滯聯合估計方法并將其應用于火電廠脫硝系統的NQ排放軟測量中。基于變負荷工況下的實際運行數據，結合LS-SVM算法對所提出的估計方法進行了驗證，并與不進行時滯估計、相關系數法和聯合互信息法進行了對比。結果表明，進行時滯估計后軟測量模型的準確度有了一定的提高且相比于其他時滯估計方法，所提出方法的計算速度較快、估計結果較準確，有著更好的工程應用價值。

參考文獻

[1]XIONG W，LI Y，ZHAO Y，et al.Adaptive soft sensor basedon time difference Gaussian process regression with localtime-delay reconstruction[J].Chemical Engineering Research&Design，2017，117：670-680.

[2]申貴成，管水城，孫方宇.考慮最優時滯因子時空模型的高速公路短時交通流預測[J].科學技術與工程，2018，18（24）：149-156.

[3]LOU H，SU H，XIE L，et al.Inferential model for industrialpolypropylene melt index prediction with embedded prioriknowledge and delay estimation[J].Industrial&EngineeringChemistry Research，2012，51（25）：8510-8525.

[4]李妍君，熊偉麗，徐保國一種帶過程變量時滯估計的在線軟測量建模方法[J].信息與控制，2016，45（6）：641-646.

[5]熊偉麗，李妍君.選擇性集成LTDGPR模型的自適應軟測量建模方法[J].化工學報，2017，68（3）：984-991.

[6]阮宏鎂，田學民，王平.基于聯合互信息的動態軟測量方法[J].化工學報，2014，65（11）：4497-4502.

[7]王鈞炎，黃德先.基于混合差分進化算法的軟測量時延參數估計[J].化工學報，2008，59（8）：2058-2064.

[8]阮宏鎂，田學民，王平.帶時延估計的時間差分PLS軟測量建模方法[J].石油化工自動化2013，49（6）：35-39.

[9]MONDINI V，MANGIA A L，TALEVI L，et al.Sinc-windowing and multiple correlation coefficients improveSSVEP recognition based on canonical correlationanalysis[J].Computational Intelligence and Neuroscience，2018，2018：4278782.

[10]管燕，吳和成，黃舜.基于改進DEA的江蘇省科技資源配置效率研究[J].科研管理，2011，32（2）：145-150.

[11]范德成，李昊，劉贇.基于改進DEA——以復相關系數為基準的滯后期的我國產業結構演化效率評價[J].運籌與管理，2016，25（3）：195-203.

[12]秦天牧，呂游，楊婷婷，等.SCR煙氣脫硝系統自適應混合動態模型[J].儀器儀表學報，2016，37（12）：2844-2850.

[13]馬平，李珍，梁薇.基于互信息的輔助變量篩選及在火電廠NO_x軟測量模型中的應用[J].科學技術與工程，2017，17（22）：249-254.

[14]丁續達，劉瀟，金秀章.基于壓縮感知最小二乘支持向量機的NOx軟測量模型[J].熱力發電，2018，47（3）：76-81.

（編輯：商丹丹）