我國既有普速鐵路橋梁檢定若干問題探討

王 巍，宋國華，柯在田，齊法琳，楊宜謙，董振升，王一干

（1.中國鐵道科學研究院集團有限公司鐵道建筑研究所，北京 100081；2.中國鐵道科學研究院集團有限公司基礎設施檢測研究所，北京 100081）

橋梁結構作為鐵路的重要基礎設施，其狀態是影響鐵路運輸效率的重要因素，鐵路橋梁檢定評估工作是確定橋梁運用條件、制定橋梁大修及技術改造計劃的重要技術支撐。為保證鐵路運輸安全，《鐵路技術管理規程（普速鐵路部分）》規定：技術復雜及重要的橋梁檢定，每十年不少于一次［1］。既有普速鐵路橋梁的檢定評估主要依據是鐵運函〔2004〕120 號《鐵路橋梁檢定規范》［2］（下文簡稱《橋檢規》）。

《橋檢規》是2004 年由原鐵道部組織有關部門和單位總結完成的，由于該規范沒有條文說明，部分條款在執行過程中存在一些難點，如梁體橫向振動加速度是否要低通濾波及濾波截止頻率等。近年來，結構設計計算理論、測試技術也有了較大發展。

本文結合近年來鐵路橋梁檢定工作的相關實踐，對既有普速鐵路橋梁承載能力評定方法、鋼桁梁有限元模型、鋼桁梁桿件截面應力的測試位置等問題進行探討，供既有普速鐵路橋梁檢定參考。

1 橋梁承載能力評定方法

鐵路橋梁檢定工作一般包括橋梁現狀檢查、結構及墩臺承載能力的檢算、運營性能檢驗、橋梁現場試驗等。各鐵路局每年會安排部分特殊結構橋梁的檢定任務，委托下屬橋檢隊或者鐵路行業內有相關資質的單位開展檢定工作。此類橋梁檢定一般為橋梁現狀檢查，并以現場靜載試驗來確定橋梁的承載能力和以動載試驗確定橋梁的運營性能。

為保證橋梁靜載試驗結果的可靠性，一般橋梁靜載試驗安排在無風及溫差較小的夜間進行，且靜載試驗涉及單位較多，包括總工室、工務處、機務處、車輛處、電務處、調度所、安監室等單位［3］。對于運輸任務繁忙的既有線路開展橋梁靜載試驗較為困難，且安全壓力較大，經常會出現靜載試驗無法按計劃完成的情況。

《橋檢規》并未對橋梁靜載試驗開展的前提條件進行規定。公路行業橋梁承載能力評定主要依據JTG/T J21—2011《公路橋梁承載能力檢測評定規程》［4］，該規范對公路橋梁荷載試驗開展的前提條件進行了明確規定：當檢算的作用效應與抗力效應的比值在1.0 ～1.2 時，應通過荷載試驗評定承載能力［4］。從實踐情況看，公路橋梁通過外觀檢查和承載能力檢算，可以及時發現病害橋梁，也可以定量給出橋梁的承載能力。與靜載試驗相比，橋梁外觀檢查和承載能力檢算更為簡便、經濟，對正常的交通影響較小。

相比于公路橋梁，既有普速鐵路橋梁活載更為明確，貨車車輛超載情況極少，開展承載能力檢算更為簡便，對鐵路運輸影響更小，且更為經濟。因此，對于既有普速鐵路運營荷載沒有較大變化或未出現缺陷、損傷的橋梁，建議通過結構檢算確定橋梁承載能力；對于出現缺陷、損傷或加固改造后的橋梁，建議結合結構檢算，通過靜載試驗確定橋梁承載能力。

2 鋼桁梁有限元模型

結構的校驗系數是試驗荷載作用下測點的實測彈性變形值或應變值與相應的理論計算值的比值，反映結構實際工作狀態，結構校驗系數越小，結構的安全儲備越大。

校驗系數中的理論計算結果對校驗系數影響較大，采用有限元模型計算是得到理論計算結果的常用手段。有限元模型是靜載試驗工作的基礎，《橋檢規》給出了鋼橋按平面理論分析、橋道縱梁按簡支計算的結構校驗系數［2］。

我國鐵路鋼橋采用的桁架結構是一種空間結構，各桿件之間的連接是剛性連接，最佳的計算方法是按空間結構來分析。但是實際工作中有時仍沿用《橋檢規》簡化的計算方法，即將桁架結構分成若干個平面結構如主桁、縱梁、橫梁、平縱聯、橫向連接系、橋門架等，并假設節點為鉸接，按各自平面上的荷載來計算桿件內力。這種計算方法無法考慮節點剛性和結構空間作用的影響。

以潯江大橋為例，潯江大橋為3 孔下承式連續鋼桁梁，設計圖號為“專橋（68）0120-6”，材料為16Mn 低合金鋼，計算跨度Lp=64 m，每孔8個節間，節間長度8 m，主桁高度11 m，主桁中心距5.75 m，縱梁中心距2 m。采用MIDAS軟件分別建立平面模型（見圖1，取對稱結構的一半）和空間模型（見圖2）進行理論值計算，靜載試驗測試結果見表1。

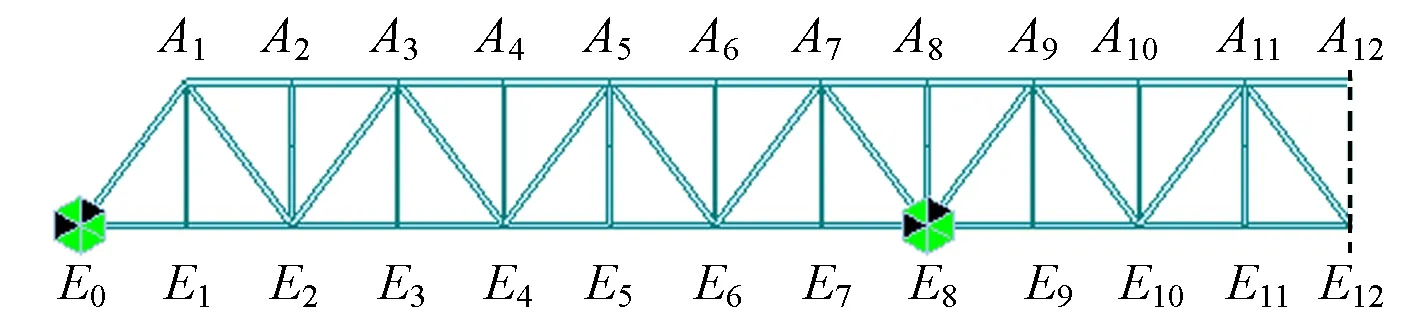
圖1 潯江大橋平面有限元模型

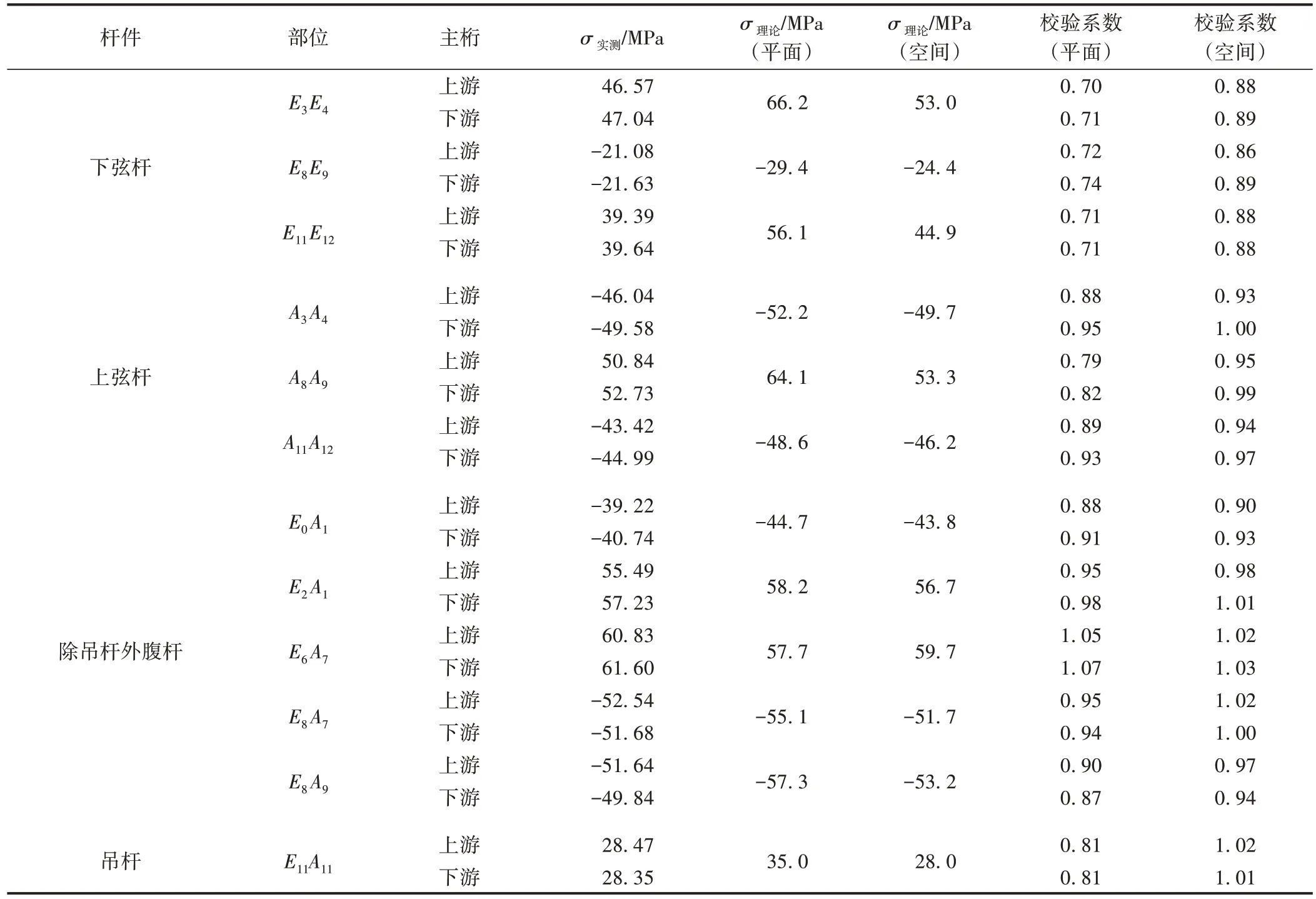
表1 潯江大橋主測桿件軸向應力測試結果

從表1中可以看出：①對于上下弦桿，以平面模型的計算結果為理論值，下弦桿的結構校驗系數在0.70～0.74，上弦桿的結構校驗系數在0.79～0.95；以空間模型的計算結果為理論值，下弦桿的結構校驗系數在0.86～0.89，上弦桿的結構校驗系數在0.93～1.00。兩者結果差距較大，空間模型更接近于實測結果。②對于吊桿和腹桿，以平面模型的計算結果為理論值，結構校驗系數在0.81～1.07，以空間模型的計算結果為理論值，結構校驗系數在0.90～1.03，兩者結果接近。

對于桁架結構的縱橫梁，縱梁的支撐狀態與支撐在橫梁上的連續梁類似，橫梁的受力狀態在一定程度上類似于彈性嵌固于主桁節點的固端梁。采用《橋檢規》簡化計算時，縱橫梁的邊界條件與其真實的邊界條件相差較大，簡化模型計算得到的理論值偏大，表2給出了潯江大橋縱橫梁結構校驗系數。可知，空間模型下的縱橫梁結構校驗系數均大于平面模型下的結構校驗系數，空間模型更接近于實測值。

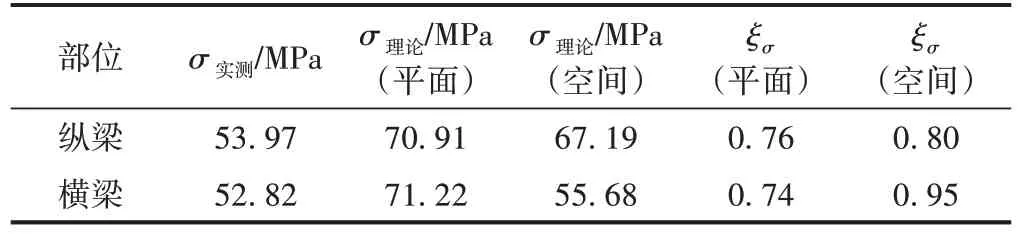
表2 潯江大橋縱、橫梁結構校驗系數ξσ

近年來，隨著有限元軟件的大規模應用，橋梁結構的計算水平已有了大幅提高，建議鐵路鋼桁梁計算模型由原來的平面模型逐漸向空間模型過渡，從而提高有限元模型計算結果的準確性。

3 鋼桁梁桿件截面應力測試位置

鋼桁梁桿件的實際受力狀態與空間梁更為接近，外荷載作用下，桿件不僅要承受軸向力作用，還要承受彎矩、剪力和扭矩的作用［5-6］。除軸向力以外的所有內力、構造及施工原因引起的桿件應力統稱為次應力。在鋼結構中，一般很難避免由于構件的偏心、節點的剛性、橋面的變形等因素引起的次應力。但我國鐵路鋼桁梁設計中大多都忽略桿件次應力的影響，按軸向受力設計桿件的截面。TB 10091—2017《鐵路橋梁鋼結構設計規范》規定：當主桁桿件截面的高度與節長之比在連續桁梁中大于1/15、簡支梁中大于1/10時應計算由節點剛性引起的次應力［7］。

如前所述，結構的校驗系數是反映結構實際工作狀態的指標，有限元模型計算中通常無法重現由于構造、施工等原因導致的桿件偏心引起的桿件次應力。現場試驗時，應變計一般沿桿件的軸向布置，測量得到的是荷載作用下桿件所受縱向正應力之和［8］。如何盡量降低桿件次應力對桿件軸向力測試結果及結構校驗系數計算結果的影響就顯得尤為重要。實踐表明，合理選擇鋼桁梁桿件應力的測試位置可以降低桿件次應力的影響［8］，但《橋檢規》并未給出鋼橋桿件截面應力的測試位置建議。

成昆線桐模甸2 號橋128 m 簡支鋼桁梁和2×64 m上承式連續鋼桁梁靜載試驗中在鋼桁梁個別桿件上布置5 個斷面的應力測點，以分析節點次應力的傳遞規律。128 m 簡支鋼桁梁選擇下游側E6E7下弦桿的E6端節點附近進行4 個斷面的次應力測試，最近的斷面距節點板為5 cm，測試斷面間距為5 cm，每個斷面布置4 個應力測點，如圖3 所示。同時，在桿件中部斷面布置4 個應力測點，端節點附近斷面與桿件中部斷面軸向應力和次應力系數對比見表3。

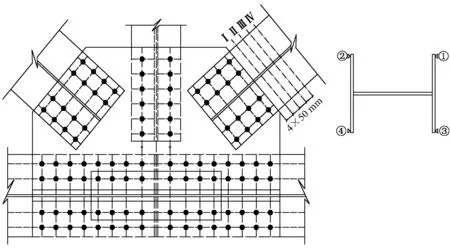
圖3 E6A7斜桿的E6端節點次應力測試斷面及測點布置

2×64 m 上承式連續鋼桁梁選擇下游側E7A8下弦桿的E8端節點附近進行4 個斷面的次應力測試，最近的斷面距節點板為5 cm，測試斷面間距為5 cm，每個斷面布置4 個測點，如圖4 所示。同時，在桿件中部斷面布置4 個應力測點，端節點附近斷面與桿件中部斷面軸向應力和次應力系數對比見表4。

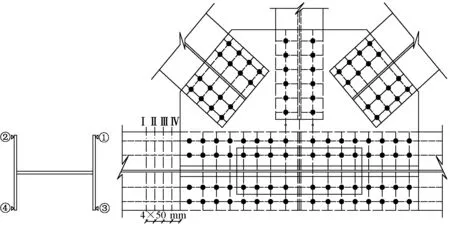
圖4 E7A8斜桿的E8端節點次應力測試斷面及測點布置

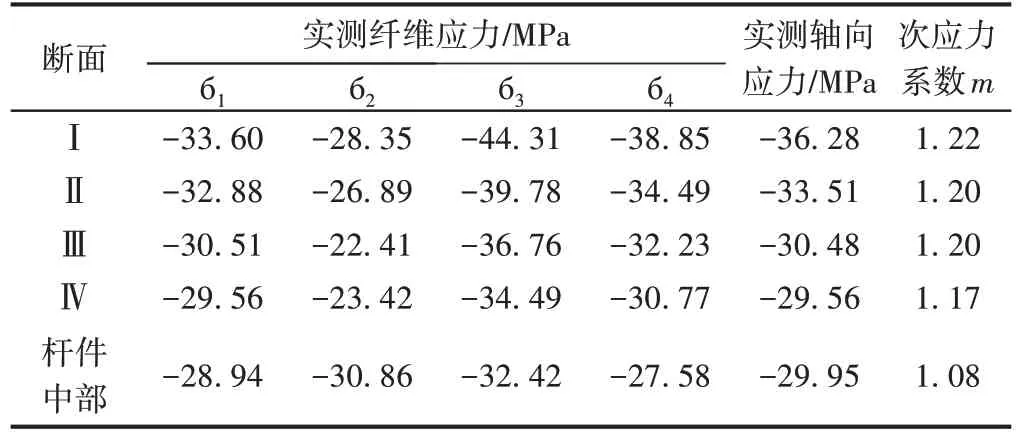
表4 E7A8斜桿E8端節點附近斷面與桿件中部斷面軸向應力和次應力系數對比

從表3 和表4 中可以看出，桿件的軸向應力由節點板邊緣向桿件中部方向呈現逐漸減小的趨勢，桿件次應力系數在桿件端部大于桿件中部。對于鋼桁梁桿件，由于節點板處受力比較復雜，桿件截面應力測試時，建議布置到靠近桿件中部的部位，以盡量降低桿件次應力的影響。

4 梁體橫向振動加速度濾波的截止頻率

日本國鐵技術研究所對跨度50 m 以下的鋼橋橫向振動加速度進行了試驗研究，結論是當橋梁的水平橫向加速度達到0.1g～ 0.2g時，車輛容易脫軌［9］。我國《橋檢規》中規定：當列車通過時，橋跨結構在荷載平面的橫向加速amax不應超過1.4 m/s2［2］。但振動加速度頻率范圍沒有明確界定。

橋梁在列車荷載作用下的橫向振動以列車加載頻率為主，引起車橋系統橫向振動的激勵源主要是車輛蛇行運動，車輛的蛇行運動頻率通常介于按自由輪對假設和按剛性定位轉向架假設計算的蛇行運動頻率之間，蛇行運動頻率要低于自由輪對的蛇行頻率，高于剛性定位轉向架假設的蛇行頻率［10］。假定車輛車輪經過磨耗后的車輪踏面等效錐度由初始狀態的0.05 變化為 0.10，C80貨車以 80 km/h 左右通過時，蛇行運動頻率介于 1.49 ～ 2.36 Hz；客車以160 km/h 左右通過時，蛇行運動頻率介于1.96 ～3.82 Hz。實測結果［11］為：C80貨車以 80 km/h 左右通過時，梁體橫向強迫振動頻率最大約為2.0 Hz；客車以160 km/h 左右通過時，梁體橫向強迫振動頻率最大約為2.2 Hz。由此可見，鐵路橋梁橫向振動以低頻為主。梁體橫向振動與運營列車車輛構架橫向加速度相關性較強，我國TB 10761—2013《高速鐵路工程動態驗收技術規范》引用歐盟規范UIC 518—2005Testing and approval of railway vehicles from the point of view of their dynamic behaviour-safety-track fatigue-ride quality的規定，車輛構架橫向加速度濾波0.5 ～10 Hz［12］。為與車體構架橫向加速度評價標準一致，梁體橫向振動加速度建議采用10 Hz低通數字濾波處理，且采用10 Hz低通濾波能夠保證梁體橫向振動頻率不高于5 Hz的振動信號不失真［13］。

5 結語

基于近年來鐵路橋梁檢定工作的相關實踐，對既有普速鐵路橋梁檢定的一些問題進行了探討，建議：

1）對于既有普速鐵路運營荷載沒有較大變化或未出現缺陷、損傷的橋梁，建議通過結構檢算確定橋梁承載能力；對于出現缺陷、損傷或加固改造后的橋梁，建議結合結構檢算，通過靜載試驗確定橋梁承載能力。

2）鐵路鋼桁梁有限元計算模型采用空間模型，以提高有限元模型計算結果的準確性。

3）由于節點板處受力復雜，鋼桁梁桿件的應力測試位置宜盡量靠近桿件中部，以降低桿件次應力的影響。

4）鐵路橋梁的橫向振動加速度建議采用10 Hz 低通數字濾波處理。

相關成果可供鐵路工作者開展既有普速鐵路橋梁檢定工作和規范修訂參考。