基于ANSYS 的錐臺形觀察窗光學性能分析

陳 薇， 張愛鋒

（中國船舶科學研究中心， 江蘇 無錫214082）

0 引 言

觀察窗是深海耐壓結構的關鍵部件，其作用包括:（1） 作為耐壓殼結構的一部分承載深海水壓；（2） 作為可視窗口使得艙內的技術人員能夠對深海環境進行直接觀察，并同步進行艙外機械手的操控作業。 可用于制造觀察窗的材料有有機玻璃、無機玻璃等，其中有機玻璃在破壞前會出現明顯的擠壓變形以提供破壞預警[1]，使艙內人員能夠及時采取措施避免進一步破壞。 因此近年來，各國載人潛水器的觀察窗材料仍以有機玻璃為主。 有機玻璃觀察窗在使用工況下可能出現結構強度降低或破壞導致的機械失效，或者結構變形導致的圖像失真，嚴重影響觀察。

Stachiw 針對有機玻璃觀察窗進行了大量短期載荷破壞試驗和長期持續加載試驗[2]，試驗得到的數據和結論是《載人壓力容器的安全標準》（ASME-PVHO）[3]的重要參考。 李向陽，崔維成[4]對深海載人潛水器的球形殼、艙口和觀察窗進行了接觸有限元分析，張端濤[5]采用接觸有限元法對觀察窗進行塑性變形分析。 廉俊盛[6]應用有限元軟件模擬觀察窗的蠕變，并與田常錄等[7]的觀察窗蠕變試驗進行對比。杜娟[5]基于有限元分析將變形后的球扇形觀察窗簡化為“彎月形透鏡”，并對其光學性能進行討論。眾多試驗研究及有限元分析顯示， 有機玻璃觀察窗在深海水壓直接加載時會產生觀察窗與窗座的相對位移和觀察窗上下表面的凹凸變形，其變形在保壓狀態下會因為蠕變進一步發展。 歐迎春[9]等提出透明材上下表面之間的厚度變化將導致透明件的局部光畸變， 并對航空透明件厚度變化引起的光學角偏差和光畸變進行了理論分析。 透明件光學畸變的試驗測量方法包括投影法[10]、網格照相法[11]等。

本文以錐臺形有機玻璃觀察窗為研究對象，在ANSYS 有限元模擬的基礎上，采用Matlab GUI 界面進行觀察窗光學角偏差和光畸變的計算，建立了評價觀察窗光學性能的理論方法，可用于觀察窗光學性能的預測與評價。

1 錐臺形觀察窗結構特點

1.1 錐臺形觀察窗的設計參數

錐臺形觀察窗及窗座的基本結構如圖1 所示，主要設計參數包括:厚度與低壓面直徑比t/D1，低壓面直徑與透光直徑比D1/Df，觀察窗錐形夾角α，觀察窗低壓面（小端）直徑D1，觀察窗與窗座接觸面摩擦系數μ 等。

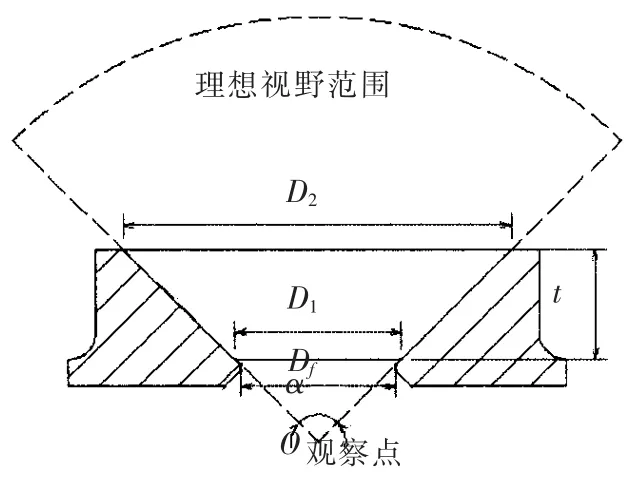
圖1 錐臺形觀察窗基本結構Fig.1 The structure of conical viewport

1.2 錐臺形觀察窗變形的有限元模擬

按規范設計α=90°，t/D1=0.4，D1=100mm，上表面邊緣45°倒角的觀察窗模型作為算例， 在ANSYS 內建立1/2 二維軸對稱模型（圖2（a））。 裝配觀察窗時通常會在錐面涂抹潤滑脂以減少摩擦力，因此可以認為接觸面摩擦系數足夠小，取μ=0.1。 有機玻璃楊氏模量為3 102 MPa，泊松比為0.35，拉伸強度為72.4 MPa，壓縮屈服應力為124.1 MPa[12]。 窗座為鈦合金結構，其楊氏模量遠大于觀察窗，因此將窗座設為目標面，將觀察窗設為接觸面，分別使用TARGE169 和CONTA172 單元建立接觸對，采用ANSYS 的面-面接觸分析，接觸容差設置為0.01，其余參數默認。 在模型對稱軸處施加對稱位移約束，對窗座施加固定位移約束。 分別在觀察窗上表面（即高壓面）處施加0～70MPa 共8 組壓力載荷。

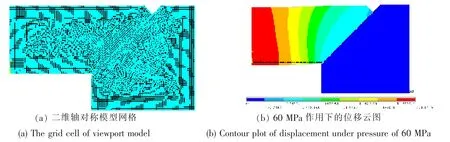
圖2 觀察窗的二維軸對稱模型網格和位移云圖Fig.2 The grid cell and contour of displacement of the viewport under pressure of 60 MPa

載荷作用下，觀察窗上下表面各節點會出現不同程度的位移（圖2（b）），可用各節點的位移來描述觀察窗的結構變形。 建立以觀察窗錐形頂點O 為原點的柱坐標系，根據每個節點的軸向與徑向位移值，可將載荷作用下觀察窗高壓面和低壓面上各節點變形后的坐標表示如圖3。

從觀察窗上下表面的曲線圖可以看出，觀察窗的變形程度與載荷有關。 加載狀態下觀察窗呈現高壓面中部坑狀凹陷，低壓面整體凸出的變形特征，與文獻[2]的試驗結果基本一致；觀察窗上下表面各點同時產生軸向和徑向位移，表面之間的厚度發生改變，變形后的整體結構可視為非球面凹凸透鏡。

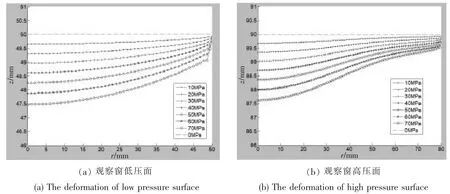
圖3 不同載荷作用下觀察窗上下表面的變形曲線Fig.3 The deformation of low pressure surface and high pressure surface of viewport under different pressure levels

1.3 曲面的偶次非球面擬合

采用最小二乘法對有限元分析得到的錐臺形觀察窗高壓面和低壓面曲線進行多項式擬合， 由于結構和載荷均具有軸對稱性，曲線擬合函數可選擇偶次多項式，形式如下:

在本文算例中，考慮擬合度和函數復雜程度，選擇6 次多項式進行擬合

應用Matlab 軟件擬合計算可得到不同載荷作用下的觀察窗表面曲線擬合函數（表1）。

表1 錐臺形有機玻璃觀察窗低/高壓面曲線擬合系數表Tab.1 The fitting coefficients of low/high pressure surface curve of conical acrylic viewport

2 錐臺形觀察窗光學性能

錐臺形觀察窗在耐壓殼上的開口較小且耐壓艙內空間有限， 人眼需靠近窗面以獲取足夠的視野范圍，因此會造成圖像失真[1]。 失真的原因之一是由光線在空氣、有機玻璃和海水之間的折射導致的光學畸變。 在觀察窗設計階段，并無實物產品進行光畸變測量試驗，可基于有限元模擬結果進行光學性能預測分析。

當人眼位于錐臺形觀察窗的錐形頂點處時， 任何一束透過觀察窗進入人眼的光線均能找到與之對應的觀察窗截平面使得入射光與出射光均在該平面上。 因此可將研究對象簡化為平面光線折射模型。 由于光線可逆，現假設人眼處為光線發射點，光線與觀察窗光軸的夾角記作視角β。

2.1 觀察窗光學角偏差的理論計算

光學角偏差是由透明體幾何尺寸和內部材料折射系數的非線性引起的光線傳播方向的改變[9]，若光線經過多次折射，則最后一次折射光線與第一次入射光線的夾角記作光學角偏差θ（圖4）。

圖4 錐臺形觀察窗的光學角偏差Fig.4 The optical angular deviation of conical viewport

圖5 觀察窗光學畸變定義Fig.5 The definition of optical distortion

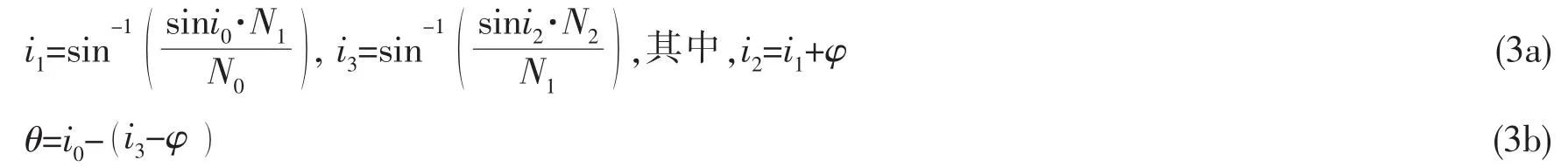
由幾何光學原理可得光在透過曲面透明體時的光線方程:式中:i0為第一次折射的入射角；i1為第一次折射的出射角；i2為第二次折射的入射角；i3為第二次折射的出射角；φ 為第一次折射點的切線和第二次折射點的切線的夾角（逆時針變化為正）；N0為空氣的折射率；N1為有機玻璃的折射率；N2為海水的折射率；θ 為光學角偏差。

視野范圍為在觀察點可觀察到距離為l 的目標面的最大面積，其半徑記作視野半徑R，有

式中:βm為最大視角；l1為第一次折射點到觀察點平面的垂直距離；l2為第一次折射點到第二次折射點的垂直距離；l3為第二次折射點到目標面的垂直距離。

2.2 觀察窗的光學畸變

光學畸變是由透明件區域光學角偏差的變化產生[9]，可用間距為Δh 的平行光透過透明件時的光學角偏差的差值進行表征（圖5），記作透明件的光畸變D[10]

式中:θ1為第一束平行光產生的光學角偏差；θ2為第二束平行光產生的光學角偏差；Δh 為兩束平行光的間距。

2.3 Matlab 計算

2.3.1 光學角偏差與視野半徑

以觀察點O 為原點建立直角坐標系（圖4），則光學角偏差可由公式（3）進行推導。 記低壓面曲線函數y= f1（x ），高壓面曲線函數y= f2（x ），已知透過觀察窗進入眼睛的某一束細光線記作直線l0。

由于光線可逆，現假設從原點O 發射光線l0:y=k0x，其中k0為光線l0的斜率；聯立低壓面曲線函數y= f1（x ）可得交點M （xm, ym）。

第一次折射過程中入射角為

出射光的斜率k2有

第一次折射的出射光直線l2表示為

聯立高壓面曲線函數y= f2（x ）求得交點N （xn, yn）。

重復公式（6），同理可推導出第二次折射過程中的入射角i2，高壓面曲線在N 點的切線斜率k3，出射角i3和出射光斜率k4。

光學角偏差為

第二次折射的出射光直線l4表示為

與直線y=l 聯立求得第二次折射的出射光與距離原點l 的目標面交于點P （xp, yp）。

在目標面的視野半徑R:

2.3.2 光學畸變

當平行光與光軸夾角為β 時，

Δh→0 時，光畸變為

式中:θ1為第一束平行光產生的光學角偏差；θ2為第二束平行光產生的光學角偏差；Δh 為兩束平行光的間距；β 為平行光與光軸的夾角；x 為入射光直線與變形前的觀察窗低壓面直線的交點的橫坐標。

3 結構變形對光學性能的影響

3.1 結構變形對光學角偏差的影響

圖6 計算觀察窗光學角偏差的Matlab GUI 界面Fig.6 The GUI interface to calculate optical angular deviation of viewport

加載后觀察窗產生變形，其變形程度與載荷有關，根據公式（6）～（9）編寫Matlab GUI 程序，建立Matlab 圖形用戶界面， 基于ANSYS 模擬結果設置觀察窗高壓面和低壓面表面曲線函數的參數，輸入項為以指定視角進入人眼的光線，由光線的可逆性即可計算出該視角的光學角偏差，并作出光線折射圖像（圖6）。 整理數據即可繪制不同載荷作用下的光學角偏差-視角曲線圖（圖7）。

可以看出，觀察窗變形程度一定時，光學角偏差隨著視角的增大而增加；視角一定時，光學角偏差隨著觀察窗變形的增大而增加；視角越大的區域的光學角偏差值對觀察窗結構的變形越敏感。

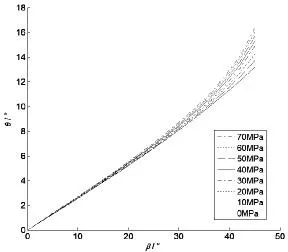
圖7 光學角偏差與視角關系曲線Fig.7 Optical angular deviation versus visual angle

3.2 結構變形對視野半徑的影響

觀察窗最大視角βm取45°，目標面與觀察點的距離l 取1 000 mm，輸入Matlab GUI 界面計算xp，輸出結果整理如表2。可以看出，隨著載荷的增加，觀察窗變形增大，透過觀察窗能看到的視野范圍隨之縮小。 載荷為70 MPa 時，視野面積較加載前縮小約20%。

表2 錐臺形有機玻璃觀察窗視野半徑表（l=1 000 mm）Tab.2 Radius of vision field of conical acrylic viewport

3.3 結構變形對光學畸變的影響

加載前觀察窗的高壓面與低壓面平行，即φ=0，i1=i2，i0=β，圖5 所示的平行光射入觀察窗時，每一束光線的入射角相等且與x 無關，代入（13）式和（12）式得此時的光學畸變D=0。

加載后觀察窗產生變形，其變形程度與載荷有關，根據Matlab 的計算結果繪制光學角偏差曲線后對其進行擬合計算并求導，得到不同角度的平行光透過觀察窗各部位的光畸變值（圖8～9）。

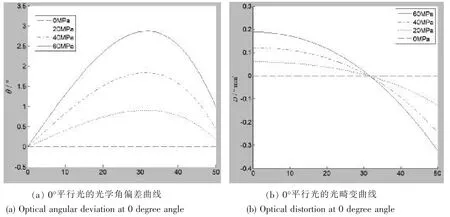
圖8 0°平行光入射時的觀察窗光學角偏差和光畸變Fig.8 Optical angular deviation and optical distortion of viewport at 0 degree angle

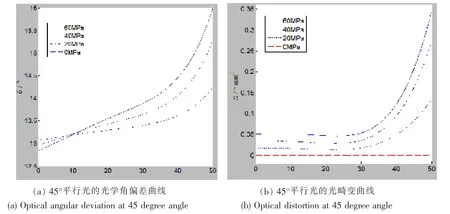
圖9 45°平行光入射時的觀察窗光學角偏差和光畸變Fig.9 Optical angular deviation and optical distortion of viewport at 45 degree angle

從曲線圖可以看出， 當觀察窗設計參數一定時， 加載前該觀察窗的光學角偏差θ 僅與視角β 有關，因此對于任意視角β，觀察窗無光學畸變；加載后，觀察窗各部位的光學畸變值與變形程度及光線角度相關；光線角度一定時，光畸變值隨著觀察窗變形的增大而增加。

4 結 語

本文采用ANSYS 接觸非線性分析方法計算了觀察窗的受壓變形狀態，同時推導了觀察窗光學角偏差和光學畸變的理論計算方法， 最后基于有限元模擬結果和理論方法建立了Matlab GUI 交互式光學角偏差計算界面。 結果表明，觀察窗的變形程度以及觀察視角均會影響觀察窗的光學角偏差和光畸變，且觀察窗的變形會導致其光學性能的下降。利用本文的理論計算方法和Matlab GUI 界面可以直觀地對觀察窗的光學性能參數進行計算與分析， 在觀察窗設計階段的光學性能預測環節有一定的應用價值。