周期為素數(shù)平方的二元序列的k-錯線性復(fù)雜度*

陳智雄, 牛志華, 吳晨煌,3

1.莆田學(xué)院應(yīng)用數(shù)學(xué)福建省高校重點實驗室, 莆田351100

2.上海大學(xué)計算機工程與科學(xué)學(xué)院, 上海200444

3.電子科技大學(xué)計算機科學(xué)與工程學(xué)院, 成都611731

1 引言

偽隨機序列在通信、密碼學(xué)等領(lǐng)域具有廣泛的應(yīng)用, 如在序列密碼中, 密文序列是由明文序列與密鑰序列異或得到, 其安全性完全依賴于密鑰序列的隨機性.因此密鑰序列的設(shè)計及其密碼學(xué)指標(biāo)是關(guān)鍵的研究方向, 序列的密碼學(xué)指標(biāo)主要包括: 平衡性、相關(guān)性、線性復(fù)雜度及其穩(wěn)定性, 等等[1–3].首先介紹序列的線性復(fù)雜度、k-錯線性復(fù)雜度的概念.

設(shè)F2= {0,1} 為二元有限域, 對于F2上周期為T的二元序列其線性復(fù)雜度(記為定義為滿足F2上的如下線性遞歸關(guān)系的最小階L

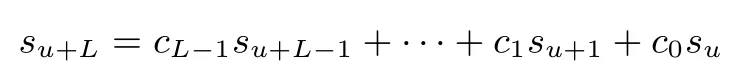
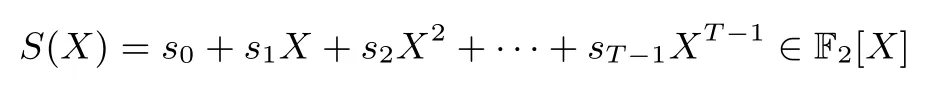
S(X)被稱為的生成多項式.那么,在F2上的線性復(fù)雜度可通過下式計算

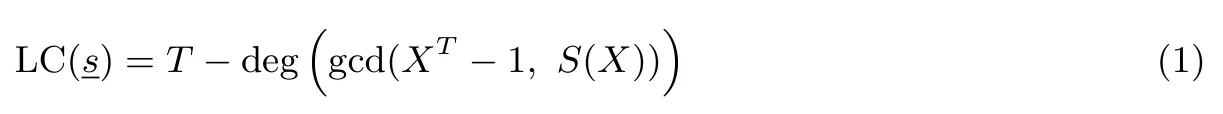
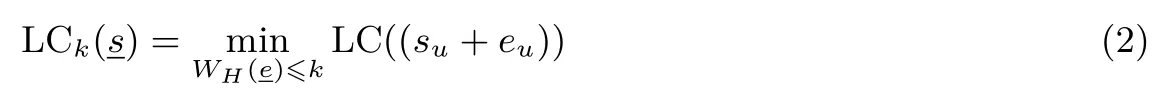
線性復(fù)雜度和k-錯線性復(fù)雜度是序列的重要密碼學(xué)性質(zhì), 它們刻畫的是序列的可預(yù)測性從而衡量該序列是否適用于密碼學(xué)領(lǐng)域.從密碼學(xué)應(yīng)用角度來說, 一個序列的線性復(fù)雜度應(yīng)盡可能的大, 并且序列在改變?nèi)舾身椇笃渚€性復(fù)雜度不應(yīng)明顯降低[1,2].

早在 1969 年, Massey 設(shè)計了一個算法用于計算序列的線性復(fù)雜度[5], 往后的文獻中稱之為 BM 算法.1983 年, Games 和Chan[6]給出了周期為2n的二元序列的線性復(fù)雜度的快速算法, 算法的時間復(fù)雜度遠低于通用的 BM 算法.1993 年, Stamp 和 Martin[4]對 Games-Chan 算法進行了擴展, 引入一維代價數(shù)組, 提出了周期為2n的二元序列的k-錯線性復(fù)雜度的快速算法.

本文我們主要討論周……