受迫振動中作用力做功的特征分析

王睿博

(電子科技大學信通學院 四川 成都 611731)

王啟州

(電子科技大學英才學院 四川 成都 611731)

吳彥旭

(電子科技大學信通學院 四川 成都 611731)

鄔劭軼 吳明和 滕保華

(電子科技大學物理學院 四川 成都 611731)

1 引言

受迫振動是物理學中一個重要的內容，在各個大學物理教科書和眾多學術文獻中均有介紹和討論[1～5].但是在教科書和相關論文中多是討論位移共振和速度共振，即討論通過改變策動力的頻率而導致振子系統的振幅、速度等極大的情形，同時對速度共振時系統中各個力的功與共振時速度極大值的相互關系也鮮見討論.

本文將策動力頻率和阻尼系數選作自變量，分別計算在兩個不同參數坐標下阻尼力以及策動力和回復力3個力所做的功，并通過分析阻尼力的功與速度共振的相互關系，更深入了解受迫振動中的共振現象.

2 受迫振動中功的表達式

設質量為m，勁度系數為κ，阻尼系數為γ的振子系統，在回復力-κx，阻尼力-γv和策動力F0cos(ωt)3個力作用下做受迫運動，其動力學方程為

(1)

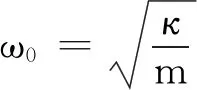
系統達到穩態后，其運動學方程可表示為

x=Acos(ωt+φ0)

(2)

其中A為振幅，φ0為位移的初相，它們分別為[1,2]

(3)

(4)

(5)

(6)

(7)

3 受迫振動中作用力做功的特點分析

3.1 速度共振頻率下作用力做功的特點

當一個振子系統做受迫振動時，可以通過改變策動力頻率來分析系統的共振現象，從而看到人們常說的位移共振、速度共振等物理現象.求解A(ω)和ωA(ω)的極值，可以得到位移共振和速度共振時所對應的兩個共振圓頻率分別為

(8)

為了深入理解速度共振時系統中的能量轉換情況，我們以策動力頻率為自變量分別來分析阻尼力以及策動力和回復力等3個力所做的功.

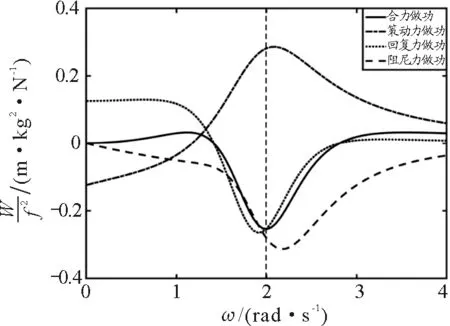
圖1 阻尼力、策動力、回復力及合力的做功曲線

圖1中的參數分別設定為：阻尼β=0.7 N/(kg·m/s)，固有圓頻率ω0=2 rad/s，策動力幅值f=1 N/kg.圖中線虛線、點劃線和點虛線3條虛線分別代表阻尼力以及策動力和回復力所做的功，而實線代表合力所做的功，平行于縱軸的虛線標記的頻率為速度共振圓頻率ω0.

可以看出，阻尼力、策動力、回復力等3個分力所做的功都是關于策動力頻率的單峰形態，但是做功峰值對應的頻率不同，分別位于系統速度共振頻率的左右.阻尼力和策動力做功的極值對應的頻率大于系統速度共振頻率，而回復力做功的極值對應的頻率則小于速度共振頻率.也就是說，系統處在速度共振頻率下，3個分力做的功都不是其極值.

但是在速度共振頻率下，策動力和阻尼力在整個過程中始終相互抵消，即

Fdriving=fcos(ω0t)

(9)

fdamping=-2βv=

(10)

這就意味著，在速度共振時，策動力做的正功始終彌補阻尼力的負功，于是此時系統的功完全由回復力決定，即在速度共振時系統相當于處于沒有外力的簡諧運動狀態，使得合力做功為極大值，從而使振子的速度為極大值.從圖1可以明顯看出，在速度共振時，3個分力做的功在ω0處都不是其極值，但是合力的功在ω0處卻是其極值.

3.2 小于或大于速度共振頻率時阻尼做功的特點

下面分析策動力頻率不等于速度共振頻率時，阻尼系數對阻尼力做功的影響.我們以系統阻尼系數作為自變量，可以得到在策動力頻率和固有頻率保持固定的條件下，阻尼力做功對阻尼系數的依賴關系圖.圖2為阻尼系數坐標下阻尼力做功的圖像，其中參數設置為固有圓頻率ω0=2 rad/s、策動力幅值f=1 N/kg.

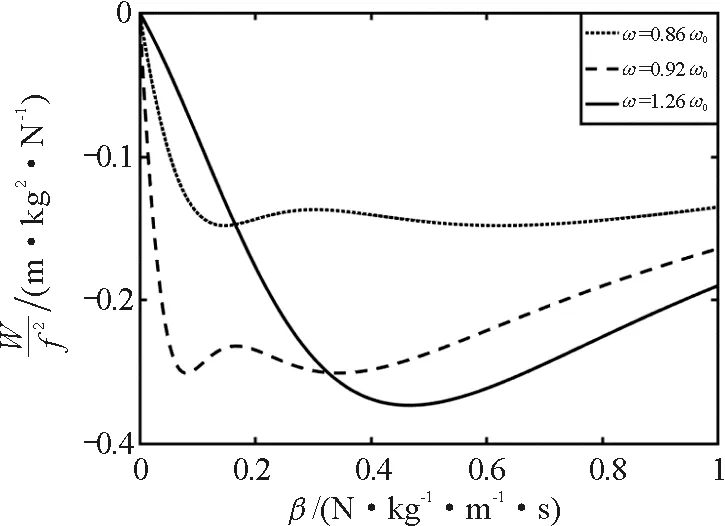
圖2 阻尼系數坐標下阻尼力的功

可以發現，在阻尼系數坐標下阻尼力做功的特點比較特殊，其做功曲線呈現出多峰形態，并且峰值對應的阻尼系數各不相同.從圖2中點虛線和線虛線可以看出，當策動力頻率小于固有頻率時，阻尼力做的功是關于阻尼系數的雙峰結構，即阻尼力功的極值對應兩個不同的阻尼系數，根據阻尼力功的表達式Wf，可以得到雙峰的位置和功的極值分別為

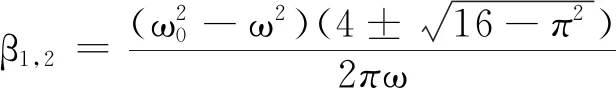
(11)

這表明，阻尼力在兩個不同阻尼系數下都會達到其功的極值狀態，且極值相等.

當策動力頻率大于固有頻率時，阻尼力的功呈現單峰形態，如圖2中實線所示.

4 結論

本文分別從策動力頻率和阻尼系數兩個不同角度，分析了阻尼力以及策動力和回復力3個力所做的功，以及阻尼力的功與速度共振的一些細節關系，發現了在速度共振頻率下，3個分力的功都不是其極值，但是其合力的功卻是極值；而當策動力頻率小于固有頻率時，存在兩個阻尼系數使阻尼力的功都會達到極值狀態，從而對共振現象有了更加深入的認識.