一種基于松弛算法改進(jìn)的最小組播樹生成方法
向雄,李羨童
(廣州大學(xué)華軟軟件學(xué)院網(wǎng)絡(luò)技術(shù)系,廣州510990)
0 引言
構(gòu)建代價(jià)最小的組播樹是計(jì)算機(jī)網(wǎng)絡(luò)領(lǐng)域一個(gè)經(jīng)典的問題,組播樹問題一般化就成了斯坦納樹(Steiner Tree,ST)問題[1]。假設(shè)R 是圖G 的頂點(diǎn)子集,則ST 就是一個(gè)連通R 中所有頂點(diǎn)且代價(jià)最小的子圖。這類問題應(yīng)用價(jià)值非常廣泛,例如網(wǎng)絡(luò)層RP 組播和單源組播、應(yīng)用層的P2P 組播等。組播技術(shù)常見于流媒體、文件傳輸以及訂閱/發(fā)布的消息模型等各種網(wǎng)絡(luò)應(yīng)用,如視音頻會(huì)議、網(wǎng)絡(luò)直播、點(diǎn)播、多人游戲程序等。近年來隨著VLSI 的發(fā)展,ST 算法被用來優(yōu)化集成電路設(shè)計(jì),應(yīng)用范圍延伸到了芯片設(shè)計(jì)領(lǐng)域。
研究表明,ST 是一個(gè)NP 難問題[2],其確定性算法都具有指數(shù)級(jí)的時(shí)間復(fù)雜度。因此在應(yīng)用性研究方面重點(diǎn)聚焦在尋找多項(xiàng)式時(shí)間內(nèi)近似算法或者解決某些特殊情形,文獻(xiàn)[3]對(duì)各類確定性算法和啟發(fā)式算法進(jìn)行了全面的分析和比較。
隨著NFV 及5G 等技術(shù)的發(fā)展,近年來網(wǎng)絡(luò)有向SDN 新型網(wǎng)絡(luò)演進(jìn)的趨勢[4]。相比傳統(tǒng)路由器中的嵌入式控制系統(tǒng),SDN 中執(zhí)行算法的控制器部署在高性能的服務(wù)器集群上,并且可以利用全局信息對(duì)網(wǎng)絡(luò)進(jìn)行精確地編排,高性能的傳輸算法對(duì)充分利用網(wǎng)絡(luò)基礎(chǔ)設(shè)施的作用非常巨大。
為此,本文對(duì)組播傳輸算法展開了研究,提出了一種在松弛算法基礎(chǔ)上進(jìn)行環(huán)破除的組播樹生成方式,后面簡稱RR(Relax based Ring)算法。該方法在利用松弛算法生成傳播樹的同時(shí)發(fā)現(xiàn)可優(yōu)化環(huán),然后破除這些可優(yōu)化環(huán)即可得到代價(jià)更小的傳播樹。本文用到的符號(hào)及定義如下,參見圖1,其中加粗的線條表示傳播路徑。
G:無向帶權(quán)連通圖。G=(V,E)是一個(gè)包含n 個(gè)頂點(diǎn)的圖,V 是G 中的頂點(diǎn)集,E 是G 中的邊集,E={(u,v)|u,v∈V}。
s:組播源,s∈V。
F(u,v):表示兩節(jié)點(diǎn)之間的傳輸代價(jià),當(dāng)u,v 相鄰時(shí)它就邊(u,v)上的權(quán)值,當(dāng)u,v 不相鄰時(shí)表示從u 沿著組播樹到達(dá)v 時(shí)所經(jīng)過的邊的代價(jià)和,
R:組播的接收者集合,R?V。R 中的節(jié)點(diǎn)稱為R節(jié)點(diǎn)
P(u,v):表示樹中兩頂點(diǎn)u,v 之間路徑,是從u 沿樹到達(dá)v 所經(jīng)過的邊集。
W(u):表示以u(píng) 為樹根的子樹上所有邊的代價(jià)和。
T:G 中的子樹,T=(VT,ET),T?G,VT?V,ET?E。
RR 問題與ST 問題目標(biāo)一致,可描述為:構(gòu)造以s為根的樹,使得R ?VT且W(s)最小。
本文結(jié)構(gòu):先介紹相關(guān)研究,然后介紹松弛算法及其過程,隨后對(duì)可優(yōu)化環(huán)進(jìn)行定義并論證其存在性和優(yōu)化性,分析可優(yōu)化環(huán)之間的關(guān)系及破除順序,最后給出算法的運(yùn)行效果,得出結(jié)論。

圖1 RR樹示例
1 相關(guān)研究
目前與此相關(guān)的研究成果主要有KMB、SPH、ADH及LMC 等算法。KMB[5]是一種經(jīng)典的組播樹生成算法,它首先使用Prim 或Kruskal 算法從圖G 中找出由組播節(jié)點(diǎn)所形成的子圖的最小生成樹(MST),然后將此MST 代回到圖G 中,剪除掉無關(guān)路徑就得到了一棵組播樹,時(shí)間復(fù)雜度為O(mn2)。SPH(Shortest Path Heuristic)[6]算法也稱作MPH(Minimum Path Heuristic),它首先將源點(diǎn)添加到組播樹,然后依次將與樹最近的節(jié)點(diǎn)添加到樹中,直到所有組播節(jié)點(diǎn)均已加入,復(fù)雜度同KMB。ADH(Average Distance Heuristic)[7]算法則選擇一個(gè)節(jié)點(diǎn)作為中心節(jié)點(diǎn),然后以它為中心生成|S|+|R|棵子樹,再用最短路徑依次將這些子樹連接起來得到最終的組播樹,時(shí)間復(fù)雜度為O(n3)。SPH 和ADH 都宣稱在性能上略優(yōu)于KMB。還有一種樸素組播路由算法[8]宣稱其性能超越了KMB,這是一種基于權(quán)重的貪婪算法。當(dāng)一個(gè)新節(jié)點(diǎn)加入到組播樹時(shí),它會(huì)選擇一條到樹中最短的鏈路進(jìn)行連接。LMC[9]算法采用類似于Dijkstra 算法來尋找源到其他節(jié)點(diǎn)的最短路徑,當(dāng)遍歷到一個(gè)R 節(jié)點(diǎn)時(shí),LMC 會(huì)將它的dist 值置0。當(dāng)所有R 節(jié)點(diǎn)都被包含進(jìn)組播樹時(shí)算法結(jié)束。其他的與最小代價(jià)樹有關(guān)的算法還有擴(kuò)展的Dijkstra 算法[10]、Bellman-Ford 算法及SPFA 算法[11]等。SPFA 算法并沒有給出正確的嚴(yán)格證明,它在Bellman-Ford 算法基礎(chǔ)上添加了隊(duì)列功能,各節(jié)點(diǎn)可以循環(huán)入隊(duì),隊(duì)列為空時(shí)結(jié)束算法,這樣可以減少組播總代價(jià),但在極端情形下有可能陷入死循環(huán)。
近年來,有人嘗試?yán)弥悄芩惴ê蜋C(jī)器學(xué)習(xí)等技術(shù)來研究ST 問題[12-14]。文獻(xiàn)[13]利用基于蟻群的并行算法在GPU 上取得了比KMB 算法代價(jià)優(yōu)化8%運(yùn)行速度快2 倍的效果。文獻(xiàn)[14]在解決直線斯坦納最小樹問題時(shí)利用KNN 算法來縮小解空間,提升了解的質(zhì)量,主要應(yīng)用于芯片領(lǐng)域。文獻(xiàn)[15]提出一種免疫算法把每個(gè)steiner 點(diǎn)看作疫苗,然后不斷地把它“接種”到最小生成樹上,多次迭代后可以達(dá)到99.95%的最優(yōu)路徑。這類算法的共同點(diǎn)是應(yīng)用于專門的領(lǐng)域,對(duì)設(shè)備有特殊的要求。
當(dāng)前算法都是近似算法,都無法達(dá)到最優(yōu),在生成樹代價(jià)方面還存在進(jìn)一步降低的空間。數(shù)據(jù)模擬表明,在減小總代價(jià)方面,RR 算法能達(dá)到和超越之前的最優(yōu)水平。
2 松弛算法
定義一松弛算法。對(duì)于每個(gè)頂點(diǎn)v∈V,都設(shè)置一個(gè)屬性dist(v),表示從源點(diǎn)S 到v 的最短路徑上權(quán)值的上界,初值設(shè)置為無窮大。算法的執(zhí)行過程是不停地尋找dist 值最小的頂點(diǎn)u,然后訪問u,訪問時(shí)遍歷u的每一個(gè)鄰居j,如果滿足松弛條件p,則執(zhí)行松弛過程q,并將j 的父節(jié)點(diǎn)標(biāo)記為u,記作π(j)=u。。
松弛算法是基于連通圖的,所以源到所有R 節(jié)點(diǎn)都有路徑可達(dá),初始狀態(tài)下當(dāng)s 與目標(biāo)節(jié)點(diǎn)沒有直接連接就當(dāng)作是一條權(quán)值無窮大的邊,然后不斷地試圖把這條邊拆開,用通過其他節(jié)點(diǎn)中轉(zhuǎn)的代價(jià)更小的邊集來替換,這樣兩點(diǎn)之間一條邊就變成了多條邊,變得“松弛”了。
Dijkstra 及擴(kuò)展的Dijkstra、LMC 等都屬于松弛算法,其松弛條件p 均為:dist[j]>dist[u]+F(u,j),只是松弛過程q 不一樣。利用Dijkstra 松弛算法可以得到如圖1(b)中加粗線條所示的松弛樹,使用環(huán)破除方法可以進(jìn)一步降低其總代價(jià)。
3 可優(yōu)化環(huán)
定義二可優(yōu)化環(huán)路。對(duì)節(jié)點(diǎn)a 的鄰居b 進(jìn)行松弛操作時(shí),記a,b 共同的最鄰近祖先節(jié)點(diǎn)為n,如果滿足條件:①b 已經(jīng)被訪問過;②F(a,b)≥F(n,b)-F(n,a);③max{F(n,a),F(xiàn)(n,b)}>F(a,b),則邊(a,b)與路徑P(n,a)和P(n,b)所構(gòu)成的環(huán)路是一個(gè)可優(yōu)化環(huán)路,記作環(huán)(a,b)。n 是環(huán)(a,b)的分支節(jié)點(diǎn),a 是環(huán)的起點(diǎn),b 是環(huán)終點(diǎn)。

圖2 可優(yōu)化環(huán)
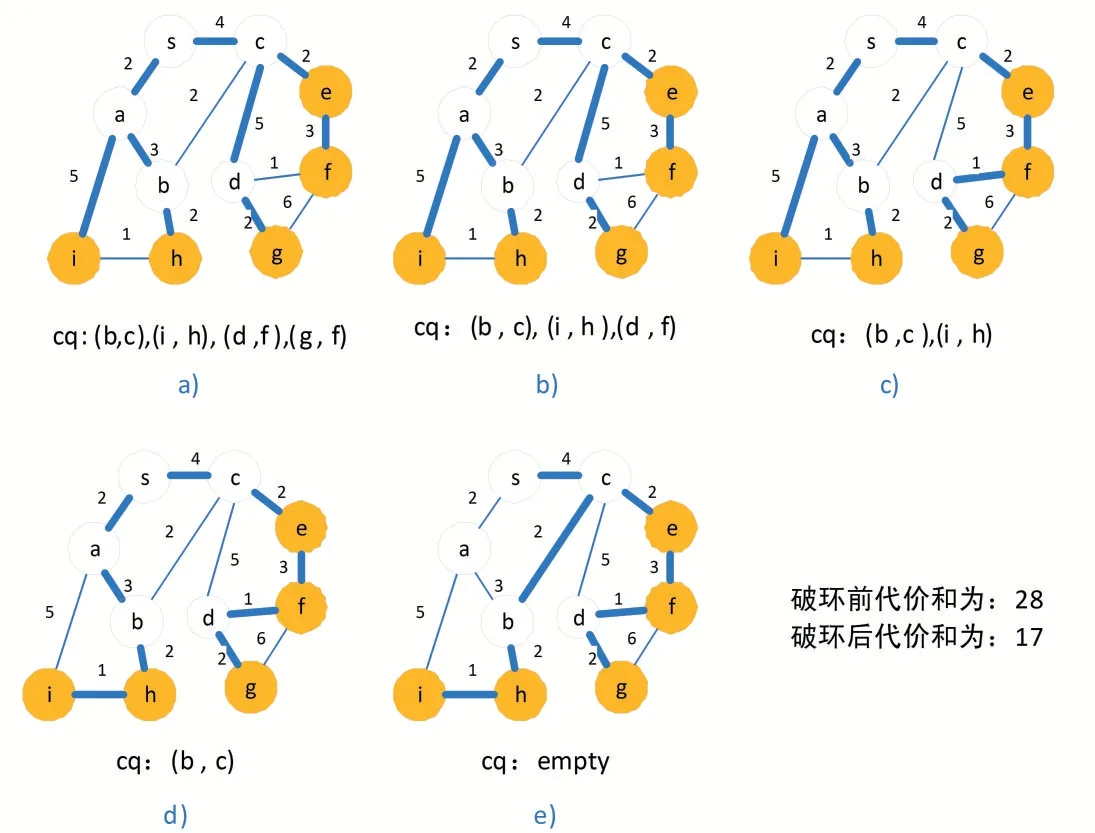
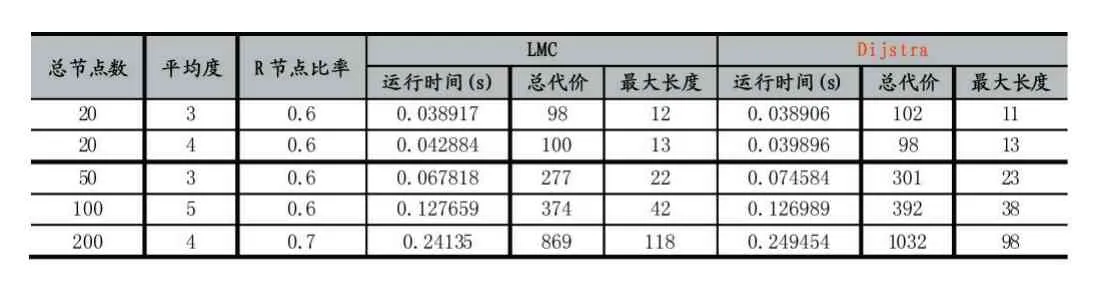
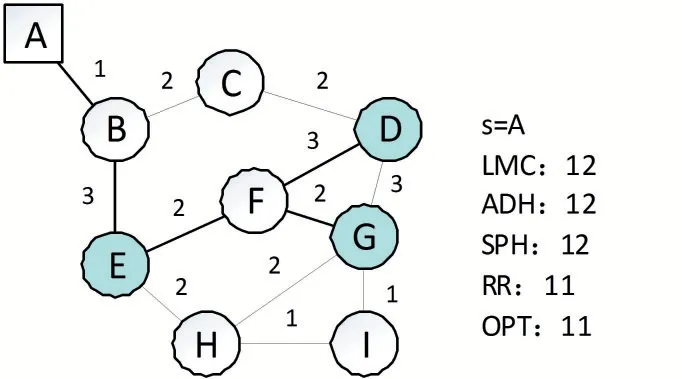
例如在圖2(a)中,dist(n)=8,dist(a)=12,dist(b)=15,則F(n,a)=dist(a)-dist(n)=4,F(xiàn)(n,b)=dist(b)-dist(n)=7,因?yàn)镕(n,b)-F(n,a)=7-4=3 定義二中的條件2 若不滿足,則根據(jù)定義一,它就滿足了松弛條件,那么a 就成為b 在組播樹上的父節(jié)點(diǎn),這種情形是不用優(yōu)化的,因?yàn)榇藭r(shí)以n 為根的子樹代價(jià)已經(jīng)是最小的了。 定義二中條件3 的作用是過濾掉一些無法優(yōu)化的環(huán)。max{F(n,a),F(xiàn)(n,b)}>F(a,b)不滿足,那就意味著F(a,b)會(huì)大于或等于P(n,a)和P(n,b)路徑上任何一條邊的權(quán)值,這樣一來不管哪條邊被邊(a,b)替換,只可能增加樹的總代價(jià),再進(jìn)行優(yōu)化是沒有意義的。 RR 算法中的核心思想就是找出松弛樹中的可優(yōu)化環(huán)進(jìn)行破除,破除時(shí)只需簡單地去掉環(huán)中的最大邊。我們知道,去掉環(huán)路中的一條邊并不會(huì)影響圖的連通性,這樣就可達(dá)到降低組播樹總代價(jià)的目標(biāo)。 定理一去掉可優(yōu)化環(huán)中的最大邊可以降低樹的代價(jià)。 定義三中轉(zhuǎn)節(jié)點(diǎn):如果一個(gè)可優(yōu)化環(huán)上某節(jié)點(diǎn)不是R 節(jié)點(diǎn),并且它除了環(huán)中的兩條邊之外其余的邊都不在任何樹中,也不在其他可優(yōu)化環(huán)上,則應(yīng)把這兩條邊合并為一條邊,這個(gè)節(jié)點(diǎn)叫中轉(zhuǎn)節(jié)點(diǎn)。如圖2(b)中的節(jié)點(diǎn)a。 定理二環(huán)破除之前先聚合中轉(zhuǎn)節(jié)點(diǎn)更能降低代價(jià)。 證明:中轉(zhuǎn)節(jié)點(diǎn)只是一種中間轉(zhuǎn)發(fā)節(jié)點(diǎn),既不是分叉點(diǎn),也不是目標(biāo)節(jié)點(diǎn),聚合它之后可以得到代價(jià)值更大的邊,從而增加在進(jìn)行環(huán)優(yōu)化時(shí)被去掉的可能性,如果被去掉了,則降低的代價(jià)值更大,從而得到的組播樹總代價(jià)更小。 例如在圖2(b)所示的以s 為分支節(jié)點(diǎn)的環(huán)(b,c)中,a 是一個(gè)中轉(zhuǎn)節(jié)點(diǎn),聚合之前環(huán)路中最大邊為F(s,c)=4,環(huán)優(yōu)化結(jié)果為W(s)=7。聚合中轉(zhuǎn)節(jié)點(diǎn)a 后,sab被看作是一條邊,那么最大邊為F(s,b)=5,聚合中轉(zhuǎn)節(jié)點(diǎn)后的再進(jìn)行環(huán)優(yōu)化結(jié)果為W(s)=6。破環(huán)前的父子關(guān)系為{π(b)=a,π(a)=s,π(c)=s},破環(huán)后節(jié)點(diǎn)a 被合并路徑P(s,b)被視作一條權(quán)重為5 的邊去掉了,增加了(b,c)邊,則節(jié)點(diǎn)間父子關(guān)系修改為{π(b)=c,π(c)=s}。 RR 算法主要過程是生成松弛樹的同時(shí)生成可優(yōu)化環(huán),然后按序逐個(gè)破除可優(yōu)化環(huán)。具體算法如下: 輸入:圖G,起點(diǎn)s Case1.G=,此時(shí)G內(nèi)冪零,由定理5可知若m≥2,P?(G)連通且diam(P?(G))≤4;若m=1,由定理6的證明可知CP(Q)=1,再利用定理5可知真冪圖P?(G)不連通且連 輸出:多播樹T 一、初始化數(shù)組T、dist、opened;初始化棧cq;dist[s]=0;opened←{s}。 二、while opened≠Φ do: (1)i=pop(opened,0);T←{i} (2)遍歷i 的每一個(gè)鄰居節(jié)點(diǎn)j: ①若滿足松弛條件,則:dist[j]=dist[i]+F(i,j),π(j)=i;open←{j};opened 升序重排;continue; ②若j 已訪問過,則進(jìn)一步判斷環(huán)(i,j)是否滿足定義二條件,若是則cq←{(i,j)}; 三、while cq≠Φ do:(1)取出棧頂環(huán)(i,j); (2)對(duì)節(jié)點(diǎn)i,j 進(jìn)行父節(jié)點(diǎn)回溯,找到環(huán)(i,j)的分支節(jié)點(diǎn)n; (3)合并Path(i,n)和Path(j,n)上的中轉(zhuǎn)節(jié)點(diǎn)。 (4)去掉Path(i,n)∪Path(j,n)∪(i,j)中的最大邊;修改相關(guān)節(jié)點(diǎn)的父子關(guān)系; 四、for node in T:#剪除末端非R 節(jié)點(diǎn)的分支,末端節(jié)點(diǎn)度為1 1.if degree(node)=1 and node 不是R 節(jié)點(diǎn): ①從node 上溯父節(jié)點(diǎn),刪除度為2 的父節(jié)點(diǎn),直到父節(jié)點(diǎn)度大于2 算法的第二步首先驗(yàn)證松弛條件,若成立則加入松弛樹,否則驗(yàn)證可優(yōu)化環(huán)條件,如果是則將其入棧。第三步的執(zhí)行過程如圖3 所示。開始時(shí)cq 棧中有四個(gè)環(huán),在步驟a)中,從cq 棧頂取出環(huán)(g,f),破環(huán)的結(jié)果是刪除邊(g,f),無需對(duì)路徑作任何更改。在步驟b)中,從棧頂取出邊(d,f),環(huán)優(yōu)化的結(jié)果是刪除邊(c,d)。得到c)所示的圖。在步驟d)中需要破除的環(huán)(b,c),此時(shí)節(jié)點(diǎn)a 點(diǎn)為中轉(zhuǎn)節(jié)點(diǎn),于是合并sa 和ab 為一條邊,記為sab,它就成了環(huán)(b,c)上要被去掉的最大邊,這樣就得到了步驟f)所示的最終結(jié)果 圖3 Dijkstra樹的環(huán)破除過程 RR 算法第三步中的2、4 小步分別進(jìn)行父節(jié)點(diǎn)回溯和環(huán)破除過程,下面分別說明之。 (1)父節(jié)點(diǎn)回溯 父節(jié)點(diǎn)回溯的目的是為了找到環(huán)(i,j)的分支節(jié)點(diǎn),首先上溯到i,j 的共同最終祖先節(jié)點(diǎn)s,也就是組播源,分別得到各自的父節(jié)點(diǎn)列表iparents 和jparents,然后將兩個(gè)列表倒序排列,那么兩個(gè)列表中前k 個(gè)相同元素就是i 和j 節(jié)點(diǎn)所在的公共分枝,公共分枝的最后一個(gè)節(jié)點(diǎn)環(huán)(i,j)的分支節(jié)點(diǎn)。主要Python 實(shí)現(xiàn)代碼如下。 temp=i while g.node[temp]!=s: temp=g.node[temp][parent] iparents.append(temp) temp=j while g.node[temp]!=s: temp=g.node[temp][parent] iparents.append(temp) iparents.reverse();jparents.reverse() for m,n in zip(iparents,jparents): if m!=n:return iparents[iparents.index(m)-1] (2)環(huán)破除過程 環(huán)破除的主要過程是去掉環(huán)路中的最大邊,將最大邊的子節(jié)點(diǎn)及其以下的子節(jié)點(diǎn)反向連接。主要Python 實(shí)現(xiàn)代碼如下。其中Circle 函數(shù)返回環(huán)中邊集,每一條邊的表示形式為元組(u,v,w),u 是v 在樹中的父節(jié)點(diǎn),w 為權(quán)重。為避免冗長說明,本處省略了中轉(zhuǎn)節(jié)點(diǎn)合并過程。 def BreakCircle(i,j,n): edgelist=Circle(i,j) edge=max(edglist,key=lambda d:d[2])#找到權(quán)值最大邊 index=edgelist.index(edge) while True: child=edge[1] if child==j:#如果最大邊的終邊為環(huán)終點(diǎn)j,則j 父節(jié)點(diǎn)設(shè)為i g.node[j][parent]=i;break elif child==i:#如果最大邊的終邊為環(huán)起點(diǎn)i,則i 父節(jié)點(diǎn)設(shè)為j g.node[i][parent]=j;break else:#否則一直下溯,將下一條邊的起點(diǎn)變成上一條邊終點(diǎn)的父節(jié)點(diǎn) next_edge=edgelist[index+1] g.node[child][parent]=next_edge[0] index=index+1 g.edges.remove(edge) edge=next_edge 假設(shè)問題的規(guī)模(即G 中的頂點(diǎn)數(shù))為N。算法的第二步共需要循環(huán)N 次,因?yàn)槊總€(gè)節(jié)點(diǎn)都會(huì)進(jìn)入到opened 表一次。循環(huán)內(nèi)部需要將opened 重新排序。采用Python 實(shí)現(xiàn)時(shí),其列表對(duì)象的sort 方法默認(rèn)是采用Timsort[16]排序算法,它結(jié)合了合并排序和插入排序的特點(diǎn),能充分利用已經(jīng)排好序的數(shù)據(jù)特點(diǎn),是一種非常高效的算法。Timsort 算法的時(shí)間復(fù)雜度在最壞的情形下(例如隨機(jī)序列)為O(log(n!)),最好情形下不超過O(n)。opened 表中元素是依次加入的,每次排序時(shí)大部分元素都處于有序狀態(tài),正好符合Timsort 算法的最佳情形。在循環(huán)內(nèi)部遍歷節(jié)點(diǎn)的k 個(gè)鄰居,訪問每個(gè)鄰居時(shí)需要m 個(gè)操作,故其時(shí)間復(fù)雜度為N*N*k*m,由于m 和k 都是與規(guī)模無關(guān)的常數(shù)故們可以估算得出第二步的時(shí)間復(fù)雜度不超過O(N2)。 算法第三步while 循環(huán)內(nèi)部的主要工作是尋找環(huán)的分支節(jié)點(diǎn)破環(huán)。最壞的情況為分支節(jié)點(diǎn)為s,i,j 回溯時(shí)兩條路徑不相交地走完了圖中所有節(jié)點(diǎn)。假設(shè)i所在的路徑上節(jié)點(diǎn)數(shù)為k,則j 所在的路徑節(jié)點(diǎn)為Nk-3,故其尋找共同父節(jié)點(diǎn)的時(shí)間復(fù)雜度為k*(N-k-3)。破環(huán)時(shí)要比較(N-1)次邊大小,如果要進(jìn)行中轉(zhuǎn)節(jié)點(diǎn)合并,則可以減少比較操作,但增加了求和操作,所以比較或求和的總次數(shù)還是(N-1)次,可算得操作次數(shù)為k*(N-k-3)+(N-1)≈k*(N-k)+N,當(dāng)k=N/2 時(shí)值達(dá)到最大,為N2/2+N,時(shí)間復(fù)雜度量級(jí)為O(N2)。最好的情況。i、j 的共同父節(jié)點(diǎn)就是它們各自的直接上級(jí)節(jié)點(diǎn)。此時(shí)環(huán)路中只有三條邊,只需3 次比較即可完成。由此可見,即使是最壞情況,其時(shí)間復(fù)雜度量級(jí)也不會(huì)超過Ο(N2)。因此第三步時(shí)間復(fù)雜度為O(N2*M),其中M 為環(huán)的個(gè)數(shù)。下面分析M 的取值可能范圍。 假設(shè)G 是一個(gè)隨機(jī)網(wǎng)絡(luò),其中每條邊的代價(jià)值量化到1~10 十個(gè)等級(jí),則?(u,v)∈E,Cost(u,v)是一個(gè)隨機(jī)變量,記作X,其概率分布為: X 的概率母函數(shù)為: 在圖2 所示的可優(yōu)化環(huán)中,Path(n,a)和Path(n,b)中邊數(shù)分別記為Na和Nb,Na和Nb兩個(gè)獨(dú)立同分布的隨機(jī)變量,很明顯它們符合泊松分布特點(diǎn),其概率母函數(shù)G(s)為: 令Ya=Cos(tn,a),則Ya=也是隨機(jī)變量,根據(jù)(2)和(3),由數(shù)學(xué)性質(zhì)可得Ya的概率母函數(shù)H(s)為: 由式(4)即可計(jì)算出Ya和Yb的概率分布。 由定義二可知,在分支節(jié)點(diǎn)為n 的可優(yōu)化環(huán)(a,b)中,當(dāng)采用Dijkstra 松弛條件時(shí),必然有Cost(a,b)+Cost(n,b) p = P{Cost(a,b) 亦即: 若圖G 節(jié)點(diǎn)的平均度為K,那么總的邊數(shù)為NK,去掉傳播樹中的N 條邊,于是可得出可優(yōu)化環(huán)的數(shù)量M=N(K-1)p。 第四步剪除多余分枝過程很明顯時(shí)間復(fù)雜度不超過O(N2)。 綜合以上步驟可得RR 算法的時(shí)間復(fù)雜度上界為2O(N2)+Ο(N2*M)~O(N2*M)。 實(shí)驗(yàn)時(shí)使用的網(wǎng)絡(luò)由Python 中的networkx 庫函數(shù)random_kernel_graph 隨機(jī)生成,調(diào)用方式為nx.random_kernel_graph(n,lambda u,w,z: d *(z- w),lambda u,w,r:r/d+w),其中n 和d 分別要生成的網(wǎng)絡(luò)的節(jié)點(diǎn)數(shù)和平均度,每條邊的權(quán)重為1-10 之間的隨機(jī)數(shù)。 我們比較了不同松弛算法的對(duì)組播樹的影響,見表1。最大長度是指組播樹上最遠(yuǎn)兩個(gè)節(jié)點(diǎn)之間的邊的數(shù)目,這也是衡量組播算法的一個(gè)標(biāo)準(zhǔn),越小意味著組播延遲越低。從表中可以看出,在總代價(jià)方面,采用LMC 的RR 算法效果明顯優(yōu)于采用Dijkstra 的RR 算法,但在最大長度方面卻不如后者。其中可能的原因是LMC 本身在降低代價(jià)方面優(yōu)于Dijkstra。 表1 LMC 和Dijkstra 兩種松弛過程對(duì)RR 算法的影響 我們分析了圖4 所示的網(wǎng)絡(luò)中各種算法所得的總代價(jià),其中OPT 是用窮舉法找到的最佳路徑,可以發(fā)現(xiàn)RR 是最能接近OPT 的算法。 圖4 RR算法與其他算法在特定圖上運(yùn)行結(jié)果對(duì)比 ST 問題是一個(gè)基礎(chǔ)性的課題,其應(yīng)用范圍非常廣泛,對(duì)它進(jìn)行研究也是一種很有啟發(fā)性的工作。近年來隨著人工智能技術(shù)的發(fā)展,有人提出一種觀點(diǎn)認(rèn)為數(shù)據(jù)的重要性大于算法,特別是在神經(jīng)網(wǎng)絡(luò)領(lǐng)域,認(rèn)為只要有了大量的帶標(biāo)注或不帶標(biāo)注的數(shù)據(jù),就可以通過監(jiān)督學(xué)習(xí)或非監(jiān)督學(xué)習(xí)訓(xùn)練出一個(gè)模型來解決相關(guān)問題。但ST 問題目前很難用機(jī)器學(xué)習(xí)方式解決,因?yàn)镾T 問題的規(guī)模的狀態(tài)是不斷變化的,沒有內(nèi)在規(guī)律,也就是說不存在某個(gè)隱藏在數(shù)據(jù)背后的函數(shù)來將問題映射到結(jié)果,很難用一個(gè)模型表達(dá)出來。對(duì)傳統(tǒng)算法的研究與改進(jìn),既有助于促進(jìn)機(jī)器學(xué)習(xí)技術(shù)的發(fā)展,也能提高現(xiàn)有應(yīng)用的效率和水平。4 算法過程
5 時(shí)間復(fù)雜度分析
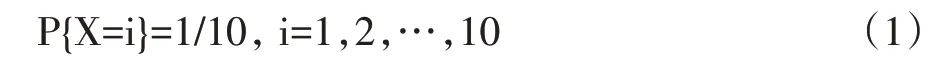
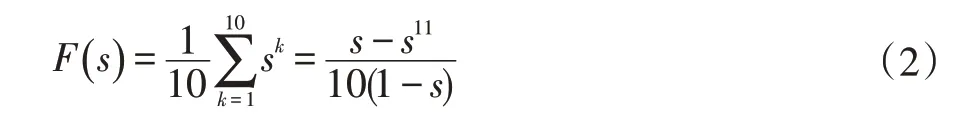
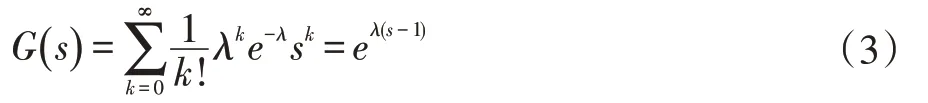

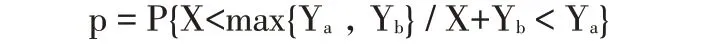
6 實(shí)驗(yàn)與比較
7 結(jié)語

