導(dǎo)管架平臺卡箍修復(fù)的有限元分析

程凱旋， 陳金忠， 楊樹耕

(天津大學(xué) a.建筑工程學(xué)院； b.水利與安全國家重點實驗室， 天津 300072)

0 引 言

據(jù)統(tǒng)計，全球現(xiàn)役的導(dǎo)管架平臺中，大約有1/3已經(jīng)使用15年以上[1]，這些老齡平臺的許多構(gòu)件已出現(xiàn)不同程度的疲勞裂紋，結(jié)構(gòu)老化和損傷嚴(yán)重，平臺在這種狀態(tài)下無法繼續(xù)服役。由于海洋平臺建造周期長、投資大，因此選擇對損傷后的平臺進行修復(fù)是一種更經(jīng)濟的手段。為此，需要對損傷修復(fù)后的平臺結(jié)構(gòu)進行強度校核，以驗證現(xiàn)有的修復(fù)形式是否可以滿足使用要求。

目前對損傷構(gòu)件的修復(fù)主要使用卡箍法。卡箍法是用套筒從外部套住受損構(gòu)件的損傷部位，通過各瓣邊緣的螺栓連接并緊固，使套筒卡在受損構(gòu)件上，通過兩者之間的摩擦力或剪力鍵來傳力，以提高受損部位的強度。卡箍法有多種形式，如機械卡箍、灌漿卡箍、壓力卡箍等。

有學(xué)者已經(jīng)在卡箍法的有限元分析方面取得了一些成果。多數(shù)學(xué)者的研究工作集中于研究卡箍修復(fù)后的極限承載力方面。龔順風(fēng)等[2]在模型試驗的基礎(chǔ)上使用非線性有限元程序?qū)型灌漿卡箍節(jié)點的極限承載能力進行計算，得出其軸向拉壓和承受面內(nèi)彎矩的極限承載力。金偉良等[3]使用ANSYS軟件建立有凹陷的直管模型和使用灌漿卡箍修復(fù)后的模型，使用BRICK 45和SHELL 143單元對構(gòu)件進行剖分，通過比較兩者，研究修復(fù)效果和極限承載力的情況。徐爽等[4]針對灌漿卡箍維修加固方法，選用ANSYS的分層單元模擬管節(jié)點處維修加固前后的應(yīng)力狀態(tài)變化，并利用局部模型嵌入整體模型的方法進行分析計算，驗證修復(fù)效果。宋朝霞等[5]使用SACS軟件建立使用卡箍連接的臨時取樣平臺模型，驗證其是否滿足規(guī)范要求。

本文對機械卡箍修復(fù)方法進行有限元分析，研究其在ANSYS軟件中的模擬方法并對其修復(fù)效果進行驗證，并研究3個典型節(jié)點的最小修復(fù)長度和平臺中單個節(jié)點修復(fù)后的影響。

1 ANSYS中卡箍修復(fù)模擬方法

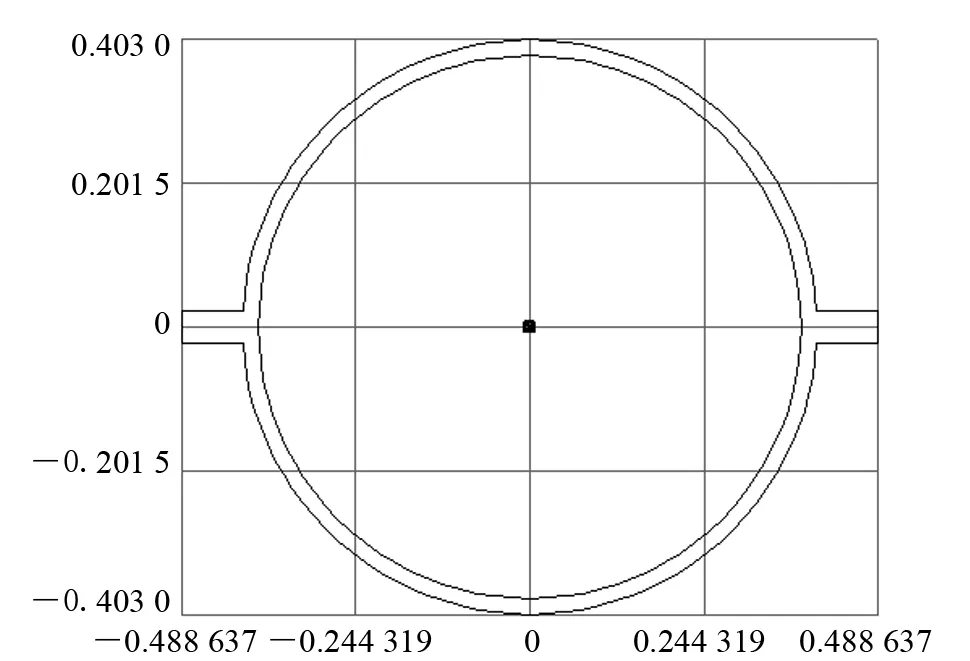
圖1 卡箍截面形式

為了研究受損節(jié)點卡箍的模擬方法，使用ANSYS軟件對導(dǎo)管架中3種典型的結(jié)構(gòu)形式，即T型節(jié)點、K型節(jié)點和直管跨中節(jié)點的修復(fù)卡箍進行模擬。管體模型均為軸線模型，使用PIPE 288單元，在損傷處設(shè)置兩個獨立的節(jié)點模擬損傷處全部斷開，在卡箍模型的模擬中使用BEAM 188單元的自定義截面功能。模型中使用的卡箍均為兩瓣式卡箍，通過各瓣邊緣的螺栓連接緊固成為一體并擰緊卡在受損部位上。為了提高計算效率并簡化模型，將卡箍螺栓連接部分簡化為直接連接，即假定卡箍的兩瓣為一個整體。首先，在ANSYS中繪制如圖1所示的卡箍截面形式，將該面設(shè)置為PLANE 82單元，并進行網(wǎng)格劃分，將結(jié)果輸出為.sect文件。然后，手動定義模擬卡箍的BEAM 188單元，將上一步得到的.sect文件設(shè)置為單元的橫截面形狀。最后，在管體節(jié)點上直接創(chuàng)建卡箍單元，使兩者聯(lián)系在一起，以滿足連續(xù)性要求和載荷傳遞要求。

節(jié)點模型如圖2所示。

圖2 3種關(guān)節(jié)點形式

(1) T型節(jié)點：管體尺寸分別為φ762 mm×13 mm和φ508 mm×13 mm，管長分別為12 m和2.582 m；斷裂處為兩管節(jié)點焊縫，長度為100 mm。使用卡箍壁厚為19 mm。

(2) K型節(jié)點：管體尺寸分別為φ610 mm×19 mm和φ610 mm×13 mm，直邊管長為19.5 m，兩斜撐管長均為15.286 m；斷裂處為斜撐右側(cè)管節(jié)點焊縫，長度為100 mm。使用卡箍壁厚為22 mm。

(3) 直管跨中節(jié)點：管體尺寸為φ762 mm×19 mm，管長為16.2 m；斷裂處位于直管跨中位置，長度為100 mm。使用卡箍壁厚為22 mm。

以上節(jié)點模型使用材料為鋼材，設(shè)定彈性模量為2.1×108kPa，泊松比為0.3。

建立以上3種節(jié)點模型后進行加載求解，驗證模型是否達到修復(fù)目的，并研究每個模型達到修復(fù)效果的最小卡箍長度。

2 局部模型中最小卡箍長度

建立完好的節(jié)點模型和卡箍修復(fù)后的節(jié)點模型，在相同位置施加單位力和單位彎矩，求解后驗證修復(fù)后的結(jié)構(gòu)能否達到載荷傳遞和保證修復(fù)后結(jié)構(gòu)連續(xù)性的目的。分別調(diào)整3種節(jié)點模型的卡箍長度，研究不同卡箍長度對修復(fù)效果的影響。針對不同卡箍長度，比較修復(fù)后損傷附近的最大von Mises應(yīng)力相對于完好模型中該處應(yīng)力的變化程度，即該處的應(yīng)力變化率。應(yīng)力變化率的絕對值越大表示應(yīng)力變化越劇烈，使用卡箍帶來了額外的強度，應(yīng)力變化越劇烈說明額外強度越大，修復(fù)效果越明顯。

2.1 T型節(jié)點卡箍修復(fù)

圖3 拉力作用時T型節(jié)點水平段不同 卡箍長度時的應(yīng)力變化率

在T型節(jié)點模型的豎直管端部施加軸向單位拉力，調(diào)整卡箍長度分別進行計算。豎直段卡箍長度固定為0.4 m，調(diào)整水平段卡箍長度，加載求解后所得數(shù)據(jù)如圖3所示。可以看出，上述卡箍均能滿足修復(fù)要求。水平段卡箍長度每改變管徑的0.25倍，應(yīng)力變化率的增量約為1.22%，可近似認(rèn)為應(yīng)力大小隨卡箍長度線性變化。

在豎直管端部施加軸向單位拉力，水平段卡箍長度固定為1.4 m，調(diào)整豎直段卡箍長度，求解后發(fā)現(xiàn)豎直段卡箍的變化對軸向載荷的承載力基本沒有影響。可以看出，對于受軸向載荷的修復(fù)節(jié)點，水平段卡箍產(chǎn)生的修復(fù)效果更為明顯，豎直段卡箍長度只需考慮構(gòu)造要求即可。在實際應(yīng)用中，在進行軸向載荷下T型節(jié)點修復(fù)時，增加水平卡箍長度或者增加使用卡箍的壁厚是提高修復(fù)效果的有效方法。

在豎直管端施加單位彎矩Mz=1 kN·m，豎直管段卡箍長度固定為0.6 m，調(diào)整水平卡箍長度，加載求解后對損傷附近的最大應(yīng)力與完好模型中該處應(yīng)力進行比較。卡箍長度與應(yīng)力變化率的關(guān)系如圖4(a)所示。可以看出，在施加彎矩情況下，改變水平管段卡箍長度對承載力的影響較小。

在豎直管端施加單位彎矩Mz=1 kN·m，水平直管段卡箍長度固定為1.4 m，調(diào)整豎直卡箍長度分別進行計算，加載求解后對損傷附近的最大應(yīng)力與完好模型中該處應(yīng)力進行比較。卡箍長度與應(yīng)力變化率的關(guān)系如圖4(b)所示。可以看出，豎直卡箍長度增長至管徑兩倍后，隨著卡箍長度增加，修復(fù)處應(yīng)力增大。這是因為卡箍過長，使得卡箍邊緣距離加載處較近。在此種情況下，卡箍會將彎矩載荷更多地傳遞至損傷處，反而對修復(fù)效果不利。

在實際應(yīng)用中，如果受彎矩作用的T型節(jié)點的損傷管段長度較短，應(yīng)避免卡箍與載荷集中處距離過小，此時增加卡箍長度將對修復(fù)效果不利，應(yīng)考慮增加水平卡箍長度或增大卡箍壁厚提高修復(fù)效果。

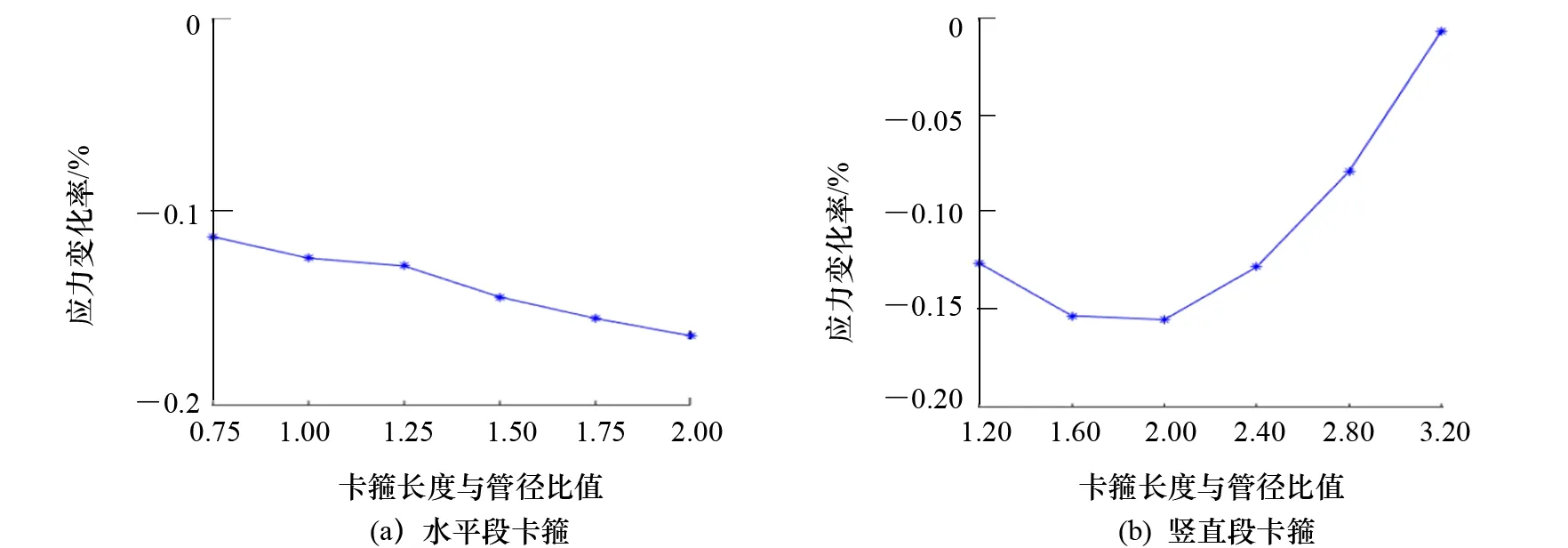
圖4 彎矩作用時T型節(jié)點水平段及豎直段不同卡箍長度的應(yīng)力變化率

2.2 K型節(jié)點卡箍修復(fù)

在K型節(jié)點的豎直管端部施加軸向單位拉力，調(diào)整卡箍長度進行比較計算。斜向卡箍長度固定為0.7 m，調(diào)整水平段卡箍長度，加載求解后，將損傷附近的最大von Mises應(yīng)力與完好模型中該處von Mises應(yīng)力進行比較。卡箍長度與應(yīng)力變化率的關(guān)系如圖5所示。可以看出，當(dāng)水平卡箍長度為管徑的2.6倍時不能滿足修復(fù)要求。隨著水平卡箍長度的增加，修復(fù)管處應(yīng)力逐漸變小，且變化率逐漸增大。這說明K型節(jié)點的水平卡箍長度增加對損傷修復(fù)效果是有益的，且隨著卡箍的加長，增加卡箍長度的額外修復(fù)效果在增強。

在豎直管端部施加軸向單位拉力，調(diào)整斜向卡箍長度進行比較計算。固定水平段卡箍長度為管徑的4倍，調(diào)整斜向卡箍長度，加載求解后，將損傷附近的最大von Mises應(yīng)力與完好模型中該處von Mises應(yīng)力進行比較，卡箍長度與應(yīng)力變化率的關(guān)系如圖6所示。可以看出，當(dāng)斜向卡箍長度增大至管徑的2.1倍時不能滿足修復(fù)要求。隨著斜向卡箍長度的增加，修復(fù)管處應(yīng)力逐漸變大，變化率逐漸減小。這說明K型節(jié)點的斜向卡箍長度增加對損傷修復(fù)效果的提升不顯著。

圖5 拉力作用時K型節(jié)點水平段不同卡箍長度時的應(yīng)力變化率

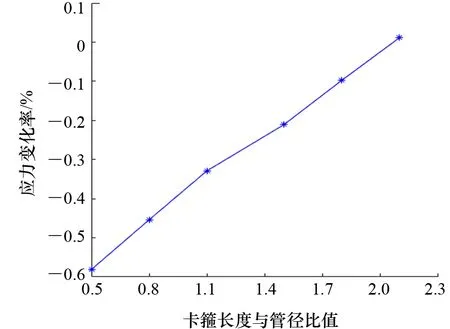
圖6 拉力作用時K型節(jié)點斜向不同卡箍長度時的應(yīng)力變化率

在實際應(yīng)用過程中，受軸向力的K型節(jié)點斜向卡箍不宜過長，增加卡箍水平長度或者增大卡箍壁厚才是提高修復(fù)效果的有效方法。

在豎直管端施加單位彎矩Mz=1 kN·m，斜向管段卡箍長度固定為管徑的1.1倍，調(diào)整水平卡箍長度進行計算，加載求解后，將損傷附近的最大von Mises應(yīng)力與完好模型中該處von Mises應(yīng)力進行比較，卡箍長度與應(yīng)力變化率的關(guān)系如圖7所示。可以看出，上述水平卡箍長度都可以滿足修復(fù)需要。但是隨著水平卡箍的加長，最大應(yīng)力增加，增長率降低，說明在彎矩作用下，水平卡箍長度增加對修復(fù)效果的提升不顯著。在實際應(yīng)用中，應(yīng)注意合理選擇水平卡箍長度，以免浪費材料和損失修復(fù)效果。

水平段卡箍長度固定為管徑的4倍，調(diào)整斜向卡箍長度，加載求解后，將損傷附近的最大von Mises應(yīng)力與完好模型中該處von Mises應(yīng)力進行比較，卡箍長度和應(yīng)力變化率的關(guān)系如8所示。可以看出，上述長度的斜向卡箍都可以滿足修復(fù)需要。隨著斜向卡箍的加長，最大應(yīng)力減小，且變化率在增大，說明在彎矩作用下，斜向卡箍長度增加對修復(fù)效果的提升有利，且隨著卡箍的加長，增加卡箍長度的額外修復(fù)效果在增強。

圖7 彎矩作用時K型節(jié)點水平向不同卡箍長度時的應(yīng)力變化率

圖8 彎矩作用時K型節(jié)點斜向不同卡箍長度時的應(yīng)力變化率

2.3 直管跨中節(jié)點卡箍修復(fù)

在直管跨中節(jié)點模型的兩端分別單獨施加軸力和彎矩。模擬結(jié)果顯示，在軸力和彎矩分別作用下，不同長度的22 mm壁厚卡箍均能達到修復(fù)目的，且增加卡箍長度應(yīng)力基本不發(fā)生變化，說明在此種情況下較短的卡箍即可達到修復(fù)目的，在實際使用中只需考慮構(gòu)造要求即可。

通過上述分析可以看出，此種方法可以成功模擬實際平臺卡箍修復(fù)后的情形。計算發(fā)現(xiàn)，在對直管跨中節(jié)點進行修復(fù)時，0.65倍管徑長度的卡箍即可達到有效的修復(fù)目的。修復(fù)T型節(jié)點時，改變豎直段卡箍長度對軸向載荷作用下節(jié)點的修復(fù)效果改變不明顯，水平段卡箍長度為0.75倍管徑時即可達到修復(fù)效果。修復(fù)K型節(jié)點時，在軸向載荷為主要載荷情況下，斜向卡箍長度不應(yīng)超過管徑的2倍，水平段卡箍長度應(yīng)大于管徑的3倍，但過長的水平卡箍不利于達到修復(fù)效果并且浪費材料。

3 整體模型中單個節(jié)點卡箍修復(fù)后對結(jié)構(gòu)的影響

圖9 導(dǎo)管架模型示例

使用ANSYS建立完好的整體導(dǎo)管架模型，如圖9所示。損傷模型主體與完好模型相同，假設(shè)損傷處為水線面附近X型節(jié)點的焊縫斷裂，損傷處單根構(gòu)件長度為9.591 m，管材尺寸為φ941 mm×22 mm，假設(shè)損傷處為完全斷裂，斷裂長度為100 mm。使用卡箍為鋼制卡箍，壁厚為24 mm。設(shè)定單向卡箍長度為管徑的1.5倍，模型如圖10所示。在兩個模型的導(dǎo)管架頂端的4個節(jié)點施加豎直向下的集中力5 000 kN，模擬上部組塊對導(dǎo)管架的載荷作用。添加海洋環(huán)境載荷，設(shè)定海水密度為1 030 kg/m3，水深為79.4 m，波高為8 m，周期為10 s，拖曳力系數(shù)CD=0.5，慣性力系數(shù)CM=2，并進行波浪搜索確定最大波浪力相位角。

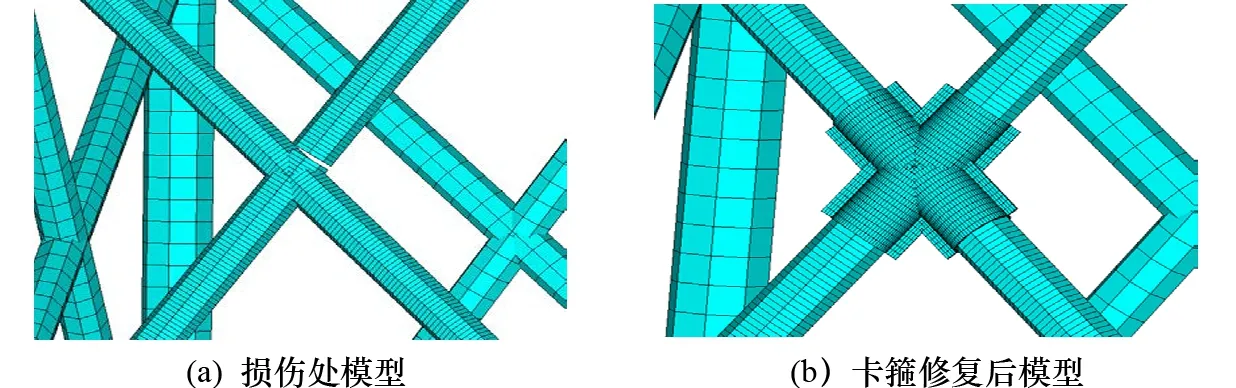
圖10 損傷處及卡箍修復(fù)示例

對加載后的整體模型進行波浪搜索。設(shè)定波浪為x軸正向入射、對角線入射(即與x軸夾角為48.6°)和y軸正向入射，波浪搜索后求得最大波浪力的相位角分別為109°、110°和110°。分別對完好模型和修復(fù)后模型求解，通過后處理得到模型的相關(guān)位移和應(yīng)力數(shù)據(jù)，并按《海上固定平臺入級與建造規(guī)范》[6]校核最大軸向應(yīng)力。選用的規(guī)范公式為

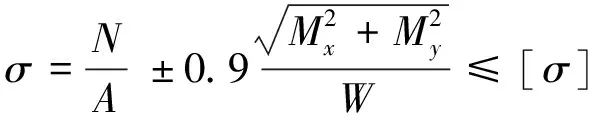
(1)

式中：σ為軸向應(yīng)力，MPa；N為計算截面的軸向力，N；A為計算截面的彎矩,N·mm；Mx和My為計算截面分別繞x軸和y軸的彎矩；W為圓管截面的剖面模數(shù)。

將兩個模型在3種波浪情況下的數(shù)據(jù)匯總?cè)绫?所示。

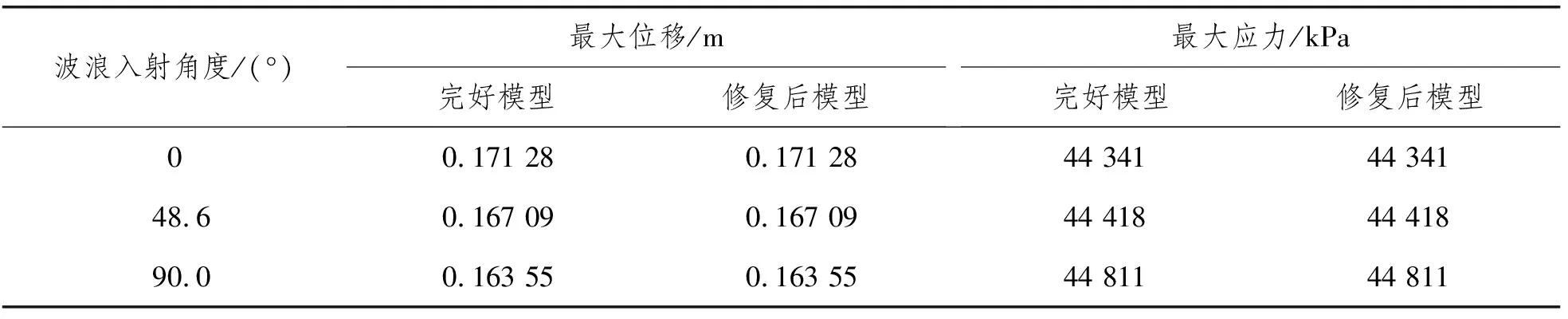
表1 整體最大應(yīng)力和最大位移對比表

從表1可以看出，完整模型按規(guī)范校核的最大應(yīng)力和最大位移的數(shù)值均在規(guī)定范圍內(nèi)，說明使用的模型是合理的。通過兩個模型的比較可以看出，只對單一節(jié)點進行卡箍修復(fù)對整體結(jié)構(gòu)的最大應(yīng)力和最大位移沒有影響。

比較修復(fù)節(jié)點及該節(jié)點相鄰桿件的局部應(yīng)力與位移，將不同波浪入射角下的局部最大von Mises應(yīng)力和最大位移匯總?cè)绫?所示。

表2 局部最大應(yīng)力和最大位移對比表

從表2可以看出，在3種不同的波浪入射角條件下，1.5倍管徑長度的卡箍均能達到修復(fù)效果。修復(fù)后節(jié)點附近最大von Mises應(yīng)力下降3%左右，最大位移增加值均在1 cm以內(nèi)。同時，該修復(fù)措施對結(jié)構(gòu)整體位移和靜力強度沒有影響。因此，可以認(rèn)為在此模型中，應(yīng)用1.5倍管徑長度的卡箍可以滿足此模型的修復(fù)要求。

4 結(jié) 論

提出了在ANSYS中設(shè)置獨立節(jié)點并使用BEAM 188單元的自定義截面功能創(chuàng)建卡箍單元模擬卡箍修復(fù)后結(jié)構(gòu)的方法。進一步應(yīng)用此方法對3種導(dǎo)管架平臺中典型節(jié)點的卡箍修復(fù)后的結(jié)構(gòu)進行了局部結(jié)構(gòu)靜力分析，找到了修復(fù)3種節(jié)點的最小卡箍長度。最后，應(yīng)用此方法研究導(dǎo)管架整體模型的單個節(jié)點修復(fù)后對整體結(jié)構(gòu)和該節(jié)點的影響。此次研究過程成功實現(xiàn)了對導(dǎo)管架平臺卡箍修復(fù)后結(jié)構(gòu)的數(shù)值模擬，在此基礎(chǔ)上進一步研究了不同形式的卡箍以及卡箍長度對修復(fù)效果的影響，所取得的研究成果可應(yīng)用于局部損壞平臺的修復(fù)效果評估。