臂式高空作業平臺裝配線及物料配送設計*

黃向明 韓 竹 劉國良 尹人奇

(1.湖南大學 機械與運載工程學院 長沙410082；2.湖南星邦重工有限公司 長沙410060)

為了保障工人在高處作業的安全性，高空作業平臺開始取代傳統落后的高空作業方式[1]。高空作業平臺屬于工程機械行業，是用來進行高空作業的專用設備[2]。目前高空作業平臺被廣泛應用到工程建設、工業安裝和設備檢修等行業[3]。使用工程機械產品保證高空作業的安全，從而更好地拓展新興工程機械市場。

近幾年來，高空作業平臺的產銷量持續增加，發展狀況越來越好，市場需求大幅度上升[4]。然而目前某企業臂式高空作業平臺一直采取定點放置裝配，周期長，質量得不到保障，生產效率低，物流配送不及時，產量達不到預期效果，不能保障產能需求。目前對于工程機械裝配線的研究主要在物流配送路徑方面，Tao[5]等對滿足最大載重量的配送車輛路徑隨機的問題提出了分散搜索的辦法，采用機會約束對模型進行求解。Narges[6]等根據生產需求、生產批量和調度車輛的前提條件構建配送車輛路徑優化問題。王楠[7]等研究廠內的物料配送，選取混合時間窗的約束條件，在物料到達的時間上進行限制。胡詳培[8]根據字典序的方法，對配送車輛路徑的優化進行需求變動的目標函數規劃和求解，求解該項目的總承包成本最小化。楊斯淇[9]等則是根據車間的實際制造生產的現狀和問題，構造一個有容量限制要求的物料配送車輛路徑優化函數。

本文針對某企業目前的裝配現狀，結合臂式高空作業平臺的裝配工藝要求，設計出臂式高空作業平臺裝配線，并對大件物料的配送路徑進行研究，從而提升產能，保證物流配送的有效性和穩定性，與此同時利用仿真軟件驗證設計的可行性。

1 臂式高空作業平臺裝配線設計

1.1 臂式高空作業平臺裝配工藝流程規劃

臂式高空作業平臺主要是行走、轉臺、臂架和平臺四個部分的裝配，如圖1所示。

圖1 臂式高空作業平臺裝配流程圖

1.1.1 標準作業時間測量

根據臂式高空作業平臺裝配工藝，將其分為三部分：第一部分(1~15工序)是行走安裝；第二部分(16~38工序)是臂架安裝前；第三部分(39~55工序)是臂架安裝后。

采取秒表測時測量一個標準工人裝配的時間，觀測10次，寬放系數為1.1，計算平均值得到各工序的標準加工時間如表1、表2和表3所示。

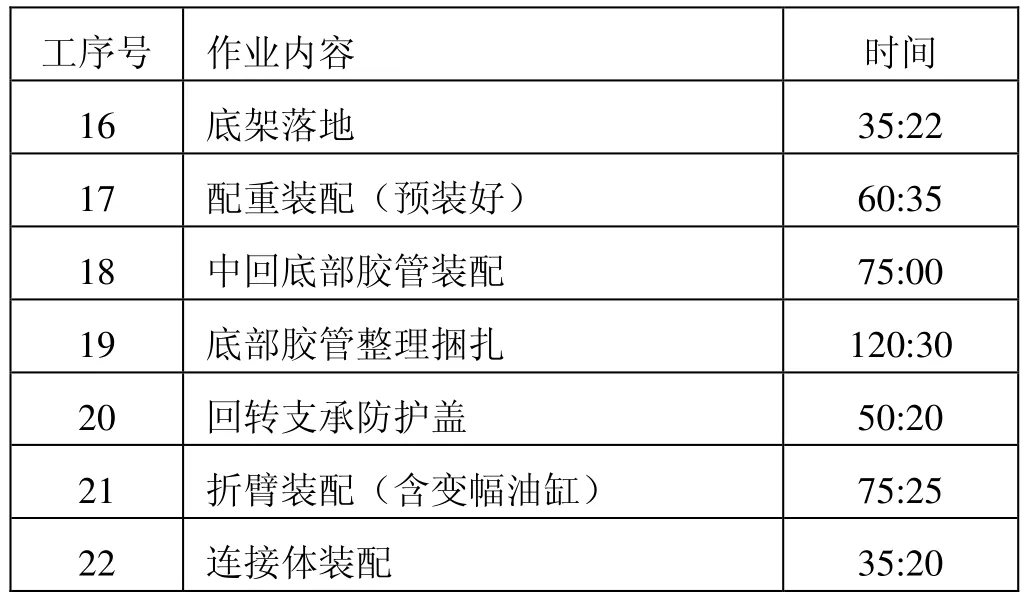
表2 臂架安裝前各工序的標準加工時間 (min)

接上表

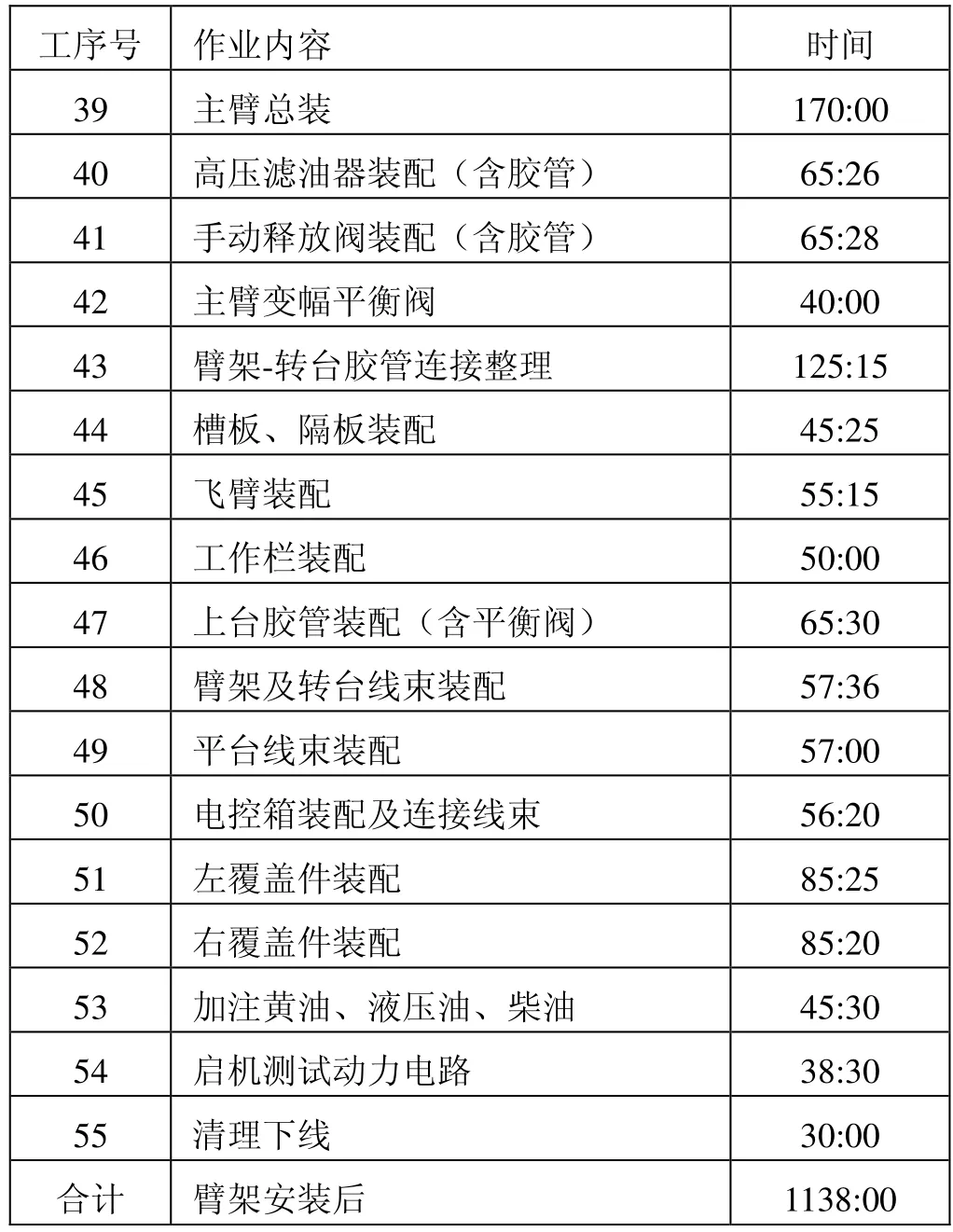
表3 臂架安裝后各工序的標準加工時間 (min)

1.1.2 生產節拍確定

該企業工作時間是8小時，在裝配生產過程中會產生不合格產品和廢品，公式為：

式中：F效指有效工作時間，F制指制度工作時間，K指時間利用系數，K=0.85，因此臂式高空作業平臺F效=459min。

裝配線生產節拍指裝配線完成兩個一樣產品的時間間隔。生產節拍計算公式為：

式中：R指的是裝配線生產節拍時間；Q指的是產品的產量，因此R=F效÷Q=459÷8÷26≈57.38=57min/臺。

由于該產品品種多，其質量和體積大，節拍時間長，采用移動間斷裝配線，強制節拍，工人和設備器具固定在各工位[5-6]。

1.1.3 工人數量和工位數計算

需要的工人數量，公式為：

式中：n為工人數量，T為標準作業時間，M為日產量。

需要的工位數，公式為：

式中：N為工位的數量，取大于或等于數值的最小整數，φ為工位人員密度，取3。

通過計算得數據如表4所示。

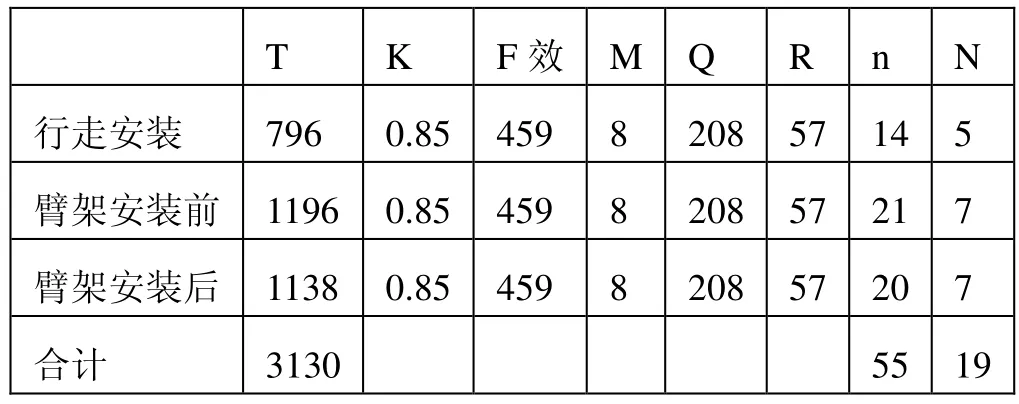
表4 工人和工位的數量確定

1.1.4 工位工序內容劃分

按照節拍時間57min和工位數19個，劃分各工位的具體工序內容，如表5所示。

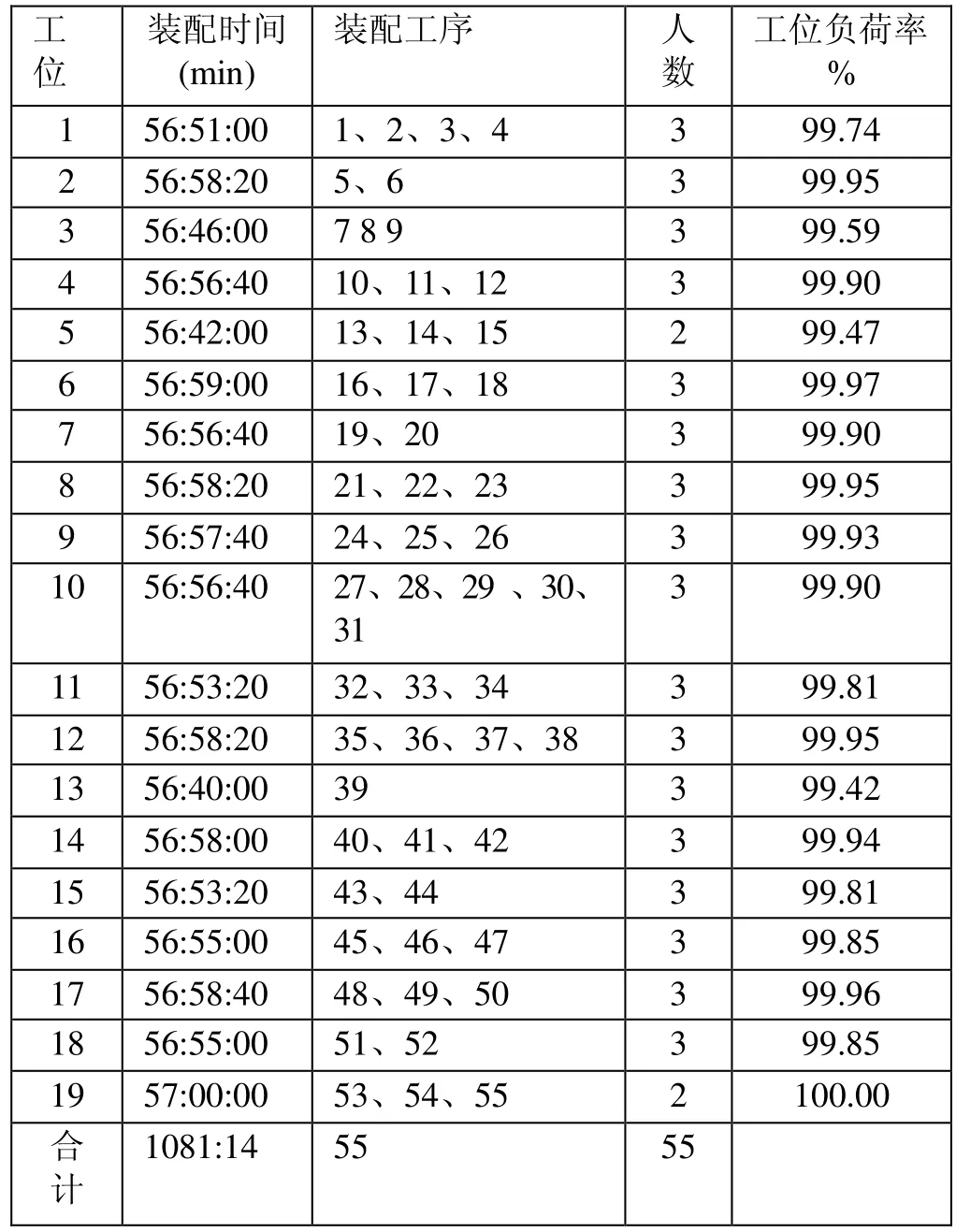
表5 各工位的工序、工人和裝配時間的數據匯總

1.2 臂式高空作業平臺裝配線布局

臂式高空作業平臺裝配線包含19個工位，總長為100.5 m，運輸方式選擇地推鏈與板鏈輸送線。地推鏈為27.5 m，產品布置方向為縱向布置，負責行走安裝的5個工位，底架放置到地拖鏈的支撐上，安裝支腿、減速機、連接盤、馬達、轉向機構和輪胎等；當行走安裝完成，從地推鏈吊裝至雙板鏈線上，將產品由豎向擺放變為橫向布置，設置吊轉平臺，總長為5.8 m；雙板鏈為67.2 m，產品布置方向為橫向布置，負責臂架安裝前后的14個工位，主要進行液壓、電氣件、臂架和操作欄的裝配。臂式高空作業平臺裝配線的面積是100.5×7.1 m2，上線區面積是15.3×6.8 m2，下線區面積是15.3×6.6 m2，線邊物料倉的面積是100.5×8.3 m2，物料倉庫面積是41.0×9.2 m2。臂式高空作業平臺裝配線平面和現場布置如圖2和圖3所示。

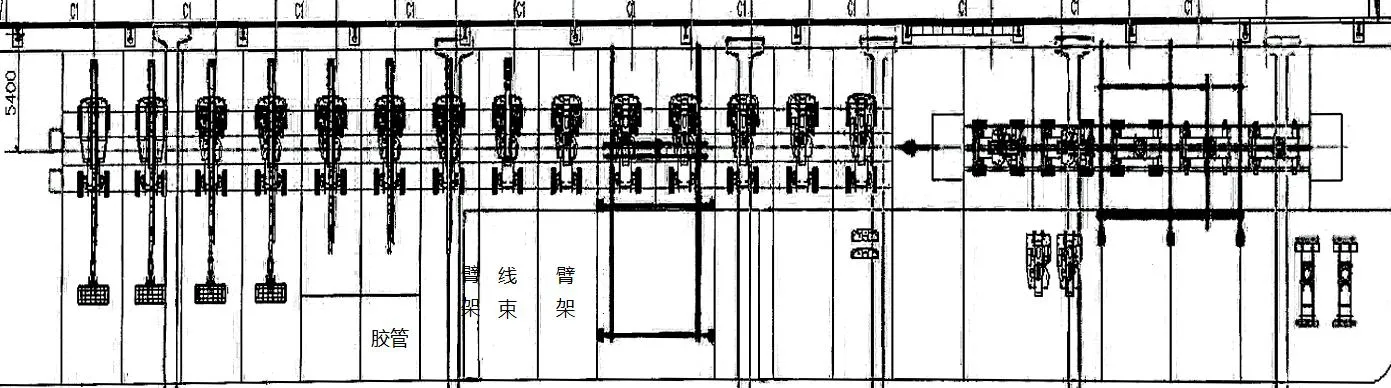
圖2 臂式高空作業平臺裝配線的平面布置圖

圖3 裝配線及物料區布置圖

2 超大件和標準件物料配送設計

2.1 裝配線物料配送分析

2.1.1 大件物料配送數量的確定

根據物料的體積和質量劃分[7]，將臂式高空作業平臺物料分為標準件、超大件和SPS件，其中SPS物料的體積和質量適中。臂式高空作業平臺的物料劃分如表6所示。

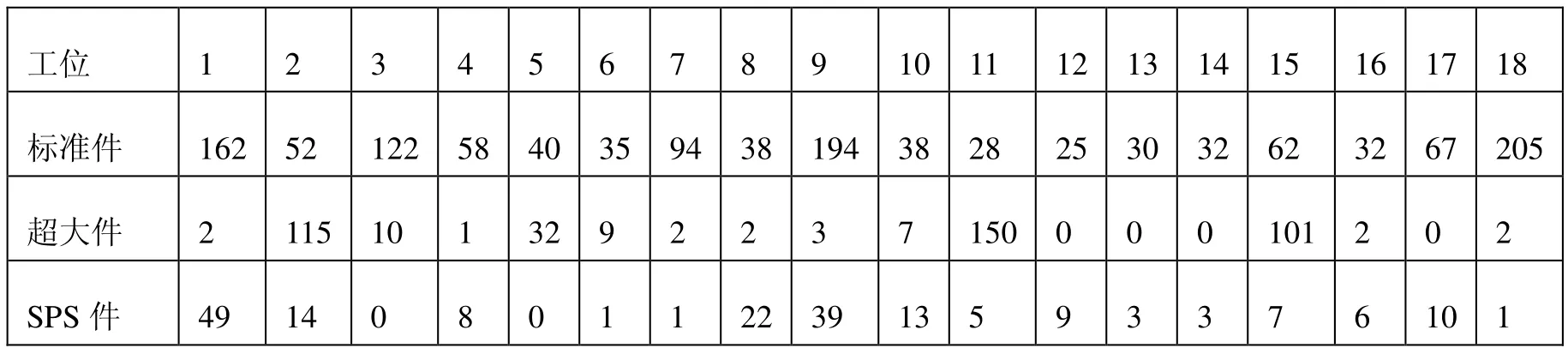
表6 物料分類表 (件)

2.1.2 配送車輛的數量確定

確定臂式高空作業平臺大件物料的配送車輛的需求數量，其計算公式如下：

式中：a的取值范圍是（0,1），取a=0.85，由表6可知大件物料總需求量∑qi=1341個，最大載貨量Q=500個，［∑qi/aQ］表示的是將符號里的值向下取整，可計算出配送車輛的數量h為4輛，設置配送車輛行駛速度為0.75 m/s。

2.1.3 各工位坐標和物料需求時間的確定

以臂式高空作業平臺的物料區左下角的端點作為坐標原點，創建直角坐標系，所有區域的坐標位置均以其中心點的位置來確定[8]。研究對象是在8個小時內配送的物料，各個工位的詳細數據如表7所示。

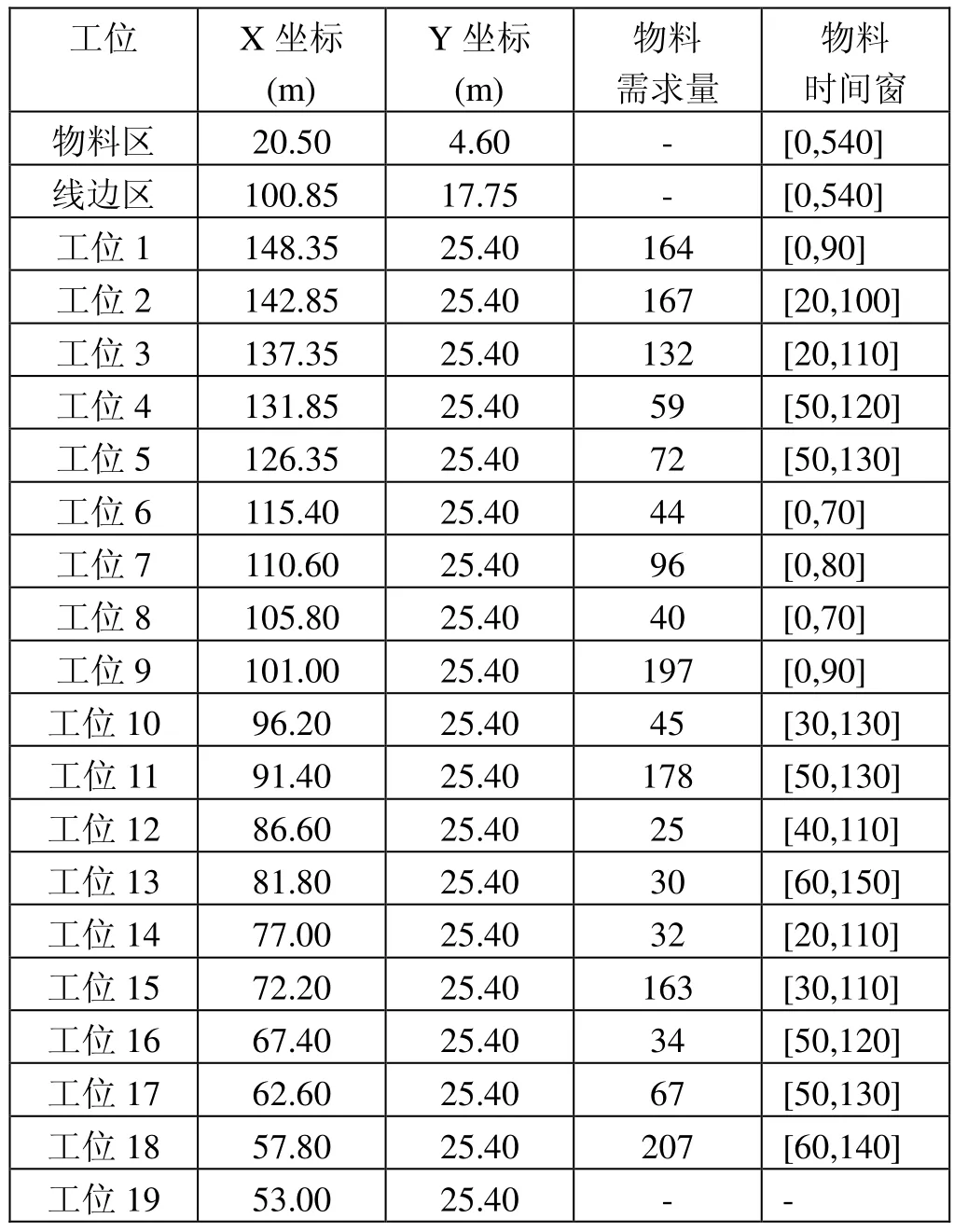
表7 各工位坐標、物料需求量和時間窗信息匯總表

2.2 配送車輛路徑優化模型建立

2.2.1 問題描述

為便于分析問題，做了如下建模假設[9]：

（1）每工位只由一輛配送車輛配送；

（2）所有配送車輛從配送點出發最后必須返回配送點；

（3）配送車輛配送物料的總量不超過其最大載重量；

（4）配送點有足夠配送車輛配送；

（5）配送車輛的速度都是勻速行駛；

（6）不考慮配送車輛最大行駛距離；

（7）不考慮物料裝載時間和卸料時間；

（8）配送車輛的型號、最大載重量和行駛的速度都是一樣的。

2.2.2 目標函數

目標函數為總配送成本最小化：

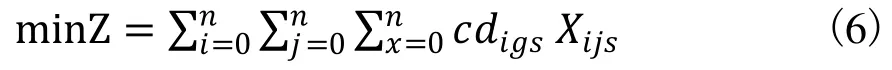
式中：Z表示總配送成本，minZ表示總配送成本最小化；n表示裝配線的工位數，因第19個工位是進行車輛下線前的調試工作，沒有物料需要進行配送，n取值18個工位，將1到18個工位編號為1-18，0是物料區的編號，i，j指的是工位i和工位j，所以i=0，1，2，...，n，j=0，1，2，...，n；h表示臂式高空作業平臺裝配線的物料配送的車輛總數，s指的是車輛，所以s=1，2，...，h；c指的是單位距離內配送車輛配送物料的單位成本；Xijs是一個0~1變量，表示如果配送車輛s從工位i行駛到工位j，那么Xijs的值是1，如果配送車輛s沒有從工位i行駛到工位j，則Xijs的值是0；dijs表示配送車輛s從工位i行駛到工位j的距離。

2.2.3 約束條件

必須滿足下列的約束條件：

式中：Yis是0-1變量，若工位i是由配送車輛s配送，那么Yis的值是1，若工位i不是由配送車輛s配送，那么Yis的值是0。

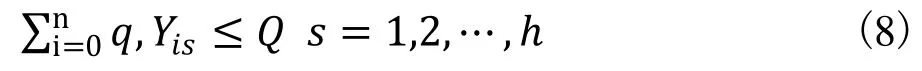
式中：qi指第i個工位需要的物料數量；Q指每個車輛的最大載重量；式子指某輛配送車輛s裝載的若干個工位的物料總需求量不會超過這輛配送車輛的最大載重量。

每個工位只允許同一輛配送車輛對其進行配送物料如下式：

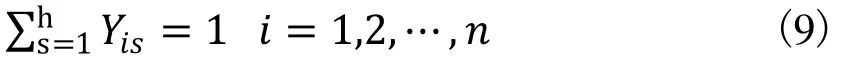
配送車輛都會返回到配送點如式（10）。

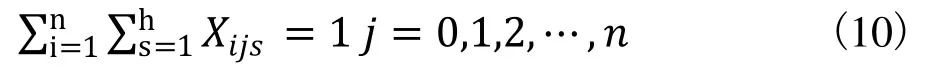
2.3 遺傳算法求解模型

2.2.1 求解步驟

（1）進行控制參數的選擇和設定，主要針對種群規模N和交叉概率Pc，變異概率P?和終止最大迭代次數Gen等重要參數；

（2）采用自然編碼對各工位進行編碼，隨機生成初始染色體種群；

（3）計算每個染色體適應度函數占種群總染色體適應度函數的比例，根據輪盤賭法選擇比例較大的染色體進行選擇和復制；

（5）根據Pc，在N中隨機選N×Pc個染色體進行交叉操作，選取部分映射交叉；

（6）根據P?，在N中隨機選N×Pc個染色體進行變異操作，選取反轉變異；

（7）將經過選擇、交叉和變異操作得到的染色體代入終止條件進行計算和驗證，滿足終止條件便停止迭代，反之繼續迭代；

（8）當算法終止迭代后，得到最優的染色體解，根據已知條件求出目標問題的最優路徑和最小配送總成本。

2.2.2 求解結果對比分析

設置N=50，Pc=0.8，P?=0.2，Gen=200，c=2，Q=500。取適應度函數為目標函數的倒數，經過200次的迭代運算，得出每一代適應度的平均值，遺傳算法在第158代達到最優解，如圖5所示。

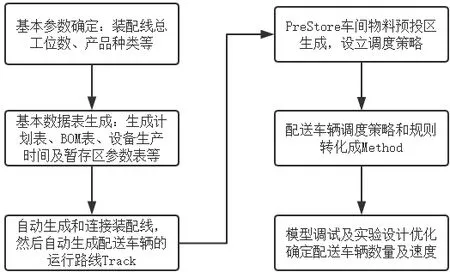
圖5 遺傳算法迭代收斂

此時遺傳算法迭代得到最優染色體為：0-1-2-3-14-0-4-5-6-7-8-0-9-10-11-12-13-0-15-16-17-18-0。染色體對應的工位配送順序如表8所示，遺傳算法優化后各配送車輛的求解結果如表9所示。

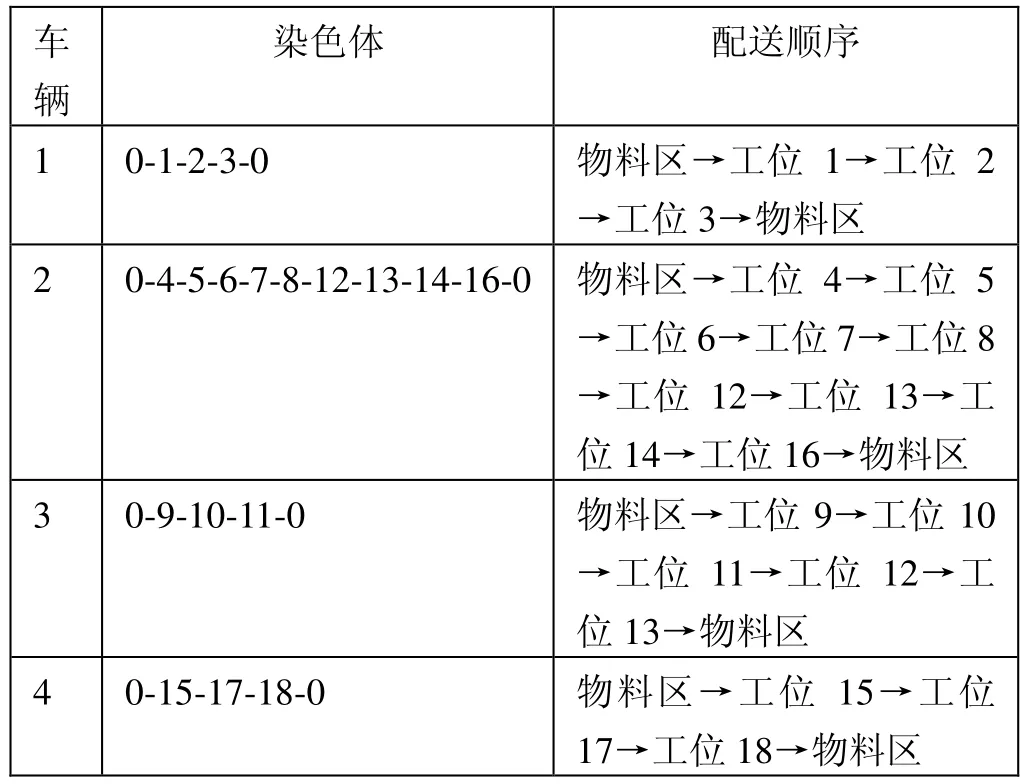
表8 遺傳算法得出的最優染色體解

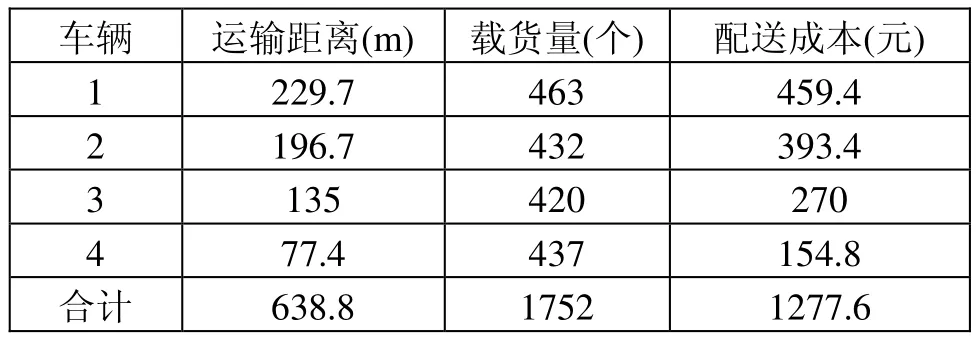
表9 算法優化后各配送車輛的求解結果

臂式高空作業平臺裝配線的大件物料進行遺傳算法求解時生成的初始染色體是：0-1-5-9-0-2-6-10-13-15-0-3-7-11-14-0-4-8-12-16-17-18-0。

將遺傳算法求得最優解的優化結果與裝配線初始染色體配送路徑的數據結果進行比較和分析，通過整理匯總得到下表，如表10所示。

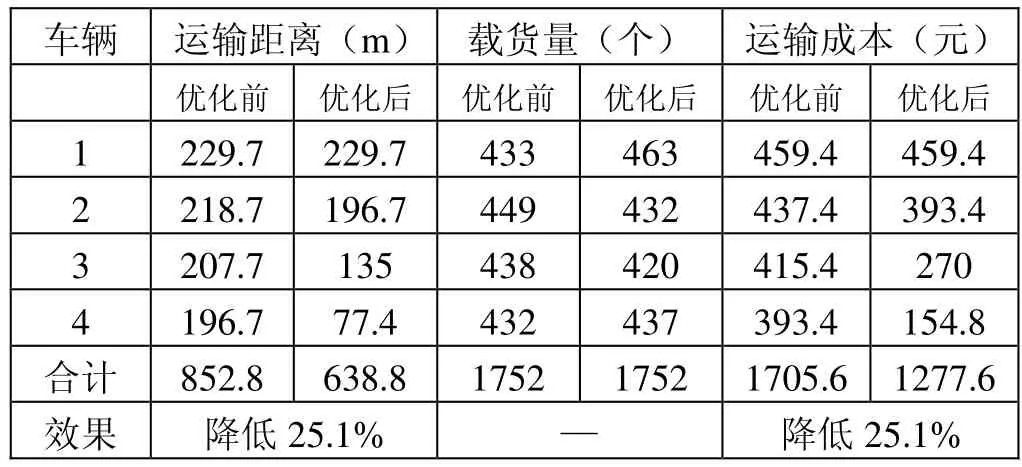
表10 優化前后配送數據匯總

通過對遺傳算法求解優化前后的配送數據進行對比和分析，遵循最大載貨量的條件得到的優化后的總配送成本由1705.6元減少到1277.6元，比率減少25.1%，驗證了本文車輛路徑優化模型的可行性。

3 基于eM-plant的裝配線仿真

3.1 仿真建模基本框架

模型建立的流程如圖6所示。

圖6 臂式高空作業平臺裝配線仿真建模流程圖

由圖可知，首先確定基本參數如裝配線總工位數等，然后生成基本數據表如生產計劃表和暫存區參數表等，接著通過代碼自動生成臂式高空作業平臺裝配線，確定配送車輛的運行路線，驗證裝配線和物流配送設計方案的可行性，最后進行因子設計試驗確定配送車輛的數量及速度。

3.2 裝配線仿真模型建立

利用eM-plant軟件對臂式高空作業平臺裝配線進行仿真建模[10]。依次創建調用裝配線運行的各個模塊代碼，仿真將自動生成由19個工位和線邊暫存區組成的裝配線模型，以及配送車輛的軌跡路線，如圖7所示。

臂式高空作業平臺裝配線的仿真模型通過EventController運行，得出整個裝配節拍時間大約為56 min，滿足實際生產中57 min裝配一臺臂式高空作業平臺的要求，因此整個方案可行性得到了驗證，如圖8所示。

繪制臂式高空作業平臺裝配線的工位負荷圖，可知效率和產能均得到了大幅度提升，如圖9所示。

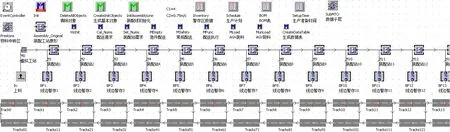
圖7 臂式高空作業平臺裝配線19個工位的完整仿真模型

圖8 仿真模型執行仿真的過程

圖9 臂式高空作業平臺裝配線工位負荷圖

3.3 配送車輛數量和速度的實驗設計

目前臂式高空作業平臺裝配線采用的配送車輛是4輛，運行速度是0.75 m/s，現在進行設計因子配比實驗設計，確定和驗證配送車輛數量和速度的最佳數量。

添加實驗管理器ExperimentManager，將標簽定義為因子設計，將輸出變量設置為EventController.SimTime，輸入變量設置為C1（配送車輛數量）和C2（車輛行駛速度），每次試驗觀察次數設置為5次，置信水平設置為95%。Tools選項，選擇兩水平試驗設計，將C1配送車輛的低水平數量為3輛，高水平數量為4輛，C2配送速度的低水平速度為0.75 m/s，高水平速度為1 m/s。

此時試驗是4次，分別為低水平C1（配送車輛為3輛）和低水平C2（配送速度為0.75m/s）、低水平C1（配送車輛為3輛）和高水平C2（配送速度為1m/s）、高水平C1（配送車輛為4輛）和低水平C2（配送速度為0.75m/s）、高水平C1（配送車輛為4輛）和高水平C2（配送速度為1 m/s）四個組合，運行仿真，試驗結果如圖10所示。

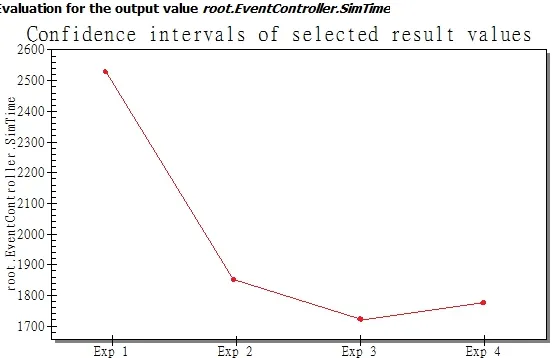
圖10 兩水平因子設計試驗結果

從試驗結果可以明顯看出試驗3是最佳方案，即高水平C1和低水平C2組合，即配送車輛為4輛，配送速度為0.75 m/s時，整個臂式高空作業平臺裝配線仿真模型達到最優效果，進一步驗證了方案的可行性。

4 結語

本文研究設計了臂式高空作業平臺裝配線，對大件物料配送采用遺傳算法進行路徑的優化求解，使用eM-plant仿真軟件對整個裝配線和物流配送進行了仿真建模，對配送車輛的數量和速度進行了實驗設計，確定了配送車輛的數量和速度的最優解，驗證了臂式高空作業平臺裝配線的物流配送系統的可行性。本文設計的臂式高空作業平臺裝配線以及物流配送系統為相關工程機械產品的裝配線設計提供參考。