協同過濾策略的異構雙種群蟻群算法*

朱宏偉，游曉明+，劉 升

1.上海工程技術大學 電子電氣工程學院，上海201620

2.上海工程技術大學 管理學院，上海201620

+通訊作者E-mail:305235598@qq.com

1 引言

在自然界中，螞蟻在發現食物后會釋放信息素用于告知其他螞蟻食物的各種信息，其他螞蟻會根據信息素的濃度等信息，選擇到達食物的最短路徑。在20世紀90年代，意大利學者Dorigo、Maniezzo等人從生物進化的機理中受到啟發，模擬自然界螞蟻尋食的行為，提出了螞蟻系統（ant system，AS）[1]，引起了專家學者的重視，并運用于商旅問題（traveling salesman problem,TSP）。實驗證明螞蟻系統取得了很好的結果。商旅問題是NP 組合優化問題中最經典的問題之一，旅行商需要從一個城市出發，不重復地遍歷所有的城市，再回到起點，形成一條閉合回路。在蟻群算法研究過程中，旅行商問題是一個很重要的檢測算法性能的基準。

雖然信息素的正反饋作用使算法更具有導向性，但也同時因為一條路徑上信息素過大而導致局部最優。1996 年，Dorigo 等人在螞蟻系統（AS）算法的基礎上提出蟻群系統（ant colony system，ACS）[2]算法，提出兩種信息素的更新方式，同時算法中加入局部搜索算法，減少了算法陷入局部最優的概率。同樣，為了限制信息素過多，Stützle等人提出了最大-最小螞蟻系統（max-min ant system，MMAS）[3]。MMAS設置一個閾值將信息素的最大值、最小值限制在其中，同時在算法進入停滯后，將信息素重新初始化，很好地改善了ACO（ant colony optimization）的不足。后來，專家學者在這兩者的基礎上不斷地改進[4-10]，文獻[4]提出一種基于禁忌搜索的蟻群算法，將禁忌搜索算法的記憶能力和藐視準則融合到蟻群算法中，使改進算法具有跳出局部最優解的能力。文獻[5]提出一種新的信息素更新策略，加強了螞蟻之間的協同作用。

實際上螞蟻是一種種群活動生物，不同的蟻群有著不一樣的信息素調控機制，這種分工組織方式使得蟻群可以完成更加復雜的任務。因此采用多種群的蟻群算法可使多個種群進行信息交換，加速收斂的速度[11-20]。文獻[11]提出將蟻群分成兩種，分別采用不同的路徑構建方式，同時固定代數進行最優解和信息素的交流，提高了解的質量。文獻[12]提出一種新的雙種群信息素擴散機制，減少算法陷入局部最優的概率。以上文獻都是將同構蟻群算法中的螞蟻進行分類，進行多種群的信息交流，而異構多種群有更優的路徑構建和保持種群多樣性的能力，如文獻[13]。

本文提出一種基于協同過濾策略的異構雙種群蟻群算法（dual population ant colony optimization，DPACO），采用MMAS 和ACS 這兩種優勢互補的異構蟻群算法相結合的策略，既保留MMAS的多樣性，同時也保留了ACS 收斂速度快的優勢，共同促進算法在大規模問題上找到最優解。引入協同過濾策略，獎勵ACS 和MMAS 中螞蟻都偏愛的路徑，以加快算法的收斂速度；當算法停滯后，根據兩個種群多樣性的動態反饋，自適應控制兩個種群交流的頻率，以保證蟻群算法發現解的廣度。算法停滯后，進行雙種群信息素的協同交互，均化每個種群不均勻的信息素，跳出局部最優。最后，引入神經網絡中失活的概念，在路徑構建時提出一種城市范圍失活的思想，減少了程序的運行時間。實驗結果表明，本文提出的異構雙種群蟻群算法比傳統的單種群蟻群算法和其他多種群蟻群算法在TSP 問題上有著更好的實驗結果，并且在大規模問題上，這種優勢更加明顯。

2 相關工作

2.1 基本蟻群算法的TSP問題

對于不同NP難問題，使用蟻群算法建立的模型設計會有所不同。本文以NP難問題中最常用的TSP問題為例說明基本蟻群算法的模型。

設螞蟻的數量為m，城市的數量為n，dij(i,j=1,2,…)代表i城市和j城市之間的距離，τij(t)代表著t時刻i城市和j城市之間的信息素的濃度大小。在ACS 和MMAS 算法中，每條邊上的起始濃度都是相同的，記為τ0。

2.2 ACS蟻群算法

2.2.1 路徑構建

ACS中每只螞蟻從i城市到j城市的選擇公式：

其中，ηij代表的是i、j城市之間距離的倒數，即q0是一定值，q是隨機數，S代表將要被選擇的下一個城市。s是另一種輪盤賭的選擇方式。公式表明，城市之間信息素高的城市和距離相對近的城市被選擇的概率更大，當q＜q0時，選用式（1），當不符合上述條件，采用輪盤賭進行路徑構建。公式如下：

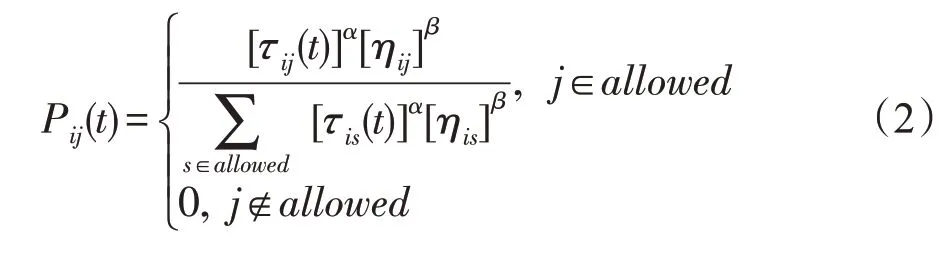
式中，allowed為螞蟻當前可行城市集。

2.2.2 信息素更新

ACS算法中分為全局信息素更新以及局部信息素更新部分。

全局信息素更新：當所有的螞蟻都完成一次周游以后，算法只允許每一代的最優螞蟻釋放信息素。全局釋放信息素主要是用于增加蟻群算法的收斂速度，使螞蟻們的選擇更具有方向性。公式為：

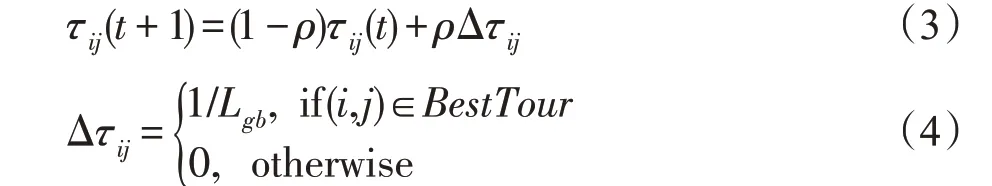
其中，ρ是全局信息素的蒸發率，Δτij是信息素增量，Lgb是當前最優路徑長度。

局部信息素更新：當所有的螞蟻都完成一次周游后，算法允許每只螞蟻都對其走過的路徑進行信息素的更新。局部信息素主要是縮小最優路徑上與非最優的信息素的差距，從而增加ACS 算法的多樣性。公式為：

式中，Δτij是信息素增量，τ0為每條邊上的起始濃度，ρ是局部信息素的蒸發率。

2.3 MMAS蟻群算法

2.3.1 MMAS算法信息素范圍限制

為了避免算法收斂過快、停滯，MMAS算法將各邊的信息素限制在一定范圍[τmin,τmax]，若τij≤τmin，則τij=τmin；若τij≥τmax，則τij=τmax,其中τmax和τmin的計算公式如式（6）和式（7）所示。

其中，Tgb是全局最優路徑。

2.3.2 MMAS算法信息素更新

當迭代完成一代時，有且僅有一只螞蟻進行信息素更新，對當前最優路徑或者全局最優路徑進行信息素更新，使最優解得到有效的利用，算法的探索能力也會增強。信息素更新規則如式（8）和式（9）：

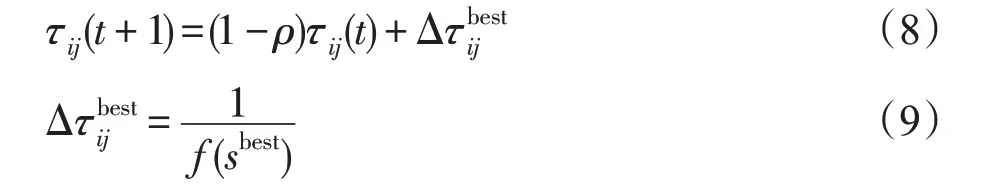
其中，f(sbest)為當前最優或者全局最優的路徑長度。

3 改進的蟻群算法

本文采用兩種目前性能較優的蟻群算法ACS和MMAS作為雙種群的兩種蟻群算法，ACS主要負責算法的收斂速度，MMAS主要負責蟻群算法的多樣性。

3.1 協同過濾策略

推薦算法是通過數學公式、算法等方式，推測出用戶更加偏好的東西，同時可以集中偏好相同的用戶。推薦算法又可以分成基于內容、基于協同、基于知識、基于效應的推薦算法。其中基于協同過濾策略的推薦算法是效果最好的。

故本文引入協同過濾策略，搜索ACS 和MMAS中最優解螞蟻都偏愛的路徑，每隔w次迭代，對該路徑進行信息素獎勵。協同的作用使算法在路徑構造時，最優解螞蟻帶動非最優螞蟻向偏愛路徑上靠攏，使算法更具有導向性；過濾的作用是去除一些相對較差的路徑，加快算法的收斂速度。協同過濾策略將兩個種群從前期到后期完全聯系在一起，不再是獨立地進行解的構建，而是形成兩個種群相互學習、共同促進的局面，使算法能以較少的迭代次數找到最優解，提高算法的性能。由于兩種算法中路徑構建的差異，在算法前期信息素濃度差距不大時，若存在偏愛路徑，說明最優解收斂在其附近的概率很大。這里僅對ACS的路徑進行信息素獎勵。這樣做有兩點原因：（1）根據文獻[3]，MMAS 對信息素的最高值設有閾值，因此對信息素的獎勵作用不敏感；（2）控制變量，僅對ACS進行信息素的獎勵，可以協調獎勵所帶來的各種影響：與沒有獎勵策略的MMAS算法進行交流，既可以照顧到獎勵所帶來快速收斂的特性，也可以彌補獎勵所帶來的負面影響。兩種算法相互制約，減少算法陷入局部最優的概率。

建立一個數學模型，通過矩陣的運算來描述本文的協同過濾策略。在T次迭代時（T是w的整數倍），為ACS 蟻群算法在T次迭代時，所有螞蟻遍歷所有城市的位置矩陣，為MMAS蟻群算法在第T次迭代時所有螞蟻的位置矩陣，如下所示。

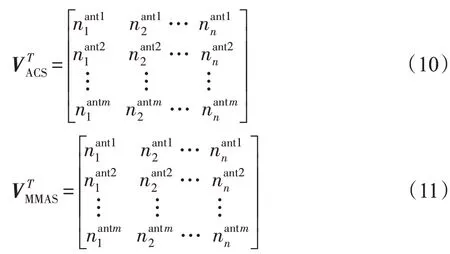
式中，n為城市的數量，m為螞蟻的個數。

設k和h分別為ACS和MMAS算法在第T次迭代中所找到最優解的螞蟻，故公共偏愛路徑為：

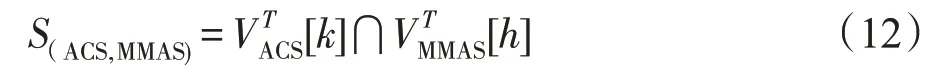
式中，S（ACS,MMAS)表示兩個種群共有的連續相同三個元素保存下來，并設為公共偏愛路徑。

3.1.1 獎勵算子

對公共偏愛路徑進行獎勵，額外的信息素獎勵因子：

式中，n為城市的數量，iter為交流時的迭代次數。故對于公共偏愛路徑部分的信息素更新為：

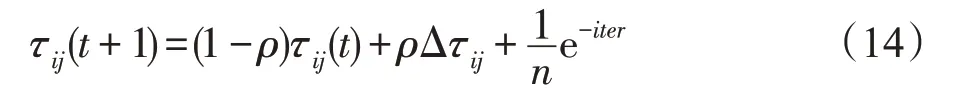
在算法前期，一條路徑被兩個種群都選到且作為當前最優路徑中的一部分，即可認為此路徑或者此路徑周圍一定存在全局最優解的組成部分。故在算法初期，獎勵的信息素較多，可以加快算法收斂速度，隨著迭代次數的增加，由式（13）可知，獎勵會越來越少，從而保證算法后期的多樣性。

3.1.2 自適應調節交流頻率

由于信息素的正反饋作用，當兩個種群信息交流過于頻繁時，過多的信息素獎勵會導致雙種群都陷入局部最優，故需要控制異構蟻群算法的交流的頻率。因此，這里通過兩個種群之間的動態反饋，自適應調整交流的次數，從而減少算法陷入局部最優的概率。設每隔w次迭代，交換概率PDPACO決定兩個種群是否進行信息交流。公式如下：

式中，T為迭代次數，k為最優解螞蟻。式（15）表示公共模式的路徑在總的路徑中比例大小。當交換概率大于等于0.5時，則表明雙種群算法的多樣性已經降低，故將不進行種群之間的交流，否則進行交流。因此，整個DPACO算法的交流頻率為：

當交流頻率過于頻繁時，獎勵作用會導致算法很快收斂到一條路徑上，造成算法多樣性下降，可能會使算法得不到滿意解；但是信息交流間隔過低時，會減弱兩個種群之間的促進作用，降低種群之間的學習效率。因此，按照式（16）自適應調整交流頻率，既可以加快算法的收斂速度，保證雙種群之間的交流與學習的機制，同時使信息素較為平穩地增長，使蟻群穩步地向最優解方向邁進，減少算法陷入局部最優的概率。

3.2 信息素的交流與均化

當兩種算法停滯后，交換ACS 和MMAS 的信息素表，從而有效地跳出局部最優。原因如下：

（1）MMAS有限制最大和最小信息素的特點，故每個城市之間信息素差距不是過于明顯，由于ACS的信息素的獎勵，導致其中幾條邊上的信息素增長速度較快，當交換了信息素表后，ACS就可以得到MMAS較為均勻的信息素，從而增加算法的種群多樣性。

（2）利用MMAS 信息素初始化的特點，可以將ACS 上的邊的不均勻的信息素重新初始化，有利于算法跳出局部最優。

在蟻群算法的中后期，信息素的濃度在路徑構建中所在的權重不斷增大，因此本文提出的信息素交換方式不斷均化和調節兩個種群之間的信息素，使算法跳出局部最優的能力更強。與典型的跳出局部最優的方式相比（如MMAS，當算法停滯時，將所有信息素重新初始化），本文提出種群間信息素的交換既將信息素回歸到一個合理的范圍，增加了蟻群的多樣性，同時也保留了算法在前期所積累的經驗，增加算法的收斂速度，而MMAS 蟻群算法的信息素重新初始化，就會否定所有的先前經驗。故信息素的交流和均化很好地平衡了蟻群算法的多樣性和收斂性。

3.3 城市的范圍失活

失活的思想最先被提出在神經網絡中。隨機失活的目的是減少神經網絡由于節點過多而產生的大量計算，以及造成網絡的過擬合作用。過擬合與陷入局部最優的概念相類似，故本文將失活的思想引入蟻群算法中。針對城市規模大造成的計算過多、較慢的問題，本文提出一種城市范圍失活的方法，與可訪問城市表（Allowed）相結合，使得算法每次迭代中每只螞蟻的計算城市的數目都會大量減少。如圖1，中心點為螞蟻正處于的城市，以這個城市的中心畫一個半徑為r的圓，會將Allowed城市表中的城市分成兩種：一種在圓的范圍中，一種在圓的范圍外。將圓范圍外的城市失活，即不再計算它們的轉移概率，這樣很大程度上減少了每次計算的城市的數目。由于本文所選TSP城市數目較多而緊密，同時給出半徑相對較大，蟻群在路徑構建時，即使計算了半徑外的節點，最終也不會選擇其作為下一城市，故城市范圍失活的方法不會影響算法的構造解的精度，卻可以極大地減少程序的運行時間。半徑r的大小的選擇：

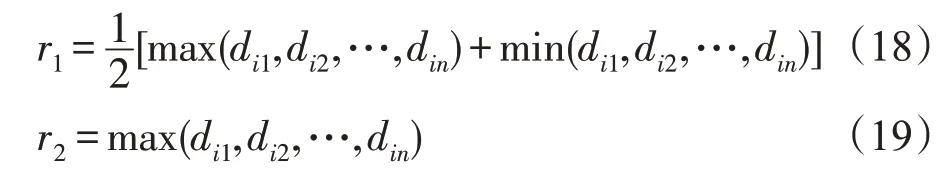
式中，i為螞蟻當前所在的城市，din表示第i和第n城市之間的距離。當使用r1半徑大小的圓與Allowed城市表相結合而沒有可選點時，使用r2的半徑大小。

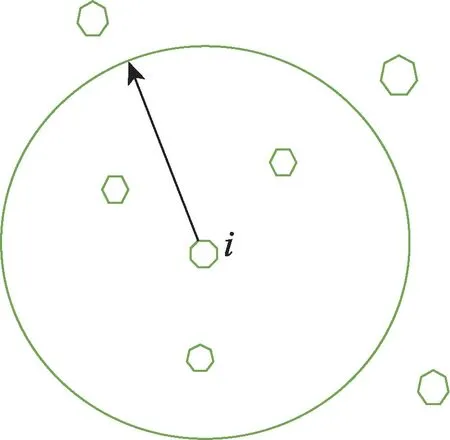
Fig.1 Current city and other cities圖1 當前城市與其他城市

3.4 算法流程

DPACO algorithm for TSP

3.5 時間復雜度

從上述算法流程的分析可以看出，兩個種群是并行實現的，因此DPACO 的時間復雜度為O((m1×(n-1)+m2×(n-1))×R)，式中m1為MMAS 算法中螞蟻的數量，m2為ACS 算法中螞蟻的數量，R為最大迭代次數。設所有螞蟻的總數為m，故DPACO的最大時間復雜度為O(m×n×R)，MMAS 的最大時間復雜度為O(m×n×R)，ACS最大時間復雜度為O(m×n×R)。由此看出，本文提出的DPACO蟻群算法沒有改變算法的最大復雜度。

4 實驗仿真

本實驗在Matlab R2014a 的環境下仿真運行，為了檢測改進算法的有效性，以及顯示本文算法在解決中大規模TSP 問題上的優勢，選取Eil76、ch130、KroB150、KroA200、KroB200、lin318 等中大規模TSP算例來進行算法的驗證。與經典單種群ACS、MMAS算法以及其他多種群蟻群算法進行數據對比，每種算法都進行15 次仿真實驗，不同的測試集螞蟻的數量、啟發式的值等會有所調整。DPACO 在各個測試集中的參數設置如表1所示。

4.1 節展示了DPACO、ACS、MMAS 3 種蟻群算法的性能分析和對比，以及獎勵算子對信息素分布的影響。實驗表明DPACO 無論是收斂速度還是最優解都優于其他兩種算法，在前期DPACO可以快速地收斂，算法后期可以跳出局部最優，提高解的質量。

4.2 節展示了DPACO 算法與其他多種群蟻群算法之間的對比實驗，算法實驗數據皆來自于其相應論文，實驗表明，本文提出的改進算法的最優解要優于其他3種雙種群蟻群算法。

4.3 節展示了城市范圍失活方法對仿真實驗的時間的影響。實驗表明城市范圍失活方法可以大量減少程序的運行時間。同時增加了對比實驗，驗證了本文所選的失活半徑具有較好的特性。

4.4 節展示了DPACO 所找到的最優解以及與ACS、MMAS的迭代對比圖。

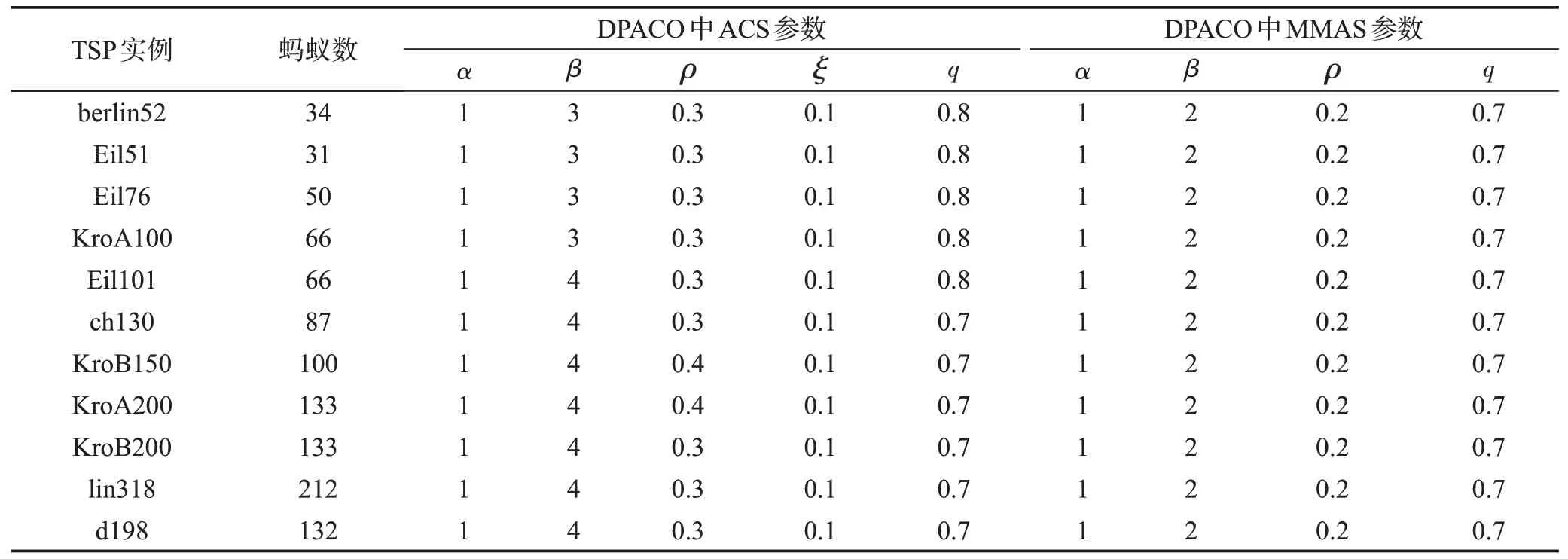
Table 1 Parameters setting in each test set of DPACO表1 DPACO在各個測試集中的參數設置

4.1 不同TSP問題求解與比較

為了對比MMAS、ACS 和DPACO 的算法性能，本文選取Eil76、ch130、KroB150、KroA200、KroB200、lin318等中大規模TSP算例來進行分析，同時從最優解、平均解、誤差率J、收斂速度等幾個方向進行實驗分析，如表2 所示。使用式（20）衡量每種ACO 與測試集最優解之間的差距，即誤差率，公式如下：

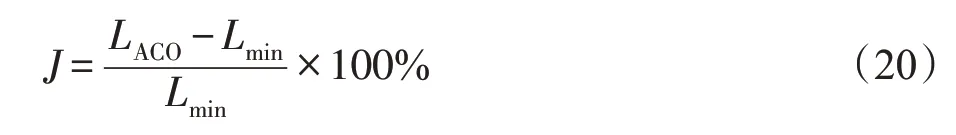
式中,LACO為3 種ACO 算法所找到的最優解,Lmin為測試集的最優解。

從表2 結果可以看出，DPACO 在所有規模測試集中，無論是最優解、平均解，還是誤差率等方面都優于ACS 和MMAS。同時從最終迭代數分析，DPACO在中小規模測試集上由于兩個種群信息的交換以及其獎勵策略，其收斂速度相對于其他ACO 算法速度最快；對于大規模測試集問題，由于最優解較難尋找，所有蟻群算法皆易陷入局部最優，本文提出的DPACO算法在沒有找到最優解時，兩個種群就會一直進行信息交流，算法在前期很快收斂到最優解附近。同時，在算法陷入局部最優后，由于控制雙種群交流頻率和信息素的交換，使得DPACO中兩個種群的信息素的值都被限制，增加了跳出局部最優的概率，故算法總可以找到最優解。

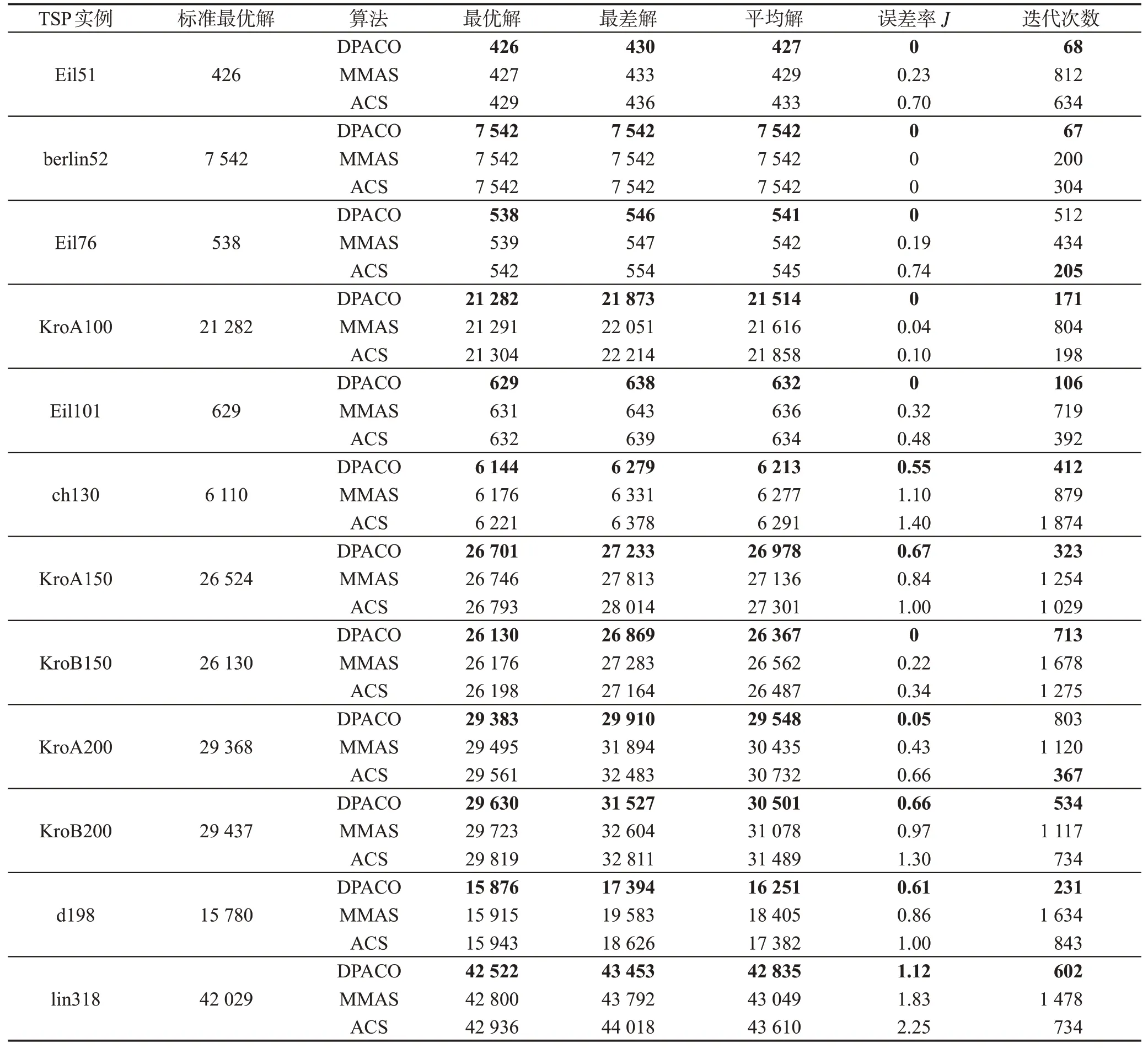
Table 2 Performance comparison of DPACO,MMAS,ACS in different test sets表2 DPACO、MMAS、ACS在不同測試集的性能對比

3.1 節提出僅對ACS信息素更新部分進行獎勵，下面舉例分析獎勵算子對信息素濃度的影響。圖2和圖3為在KroA200測試集中，雙種群中每個種群在算法停滯前信息素濃度與城市之間的關系。X軸和Y軸代表城市，Z軸代表信息素濃度。從圖2可以看出，MMAS 蟻群算法中每個城市之間信息素濃度差距不大，僅對ACS 的偏愛路徑進行獎勵，是由于MMAS限制了信息素濃度的最大最小值，故對MMAS進行信息素獎勵效果一般。

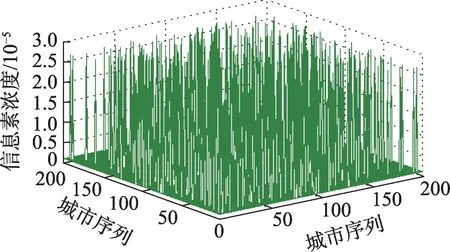
Fig.2 MMAS pheromone圖2 MMAS信息素濃度

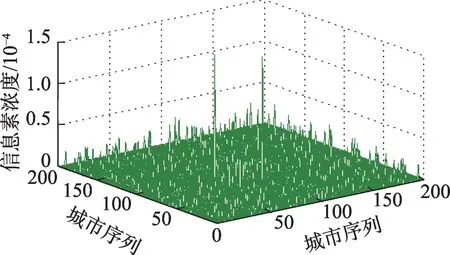
Fig.3 ACS pheromone with reward圖3 帶有獎勵的ACS信息素濃度

圖3 為ACS 的信息素濃度，由于獎勵的作用，導致幾個城市之間信息素濃度增加較為明顯。在蟻群算法前期，信息素的權重對路徑構建產生的影響相對較小，若兩個種群卻產生了偏愛路徑，故該路徑有很高的概率為全局最優解組成部分，獎勵該路徑增強了算法在前期的收斂速度，使算法快速收斂到最優解附近。

同時本文在3.2 節提出，當算法停滯時，交換雙種群信息素濃度表，以達到跳出局部最優的目的。從圖2 和圖3 可以看出，交換后，ACS 會得到MMAS的相對均勻的信息素濃度表，同時MMAS 也會將ACS的信息素濃度重置，并且均勻化。

4.2 與其他多種群蟻群算法的對比

本文改進算法還與其他異構多種群蟻群算法進行比較。其中文獻[13]提出一種多交流策略的雙種群算法（heuristic communication heterogeneous dual population ant colony optimization，HHACO）；文獻[14]提出基于優勝劣汰規則的異類多種群蟻群算法（heterogeneous multiple ant colony algorithm based on survival of fittest rules，HMACSF）；文獻[15]提出基于相似度的自適應異類多種群蟻群（adaptive heterogeneous multiple ant colonies algorithm based on similarity，AHMACAS）。表3中的數據皆來自于上述文獻。實驗結果顯示，在Eil51和Eil76測試集上，本文DPACO算法的精度要優于其他3種算法；在KroA100測試集上雖然4種算法都找到了測試集最優解，但是本文算法的收斂速度要更快。

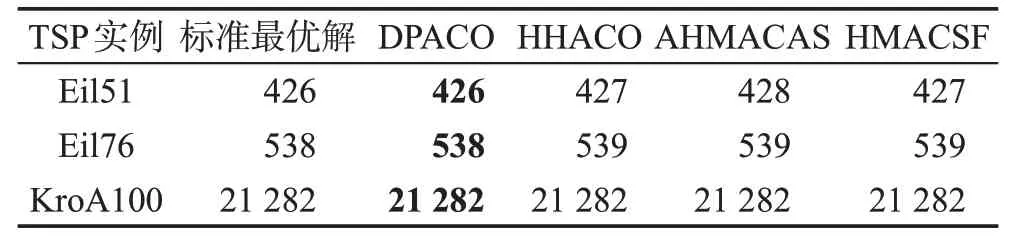
Table 3 Comparison of DPACO with other algorithms表3 DPACO與其他多種群的對比

根據4.1節和4.2節的實驗結果，可以得出DPACO算法優于其他蟻群算法。與單種群相比，提升了解的質量，增加了算法的多樣性，使算法收斂速度更快；跟多種群相比，DPACO算法提高了解的精度。

4.3 城市失活策略

4.3.1 城市范圍失活的時間對比

本文提出的城市范圍失活方法，在大規模問題上可以非常明顯地減少整個程序的運行時間，即程序完成迭代次數所花費的總時間。本文設置一個對比實驗，對于DPACO 蟻群算法，使用城市范圍失活的方法，這里稱為DPACO-1；不使用失活的方法，稱為DPACO-2。表4 為DPACO-1 和DPACO-2 運行到最大迭代次數在不同測試集的時間差。

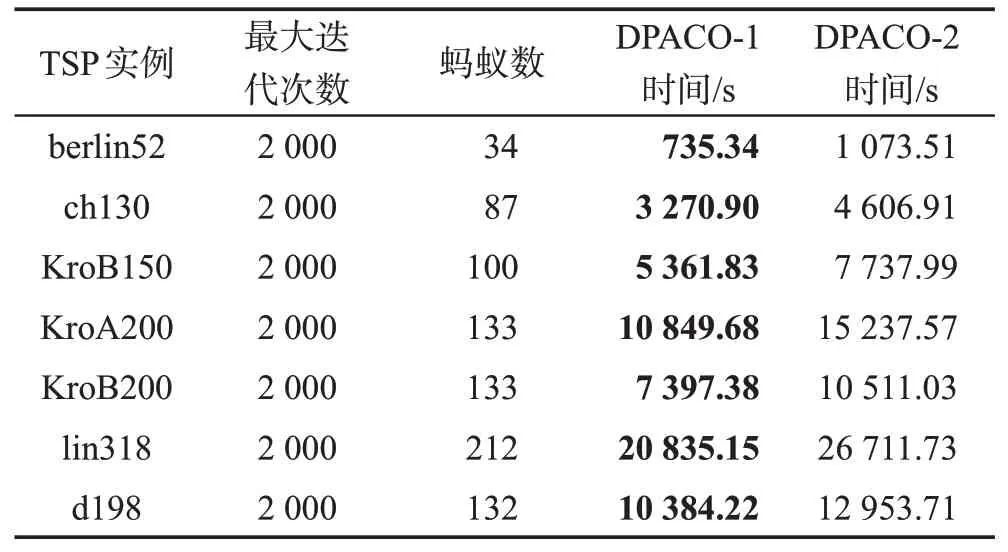
Table 4 Time comparison表4 時間對比

由表4 可知，隨著測試集中城市數量的增加，運行時間是增加的；在同一測試集中，由于范圍失活算法所帶來的計算城市數目的減少，DPACO-1的運行時間要明顯少于DPACO-2。設時間比t′=tDPACO-1/tDPACO-2，通過表4中數據計算，發現在大多數測試集中時間比一直在[0.67,0.71]之間浮動，且隨著城市數目增加，時間比呈現略微增長趨勢。這些測試集中的城市分布較均勻，但是在d198 和lin318 測試集中，時間比t卻增加明顯，這與測試集規模大小、城市之間密集程度有關。這兩個測試集城市分布十分密集，范圍失活的城市數量比較有限，故造成時間比增加。圖4為不同測試集的時間比對比圖。

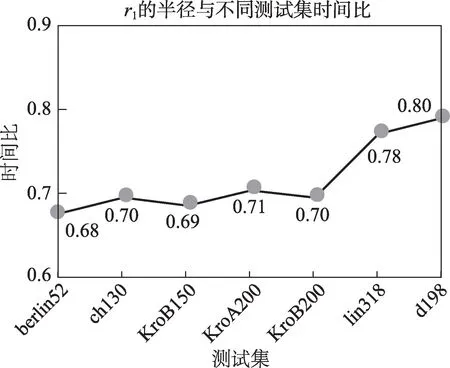
Fig.4 Time ratio trend for different test sets圖4 不同測試集的時間比趨勢

4.3.2 不同的失活判定標準的影響

為了驗證不同的判定標準對時間比和最優解的影響，本文設置了幾組不同的判定標準與本文標準r1（式（18））進行對比。同時當范圍內沒有城市可以選時，都選擇r2的半徑大小（式（19））。對比實驗半徑如下：

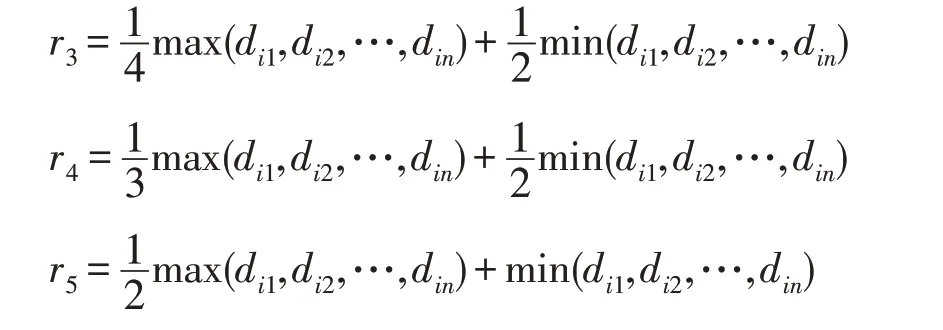
這些判定標準中，半徑大小為r3＜r4＜r1＜r5，不同的r在不同測試集中對時間比的影響如圖5所示。

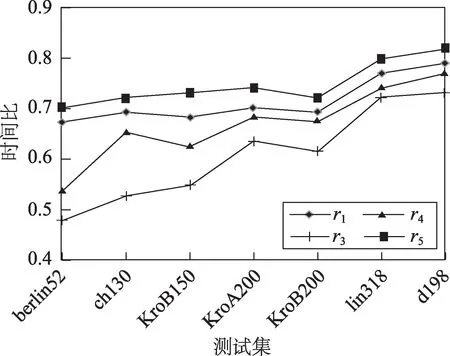
Fig.5 Influence of different judgments on time ratio of test set圖5 不同判定標準對測試集時間比影響

由圖5可以看出，不同的判定標準在各種測試集中時間比為t3＜t4＜t1＜t5。當半徑不斷縮小時，失活的城市會越來越多，會減少大量計算，導致時間比進一步減少，即程序運行時間變短。相反，當半徑變大時，時間比會相應增加。故在縮短程序運行時間方面，以r3和r4的半徑大小會使程序運行時間更短。但是當以r3和r4的半徑值時，會使算法找到最優解有所下降，這是由于當失活半徑過小時，部分測試集中城市分布較為松散，如berlin52、d198等，會造成最優城市的丟失。而r1和更大半徑r5把最優城市以及其周邊城市都包在其中，故蟻群所找到最優解幾乎沒有多大差別。表5 為部分測試集中4 種失活半徑所找到的最優解。

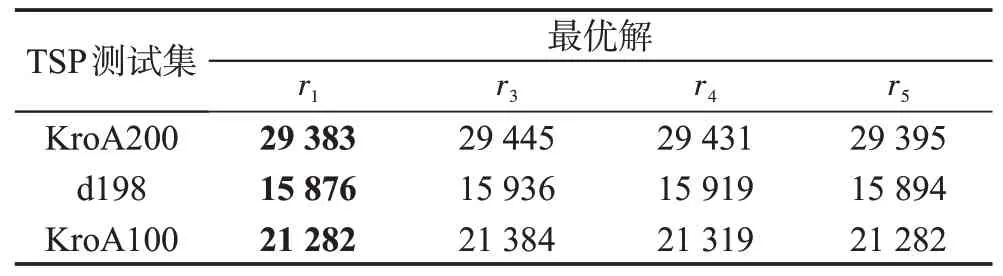
Table 5 Influence of different radii on optimal solution表5 不同半徑大小對最優解影響

4.4 DPACO最優解與收斂速度對比

圖6～圖15 為DPACO 的最優解，以及與ACS 和MMAS 的收斂速度對比。由圖6～圖15 可以看出，DPACO在前期保留了比ACS更快的收斂速度，使解快速收斂到最優解附近；同時在后期算法停滯時，本文算法由于采用信息素交換和控制交流的頻率等策略，易跳出局部最優，提高解的精度，從而實驗結果比單種群ACS和MMAS更好。

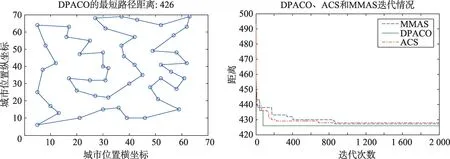
Fig.6 Eil51 test set圖6 Eil51測試集

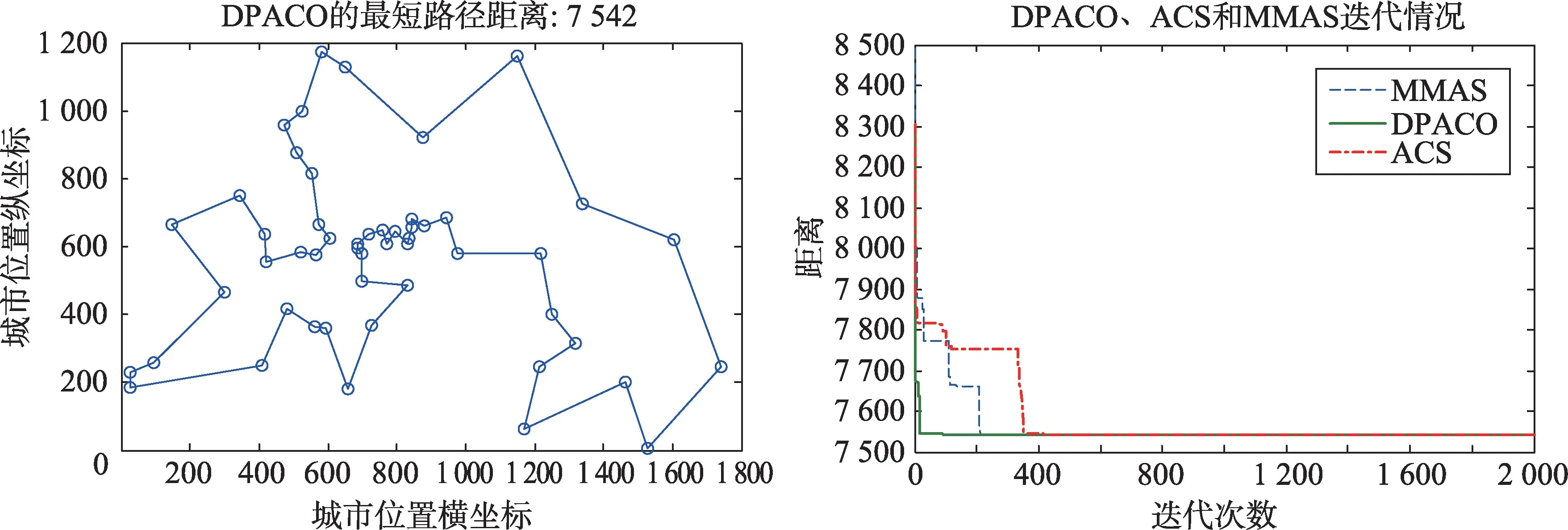
Fig.7 berlin52 test set圖7 berlin52測試集

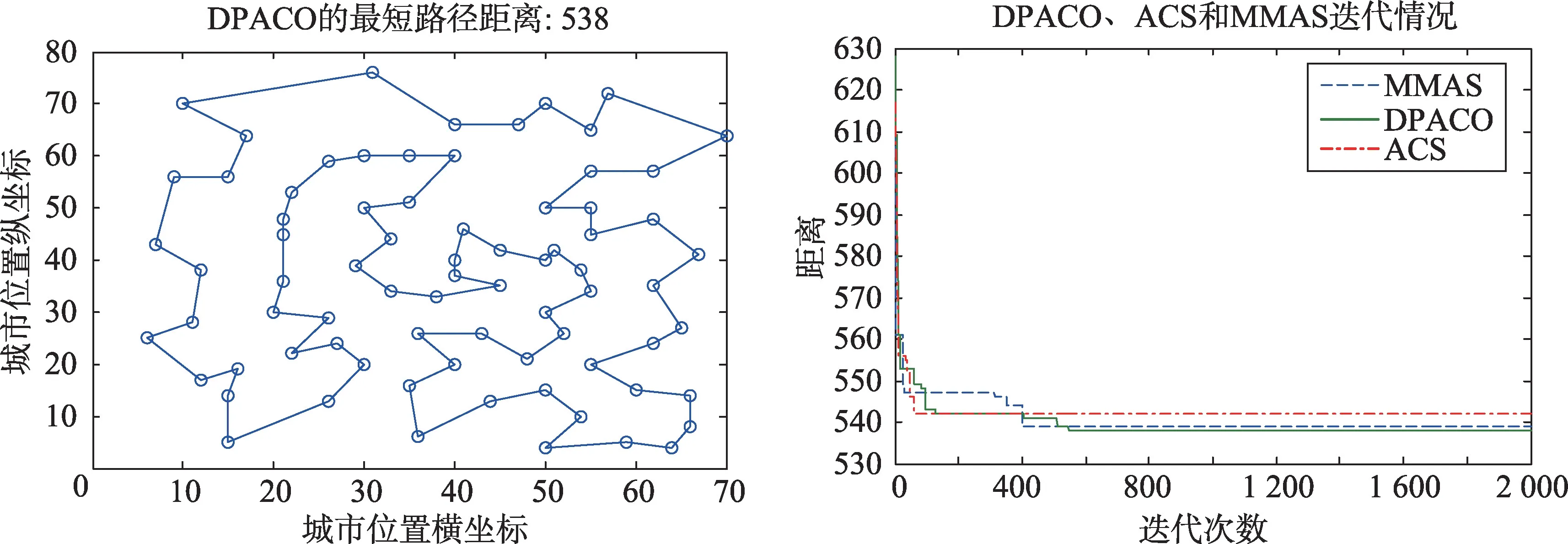
Fig.8 Eil76 test set圖8 Eil76測試集

Fig.9 KroA100 test set圖9 KroA100測試集

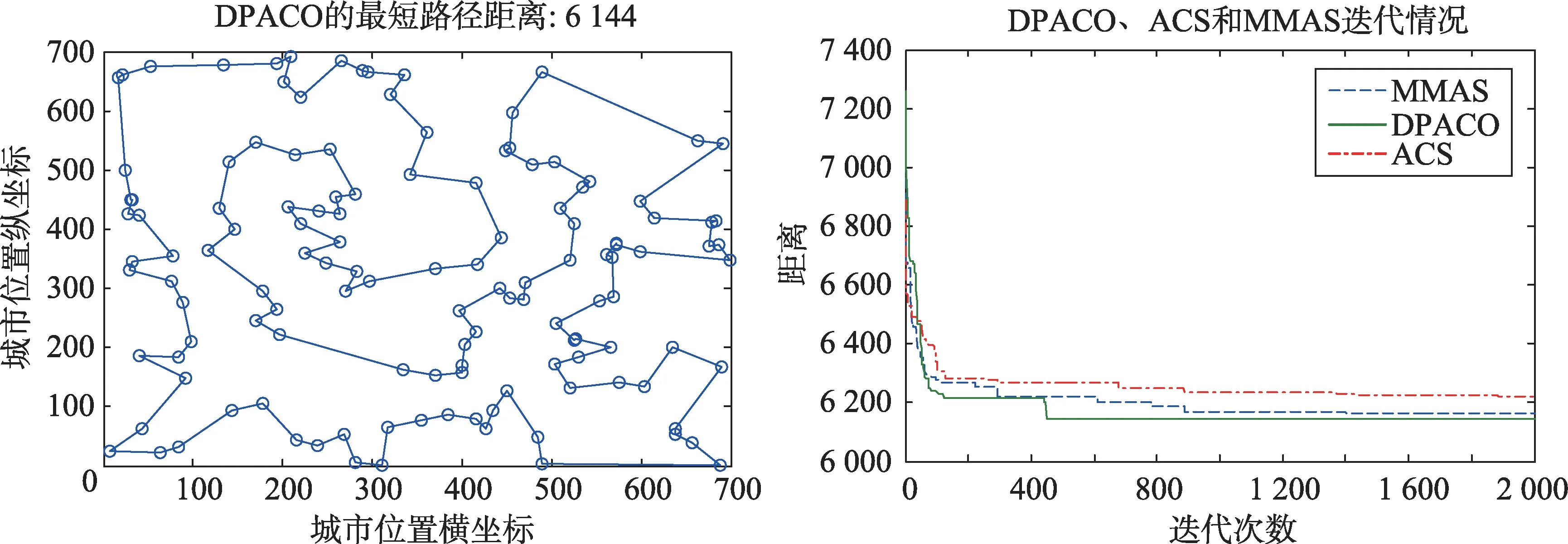
Fig.10 ch130 test set圖10 ch130測試集

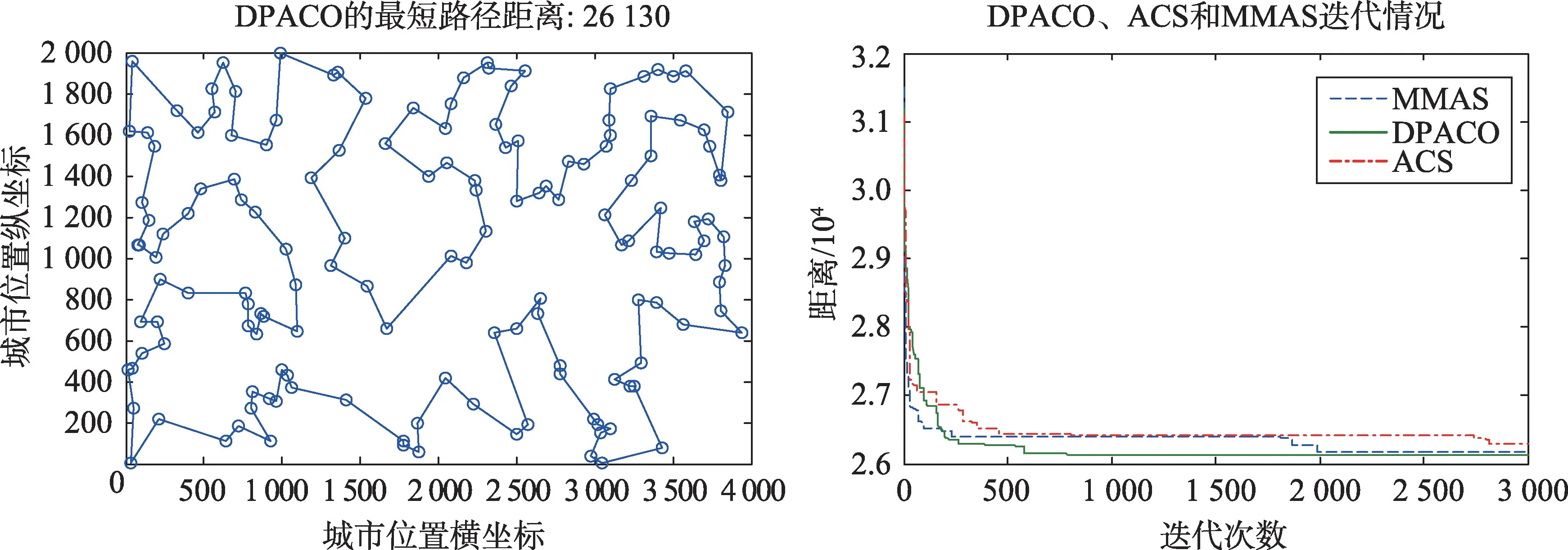
Fig.11 KroB150 test set圖11 KroB150測試集

5 結束語

本文提出了一種使用ACS 和MMAS 作為兩個種群，引入協同過濾的思想，獎勵雙種群中螞蟻都偏愛的路徑，提高了解的質量，同時自適應調整雙種群的交流頻率，減少算法陷入局部最優的概率。算法的后期，當雙種群算法停滯后，雙種群信息素協同交流，應用MMAS信息素初始化和設定的閾值等特點，極大增強了算法跳出局部最優的能力。在路徑構造階段每個種群都使用城市范圍失活的方法，使整個程序的運行時間大大減少。雖然本文算法在所有規模測試集中，解的質量提升較多，且中小規模測試集中收斂速度提升明顯，但對于大規模TSP問題上，算法后期收斂速度較慢，為此下一步繼續優化多種群蟻群算法的獎勵算子，以加快算法在大規模問題上的收斂速度。

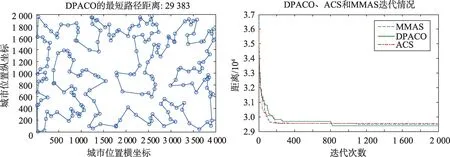
Fig.12 KroA200 test set圖12 KroA200測試集

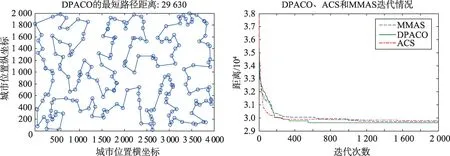
Fig.13 KroB200 test set圖13 KroB200測試集

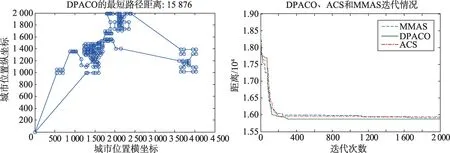
Fig.14 d198 test set圖14 d198測試集

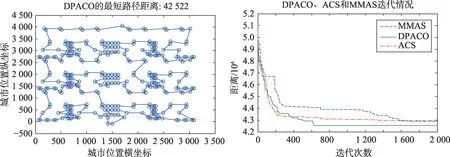
Fig.15 lin318 test set圖15 lin318測試集