解決兩類立體幾何難題的新方法

朱小扣 藍(lán)云波

(1.安徽省無(wú)為第三中學(xué)城北校區(qū) 238351;2.廣東省興寧市第一中學(xué) 514500)

《普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)(2017版)》中指出：“數(shù)學(xué)學(xué)科核心素養(yǎng)包括：數(shù)學(xué)抽象，邏輯推理，數(shù)學(xué)建模，直觀想象，運(yùn)算能力，數(shù)據(jù)分析，這些核心素養(yǎng)既相對(duì)獨(dú)立又相互交融，是一個(gè)有機(jī)的整體.”而高考的命題勢(shì)必會(huì)考查這些核心素養(yǎng)，這就對(duì)學(xué)生的空間想象能力，化歸能力等能力提出了更高的要求，所以有時(shí)在高考立體幾何中取得高分非常不容易，有時(shí)必須要另辟蹊徑.本文將用兩個(gè)新的方法來解決此類問題，以期拋磚引玉.

一、利用標(biāo)數(shù)法破解三視圖問題

對(duì)三視圖的考查一直是高中數(shù)學(xué)的重點(diǎn)，往往是通過三視圖還原物體的直觀圖，從而計(jì)算直觀圖的表面積和體積.但還原物體的直觀圖卻是學(xué)生學(xué)習(xí)和教師教學(xué)的難點(diǎn).不少老師在講解時(shí)往往在課件上用不同顏色區(qū)分不同的視圖所表示的點(diǎn)，筆者覺得這樣去教農(nóng)村的考生而言并不好操作(條件差)，并且在考試時(shí)用不同的顏色畫點(diǎn)線，重合時(shí)也有干擾.為此筆者創(chuàng)造出了“標(biāo)數(shù)法”，舉例如下，供大家參考.

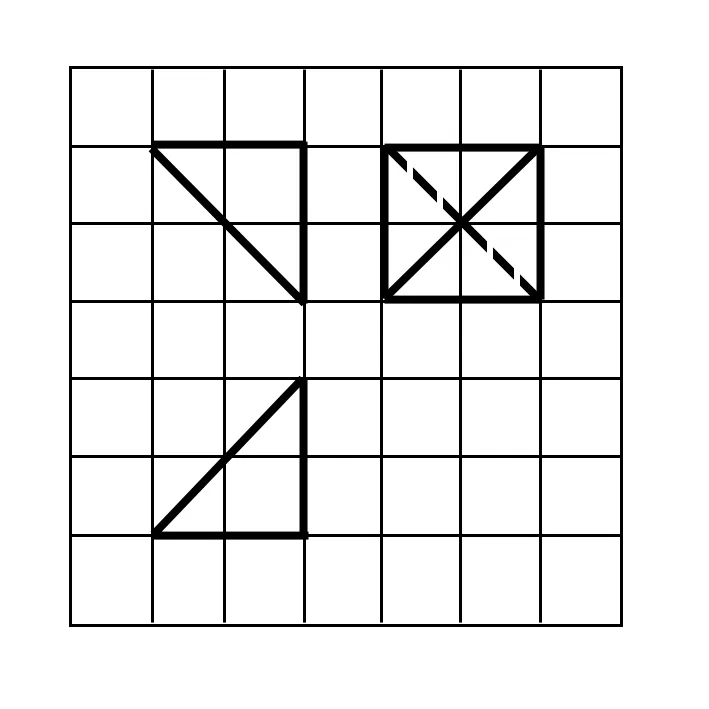
例1 (2016年河北省邯鄲一模)如圖，網(wǎng)格紙上小正方形的邊長(zhǎng)為1，粗線畫出的是某四面體的三視圖，則該四面體的表面積為( ).

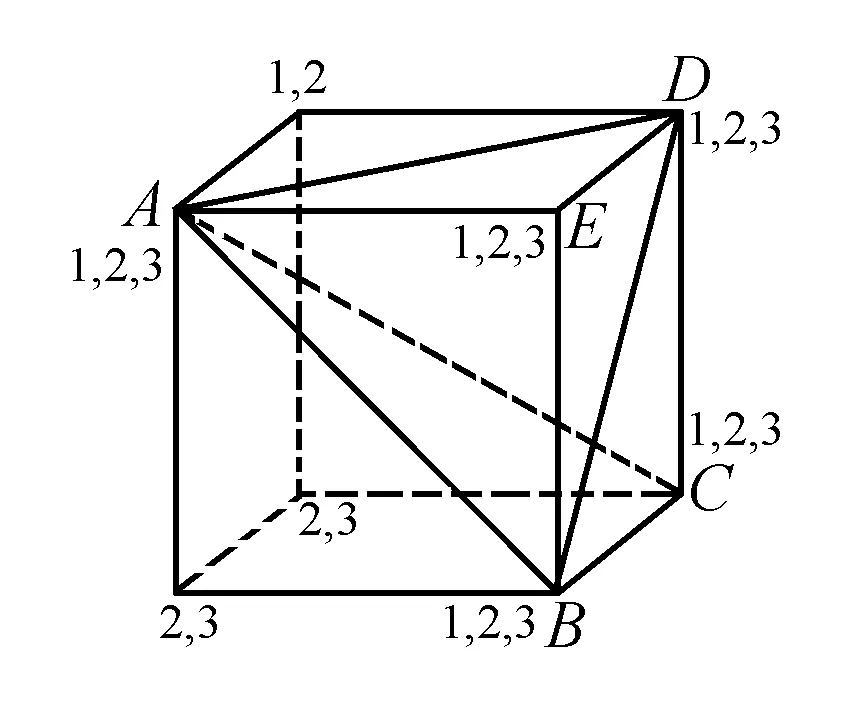
圖1

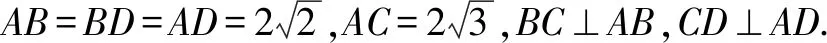
上題如不用標(biāo)數(shù)法，極容易出錯(cuò).又如：

例2 (2016年安徽省蚌埠一模)某空間幾何體的三視圖如圖所示，則該幾何體的體積為( ).

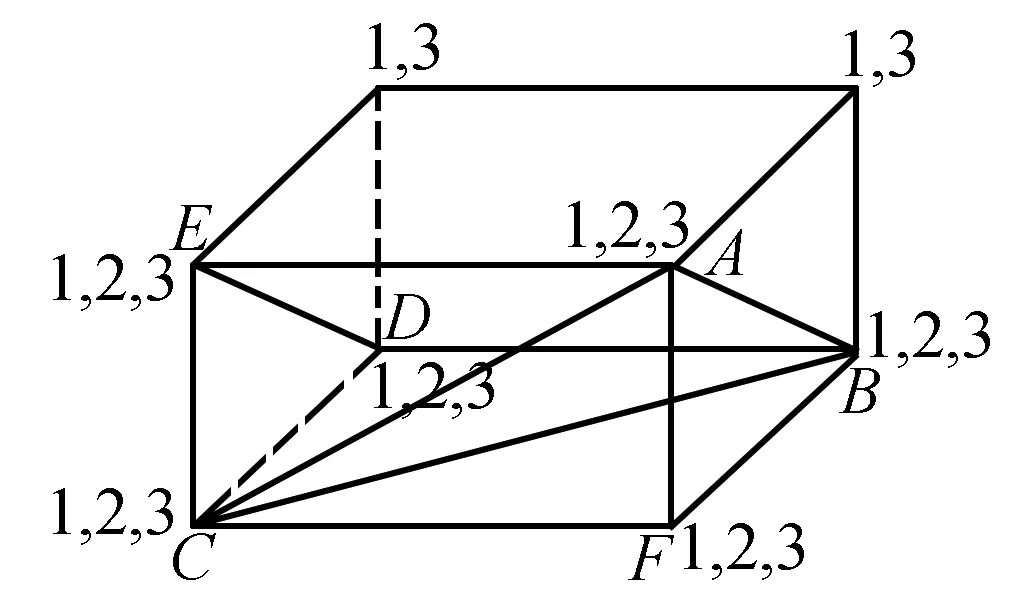
圖2

解析如圖2，利用正視圖，在可能的長(zhǎng)方體的頂點(diǎn)上標(biāo)上“1”；利用側(cè)視圖，在可能的長(zhǎng)方體的頂點(diǎn)上標(biāo)上“2”；再利用俯視圖，在可能的長(zhǎng)方體的頂點(diǎn)上標(biāo)上“3”，得到了同時(shí)擁有“1，2,3”的6個(gè)點(diǎn)A,B,C,D,E，F(xiàn)，再經(jīng)過確認(rèn)排除點(diǎn)F，于是得到所求幾何體是多面體ABCDE：

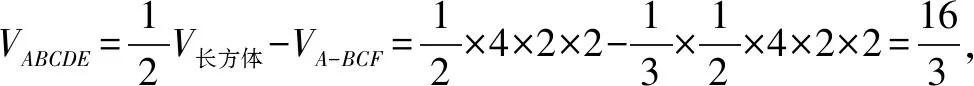
點(diǎn)評(píng)在近幾年的各類考試中，以三視圖為背景的試題屢見不鮮，且常考常新，應(yīng)引起高度的重視，但由于學(xué)生空間想象力的匱乏，無(wú)法迅速地還原出直觀圖，導(dǎo)致考試丟分.這同樣給教師的教學(xué)帶來麻煩.但如果利用標(biāo)數(shù)法，標(biāo)上“1”“2”“3”，就可以三位一體，使得問題迅速地，正確地解決.

二、三面角余弦定理破解二面角問題

在做二面角題時(shí)，有時(shí)不能用常規(guī)的方法(如找角法，垂面法，向量法等)來解決時(shí)，這時(shí)我們可以想想還可用三面角的余弦定理，三面角的余弦定理如下：

1.三面角余弦定理

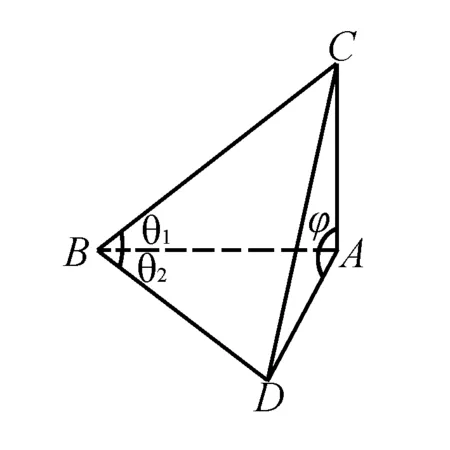
圖3

2.三面角定理的應(yīng)用

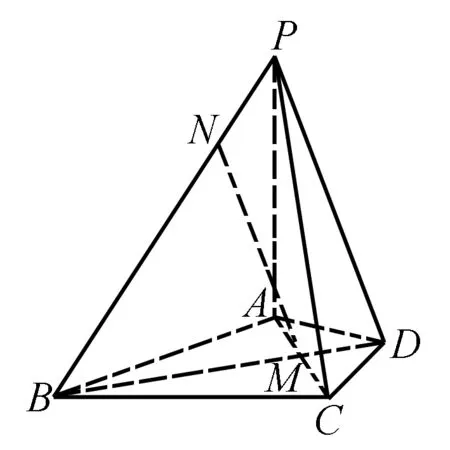
圖4

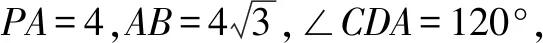
(1)求證：BD⊥PC；

(2)求證：MN∥平面PDC；

(3)求二面角A-PC-B的余弦值.

解析(1)(2)(略).

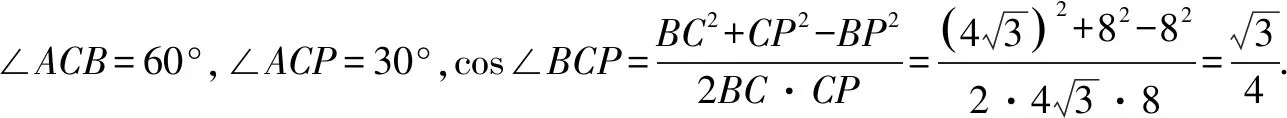
故由三面角的余弦定理定理得：

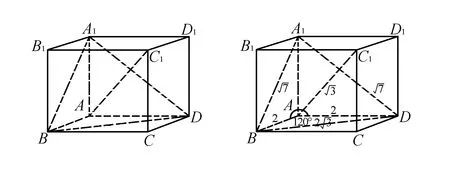
圖5 圖6

(1)求異面直線A1B與AC1所成角的余弦值；

(2)求二面角B-A1D-A的正弦值.

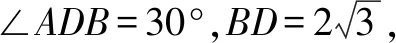
點(diǎn)評(píng)通過三面角的余弦定理，可以迅速地解決二面角問題，也可以彌補(bǔ)學(xué)生空間想象能力的不足.需要注意的是,三個(gè)角的位置不能搞混亂，才開始寫的時(shí)候可以用圖3“照葫蘆畫瓢”，多寫幾次就能熟練地掌握.

總結(jié)高考是選拔人才的考試，想取得高分，僅僅對(duì)知識(shí)達(dá)到初步的理解和掌握還是不行的，必須加以延拓并靈活運(yùn)用.可能有的老師對(duì)介紹本文的“超綱”知識(shí)，并不認(rèn)同，但正如不管是發(fā)現(xiàn)法教學(xué)，還是探究法，拋錨法，范例法等方法來教學(xué)，如果僅僅依靠某一種或幾種教學(xué)方法，就能達(dá)到學(xué)生能力的提高，我覺得也是“教條主義”.教無(wú)定法，學(xué)無(wú)定法，解題亦無(wú)定法.